Глава 23 РЕЗОНАНС

Глава 23

РЕЗОНАНС

§ 1. Комплексные числа и гармоническое движение

§ 2. Вынужденные колебания с торможением

§ 3. Электрический резонанс

§ 4. Резонанс в природе

§ 1. Комплексные числа и гармоническое движение

Мы снова будем говорить в этой главе о гармоническом осцилляторе, особенно об осцилляторе, на который действует внешняя сила. Для анализа этих задач нужно развить новую технику. В предыдущей главе мы ввели понятие комплексного числа, которое состоит из действительной и мнимой частей и которое можно изобразить на графике. Действительная часть числа будет изображаться абсциссой, а мнимая — ординатой. Комплексное число а можно записать в виде a=a_r+ia_i; при такой записи индекс r отмечает действительную часть а, а индекс i — мнимую. Взглянув на фиг. 23.1, легко сообразить, что комплексное число a=x+iy можно записать и так: x+iy=rexp(iq), где r²=x²+y²=(x+iy)(x-iy)=aa * (а* — это комплексно сопряженное к а число; оно получается из а изменением знака i).

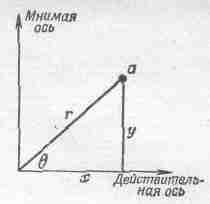
Фиг. 23,1. Комплексное число, изображенное точкой на «комплексной плоскости».

Итак, комплексное число можно представить двумя способами: явно выделить его действительную и мнимую части или задать его модулем rи фазовым углом q. Если заданы r и q, то х и у равны rcosq и rsinq, и, наоборот, исходя из числа x+iy, можно найти r=Ц(x²+y²)и угол q; tgq равен у/х (т. е. отношению мнимой и действительной частей).

Чтобы применить комплексные числа к решению физических задач, проделаем такой трюк. Когда мы изучали осциллятор, то имели дело с внешней силой, пропорциональной coswt. Такую силу F=F₀coswt можно рассматривать как действительную часть комплексного числа F = F₀exp(iwt), потому что exp(iwt)=coswt+isinwt. Такой переход удобен: ведь иметь дело с экспонентой легче, чем с косинусом. Итак, трюк состоит в том, что все относящиеся к осциллятору функции рассматриваются как действительные части каких-то комплексных функций. Найденное нами комплексное число F, разумеется, не настоящая сила, ибо физика не знает комплексных сил: все силы имеют только действительную часть, а мнимой части взяться просто неоткуда. Тем не менее мы будем говорить «сила» F₀exp(iwt), хотя надо помнить, что речь идет лишь о действительной ее части.

Рассмотрим еще один пример. Как представить косинусоидальную волну, фаза которой сдвинулась на D? Конечно, как действительную часть F₀exp[i((wt-D₂)]; экспоненту в этом случае можно записать в виде exp[i(wt-D)]=ехр(iwt)exp(^-iD). Алгебра экспонент гораздо легче алгебры синусов и косинусов; вот почему удобно использовать комплексные числа. Часто мы будем писать так:

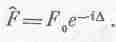
Шляпка над буквой будет указывать, что мы имеем дело с комплексным числом, т. е.

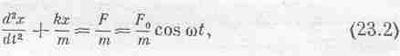
Однако пора начать решать уравнения, используя комплексные числа, тогда мы увидим, как надо применять комплексные числа в реальных обстоятельствах. Для начала попытаемся решить уравнение

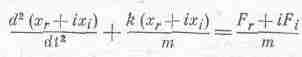
где F — действующая на осциллятор сила, а х — его смещение. Хотя это и абсурдно, предположим, что х и F — комплексные числа. Тогда х состоит из действительной части и умноженной на i мнимой части; то же самое касается и F. Уравнение (23.2) в этом случае означает

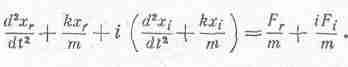
или

Комплексные числа равны, когда равны их действительные и мнимые части; следовательно, действительная, часть х удовлетворяет уравнению, в правой части которого стоит действительная часть силы. Оговорим с самого начала, что такое разделение действительных и мнимых частей возможно не всегда, а только в случае линейных уравнений, т. е. уравнений, содержащих х лишь в нулевой и первой степенях. Например, если бы уравнение содержало член lх², то, сделав подстановку x_r+ix_t, мы получили бы l(x_r+ix_i)², и выделение действительной и мнимой частей привело бы нас к l(х²_r-x²_i) и 2ilx_rx_i. Итак, мы видим, что действительная часть уравнения содержит в этом случае член -lx²_i. Мы получили совсем не то уравнение, какое собирались решать.

Попытаемся применить наш метод к уже решенной задаче о вынужденных колебаниях осциллятора, т. е. об осцилляторе, на который действует внешняя сила. Как и раньше, мы хотим решить уравнение (23.2), но давайте начнем с уравнения

где 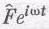— комплексное число. Конечно, х — тоже комплексное число, но запомним правило: чтобы найти интересующие нас величины, надо взять действительную часть х. Найдем решение (23.3), описывающее вынужденные колебания. О других решениях поговорим потом. Это решение имеет ту же частоту, что и внешняя (приложенная) сила. Колебание, кроме того, характеризуется амплитудой и фазой, поэтому если представить смещение числом , то модуль его скажет нам о размахе колебаний, а фаза комплексного числа — о временной задержке колебания. Воспользуемся теперь замечательным свойством экспоненты:

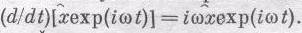
Дифференцируя экспоненциальную функцию, мы опускаем вниз экспоненту, делая ее простым множителем. Дифференцируя еще раз, мы снова приписываем такой же множитель, поэтому очень просто написать уравнение для 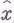: каждое дифференцирование по времени надо заменить умножением на iw. (Дифференцирование становится теперь столь же простым, как и умножение! Идея использовать экспоненциальные функции в линейных дифференциальных уравнениях почти столь же грандиозна, как изобретение логарифмов, которые заменили умножение сложением. Здесь дифференцирование заменяется умножением.) Таким образом, мы получаем уравнение

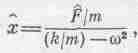
[Мы опустили общий множитель eⁱ^w^t.]Смотрите, как все просто! Дифференциальное уравнение немедленно сводится к чисто алгебраическому; сразу же можно написать его решение

поскольку (iw)²=-w². Решение можно несколько упростить, подставив k/m=w²₀, тогда

Это, конечно, то же самое решение, которое уже было нами получено ранее. Поскольку m(w²₀-w²) — действительное число, то фазовые углы F и х совпадают (или отличаются на 180°, если (w²>w²₀). Об этом тоже уже говорилось. Модуль х, который определяет размах колебаний, связан с модулем F множителем 1/m(w²₀-w²); этот множитель становится очень большим, если w приближается к w₀. Таким образом, можно достичь очень сильного отклика, если приложить к осциллографу нужную частоту w (если с нужной частотой толкать подвешенный на веревочке маятник, то он поднимается очень высоко).

§ 2. Вынужденные колебания с торможением

Итак, мы можем решить задачу о колебательном движении, пользуясь изящной математикой. Однако изящество немногого стоит, когда задача и так решается просто; математику надо использовать тогда, когда решаются более сложные задачи. Перейдем поэтому к одной из таких задач, которая, кроме того, ближе к действительности, чем предыдущая. Из уравнения (23.5) следует, что, если w в точности равна w₀, амплитуда колебания становится бесконечной. Этого, конечно, не может быть, потому что многие вещи, например трение, ограничивают амплитуду, а мы их не учитывали. Изменим теперь (23.2) так, чтобы учесть трение.

Сделать это обычно довольно трудно, потому что силы трения очень сложны. Однако во многих случаях можно считать, что сила трения пропорциональна скорости движения объекта. Именно такое трение препятствует медленному движению тела в масле или другой вязкой жидкости. Когда предмет стоит на месте, на него не действуют никакие силы, но чем скорее он движется и чем быстрее масло должно обтекать этот предмет, тем больше сопротивление. Таким образом, мы предположим, что в (23.2), кроме уже написанных членов, существует еще один — сила сопротивления, пропорциональная скорости: F_f=-c(dx/dt). Удобно записать с как произведение m на другую постоянную g, это немного упростит уравнение.

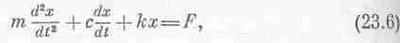
Мы уже проделывали такой фокус, когда заменяли k на mw²₀, чтобы упростить вычисления. Итак, наше уравнение имеет вид

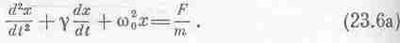
или, если положить с=mg и k=mw²₀ и поделить обе части на m,

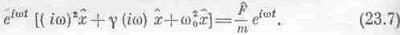
Это самая удобная форма уравнения. Если g очень мало, то мало и трение, и, наоборот, большие значения g соответствуют громадному трению. Как решать это новое линейное уравнение? Предположим, что внешняя сила равна F₀cos(wt+D); можно было бы подставить это выражение в (23.6а) и попытаться решить полученное уравнение, но мы применим наш новый метод. Представим F как действительную часть 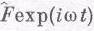, a x — как действительную часть 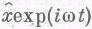и подставим эти комплексные числа в (23.6а). Собственно говоря, и подставлять-то нечего; внимательно посмотрев на (23.6а), вы тут же скажете, что оно превратится в

[Если бы мы попытались решить (23.6а) старым прямолинейным способом, то оценили бы по достоинству магический «комплексный» метод.] Поделив обе части уравнения на exp(iwt), найдем отклик осциллятора 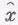на силу

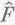
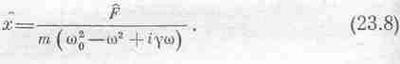
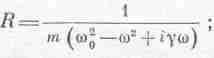
Итак, отклик x равен силе F, умноженной на некоторый множитель. Этот множитель не имеет ни названия, ни какой-то своей собственной буквы, и мы будем обозначать его буквой R:

тогда

Этот множитель можно записать либо как p+iq, либо как рехр(iq). Запишем его в виде рехр(iq) и посмотрим, к чему это приведет. Внешняя сила — это действительная часть числа F₀ехр(iD)ехр(iwt), она равна F₀cos(wt+D). Уравнение (23.9) говорит нам, что отклик 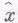равен 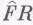; мы условились

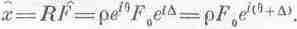
писать R в виде R=rехр(iq); следовательно,

Вспомним (об этом уже говорилось), что физическое значение х, равное действительной части комплексного числа х, равно действительной части rF₀exp[i(q+D)]exp(iwt). Но r и F₀ — действительны, а действительная часть ехр[i(q+D+wt)] — это просто cos(wt+D+q). Таким образом,

x=rF₀cos(wt+D+q). (23.10)

Это значит, что амплитуда отклика равна амплитуде силы F, умноженной на коэффициент усиления r; мы нашли «размах» колебаний. Но это еще не все: видно, что х колеблется не в такт с силой; фаза силы равна D, а у x; она сдвинута на дополнительную величину q. Следовательно, r и q — это величина и фазовый сдвиг отклика.

Найдем теперь значение r. Квадрат модуля любого комплексного числа равен произведению этого числа на комплексно сопряженное, т. е.

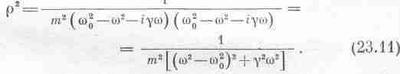
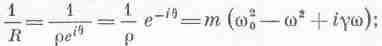
Можно найти и фазовый угол q

значит,

Знак минус возник оттого, что tg(-q) =-tgq. Угол q отрицателен при всех значениях w, т. е. смещение х отстает по фазе от силы F.

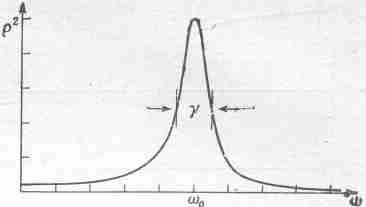
На фиг. 23.2 показано, как изменяется r² при изменении частоты (r² для физика интереснее, чем r, потому что r² пропорционально квадрату амплитуды, а значит, и той энергии, которую передает осциллятору внешняя сила).

Фиг.23.2. График зависимости r² от w.

Очевидно, что если gмало, то основной член в (23.11) — это 1/(w²₀-w²)², и отклик стремится к бесконечности, если w приближается к w₀. Но эта «бесконечность» — не настоящая бесконечность, потому что даже если w=w₀, то все еще остается слагаемое 1/g²w². Зависимость сдвига фазы от частоты изображена на фиг. 23.3.

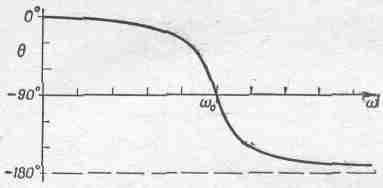
Фиг. 23.3. График зависимости q от w.

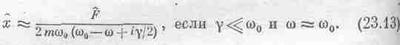
Иногда приходится иметь дело с формулой, немного отличающейся от (23.8); она тоже называется «резонансной» и, несмотря на некоторое отличие от (23.8), описывает те же самые явления. Дело в том, что если значение g очень мало, то наиболее интересная область резонансной кривой лежит около частоты w=w₀, а здесь при малых g формулу (23.8) с большой степенью точности можно заменить приближенной формулой. Поскольку w²₀-w²=(w₀-w)(w₀+w), то для w, очень близких к w₀, разность квадратов почти равна 2w₀(w₀-w), a gw можно заменить на gw₀. Значит, w²₀-w²+gw»2w₀(w₀-w+ig/2) и

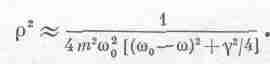
Легко найти и r²:

А теперь решите сами такую задачу: с увеличением частоты значение r² сначала растет, достигает при w₀ максимума, а потом снова убывает. На каком расстоянии от w₀ расположены частоты, которым соответствуют значения r², вдвое меньшие максимального? Покажите, что при очень малом g эти точки отстоят друг от друга на расстояние Dw=g. Это значит, что резонанс делается более острым по мере того, как влияние трения становится все слабее и слабее.

Другой мерой ширины резонанса может служить «добротность» q=w_o/g (чем уже резонанс, тем больше Q); если Q=1000, то по шкале частот ширина резонансной кривой равна всего 0,001. Резонансной кривой на фиг. 23.2 соответствует Q=5.

Явление резонанса важно потому, что оно проявляется довольно часто; описанию некоторых видов этих проявлений мы посвятим остаток главы.

§ 3. Электрический резонанс

Простейшие и самые широкие технические применения резонанс нашел в электричестве. Имеется довольно много устройств, из которых собираются электрические цепи. Их часто называют пассивными элементами цепи, и бывают они трех типов, хотя в каждый элемент одного типа всегда примешано чуточку элементов других типов. Прежде чем подробно описать эти элементы, заметим, что наше представление о механическом осцилляторе как о массе, подвешенной к концу пружины, всего лишь приближение. В «массе» сосредоточена вовсе не вся масса системы: пружина тоже обладает какой-то массой, пружина тоже инерционна. Точно так же «пружина» не состоит из одной пружины, масса тоже немного упруга, а не абсолютно тверда, как это может показаться. Подпрыгивая вверх и вниз, она слегка изгибается под толчками пружины. Так же обстоит дело и в электричестве. Расположить все предметы по «элементам цепи» с чистыми, идеальными характеристиками можно только приближенно. Так как у нас нет времени обсуждать пределы таких приближений, мы просто предположим, что они допустимы.

Итак, о трех элементах цепи. Первый называется емкостью (фиг. 23.4); в качестве примера емкости могут служить две металлические пластинки, разделенные тонким слоем диэлектрика.

Фиг. 23.4. Три пассивных элемента цепи.

Если пластинки зарядить, то между ними возникает разность потенциалов. Та же самая разность потенциалов будет между точками А и В, потому что при любой дополнительной разности потенциалов вдоль соединительных проводов заряды стекут по проводам. Таким образом, заданной разности потенциалов V между пластинками соответствуют определенные заряды +q и -q на каждой пластинке. Между пластинками существует некое электрическое поле; мы даже вывели соответствующую формулу для него (см. гл. 13 и 14)

V=sd/e₀=qd/e₀A , (23.14)
где d — расстояние между пластинками, А — площадь пластинок. Заметим, что разность потенциалов линейно зависит от заряда. Если построить емкость не из параллельных пластин, а придать отдельным электродам какую-нибудь другую форму, разность потенциалов будет по-прежнему пропорциональна заряду, но постоянную пропорциональности не так-то легко будет рассчитать. Однако надо знать только одно: разность потенциалов между концами емкости пропорциональна заряду V=q/C; множитель пропорциональности равен 1/С (С и есть емкость объекта).
Второй элемент цепи называется сопротивлением; этот элемент оказывает сопротивление текущему через него электрическому току. Оказывается, что все металлические провода, а также многие другие материалы сопротивляются току одинаково; если к концам куска такого материала приложить разность потенциалов, то электрический ток в куске I=dq/dt будет пропорционален приложенной разности потенциалов
V=RI=R(dq/dt). (23.15)
Коэффициент пропорциональности называют сопротивлением R. Соотношение между током и разностью потенциалов вам, наверное, уже известно. Это закон Ома.
Если представлять себе заряд, сосредоточенный в емкости, как нечто аналогичное смещению механической системы х, то электрический ток dq/dt аналогичен скорости, сопротивление R аналогично коэффициенту сопротивления g, а 1/С аналогично постоянной упругости пружины k. Самое интересное во всем этом, что существует элемент цепи, аналогичный массе! Это спираль, порождающая внутри себя магнитное поле, когда через нее проходит ток. Изменение магнитного поля порождает на концах спирали разность потенциалов, пропорциональную dI/dt. (Это свойство спирали используется в трансформаторах.) Магнитное поле пропорционально току, а наведенная разность потенциалов (так ее называют) пропорциональна скорости изменения тока
V=L(dI/dt)=L(d²q/dt²). (23.16)
Коэффициент L — это коэффициент самоиндукции; он является электрическим аналогом массы.
Предположим, мы собираем цепь из трех последовательно соединенных элементов (фиг. 23.5); приложенная между точками 1 и 2 разность потенциалов заставит заряды двигаться по цепи, тогда на концах каждого элемента цепи тоже возникает

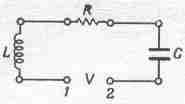
разность потенциалов: на концах индуктивности V_L=L(d²q/dt²), на сопротивлении V_R=R(dq/dt), а на емкости V_c=q/C.
Фиг. 23.5. Электрический колебательный контур, состоящий из сопротивления, индуктивности и емкости.

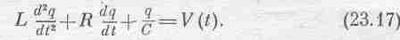
Сумма этих напряжений дает нам полное напряжение

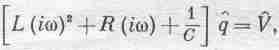
Мы видим, что это уравнение в точности совпадает с механическим уравнением (23.6); будем решать его точно таким же способом. Предположим, что V(t) осциллирует; для этого надо соединить цепь с генератором синусоидальных колебаний. Тогда можно представить V(t) как комплексное число V, помня, что для определения настоящего напряжения V(t) это число надо еще умножить на exp(iwt) и взять действительную часть. Аналогично можно подойти и к заряду q, а поэтому напишем уравнение, в точности повторяющее (23.8): вторая производная q— это (iw)²q, а первая — это (iw)q. Уравнение (23.17) перейдет в

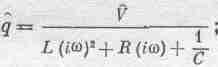
или
последнее равенство запишем в виде

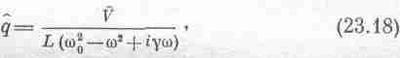
где w²₀=1/LC, a g=R/L. Мы получили тот же знаменатель, что и в механической задаче, со всеми его резонансными свойствами! В табл. 23.1 приведен перечень аналогий между электрическими и механическими величинами.
Таблица 23.1 · МЕХАНИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ВЕЛИЧИНЫ

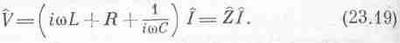
Еще одно чисто техническое замечание. В книгах по электричеству используют другие обозначения. (Очень часто в книгах на одну и ту же тему, написанных людьми разных специальностей, используются различные обозначения.) Во-первых, для обозначения Ц-1 используют букву j, а не i (через i должен обозначаться ток!). Во-вторых, инженеры предпочитают соотношение между V и I, а не между V и q. Они так больше привыкли. Поскольку I=dq/dt=iwq, то вместо q можно подставить I/iw, и тогда
Можно слегка изменить исходное дифференциальное уравнение (23.17), чтобы оно выглядело более привычно. В книгах часто попадается такое соотношение:

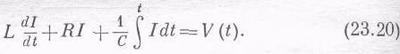
Во всяком случае, мы находим, что соотношение (23.19) между напряжением V и током I то же самое, что и (23.18), и отличается только тем, что последнее делится на iw. Комплексное число R +iwL+1/iwC инженеры-электрики часто называют особым именем: комплексный импеданс Z. Введение новой буквы позволяет просто записать соотношение между током и сопротивлением в виде V=ZI. Объясняется это пристрастие инженеров тем, что в юности они изучали только цепи постоянного тока и знали только сопротивления и закон Ома: V=RI. Теперь они более образованы и имеют уже цепи переменного тока, но хотят, чтобы уравнения были те же самые. Вот они и пишут V=ZI, и единственная разница в том, что теперь сопротивление заменено более сложной вещью: комплексным числом. Они настаивают на том, что они не могут использовать принятого во всем мире обозначения для мнимой единицы и пишут j; поистине удивительно, что они не требуют, чтобы вместо буквы Z писали букву R! (Много волнений доставляют им разговоры о плотности тока; ее они тоже обозначают буквой j. Сложности науки во многом связаны с трудностями в обозначениях, единицах и прочих выдумках человека, о чем сама природа и не подозревает.)
§ 4. Резонанс в природе
Хотя мы детально разобрали вопрос о резонансе в электрических цепях, можно приводить пример за примером из любых наук и отыскивать в них резонансные кривые. В природе очень часто что-нибудь «колеблется» и так же часто наступает резонанс. Об этом уже говорилось в одной из предыдущих глав; приведем теперь некоторые примеры. Зайдите в библиотеку, возьмите с полки несколько книг, полистайте их; вы обнаружите кривые, похожие на кривые фиг. 23.2, и уравнения, похожие на уравнения, приведенные в этой главе. Много ли найдется таких книг? Для убедительности возьмем всего пять-шесть книг, и они обеспечат вас полным набором примеров резонансов.
Первые два относятся к механике. Самый первый грандиозен — речь идет о колебаниях атмосферы. Если бы атмосфера, которая, по нашим представлениям, шарообразна и обволакивает нашу Землю равномерно со всех сторон, под влиянием Луны вытянулась бы в одну сторону, то атмосфера приняла бы форму вытянутой дыни. Если предоставить атмосферу, имеющую форму дыни, самой себе, то возникнут колебания. Так получается осциллятор. Этими колебаниями управляет Луна, которая вращается вокруг Земли. Чтобы понять, как это происходит, представим себе, что Луна стоит неподвижно на каком-то расстоянии от Земли, а Земля вращается вокруг своей оси. Поэтому проекция силы, скажем, на ось х имеет периодическую составляющую. Отклик атмосферы на приливно-отливные толчки Луны будет обычным откликом осциллятора на периодическую силу. Кривая bна фиг. 23.6 изображает ожидаемый отклик атмосферы (кривая а приведена на заимствованном нами рисунке из книги Мунка и Мак-Дональда по другому поводу и нас не касается). Может показаться странным, что удалось начертить эту кривую: ведь Земля вращается с постоянной скоростью, и поэтому можно получить только одну точку на кривой — точку, приблизительно соответствующую периоду 12 — 12,7 час (приливы бывают дважды в сутки) плюс еще немного, потому что надо учесть движение Луны. Но, измеряя величину атмосферных приливов и время их задержки — фазу, можно найти обе характеристики отклика r и q. По ним можно вычислить w₀и g а затем начертить уже всю кривую! Вот пример чистой науки. Из двух чисел получают два числа, по этим двум числам чертят очень красивую кривую, которая, конечно, проходит через ту же точку, по которой построена кривая! Кривая эта, конечно, бесполезна, пока нельзя измерить еще чего-нибудь, а в геофизике сделать это зачастую очень трудно. В нашем случае тем, что нужно было бы еще измерить, могут служить колебания атмосферы с собственной частотой w₀; необходимо какое-то возмущение, которое бы заставило атмосферу колебаться с частотой w₀. Такой случай однажды представился. В 1883 г. произошло извержение вулкана Кракатау, в результате которого в атмосферу взлетело пол-острова. Взрыв был такой, что удалось измерить период колебаний атмосферы. Он оказался равным 10¹/₂ час. Собственная частота w₀, полученная из кривой фиг. 23.6, была равна 10 час 20 мин; таким образом было получено по крайней мере хоть одно подтверждение правильности наших представлений об атмосферных приливах.

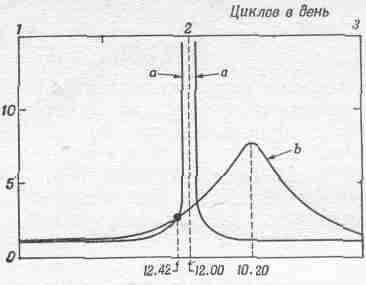
Фиг. 23.6. Влияние внешнего возбуждения на атмосферу.
Во втором примере речь пойдет о совсем малых колебаниях. Мы рассмотрим кристалл хлористого натрия, который состоит из расположенных друг возле друга ионов натрия и хлора (мы об этом говорили ранее). Ионы эти несут электрический заряд: первый — положительный, второй — отрицательный. Посмотрим, какие интересные колебания могут возникнуть в кристалле. Если отодвинуть все положительные заряды вправо, а отрицательные — влево и предоставить их самим себе, то они начнут колебаться взад и вперед: решетка ионов натрия против решетки ионов хлора. Но как растащить эти заряды? Очень просто: если внести кристалл в электрическое поле, оно отодвинет положительные заряды в одну сторону, а отрицательные — в другую! Значит, имея внешнее электрическое поле, можно, пожалуй, вызвать колебания кристалла. Но для этого частота электрического поля должна быть столь большой, что она соответствует инфракрасному излучению! Таким образом попытаемся построить резонансную кривую, измеряя поглощение инфракрасного света хлористым натрием. Такая кривая изображена на фиг. 23.7.

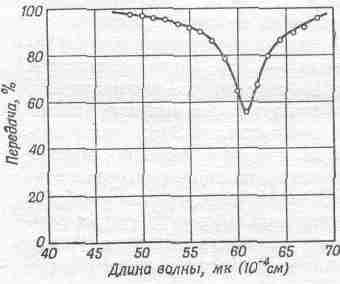
Фиг. 23.7. Прохождение инфракрасного излучения через тонкую (0,17 мк) пленку поваренной соли.
По абсциссе отложена не частота, а длина волны, но это техническая деталь; между частотой и длиной волны существует строго определенное соотношение, так что мы все-таки имеем дело со шкалой частот, и одна из этих частот— резонансная частота.
Ну, а что можно сказать о ширине резонансной кривой? Чем эта ширина определяется? Очень часто кривая выглядит гораздо шире, чем ей предписывается теоретическим значением g (эта ширина называется естественной шириной). Есть две причины уширения резонансной кривой. Мы наблюдаем колебания многих осцилляторов сразу, а их частоты могут немного отличаться. К этому приводят, например, натяжения в отдельных частях кристалла. Поэтому мы видим сразу много резонансных кривых, проходящих рядом. Они сливаются в одну кривую с большей шириной. Вторая причина очень проста — не всегда можно точно измерить частоту. Сколько со спектрометром ни возись, он всегда зарегистрирует не одну частоту, а целый спектр частот Dw. Поэтому может оказаться, что разрешающая сила спектрометра недостаточна для определения точной формы кривой. Так или иначе, но, глядя на фиг. 23.7, трудно сказать, что там за ширина — естественная или та, что соответствует неоднородностям кристалла или разрешающей силе спектрометра.
Еще один пример —более хитрый. Посмотрим, как качается магнит. Если поместить магнит в постоянное магнитное поле, то северный полюс захочет повернуться в одну сторону, а южный — в другую, и если магнит может поворачиваться вокруг оси, он будет колебаться около положения равновесия, как это делает стрелка компаса. Однако магниты, о которых пойдет речь,— это атомы. Они обладают моментом количества движения, и вращение порождает не простое движение в направлении поля, а прецессию. Посмотрим со стороны на какую-нибудь составляющую «шатаний», а потом возмутим колебания или попробуем управлять ими, чтобы затем измерить поглощение.
На фиг. 23.8 изображена кривая поглощения — типично резонансная кривая.

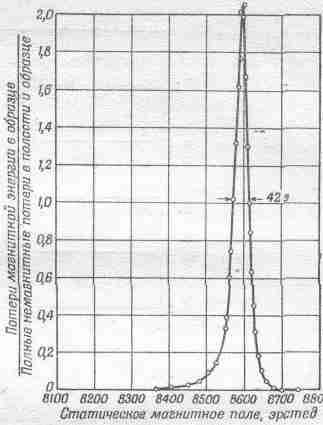
Фиг. 23.8. Зависимость потери, магнитной энергии в парамагнитном органическом соединении от напряженности приложенного поля.
Только получена она немного не так, как предыдущая. Частота горизонтального поля, управляющего колебаниями, все время остается постоянной, хотя, казалось бы, экспериментатор, чтобы получить кривую, должен менять частоту. Можно поступить и так, но технически легче оставить и неизменной, а менять напряженность постоянного поля, что соответствует изменению w₀ в нашей формуле. Таким образом мы имеем дело с резонансной кривой для w₀. Тем не менее мы получаем резонанс с определенными w₀ и g.
Пойдем дальше. Следующий наш пример связан с атомным ядром. Движение протонов и нейтронов в ядре — в некотором смысле колебательное движение. Убедиться в этом можно при помощи такого эксперимента: давайте обстреливать ядра лития протонами. Мы обнаружим, что в ядрах при этом будут происходить какие-то реакции, в результате которых возникает g-излучение. Кривая, изображающая количество испущенного излучения, имеет очень острый, типично резонансный максимум. Это изображено на фиг. 23.9. Однако приглядитесь к рисунку повнимательнее: на горизонтальной шкале отложена не частота, как обычно, а энергия! Дело в том, что та величина, которую в классической физике мы привыкли считать энергией, в квантовой механике оказывается определенным образом связанной с частотой некоторой волны. Если в привычной нам крупномасштабной физике при анализе какого-нибудь явления приходится иметь дело с частотой, то в квантовомеханических явлениях, связанных с атомным веществом, аналогичные кривые будут зависеть от энергии. Кривая на фиг. 23.9 иллюстрирует эту связь. Размышляя над этой кривой, можно прийти к мысли, что частота и энергия имеют глубокую взаимосвязь; так оно и есть на самом деле.
Вот еще одна резонансная кривая, полученная в результате опытов с атомными ядрами; она очень узкая, уже всех предыдущих. На фиг. 23.10 величина w₀ соответствует энергии 10 000 эв, а ширина g равна приблизительно 10^-5эв; иначе говоря, Q=10¹⁰!

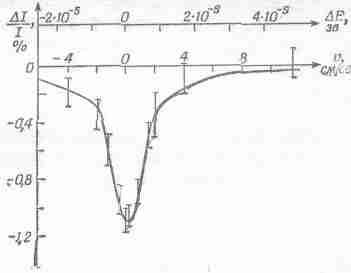
Фиг. 23.10. Кривая поглощения g-излучения, полученная Р. Мёссбауэром.
Построив такую кривую, экспериментатор измерил Q самого добротного из ныне известных осцилляторов. Это проделал Р. Мёссбауэр, получивший за свои работы Нобелевскую премию. На горизонтальной шкале отложена скорость, потому что для сдвига частоты использовался эффект Допплера, получающийся в результате относительного движения источника и поглотителя. Цифры дают некоторое представление о тонкости эксперимента — пришлось измерять скорости в несколько сантиметров в секунду! Если продолжить горизонтальную шкалу влево, то нулевую частоту мы найдем на расстоянии 10¹⁰ см! Страницы для этого, пожалуй, не хватит!
Наконец, возьмем какой-нибудь выпуск журнала Physical Review, скажем, за 1 января 1962 г. Найдется ли в нем резонансная кривая? Резонансные кривые имеются непременно в каждом выпуске этого журнала, и на фиг. 23.11 изображена одна из таких кривых.

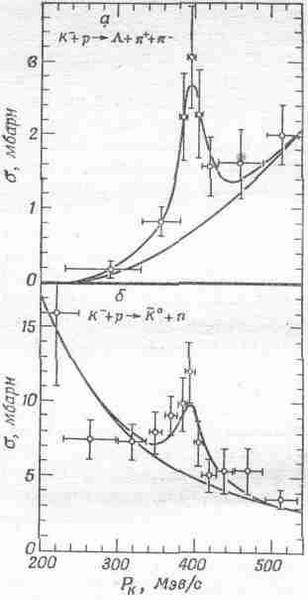
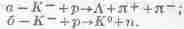
Фиг. 23.11. Зависимость эффективных сечений реакций от величины момента количества движения.
Нижняя кривая описывает нерезонансный фон; верхняя кривая показывает, что на зтот фон наложено резонансное сечение.
Это очень интересная кривая. Она соответствует резонансу в реакциях со странными частицами (K^--мезоны и протоны). Резонанс был обнаружен при измерении количества частиц разных сортов, получающихся в результате реакции. Разным продуктам реакции соответствуют разные кривые, но в каждой из них при одной и той же энергии есть пики примерно одинаковых очертаний. Значит, при определенной энергии K^--мезона существует резонанс. При столкновении К^--мезонов и протонов, наверное, создаются благоприятные для резонанса условия, а может быть, даже новая частица. Сегодня мы еще не можем сказать, что такое эти выбросы в кривых — «частица» или просто резонанс. Очень узкий резонанс соответствует очень точно отмеренному количеству энергии; это бывает тогда, когда мы имеем дело с частицей. Когда резонансная кривая уширяется, то становится трудно сказать, с чем мы имеем дело — с частицей, которая живет очень мало, или просто с резонансом в реакции. В гл. 2 мы отнесли эти резонансы к частицам, но когда писалась та глава, об этом резонансе еще не было известно, поэтому нашу таблицу элементарных частиц можно дополнить!