Глава 33. Электрические заряды и поля: электростатика

…Закон Кулона. Одноименные заряды отталкиваются, а разноименные притягивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними… во всех явлениях атомной и молекулярной физики, во всех твердых телах, жидкостях и газах и во всех явлениях, затрагивающих наши взаимоотношения с окружающим нас миром; единственная действующая сила, кроме тяготения, — это какое-либо проявление силы, описываемой этим простым законом. Силы трения, сила ветра, химические связи, вязкость, магнетизм, силы, заставляющие вертеться колеса фабрик и заводов, — все эти явления — не что иное, как закон Кулона…

Дж. Р. Захариас В журнале «Science», 8 марта 1957 г.

Изучению покоящегося электричества — «электростатике» — обычно отводится значительное место в курсе элементарной физики. Это дань застывшей традиции: ведь два столетия назад сведениями о покоящихся зарядах исчерпывались все знания об электричестве. Начинать изучение современных электрических цепей с электростатики — неправильный подход, и мы отказались от него. Кое-какие познания в электростатике вам, правда, понадобятся для изучения атомной физики. Насколько много вы увидите и узнаете из этой области физики, будет зависеть от аппаратуры, от погоды и от преподавателя. В общем, чем меньше, тем лучше.

Покоящиеся электрические заряды

Если электрическая цепь не замкнута, то ток по ней не течет. Но когда к незамкнутой цепи подключают батарею, по цепи протекают кратковременные токи, как показано на фиг. 51.

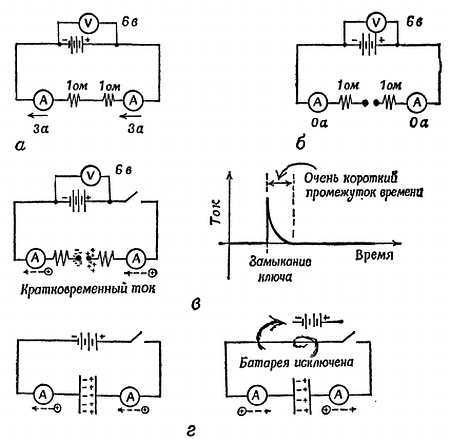
Фиг. 51. Кратковременные токи.

_{а — цепь замкнута, установившийся ток; б — цепь с разрывом, установившегося тока нет; в — цепь с разрывом; кратковременный «зарядный ток» при замыкании ключа, для обнаружения которого требуется весьма чувствительный прибор; г — цепь, в разрыв которой введены пластины; кратковременные «зарядный» и «разрядный» токи большей величины.}

Если оба провода в месте разрыва цепи заканчиваются большими пластинами из листового металла (образующими «конденсатор»), то кратковременные «зарядные токи» больше по величине, или протекают более продолжительное время. В течение доли секунды протекает несколько «кулон/сек». Следовательно, сколько-то «кулонов» должно пройти от батареи к пластинам и остаться там, прежде чем поток зарядов прекращается. Измерительные приборы показывают, что положительный ток течет к одной пластине и от другой пластины (или что к другой пластине течет отрицательный ток). Поэтому мы считаем, что, следовательно, на пластинах имеются заряды «+» на одной и «—» на другой, и говорим, что пластины «заряжены».

Если отсоединить батарею и включить вместо нее в цепь кусок проволоки, то потечет кратковременный ток в обратном направлении, пластины будут «разряжаться» через проволоку. Но пока это не сделано, заряды остаются на пластинах, отталкиваются батареей или удерживаются каким-то притяжением, действующим в промежутке между пластинами[39].

Можно показать, что пластины, будучи заряженными, действительно, притягивают друг друга. Сделайте пластины легкими и гибкими, например возьмите полоски тонкого листового металла и подведите к ним заряды от батареи. После того как пластины зарядятся, они притянутся друг к другу. Чем больше напряжение батареи (э.д.с.), тем больше притяжение. Это можно использовать для построения простейшего вольтметра. Для этого следует взять одну пластину в виде тонкого листочка металла и подвесить ее внутри металлической коробки, играющей роль второй пластины.

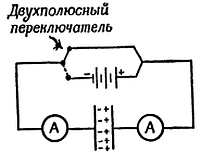
Фиг. 52. Двухполюсным переключателем батарею включают в цепь или отключают батарею и замыкают цепь без нее. Амперметры А и А показывают одинаковые кратковременные токи, текущие в одну пластину из другой. (Опыт 7 гл. 41.)

Когда между подвешенным листком и коробкой прикладывают напряжение, листочек отклоняется в направлении ближайшей стороны коробки. Угол отклонения указывает напряжение (в неравномерной шкале). Этот старинный прибор, которым пользуются еще и сейчас, носит название «электроскопа с золотыми листочками». Это идеальный вольтметр: он не потребляет тока (если не считать тока в момент подключения), но он очень слабо реагирует на разность потенциалов, меньшую примерно 300 в. Будучи однажды заряжены, металлические предметы остаются заряженными после отсоединения батареи, если они укреплены на изолирующих опорах, и к ним не прикасаются, скажем, металлической проволокой или влажными пальцами. Подсоедините две гибкие пластины А и В (или два воздушных шарика с металлическим покрытием на проводящих нитях) к зажимам «+» и «—» батареи: они притягиваются друг к другу. Укрепите теперь пластины А и В, заряженные «+» и «—», на изоляторах и зарядите еще одну пару пластин, А' и В', тоже соответственно «+» и «—». Поднесите А' к А: они отталкиваются (см. фиг. 54, г); В и В' тоже отталкиваются, тогда как А и В притягиваются. Вот почему нам нужны обозначения «+» и «—».

Фиг. 54. Электроскоп.

Две пластины, присоединенные к батарее, обладают противоположными зарядами и притягиваются; эти заряды исчезают («нейтрализуются»), если убрать батарею и соединить пластины куском проволоки.

Гибкие пластины или воздушные шарики не обладают никакими особыми электрическими свойствами — они были выбраны затем, чтобы малые электрические силы уравновешивались малыми силами тяжести. Так ведут себя любые металлические предметы (если только они укреплены на изоляторах, чтобы предотвратить появление токов, уносящих заряды). По проводникам (металл, графит и т. д.) заряды легко перемещаются. Вот почему можно до предела зарядить металлический предмет одним касанием провода от батареи. На изоляторах тоже могут собираться заряды, но лишь в том месте, где провод касается изолятора.

Батарея, присоединенная к двум изолированным металлическим предметам, быстро отталкивает к ним заряды до тех пор, пока разность потенциалов между предметами не станет равной э.д.с. батареи.

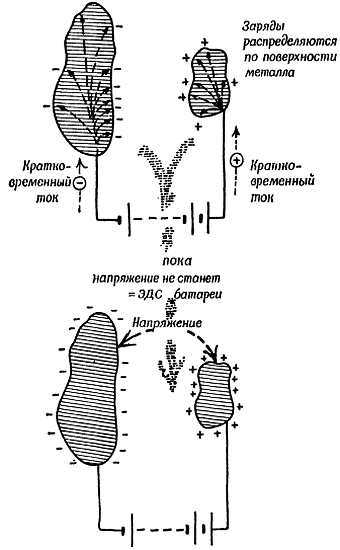
Фиг. 55. Движение зарядов.

Иногда нам кажется, что мы сообщаем заряд одному отдельно взятому предмету, и у нас возникает недоумение, куда девался заряд противоположного знака. Обычно можно убедиться в том, что он находится на окружающих телах: на коробке электроскопа, на стенах комнаты, на самой земле. Мы можем по небрежности оставить другой провод от батареи на влажном столе или полу, и по нему заряд противоположного знака, отталкиваемый батареей, будет отводиться «на землю». Или, напротив, намеренно присоединяем другой провод к водопроводной трубе, которая имеет соединение с землей. Если один зажим батареи «заземлен», то можно незаземленным проводом заряжать предметы. В этом случае говорят о потенциале заряженного тела, подразумевая разность потенциалов между этим телом и землей[40].

Но есть еще один замечательный способ заряжать тела, который годится для всех материалов. Он известен в течение столетий как способ, неразрывно связанный с учением об электростатике, о покоящемся электричестве. Подойдем теперь к нашей теме по-новому и рассмотрим простые явления, относящиеся к этому способу. Забудьте на мгновение то, что вы знаете о токах и зарядах, и проследите, как накапливались знания в далеком прошлом.

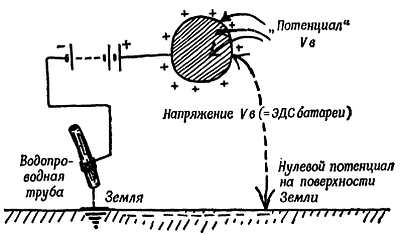
Фиг. 56.

Новый подход к изучению электростатики: заряжение тел «трением»

Потрите стержень из пластика, эбонита или сухого стекла куском ткани или меха: он будет притягивать пыль и маленькие кусочки бумаги. Два одинаковых натертых стержня отталкивают друг друга. Мы говорим, что они заряжены. На данном этапе «заряд» — это лишь наименование свойств «притягивать кусочки бумаги» и «отталкивать такие же тела»[41]. Мы представляем себе, что на поверхности стержней что-то скапливается, нечто такое, что мы называем электричеством, и это воображаемое скопление электричества именуется нами зарядом электричества, электрическим зарядом или просто зарядом. Можно показать, сняв поверхностный слой стержня, что заряд, который мы определяем таким образом, остается на поверхности стержня.

Проводники и изоляторы

Куском провода можно отвести заряды с поверхности заряженного тела, то же самое можно сделать, коснувшись поверхности пальцами или влажной нитью. Но с помощью изоляторов, например стекла или плексигласа, этого сделать нельзя. Возьмем образцы из различных материалов и прикрепим их к изолирующим ручкам так, чтобы любые заряды, приобретаемые образцами, не могли с них уходить. Мы обнаруживаем, что любые два разнородных материала, касаясь друг друга, становятся заряженными — металлы, неметаллы, элементы, соединения.

Силы взаимодействия между зарядами

Вскоре мы убеждаемся в том, что есть два рода зарядов; мы будем обозначать их через «+» и «—». Заряженные стержни из плексигласа или эбонита отталкивают друг друга, заряженные стержни из стекла (потертые о шелк) также отталкивают друг друга. Но заряженный плексиглас притягивает заряженное стекло. Если потереть стержень из плексигласа о мех, то оба тела — стержень и мех — становятся заряженными и притягивают друг друга. Мы называем отрицательными заряды, появляющиеся на эбоните, плексигласе, сере, и положительными — заряды на стекле и мехе, которым потерли плексиглас[42]. Силы взаимодействия между заряженными телами таковы: «+» и «+» отталкиваются, «—» и «—» отталкиваются, «+» притягивает «—» и «—» притягивает «+». Это можно выразить старой формулой:

ОДНОИМЕННЫЕ ЗАРЯДЫ ОТТАЛКИВАЮТСЯ, РАЗНОИМЕННЫЕ ЗАРЯДЫ ПРИТЯГИВАЮТСЯ.

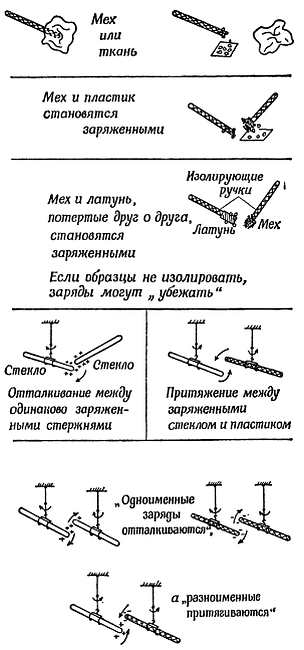
Фиг. 57. Электрические заряды.

Умножение зарядов: электрофор

Заряд большой величины легко получить с помощью электрофора — диска из плексигласа (или эбонита), заряжаемого трением о мех. Диск располагается на столе, заряжается его верхняя поверхность. Возьмите металлическую пластинку с изолирующей ручкой и зарядите ее следующим образом:

1) Поднесите металлическую пластинку на очень близкое расстояние к заряженному диску. (Не беда, если она коснется диска, поскольку диск — изолятор.)

2) Коснитесь одним пальцем металлической пластинки, присоединив ее (через руку, тело, подошвы обуви) на мгновение к земле. Затем уберите палец.

3) Снимите пластинку с диска. Пластинка теперь заряжена и легко может отдать часть заряда другим телам при соприкосновении с ними.

Сейчас нам кажется это бессмысленным занятием, чем-то вроде колдовского ритуала. Мы воспользуемся этим процессом для получения зарядов и объясним его позже, хотя вы могли бы отгадать объяснение, используя то, что уже знаете.

Заряд на диске остается неизменным, поэтому процесс можно повторить и получить бесконечный поток зарядов, поступающих на пластинку. Как вы думаете, откуда берется энергия?

Опыты с заряженной пластинкой, электроскопом и пробным шариком

Если заряженную пластинку электрофора поднести на близкое расстояние к чьему-нибудь вытянутому пальцу или к носу, то возникает искра, и пластинка теряет свой заряд. Человек, к которому поднесли пластинку, испытывает легкий электрический удар, но не остается заряженным, если он не стоит на изолирующей подставке.

Пластинку можно заряжать повторно и сообщать с помощью нее заряд какому-нибудь металлическому предмету, пока он почти не перестанет воспринимать заряд при дальнейших прикосновениях[43]. При прикосновении к такому заряженному предмету можно вызвать большую искру и ощутить электрический удар. Если к этому предмету прикоснуться другим изолированным металлическим предметом или соединить оба тела влажной нитью, или металлической проволокой, то часть заряда первого тела перейдет ко второму. При распределении заряда между нашим металлическим предметом и землей предмет, по-видимому, теряет весь заряд: если распределение происходит в пропорции к размерам, то на нем, действительно, останется немного.

Воздушным шарикам с металлическим покрытием, подвешенным на шелковых нитях, можно сообщить большие заряды и наблюдать отталкивание между ними. Можно изготовить электроскоп[44] «с золотыми листочками», подвесив на изоляторе одну или две полоски из тонкого листового металла. Это чувствительный прибор, служащий для обнаружения электрических зарядов. Он измеряет силу, действующую на листочек из-за наличия на нем заряда, благодаря уравновешиванию этой силы определенной долей силы тяжести. Электроскоп обычной конструкции состоит из металлического стержня, к которому привешен тонкий листочек. Стержень укреплен при помощи изолирующей пробки в верхней части металлического корпуса. Стержень заканчивается вверху за пределами корпуса шаром или пластинкой, через которые легко сообщить заряд листочку. Даже если просто поднести заряд на близкое расстояние, листочек отклоняется и остается в таком положении, пока заряд остается поблизости[45].

Чтобы перенести пробные заряды с какого-либо большого заряженного тела к листочку электроскопа, мы пользуемся маленьким пробным шариком. Каждая новая порция заряда увеличивает отклонение листочка. Если сообщить листочку некоторое количество положительного заряда, а потом подвести к нему небольшую порцию отрицательного заряда, то листочек слегка опустится. Это дает основание полагать, что новый заряд нейтрализовал какую-то долю прежнего. Таким образом, обозначения «+» и «—» оказываются вполне подходящими. Это дает в наше распоряжение простой способ обнаружения положительных и отрицательных зарядов.

С помощью пробного шарика и электроскопа можно исследовать распределение «плотности заряда», на поверхности какого-либо заряженного тела. Мы убеждаемся в том, что заряд распределяется неравномерно. Наибольшую величину поверхностная плотность заряда имеет на остриях, наименьшую — на вогнутостях. Продолжая эти наблюдения, зарядим полый металлический цилиндр и исследуем его. Оказывается, на внешней поверхности может быть распределено большое количество заряда, а на внутренней поверхности заряд отсутствует.

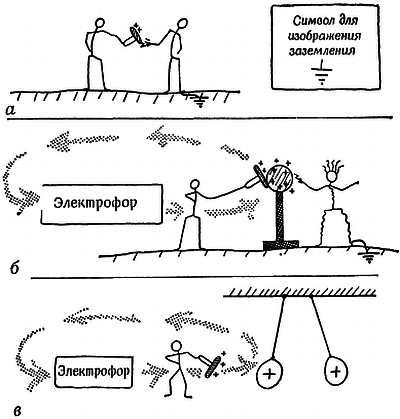
Фиг. 59. Электрические заряды.

_{а и б — удар током; в — между воздушными шариками, заряженными посредством многократного применения электрофора, наблюдается отталкивание. Воздушные шарики должны иметь проводящую поверхность, для этого их покрывают тонким слоем металла или графита.} 

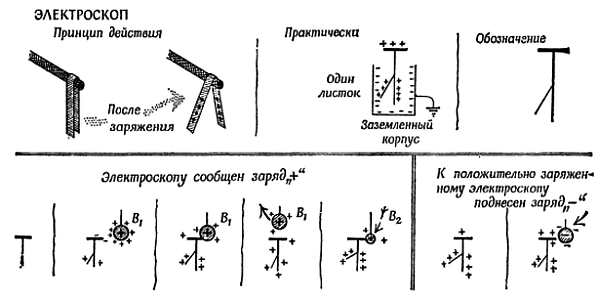
Фиг. 60. Электроскоп.

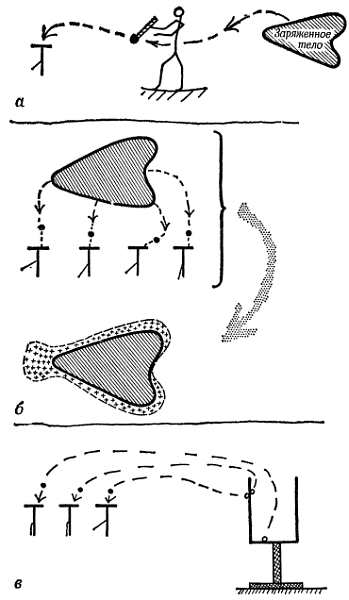
Фиг. 61. Распределение заряда.

_{а — исследование распределения заряда на проводнике; б — область со знаками «+» изображает поверхностную плотность заряда; в — распределение заряда на наружной и внутренней поверхностях заряженного полого металлического стакана.}

Задача 1

На изолирующую подставку помещен незаряженный металлический стакан. Внутрь стакана на шелковой нити опускают заряженный металлический шар, касаются шаром стакана изнутри и извлекают шар.

а) Какое количество заряда останется на шаре?

б) Какое количество заряда останется на шаре, если он касается стакана снаружи, а не изнутри?

Электростатическая индукция

Простое приближение заряда к электроскопу вызывает известный эффект. Исследуем этот эффект (его называют «наведением» или «индуцированием» зарядов, или «электростатической индукцией»). Зарядим большой металлический шар и поместим его вблизи от длинного металлического цилиндра с закругленными торцами. Возьмем маленький пробный шарик и электроскоп и посмотрим, какие заряды имеются на цилиндре. Предположим, что большой шар заряжен положительно. В этом случае мы обнаружим на ближнем конце цилиндра отрицательный заряд, у середины заряд отсутствует или его мало, а дальний конец цилиндра будет заряжен положительно. Мы считаем, что эти положительные и отрицательные заряды с самого начала имелись в незаряженном цилиндре и что произошло их разделение под влиянием заряда большого шара. Заряды свободно перемещаются по цилиндру, поэтому положительный заряд большого шара притягивает отрицательные заряды и отталкивает от себя положительные. Соедините теперь цилиндр с землей, коснувшись его пальцем. Уберите палец и снова посмотрите, как заряжен цилиндр. На цилиндре по-прежнему будет отрицательный заряд у конца, ближайшего к шару; положительных зарядов на удаленном конце цилиндра нет. Мы говорим, что они ушли через наш палец дальше, «на землю». (Путь зарядов: рука — тело — ноги — сырая обувь — сырой пол и т. д.). Как вы знаете, это движение зарядов можно продемонстрировать с помощью микроамперметра. Теперь уберите большой шар, на котором по-прежнему имеется положительный заряд. На цилиндре останется отрицательный заряд, плотность его на концах будет очень велика. Мы «создали» отрицательный заряд на цилиндре (без потери первоначального положительного заряда на большом шаре). Этот отрицательный заряд можно снять и как-то использовать. Описанный процесс можно повторить сколько угодно раз, получая порции отрицательных зарядов, которые могут быть посланы по проволоке в виде тока малой величины. Обратите внимание на последовательность наших действий после того, как мы зарядили большой шар: 1) приближаем к шару металлический цилиндр, 2) касаемся на мгновенье цилиндра пальцем, 3) убираем цилиндр и убеждаемся в наличии на нем заряда, который можно использовать. Этот процесс называют электризацией через влияние, а само явление — электростатической индукцией. Подумайте, где вы встречались с ним раньше? Откуда берется энергия, получаемая вместе с зарядом цилиндра?

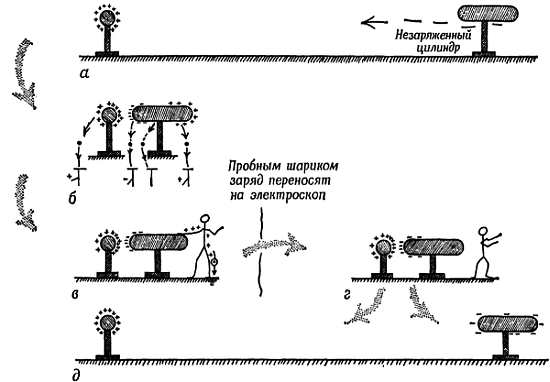
Фиг. 62. Стадии процесса электризации через влияние.

Задача 2

а) На стеклянном стержне имеется небольшой положительный заряд, полученный трением. Можно зарядить электроскоп, если «соскрести» некоторое количество заряда со стержня и перенести его на электроскоп. Как зарядится электроскоп: положительно или отрицательно?

б) Вы можете также создать заряд на электроскопе, поднеся к нему заряженный положительно стержень. Что вы должны будете затем сделать, чтобы часть заряда осталась постоянно на электроскопе, не приближая дальше стержень? Какой это будет заряд: «+» или «—»?

Теперь вы можете зарядить электроскоп положительно или отрицательно с помощью положительно заряженного стеклянного стержня. Попытайтесь сообщить дополнительный положительный и отрицательный заряд уже заряженному электроскопу.

Полые проводники (фиг. 63–65)

Поставьте небольшой металлический стакан сверху на электроскоп, так чтобы листочек мог воспринимать пробную порцию заряда стакана. Зарядите металлический шар В, держа его на изолирующей нити, и поднесите его на близкое расстояние к стакану снаружи. Чем ближе шар В поднесен к стакану, тем больше отклонение листочка — тем больше положительный заряд, отталкиваемый к электроскопу положительным зарядом шара В. Если вы коснетесь пальцем стакана или электроскопа, то листочек опускается до нуля. Но если вы после прикосновения уберете палец, а затем уберете шар, то на стакане и электроскопе останется отрицательный заряд — результат электризации через влияние. До этого, когда электроскоп показывал нуль, на стакане был отрицательный заряд, но он притягивался положительным зарядом шара, и к листочку никакого заряда не попадало. Такие заряды образно называют «связанными зарядами».

Начнем теперь опыт снова, когда стакан и электроскоп не заряжены, и опустим положительно заряженный шар внутрь стакана. Электроскоп показывает большой заряд, который остается неизменным, куда бы ни поместить шар В внутри стакана. Если В вынуть, то листочек опускается, если ввести снова, то восстанавливается прежнее отклонение листочка. Теперь коснитесь шаром В стакана: отклонение листочка остается тем же. Выньте шар В: сохраняется полное отклонение листочка. По-видимому, шар В отдал весь свой заряд. (Куда же мог уйти весь заряд шара В, приведенного в соприкосновение с внутренней поверхностью стакана?) Детально «объяснить» это можно так.

Мы говорим, что когда В находится внутри стакана, его положительный заряд удерживает равный по величине заряд противоположного знака на внутренней поверхности стакана (в виде «связанного заряда») и отталкивает такой же по величине положительный заряд к наружной поверхности первоначально нейтрального стакана и к электроскопу. Когда В касается внутренней поверхности стакана, оба заряда, находящиеся внутри стакана, получают возможность нейтрализовать друг друга. Шар В теряет весь свой заряд, но такой же заряд остается на внешней поверхности стакана. Это свойство полого цилиндра[46] находит различные применения. Два случая применения этого свойства рассмотрены в задачах 3 и 5.

Наблюдая электрические эффекты внутри заряженного металлического шара, мы можем даже проверить закон, который устанавливает характер силы взаимодействия между зарядами. Об этом говорится дальше.

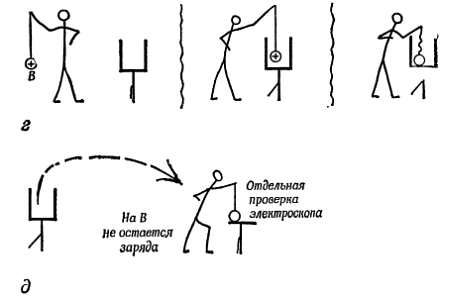
Фиг. 63, а — д.

Задача 3 (фиг. 64)

В генераторе Ван-де-Граафа на миллион вольт, который применяется в опытах по «расщеплению атомов», на огромном медном шаре накапливаются электрические заряды. Происходит это следующим образом. Внутрь медного шара одним своим концом заходит бесконечная шелковая лента, которая движется на двух роликах. Вне шара лента заряжается (например, с помощью простейшего устройства типа электрофора, описанного выше), а внутри шара лента касается проволоки-щетки. Почему заряды переходят с ленты на шар?

Фиг. 64. К задаче 3.

Генератор Ван-де-Граафа

Электрофор, наше простейшее устройство, рассмотренное выше, можно усовершенствовать и превратить в так называемую электрическую индукционную (или электростатическую) машину, приводимую в действие вращением. Электрической индукционной машиной широко пользовались в прошлом для исследовательских работ и в учебных целях. Теперь эта машина — анахронизм, но ею все еще пользуются для демонстрационных опытов.

Более современную машину представляет собой генератор Ван-де-Граафа, изготовленный впервые Робертом Ван-де-Граафом в Принстоне. Такими машинами пользуются теперь в атомных исследованиях для получения разности потенциалов в несколько миллионов вольт и ускорения заряженных частиц.

На фиг. 65 показана уменьшенная модель генератора Ван-де-Граафа.

Фиг. 65. Модель генератора Ван-де-Граафа.

Бесконечная шелковая лента, приводимая в движение от руки, переносит заряды в клетку. К ленте приклеены металлические пластинки. У нижнего конца ленты с помощью устройства, которое производит электризацию через влияние, каждой металлической пластинке сообщается небольшой положительный заряд. Поскольку шелк — хороший изолятор, заряды эти никуда не уходят, и лента переносит их в клетку. Внутри клетки упругая проволока, которая касается ленты, собирает имеющийся на пластинках заряд. Большой металлический листочек, привешенный снаружи клетки, показывает, как накапливается заряд.

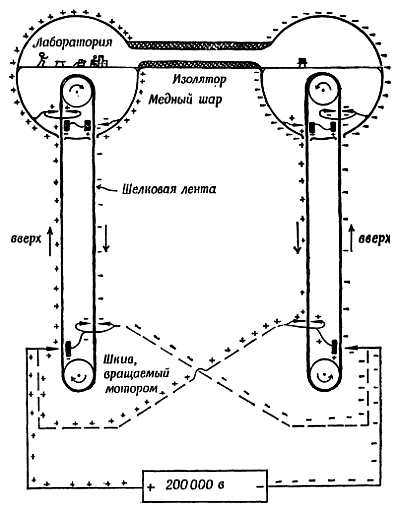
Фиг. 66. Сдвоенный генератор Ван-де-Граафа.

_{От источника с напряжением 200 000 в наносят положительные заряды на одну ленту, а отрицательные — на другую. Внутри огромной сферы с помощью остроумной схемы электризации через влияния (показана в упрощенной форме) заряды противоположного знака наносятся на нисходящую часть ленты, что облегчает работу источника. В очень крупных генераторах, дающих малый постоянный ток при разности потенциалов несколько миллионов вольт, важное значение имеют проблемы изоляции, и может лаже потребоваться поместить генератор в атмосферу сжатого газа.}

Задача 4

Объясните кратко, как положительные заряды переносятся на металлические пластинки на фиг. 65. Обратите внимание на то, что Р представляет собой металлическую пластинку, которая укреплена на изоляторе вблизи ленты, и несет отрицательный заряд; G — металлическая щетка, соединенная с землей, которая касается металлических пластинок вблизи Р.

В большой машине роль клетки играет огромный медный шар, иногда настолько больших размеров, что в нем могла бы разместиться настоящая лаборатория[47]. На шелковой ленте нет металлических пластинок, заряды остаются на самом шелке. Заряды наносятся на шелк внизу и снимаются вверху с помощью ряда острий, которые расположены на близком расстоянии от ленты, но не касаются ее[48].

Задача 5. Определение одинаковых и противоположных по знаку зарядов (фиг. 67)

К электроскопу прикреплен небольшой металлический стакан. В стакан вводят маленький кусочек плексигласа и маленький кусочек меха на изолирующих рукоятках. И плексиглас, и мех не заряжены. Если заряды, получаемые трением, равны и противоположны по знаку, то что, по вашему мнению, произойдет с электроскопом на каждой из следующих стадий опыта, если задано, что в стадии б) листочек отклоняется на 60°:

а) Мех и плексиглас потерты друг о друга внутри стакана (они не касаются стенок стакана).

б) Плексиглас извлекается из стакана (листочек отклоняется на 60°).

в) Мех также извлекается из стакана, не касаясь его.

г) Плексиглас снова вводится в стакан.

д) В стакан вводятся снова и плексиглас, и мех.

Фиг. 67. К задаче 5.

Сохранение заряда

Предметы, окружающие нас в повседневной жизни, кажутся незаряженными: между ними нельзя заметить притяжения или отталкивания; молекулы газа не обнаруживают тенденции перемещаться в каком-либо одном направлении в однородном электрическом поле. Если незаряженное вещество содержит положительные и отрицательные заряды, которые можно разделять или переносить, то они должны содержаться в равных количествах. Когда мы заряжаем предметы трением или с помощью батареи, то рассчитываем обнаружить равные количества противоположных по знаку зарядов.

Опыт, о котором идет речь в задаче 5, дает возможность произвести очень тонкую и вместе с тем важную проверку. Из этого опыта и опытов по наблюдению кулоновской силы взаимодействия зарядов можно заключить, что электрический заряд сохраняется: происходит обмен зарядами между телами без выигрыша или потери заряда, «создавать» можно только равные количества противоположных по знаку зарядов. Мы считаем, что этот фундаментальный принцип сохраняет силу и в атомной и ядерной физике.

Оказывается даже, что фотон излучения высокой энергии (который, конечно, не представляет собой ни вещества, ни электричества) превращается в пару электрон-позитрон с одинаковыми по величине и противоположными по знаку зарядами. Мы говорим о «зарядовом обмене» между некоторыми составными частями ядра — процесс этот происходит слишком быстро, чтобы его можно было описать языком механики, — и по-прежнему считаем закон сохранения заряда незыблемым.

Силы, с которыми заряды действуют друг на друга: закон Кулона

Электричество и заряды — это такие термины, которые употребляют в тех случаях, когда наблюдается отталкивание и притяжение. Силы отталкивания и притяжения словно исходят от заряженных тел в радиальных направлениях. Сила отталкивания или притяжения, с которой один заряд действует на другой, направлена вдоль прямой, соединяющей оба заряда, и уменьшается с увеличением расстояния между ними. Спустя столетие после того, как Ньютон открыл закон всемирного тяготения, французский физик Кулон исследовал экспериментальным путем силу взаимодействия между зарядами и показал, что она так же, как и сила тяготения, изменяется обратно пропорционально квадрату расстояния. Схема прибора Кулона показана на фиг. 68.

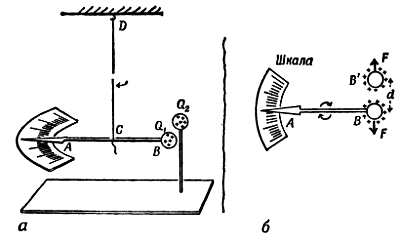
Фиг. 68. Крутильные весы Кулона.

_{а — вид сбоку; б — вид сверху.}

_{Сила оценивалась по углу закручивания нити. Заряженные шары тщательно изолировались. Весь прибор был закрыт, чтобы уменьшить влияние токов утечки через воздух.}

Он по существу не отличается от прибора, который Кавендиш примерно в это же время использовал для измерения гравитационной постоянной G. На изолирующем стержне АВ, подвешенном на тонкой нити CD, укреплен металлический шарик В, которому сообщен заряд. К шарику В приближают другой шарик В' и по мере приближения измеряют силу отталкивания по углу закручивания нити. Предполагая, что при закручивании нити справедлив закон Гука, Кулон сравнил силы взаимодействия при различных расстояниях d между В и В'. Он установил, что F изменяется пропорционально 1/d². Кулон изменял заряд Q одного шарика, а затем другого до ¹/₂ Q, ¹/₄ Q и т. д., измеряя в каждом случае силу взаимодействия, и установил (или, вернее, предположил и не обнаружил противоречий с этим предположением), что F изменяется пропорционально заряду шарика В(Q₁) и заряду шарика В'(Q₂).

Объединяя эти выводы, Кулон установил, что

F ~ Q₁∙Q₂/d², или F ~ ∙(Q₁∙Q₂/d²)

Это закон Кулона.  — универсальная постоянная, которая играет такую же роль, что и гравитационная постоянная G.

Задача 6

Кулон не располагал средствами для измерения зарядов Q₁ или Q₂. Тем не менее Кулон имел возможность при желании изменять заряд шарика Q до ¹/₂ Q и таким образом исследовать роль каждого из зарядов Q в выражении для силы взаимодействия*

а) Каким образом Кулону удавалось уменьшить заряд Q до ¹/₂ Q (Указание. Он располагал дополнительным металлическим шариком такого же размера.)

б) Какое предположение относительно природы заряда нужно сделать, прибегая к приему, используемому для решения задачи а)? (Фактически это предположение было сформулировано почти как аксиома при введении понятия электрического заряда. Сегодня мы можем в известной степени подтвердить его экспериментально путем счета электронов и наблюдая пары электрон-позитрон.)

Значение  зависит от выбора единиц измерения заряда точно так же, как значение постоянной G зависит от того, измеряем ли мы массу в килограммах или в фунтах. Мы будем пользоваться кулонами, с которыми вы уже встречались, когда шла речь о движении зарядов, а также метрами и ньютонами[49].

В этом случае значение  определяется экспериментально близким к 9 000 000 000, т. е. 9,0∙10⁹ ньютон∙м²/ кулон².

В нашем курсе не обязательно знать значение , однако, имея в виду проследить связь между законом Кулона и электрическими токами, интересно измерить это огромное число. Чтобы измерить B, нам понадобятся сведения об электрических полях. Мы еще вернемся к этому вопросу.

Проверка закона Кулона

ДЕМОНСТРАЦИОННЫЙ ОПЫТ

Можно приближенно произвести непосредственную проверку закона Кулона, измерив силу взаимодействия между двумя зарядами. Мы сообщаем большой заряд двум металлическим шарикам[50] и «взвешиваем» один шарик, когда второй удален от него на 0,1, 0,2, 0,3 м и т. д., считая расстояние между центрами.

Вам следовало бы посмотреть, как проделывается описываемый опыт, пусть это будут лишь грубые измерения, чтобы воочию убедиться в справедливости этого замечательного экспериментального закона. В задаче 7 приведен пример записи результатов измерений, позволяющий получить представление об этом опыте в том случае, если вам не удастся его посмотреть.

Задача 7. Проверка закона Кулона (фиг. 69)

Шарик А прикреплен к одному концу плексигласового коромысла. Слабая (но хорошая) стальная пружина уравновешивает вес шарика и позволяет измерить любую дополнительно действующую на шарик силу. У второго конца коромысла укреплена длинная стрелка, против которой расположена вертикальная шкала. Шарик В крепится отдельно на подвижном изолирующем стержне над шариком А. От стержня, на котором крепится шарик В, вниз отходит стержень из плексигласа с делениями, позволяющий измерить расстояние между шариками. Каждый шарик был заряжен с помощью электрофора. Шарик В относили на большое расстояние и устанавливали стрелку, связанную с шариком А, против нуля шкалы. Затем шарик В располагали над А на определенном расстоянии по вертикали и отсчитывали показание стрелки, по которому можно оценить силу отталкивания. (Шкала разбита на произвольные деления, каждое примерно по 1 см. Чтобы оценить жесткость пружины — нам она здесь не нужна, — на шарик А помещали груз 1 г; при этом отсчет по шкале равен 49.) Ниже в таблице приведена для примера запись результатов измерений («бесконечность» означает, что шарик В убран).

а) Перепишите таблицу, добавив столбец ДЛЯ ПРОВЕРКИ ЗАКОНА КУЛОНА. Проделайте вычисления с целью проверить обратную пропорциональность квадрату расстояния.

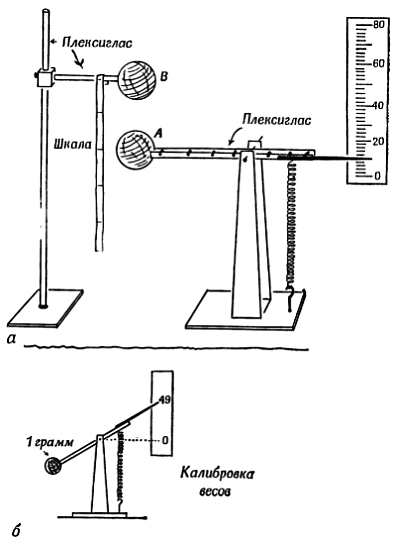
б) Предполагая, что значение 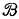 (которое мы измерим позже) равно 9,0∙10⁹, и считая оба заряда равными, оцените их величину в кулонах. (Обратите внимание на то, что сила должна быть выражена в ньютонах.)

Фиг. 69. Проверка закона обратной пропорциональности квадрату расстояния.

Электрические поля

Мы представляем себе, что с каждым зарядом связано электрическое поле, подобное в известном смысле полю тяготения. Напряженность электрического поля в любой точке определяют как силу, действующую на пробный кулон, помещенный в эту точку. Принимая во внимание, что 1 кулон — огромный заряд, сформулируем это определение более реалистически следующим образом:

НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ = СИЛА, ДЕЙСТВУЮЩАЯ НА МАЛЫЙ ПРОБНЫЙ ЗАРЯД / ВЕЛИЧИНА ПРОБНОГО ЗАРЯДА

Мы получаем силу, действующую на единичный заряд, в ньютон/кулон[51].

На фиг. 70 показаны «демоны», занятые экспериментальным исследованием напряженности поля тяготения и электрического поля.

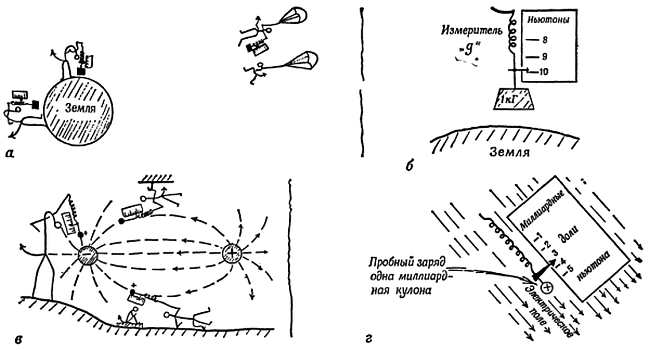
Фиг. 70. Измерение напряженности поля.

_{а и б — измерение напряженности гравитационного поля Земли; сила притяжения эталона килограмма измеряется в ньютонах; в — измерение напряженности электрического поля; г — «измеритель напряженности электрического поля».}

_{Чтобы избежать искажения измеряемого поля и не иметь дела при измерениях с огромными силами, пробный заряд должен быть значительно меньше, чем 1 кулон. Тогда мы должны будем измерять силу, действующую, скажем, на заряд в 1 миллиардную кулона, с помощью пружинных весов, проградуированных в миллиардных долях ньютона. При этом мы определим напряженность поля в ньютон/кулон.}

Напряженность поля вокруг малого изолированного заряда изменяется обратно пропорционально квадрату расстояния.

НАПРЯЖЕННОСТЬ ПОЛЯ = СИЛА, ДЕЙСТВУЮЩАЯ НА ПРОБНЫЙ ЗАРЯД / ПРОБНЫЙ ЗАРЯД =

То же самое справедливо для изолированного заряженного шара. Напряженность поля — вектор. Кроме величины, поле характеризуется направлением силы, действующей на положительный пробный заряд. Можно начертить карту направлений электрического поля с помощью воздушного шарика, реального или воображаемого, несущего малый пробный заряд. На фиг. 71 показаны два громадных металлических шара, заряженных положительно и отрицательно. Заряженный воздушный шарик будет перемещаться от одного шара к другому вдоль любой из траекторий, показанных пунктирными линиями. Они называются силовыми линиями. Эти линии указывают направление поля, т. е. направление результирующей силы, действующей на пробный заряд.

Фиг. 71. Определение конфигурации электрического поля.

_{Путем геометрического построения находят последовательно в разных точках направление результирующей силы, приложенной к пробному заряду.}

Силовые линии искривлены потому, что на пробный заряд действуют силы отталкивания со стороны одного заряда, +Q₁, и силы притяжения со стороны другого заряда, — Q₂, которые изменяются по направлению и по величине от точки к точке. Пользуясь правилом сложения векторов, можно найти конфигурацию силовых линий в подобных случаях, хотя это связано с утомительной процедурой. Предположим, два заряда, создающие поле, равны и противоположны по знаку. Пробный заряд q, помещенный в точку Р, испытывает силу отталкивания F₁ со стороны заряда Q₁ и меньшую силу притяжения F₂ со стороны заряда Q₂ (меньшую потому, что Q₂ дальше). Сложение этих сил дает результирующую силу R, действующую на q. В точке Р силовая линия поля направлена вдоль R. Повторим теперь это рассмотрение для другой, соседней точки Р' затем для точки Р" и т. д. Точка Р' выбрана на малом расстоянии от Р, отсчитанном практически вдоль силы R (которая указывает направление поля в Р), точка Р" взята на R'. Можно затем объединить эти построения и получить часть силовой линии. Существуют методы, приводящие к цели быстрее. В них используются более сложные геометрические представления, но в основе лежит тот же закон обратной пропорциональности квадрату расстояния. Эти методы дают целую сетку силовых линий и позволяют определить картину силовых линий других полей, например, показанных на фиг. 72.

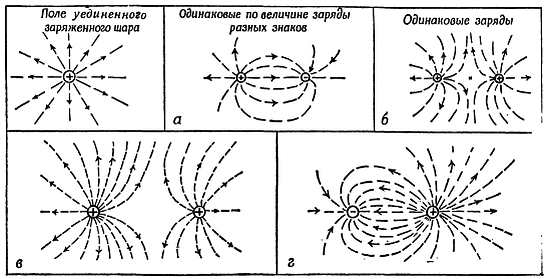
Фиг. 72. Картины электрических полей.

Задача 8

а) Заряды, поле которых показано на фиг. 72, в, не равны. Какой из них больше?

б) Дайте обоснование вашему ответу на вопрос а).

в) Дайте ответ на вопросы а) и б) для зарядов, поле которых показано на фиг. 72, г.

Картины электрического поля

Картину электрического поля можно получить, используя маленькие кусочки материала, которые способны выстраиваться вдоль силовых линий поля. Правда, эти демонстрационные опыты не позволяют «наблюдать» электрические поля столь же отчетливо, как магнитные поля с помощью железных опилок. Металлические предметы, имитирующие Q₁ и Q₂, заряжают какой-нибудь машиной, не останавливая ее, чтобы восполнять утечку заряда. Стеклянную ванну наполняют машинным маслом и в масло насыпают мелко настриженные волосы. Затем в ванну погружают металлические электроды. Волосы располагаются вдоль силовых линий поля. В кусочках волос создаются парные заряды, и они стремятся расположиться вдоль силовых линий. Вам следовало бы посмотреть эти картины электрических полей и сравнить их с аналогичными по конфигурации магнитными полями (см. гл. 34).

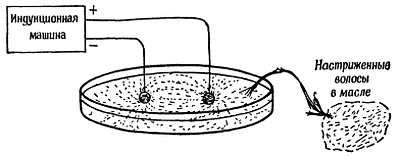
Фиг. 73. Определение конфигурации электрического поля опытным путем.

_{В чашу с густым маслом насыпают мелко настриженные волосы и создают сильное электрическое поле.}

На фиг. 74 показано электрическое поле, созданное равными и противоположными по знаку зарядами +Q и — Q, и магнитное поле вокруг стержневого магнита с «полюсами» +Р и — Р. Если на изображение электрического поля нанести контуры магнита, то обе картины будут в точности одинаковы. Обе построены, исходя из направления сил, обратно пропорциональных квадрату расстояния, которые действуют на воображаемое очень малое пробное тело. Закон обратной пропорциональности квадрату расстояния можно выразить математически простой общей формулой, которая позволяет рассчитать пространственную конфигурацию любого поля сил, обратно пропорциональных квадрату расстояния. Эта формула кажется простой для математиков и сложной для неспециалистов. Вот эта формула, которую мы приводим просто шутки ради:

d²V/dx² + d²V/dy² + d²V/dz² = 0

Символ V обозначает в ней разность потенциалов между данной точкой пространства и некоторым опорным нулевым уровнем, за который принимают потенциал земли, или точки, находящейся в бесконечности. Эта формула настолько важна, настолько универсальна, что для нее ввели даже сокращенную форму написания ²V = 0 (читается: набла квадрат V равно нулю). Написаны целые книги, посвященные решению конкретных задач с помощью этой формулы для точечных зарядов, заряженных шаров, цилиндров, тел неправильной формы, сложных конфигураций зарядов. Закон обратной пропорциональности квадрату расстояния применим, кроме того, к гравитационным полям, к задачам о распространении тепла путем теплопроводности, к задачам о течении воды и т. д., а также к магнитным полям (с существенными ограничениями). Таким образом, решения уравнения ²V = 0, которые дают картину электрического поля для некоторой конфигурации зарядов, позволяют также найти магнитное поле или картину течения воды при соответствующей конфигурации источников и стоков. Результаты измерений, проведенных для поля одного рода, можно перенести на поле другого рода. Например, какую-нибудь задачу о теплопроводности, важную для проектирования двигателя, может оказаться трудно исследовать экспериментально, но можно исследовать электрическое поле заряженных тел, которым придана такая форма, чтобы имитировать источник тепла. Между течением воды и электрическим полем как будто бы небольшая связь; в самом деле, реальной физической связи мало, а то и вовсе никакой, существует лишь некая формальная связь геометрического описания в том и другом случаях. Тем не менее, если обратиться к конфигурации течения в резервуаре с источником и стоком, представленной на фиг. 226 в гл. 9, то вы обнаружите картину электрического поля, созданного равными по величине положительным и отрицательным зарядами.

Это показывает, как одну и ту же математическую теорию можно применить к различным областям знаний. Мы не знаем, когда именно проявление закона обратной пропорциональности квадрату расстояния, изученное в какой-нибудь одной области физики, внезапно приобретет важное значение, и труды, в которых оно изложено, достанут с полки, чтобы использовать в другой области. Например, физики давно установили, что закон обратных квадратов должен быть применим к диффузии растворенных солей в жидкости — растворяющийся в кофе сахар распространяется вдоль линий тока, подобных линиям тока воды в озере; скорость диффузии связана с концентрацией соли «законом Фика», который на самом деле является частным случаем закона обратной пропорциональности квадрату расстояния. Много лет спустя исключительно важное значение приобрела задача о диффузии нейтронов в ядерном реакторе. К услугам физиков сразу же оказались закон Фика и множество готовых решений.

Картины поля и силы

Иногда творения кисти художника позволяют нам таинственным образом заглянуть в глубь его характера. Картины электрического поля точно так же позволяют сделать целый ряд выводов. Они должны дать вам возможность увидеть, как противоположные по знаку заряды цепко притягивают друг друга, а одноименные заряды отталкиваются, словно столкнувшись буферами, как взметаются вверх листочки электроскопа, как будто потянули за шнурок, которым поднимают шторы. Для Фарадея, размышлявшего над электрическими и магнитными полями столетие назад, эти силовые линии были в самом деле вполне реальными. Он представлял их себе в виде упругих трубок, каждая из которых начинается на положительном заряде, а заканчивается на равном ему по величине отрицательном заряде, развивает тянущее усилие вдоль своей оси и, раздаваясь в толщину, давит на соседние трубки. Такой образ мышления помогал Фарадею в его экспериментальных исследованиях и позволил ему подготовить базу, на которой зиждется электромагнитная теория света Максвелла. Мы и сейчас находим это представление полезным. Мы говорим даже о радиоволне как о колебании, распространяющемся вдоль силовой линии электрического поля, подобно волне, бегущей по веревке, хотя на самом деле это образное описание радиоволны вводит в заблуждение. Большинство ученых не мыслят категориями мистического «действия на расстоянии», мгновенно перекрывающего пустое пространство, отделяющее объект действия от источника действия, идет ли речь о силах тяготения или силах электрического притяжения. Вместо этого мы представляем себе, что воздействия переносятся полем (гравитационным или электрическим). Изменения, которые претерпевает сила, распространяются в виде изменений поля с определенной конечной скоростью.

Каждая силовая линия — это линия, вдоль которой маленький пробный заряд перемещается под действием электрического поля. В каждой точке силовой линии касательная к ней совпадает с направлением результирующей сил притяжения и отталкивания со стороны всех других зарядов, действующих на пробный заряд.

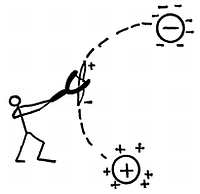
Фиг. 75. Исследование карты силовых линий электрического поля с помощью легкой стрелки, вращающейся на оси в центрах.

Можно наблюдать картины электрического поля (с помощью мелко настриженных волос в масле или маленькой стрелки, вращающейся в центрах) или найти конфигурацию поля геометрическим построением, используя утомительный способ векторного сложения сил, обратно пропорциональных квадрату расстояния, для нахождения направления результирующей. Можно также воспользоваться замысловатой смесью математического анализа и геометрии и рассчитать конфигурацию поля из уравнения . Все эти методы приводят, разумеется, к одному и тому же результату.

На фиг. 76 показаны картины электрического поля для некоторых случаев, а ниже даны пояснения к ним в духе представлений Фарадея.

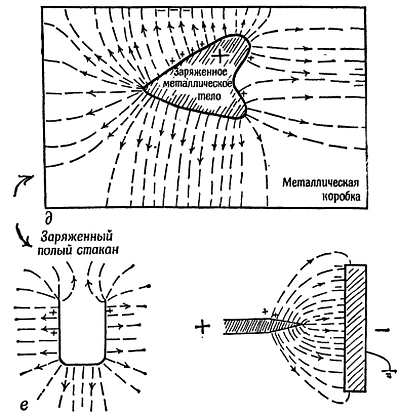
Фиг. 76. Картины электрических цепей

а) Силовые линии идут от положительного заряда к отрицательному. Они тянут разноименные заряды друг к другу. (Силовые линии натянуты, и это обусловливает взаимное притяжение зарядов.)

б) Силовые линии электрического поля в пространстве между двумя положительными зарядами расходятся друг от друга подобно вагонеткам, столкнувшимся буферами. Можно указать «нейтральную точку», в которой поля сил отталкивания обоих зарядов в точности гасят друг друга. (Силовые линии словно раздаются в толщину под действием давления и отталкиваются друг от друга в разные стороны; это обусловливает, или, можно по крайней мере сказать, иллюстрирует отталкивание.)

в) Силовые линии поля одиночного заряда представляют собой радиальные прямые, которые расходятся от заряда лучами, подобно силовым линиям гравитационного поля точечной массы или шара. (Чем дальше от заряда, тем меньше густота линий; это иллюстрирует ослабление поля с увеличением расстояния.)

г) Силовые линии поля, образованного любим заряженным куском металла, направлены перпендикулярно к поверхности. Они никогда не исходят от поверхности под другими углами. (Силовые линии поля покоящихся зарядов не могут быть наклонены к поверхности металла. В последнем случае они имели бы у поверхности составляющую, направленную вдоль поверхности; под действием этой составляющей вдоль поверхности происходило бы перемещение зарядов[52], на которых оканчиваются силовые линии, пока не установилось бы новое распределение зарядов, при котором силовые линии перпендикулярны к поверхности проводника.)

д) Силовые линии, исходящие от заряженного проводника неправильной формы, сгущаются вблизи любого выступа или острия; вблизи вогнутостей или полостей густота силовых линий уменьшается. (Вблизи острия силовые линии могут расходиться радиально в область, где их густота уменьшается; таким образом, боковое давление, которое силовые линии испытывают со стороны своих соседей, «сталкивает» их с ровных мест в область выступов. Это не очевидно, зато обратный эффект, связанный с полостями, легко себе представить: если бы силовые линии заходили внутрь полости, то они должны были бы «вытолкнуть» друг друга оттуда.)

е) Если силовые линии исходят от положительно заряженного острия, находящегося вблизи отрицательно заряженного плоского проводника, то они сгущены вокруг острия, где поле очень сильное, и расходятся в большую область вблизи плоскости, на которой оканчиваются, входя в плоскость перпендикулярно. Электрическое поле вблизи острия очень сильное. Оно может оказаться настолько сильным, что под его действием блуждающий электрон будет в состоянии бомбардировать молекулы воздуха и освобождать новые заряженные частицы — крошечные носители электричества. Первоначальный заряд на острие в этом случае притягивает вновь образованные носители зарядов противоположного знака. Притягиваясь к острию, они нейтрализуют часть находящегося на нем первоначального заряда. Носители заряда того же знака, что и заряд на острие, отталкиваются и стремительно уносятся прочь, увлекая за собой, благодаря столкновениям, молекулы воздуха и создавая «электрический ветер». Этот заряженный ветер используется для нанесения заряда на ленту в генераторе Ван-де-Граафа.

Электрический ветер можно использовать и для «собирания» заряда с заряженного предмета; в этом случае он служит для нейтрализации заряда противоположного знака. В конце этой книги вы встретитесь с применением сильного электрического поля, создаваемого острием заряженной иглы, для фотографирования атомов!

Фиг. 77. Действие заряженного острия в воздухе.

_{а — сильное электрическое поле вблизи острия вырывает электроны из нескольких атомов, оставляя атомы положительно заряженными. Как электроны, так и заряженные атомы совершают медленное перемещение в электрическом поле. Носители заряда противоположного знака движутся к острию и нейтрализуют часть находящегося на нем заряда. Носители одноименного заряда устремляются в направлении от острия, создавая «ветер», уносящий заряд.}

_{б — когда с помощью острия «собирают» заряд с какого-то источника, то ветер, идущий от острия, нейтрализует часть заряда источника, и острие приобретает соответствующий заряд. Этот метод можно применить для «собирания» заряда с движущихся тел (например, с ленты в генераторе Ван-де-Граафа), когда трущимся приспособлением для «собирания» заряда можно причинить какое-нибудь повреждение.} 

Еще более сильное поле может вызвать появление искр в воздухе вблизи острия или образование электронных лавин вокруг нити в счетчике Гейгера. Могут возникнуть даже гигантские вспышки между заряженными облаками и высоким деревом или верхом крыши. Заостренные металлические стержни, применяемые для защиты зданий, представляют собой молниеотводы, благодаря которым возникают слабые, невидимые и безвредные вспышки молнии, прежде чем разность потенциалов в электрическом поле между грозовым облаком и землей достигнет опасной величины. Но даже в случае большой вспышки молнии острие стержня служит местом, где разряд начинается раньше всего, и по стержню ток разряда отводится на землю, так что опасности не возникает.

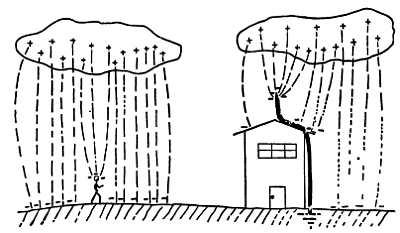
Фиг. 78. Грозовые облака часто несут огромные электрические заряды, возникающие, возможно, при раздроблении дождевых капель.

_{Они индуцируют заряды противоположного знака на крышах строений и поверхности Земли. Если поле системы заряженных тел становится достаточно сильным, чтобы вызвать образование заряженных носителей из молекул воздуха, то может возникнуть вспышка молнии. Воздух оказывается довольно хорошим проводником для начавшейся вспышки молнии, и может пройти колоссальный ток.}

Каждая силовая линия должна начинаться на положительном заряде и оканчиваться на отрицательном. Вспомните, что силовая линия указывает направление результирующей силы, действующей на малый положительный пробный заряд, и вы сразу согласитесь, что каждая силовая линия должна проходить именно так: от положительного заряда к отрицательному.

Отсюда следует, что сгущение силовых линий вблизи заряженной поверхности должно означать увеличение плотности заряда на поверхности. Если это так, то на поверхности металлического тела неправильной формы заряд должен распределяться неравномерно: плотность заряда должна быть наибольшей вблизи острых выступов и наименьшей во впадинах и вогнутостях. Мы уже проверили это предположение, поднося маленький заряженный пробный шарик или пластинку к электроскопу (фиг. 61).

ж) Электрическое поле в пространстве между параллельными заряженными пластинами однородно. Это поле удобно тем, что его напряженность можно рассчитать по показанию вольтметра. Мы будем пользоваться им при измерении постоянной , входящей в выражение закона Кулона, а позднее — при воспроизведении опыта Милликена, в котором измеряется заряд отдельного электрона. Постарайтесь представить себе картину этого поля, глядя на поле между двумя заряженными шарами и мысленно увеличивая диаметр шаров. Произведите в своем воображении экстраполяцию к предельному случаю бесконечно больших шаров (когда их поверхность плоская), между которыми по-прежнему остается малый воздушный промежуток. Но это лишь мысленные построения.

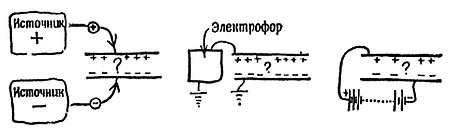
Фиг. 79. Заряжение параллельных пластин.

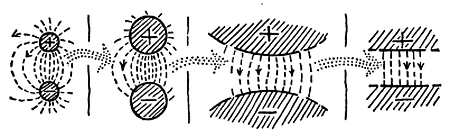
Фиг. 80. Экстраполяция.

Прибегнув к помощи алгебры или исследуя конфигурацию поля экспериментально, мы убеждаемся в том, что поле на самом деле такое, как показано на фиг. 81.

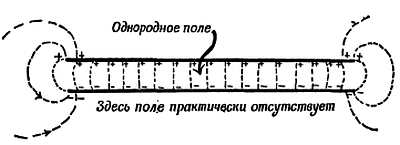
Фиг. 81.

В области между пластинами силовые линии представляют собой ряд параллельных и равноотстоящих прямых. (Интересно, что можно доказать математически с помощью уравнения , что если силовые линии параллельны друг другу, то они должны быть равноотстоящими прямыми.) Поле в этом случае всюду одинаково направлено и имеет одинаковую напряженность[53]: каким образом малый пробный заряд, помещенный между пластинами, смог бы узнать, где он находится среди леса параллельных силовых линий? Мы называем такое электрическое поле однородным. За пределами пластин поле практически отсутствует, если не считать областей вблизи краев пластин, где силовые линии выгибаются наружу (так называемый «краевой эффект»).

Пробный заряд величиной 1 кулон испытывал бы действие одинаковой силы в любой точке этого поля. Предположим, эта сила равна X ньютон. Значит, напряженность поля равна X ньютон на кулон. Давайте поручим некоему мифическому существу — демону протащить кулон от одной пластины до другой по силовой линии против электрической силы, действующей на кулон. Демону потребуется топливо, чтобы совершить работу, т. е. определенный запас энергии, которую он преобразует в потенциальную энергию кулона в электрическом поле. Демон должен прикладывать к переносимому кулону силу X ньютон на пути d м от одной пластины до другой. Он должен совершить работу при перемещении одного кулона, равную

СИЛА∙РАССТОЯНИЕ = (Х ньютон)∙(d м) = X∙d дж.

Но это не что иное, как энергия, сообщаемая одному кулону при прохождении от одной пластины до другой; это разность потенциалов, выраженная в джоулях на кулон, или вольтах. Следовательно, если вольтметр, подключенный к пластинам, показывает V в, то

X∙d дж/кулон = V в.

Отсюда

НАПРЯЖЕННОСТЬ напряженность поля X ньютон /кулон = V/d в/м

Таким образом, с помощью вольтметра и линейки можно измерить напряженность поля X; это оказывается удобным при проведении ряда важных опытов.

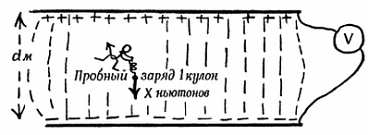
Фиг. 83. Xd ньютон-м/кулон = V дж/кулон.

Изоляторы и проводники

Опыты показывают, что заряженные тела, помещенные на подставку из сухого плексигласа, серы или эбонита, продолжают оставаться заряженными. Мы называем такие вещества изоляторами. По металлической проволоке, графиту, влажной нити и т. д. заряды могут перемещаться. Эти тела «проводят» положительные и отрицательные заряды друг к другу, в результате чего они нейтрализуются; при посредстве этих тел можно произвести перераспределение заряда между заряженными металлическим телом и каким-либо другим проводящим телом. Если последним является тело огромных размеров, такое, как Земля, то оно забирает столь большую долю заряда, что весь заряд первого тела исчезает. Мы называем тела, проводящие электричество, проводниками. Вода, будучи очень плохим проводником по сравнению с металлами, все же проводит заряды достаточно быстро, чтобы помешать целому ряду опытов. Некоторые изоляторы, в частности стекло, питают склонность к воде, и на них образуется пленка из молекул воды. Стеклянные стержни почти совершенно непригодны в качестве изоляторов для опытов по электростатике, если их специально не просушить.

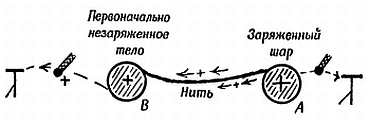
Фиг. 84. Демонстрация медленного движения заряда по влажной бечевке.

_{Для перенесения пробного заряда к каждому электроскопу служит маленький шарик. Заряд шара В увеличивается, а шар А теряет часть заряда.} 

Задача 9

«Стекло притягивает молекулы воды». Это известный вывод, к которому приводит изучение поверхностного натяжения. Какой способ экспериментальной проверки вы бы предложили для выбора изолятора, при работе с которым не возникало бы больших трудностей из-за его увлажнения?

Ток — это движение зарядов

Когда по проводнику движутся заряды по направлению к какому-либо заряженному телу или от него, мы говорим, что течет ток. Обнаружить действия тока (тепловое действие, химические эффекты, магнитное поле) можно, но они очень слабы[54]. Роуленд в 1876 г. проделал в этой связи замечательный опыт. Он раскрутил колесо, на обод которого были нанесены заряды, и наблюдал такое же магнитное поле, какое создал бы ток, текущий по ободу. Подключите в лаборатории батарею к пластинам очень большого «конденсатора» и отметьте с помощью измерительного прибора кратковременный импульс тока, связанного с движением зарядов к пластинам под действием батареи (опыт 7 гл. 41).

Вспомним теперь, как мы начали с заряжения тел от батареи, и вернемся снова к измерительным приборам и батареям, которыми пользуются в современной электротехнической лаборатории. Батареи являются источником статических зарядов, обладающих точно такими же свойствами, что и заряды, получаемые при натирании стержня. Кулоны зарядов Q₁ и Q₂, входящих в выражение закона Кулона, точно такие же, как кулоны, фигурирующие в соотношении «1 а = 1 кулон/сек». Они одинаковы по природе, и мы приравняем их по величине путем надлежащего выбора значения . (При экспериментальном определении значения  мы будем пользоваться для измерения напряженности электрического поля обычным вольтметром, градуированным в дж/кулон.) Отныне мы будем пользоваться полным набором нашего оборудования, измеряя напряжение либо вольтметром, либо электроскопом, и брать заряды с одинаковым успехом от электрофора, генератора Ван-де-Граафа, батареи или даже от сетевого источника питания с трансформатором и выпрямляющим диодом.

Модернизация представлений

Почему не пойти еще дальше в этой модернизации точки зрения и не излагать всю электростатику с помощью представления о свободных электронах? Просто потому, что ни один из экспериментов, рассмотренных до сих пор в этой главе, не обнаружил какого-либо явления, для описания которого необходимо привлечь электроны. Кроме того, существуют положительные заряды, в некоторых веществах движутся именно они.

Мы теперь знаем, что в металлических проводниках роль подвижных зарядов играют отрицательные электроны. Они могут свободно проходить через кусок металла, тогда как положительные заряды неподвижно закреплены в атомах твердого тела — металла. Таким образом, когда говорят, что «положительные заряды уходят по проволоке к земле», следовало бы сказать: «отрицательные заряды (электроны) идут по проволоке от земли и нейтрализуют положительные заряды у верхнего конца своего пути». Говоря: «шар, несущий положительные заряды», мы должны были бы сказать: «шар, с которого удалены отрицательные электроны». Когда говорят, что положительно заряженный шар, помещенный вблизи металлического стержня, «притягивает отрицательные заряды и отталкивает положительные заряды к другому концу стержня», следовало бы сказать: «притягивает отрицательные заряды, в то время как положительные заряды (нескомпенсированные) остаются у другого конца стержня».

В то же время в наших первых опытах ничуть не менее удобно считать, что движутся и положительные, и отрицательные заряды. В таком случае, поскольку неважно, движутся ли те и другие заряды или только отрицательные электроны, было бы антинаучно в этой связи настаивать на существовании какого-то различия. Тут вы сталкиваетесь с современной проблемой науки: хороша ли теория, которая удобна, непротиворечива и вполне подходит для объяснения рассматриваемого случая, или она должна быть, кроме того, истинной? Если вам сразу же необходимы настоящие электроны, то сформулируйте для себя с их помощью все прежние объяснения. Если вы приняли непреклонную позицию многих современных теоретиков, то придерживайтесь старой точки зрения, пока не столкнетесь со случаями, когда существенно, что «движутся только электроны». В необходимости ввести в рассмотрение электроны вы убедитесь дальше в этой книге; мы будем тогда пользоваться ими в полной мере.

Эбонитовый стержень отнимает электроны у меха, стеклянный стержень отдает их шелку. Мы знаем теперь, что любые два вещества, приведенные в соприкосновение друг с другом, обмениваются каким-то количеством электронов, причем одно приобретает добавочные электроны (приобретая тем самым отрицательный заряд), а другое теряет часть своих (становится положительно заряженным). Этот обмен электронами продолжается очень недолго после того, как оба тела приводятся в контакт. Обмен происходит до тех пор, пока не установится небольшая разность потенциалов (созданная разделенными при обмене положительными и отрицательными зарядами), которая препятствует дальнейшей миграции зарядов. При разобщении обоих тел механическое отделение одного тела от другого приводит к увеличению этой разности потенциалов, в результате чего разделенные заряды могут даже быть возвращены на место. Чтобы получить большой величины заряд «трением», необходим контакт между телами, причем дело тут не в трении, а в относительной скорости: быстро проведите шелком но стеклянному стержню, словно смахивая с него пыль, — не натирайте его.

Самый первый опыт по электростатике: притяжение мелких кусочков материала

Опыт, который проделывали древние греки, наблюдавшие притяжение мелких кусочков дерева и т, д. натертым янтарем, не так легко объяснить, как обычно полагают. Почему заряженное тело должно притягивать незаряженные кусочки материала? Потому что оно индуцирует в них заряды. Но тогда эти кусочки должны быть из металла, чтобы могло произойти разделение индуцированных зарядов.

В самом деле, легкие кусочки металла, например мелкие обрывки алюминиевой фольги, очень хорошо притягиваются заряженным стержнем, и объяснением этому служит взаимодействие с индуцированными зарядами. С кусочками идеального изолятора едва ли можно было бы наблюдать какой-нибудь эффект, но кусочки дерева или бумаги всегда обладают достаточной влажностью, которая делает их слегка проводящими. Если эти кусочки лежат на столе, связанном с землей, то «одноименный» наведенный заряд может уходить в землю, тогда притяжение будет еще сильнее. Это явление иллюстрирует фиг. 85.

Фиг. 85. Заряженный изолятор притягивает мелкие стружки металла.

На самом деле, однако, притягиваются даже идеальные изоляторы, хотя чаще всего слабо. По-видимому, заряды внутри молекул могут несколько смещаться в противоположные стороны, в результате чего молекулы становятся как бы электрически вытянутыми или поляризованными, и заряды на конце молекулы, ближайшем к поднесенному заряженному телу, притягиваются. Даже атом может быть поляризован, когда его электронное облако и ядро оттягиваются в противоположных направлениях. Именно так чаще всего притягивают друг друга атомы и молекулы при сближении; вандерваальсовы силы поверхностного натяжения — это электрические силы, обусловленные поляризацией молекул в полях своих соседей.

Фиг. 86. Поляризация молекулы.

Экспериментальное подтверждение закона обратной пропорциональности квадрату расстояния

Вместо измерения силы взаимодействия между двумя малыми зарядами закон обратной пропорциональности квадрату расстояния можно проверить косвенным, но не менее надежным путем, проделав удивительно простой решающий эксперимент. Если этот закон справедлив, то внутри пустой металлической коробки электрическое поле отсутствует, как бы сильно она ни была заряжена, и наоборот. Возьмите замкнутую металлическую коробку любой формы — цилиндрический стакан, полый шар, куб — и сообщите ей большой заряд. Затем выясните, что делается внутри коробки: есть ли там электрическое поле. Проверьте, если хотите, есть ли внутри коробки заряды, ибо там, где есть электрические заряды, должно быть и поле. Опыт показывает, что внутри коробки нет зарядов (если только не ввести внутрь дополнительные заряды с каким-либо предметом, укрепив его на изолирующей опоре) и нет электрического поля. Вам следует самим посмотреть, как проделывается этот опыт. Можно произвести его с небольшой полой металлической сферой и пробными шариками. А можно последовать примеру Фарадея, который забирался в большую проволочную клетку, предварительно заряженную. Несмотря на то что с внешней поверхности клетки вылетали искры, внутри не удавалось обнаружить никаких эффектов. Опыт простой и очевидный, но почему он подтверждает справедливость закона обратной пропорциональности квадрату расстояния?

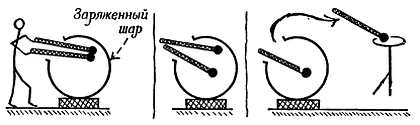
Фиг. 87. Проверка закона обратной пропорциональности квадрату расстояния.

Мы рассмотрим доказательство для полого шара, хотя его можно распространить на замкнутую проводящую коробку любой формы. Мы избрали геометрическое тело, которое служит символом совершенства, — им, как вы увидите, давно пользовался Ньютон для гравитационного варианта этой задачи. Предположим, что шар, показанный в разрезе на фиг. 88, заряжен положительно.

Фиг. 88. Электрическое поле внутри заряженного металлического шара.

Из соображений симметрии можно заключить, что заряд равномерно распределен по всей его поверхности. Допустим, что некий наблюдатель пытается обнаружить электрическое поле в точке D внутри шара. Он видит область Р₁ поверхности шара в пределах узкого конуса. Эта область несет заряд Q₁ который отталкивает положительный пробный заряд q наблюдателя в точке D. Если рассматривать заряд Q₁ то в точке D его поле отлично от нуля и направлено вдоль P₁D. Но, обернувшись назад, наблюдатель увидит противоположную область поверхности шара Р₂, заряд которой Q₂ тоже вносит вклад в поле в точке D, но действует на пробный заряд в противоположном направлении. Теперь наблюдатель определяет границы обеих областей более тщательно, построив конус с вершиной в D и основанием Р₁ и аналогичный конус с основанием Р₂. Можно показать, что действия зарядов Q₁ и Q₂ в точности гасят друг друга. Если наблюдатель в D ближе к Р₂, чем к Р₁, то площадь области Р₂ будет меньше и будет содержать меньший заряд. Значит, Q₂ меньше Q₁, и с этой точки зрения должен действовать на пробный заряд в точке D с меньшей силой. Но по закону обратной пропорциональности квадрату расстояния заряд Q₂, находящийся ближе, должен действовать на пробный заряд в точке D с большей силой, чем Q₁. Покажем, что оба фактора компенсируют друг друга. При равномерном распределении заряда по всей сфере — это обусловлено симметрией — заряд на одном квадратном сантиметре поверхности сферы будет всюду одинаков; заряд, приходящийся на два квадратных сантиметра, будет вдвое больше и т. д. Заряды областей Р₁ и Р₂ будут пропорциональны их площадям. Поскольку обе области выделены конусами с одинаковыми углами при вершине, их площади пропорциональны квадратам расстояний их от D[55]:

ПЛОЩАДЬ Р₁/ПЛОЩАДЬ Р₂ = d₁²/d₂² из геометрии.

Следовательно,

Q₁/Q₂ = d₁²/d₂²

Если закон Кулона справедлив, то следует ожидать, что силы, с которыми Q₁ и Q₂ действуют на очень малый пробный заряд q, равны ∙Q₁∙q/d₁² и ∙Q₂∙q/d₂². Но мы показали, что Q₁ и Q₂ пропорциональны d₁² и d₂². Поэтому запишем вместо Q₁ и Q₂ K∙d₁² и K∙d₂². Тогда силы, действующие на пробный заряд q, будут равны

∙(K∙d₁²)∙q/d₁² и — ∙(K∙d₂²)∙q/d₂²

или ∙K∙q и —∙K∙q, а эти силы равны и противоположны по направлению и, следовательно, взаимно уничтожаются. (См. ниже более краткий алгебраический вариант доказательства.)

Мы рассмотрели только пару узких конусов, выделяющих области Р₁ и Р₂. Можно представить себе еще одну пару конусов, примыкающих к первой и также проходящих через точку D. Те же самые рассуждения применимы к этой и ко всем другим парам конусов, которыми теперь можно мысленно заполнить весь шар[56].

Проверка

Если дан закон обратной пропорциональности квадрату расстояния, то можно показать, что «электрическое поле внутри полого заряженного шара отсутствует». При проверке закона обратной пропорциональности квадрату расстояния мы опираемся на обратное утверждение. Если некое утверждение верно, то обратное утверждение не всегда верно, но мы можем легко показать, что в данном случае оно верно. Геометрия конусов дает множители d₁² и d₂² в числителях приведенных выше выражений; в соответствии с законом обратной пропорциональности квадрату расстояний такие же множители оказываются в знаменателе каждой дроби. Один заряд больше другого, но эта разница компенсируется расстоянием в точно такой же пропорции. Если бы сила взаимодействия зарядов зависела от расстояния по какому-то другому закону и не подчинялась закону обратной пропорциональности квадрату расстояния, то в знаменателе каждой дроби были бы другие множители, и указанная выше компенсация нарушалась. Например, при обратной пропорциональности кубу расстояния действие большего по величине, но более удаленного заряда ослаблялось бы слишком сильно. (Так, если расстояния относятся, как 3:1, то площади вырезаемых областей относятся, как 9:1, и заряды на них, — как 9:1. Обратные квадраты расстояний относятся, как 1:9, и это компенсирует разную величину заряда. Обратные кубы расстояний относятся, как 1:27, и это нарушило бы компенсацию.)

Таким образом, если внутри равномерно заряженной сферы электрическое поле равно нулю, то сила взаимодействия между зарядами должна подчиняться закону обратной пропорциональности квадрату расстояния. Путем дополнительных геометрических построений, поразмыслив как следует над распределением зарядов на проводниках, можно обобщить этот вывод на замкнутую металлическую коробку любой формы. Если коробка отличается по форме от шара, то заряд распределяется на ее поверхности неравномерно. В самом деле, распределение заряда должно быть как раз таким, чтобы электрическое поле внутри всюду было равно нулю. Следовательно, мы располагаем простым и вместе с тем тонким методом проверки закона обратной пропорциональности квадрату расстояния: сообщить большой заряд замкнутой металлической сфере или коробке иной формы и проверить наличие полей. За пределами коробки электроскоп обнаруживает сильное электрическое поле, могут даже вылетать искры. Внутри коробки электрического поля, обусловленного внешними зарядами, нет.

Для более надежного обнаружения поля воспользуйтесь двумя маленькими шариками на изолирующих рукоятках. Поместите их незаряженными в исследуемую область. Коснитесь одним шариком другого, затем разведите их и проверьте на каждом наличие заряда (фиг. 87). Замкнутая металлическая коробка представляет собой идеальный экран для электрических сил (клетка из проволочной сетки почти так же хороша в этом отношении). Если она достаточно велика, то экспериментаторы могут спокойно работать в ней в условиях полной экранировки. Вы, наверное, замечали небольшие металлические экраны такого типа вокруг некоторых деталей вашего радиоприемника.

Приведенное подробное доказательство не нужно считать чем-то столь важным, что требуется помнить всю жизнь. Это характерный пример цепи научных рассуждений, ведущей от предположения о справедливости некоего закона к проведению его решающей проверки.

Алгебра

Приведем значительно более краткое и изящное доказательство. Предположим, что сила взаимодействия зарядов подчиняется степенному закону вида F ~ 1/d². Оба узких конуса вырезают на поверхности шара области с зарядами Q₁ и Q₂; Q₁/Q₂ = d₁²/d₂², исходя из геометрии и соображений симметрии. Обе области действуют на пробный заряд q с противоположно направленными силами F₁ и F₂, такими, что

F₁/F₂ = (Q₁/d₁ⁿ)/(Q₂/d₂ⁿ) = (Q₁/Q₂)/(d₂ⁿ/d₁ⁿ)

Если эти силы равны и противоположно направлены, то F₁/F₂ = 1 и (Q₁/Q₂)/(d₂ⁿ/d₁ⁿ) = 1. Следовательно, d₁ⁿ/d₂ⁿ  = d₁²/d₂² . Поэтому, чтобы силы взаимно уничтожались, должно быть n = 2.

ДЕМОНСТРАЦИОННЫЙ ОПЫТ

Измерение кулоновской постоянной

(Этот демонстрационный опыт сам по себе не имеет важного значения для данного курса, но он поможет вам понять опыт Милликена, в котором измеряется заряд электрона.) Мы воспользуемся плексигласовой подставкой с рычагом, применявшейся при проверке закона обратной пропорциональности квадрату расстояния (фиг. 69).

Чтобы измерить постоянную  в выражении F = ∙Q₁Q₂/d², нам нужно знать F, Q₁ и Q₂. Мы используем два одинаковых заряда (Q₁, Q₂) и измеряем силу F взаимодействия зарядов на измеренном расстоянии d между ними. Теперь мы знаем F и d в выражении F = ∙Q²/d², но не знаем Q. Чтобы найти Q, необходим отдельный опыт. Для такого Опыта можно воспользоваться установкой, представляющей собой сильно увеличенную модель прибора Милликена, с помощью которого он измерял заряд масляной капли (фиг. 89).

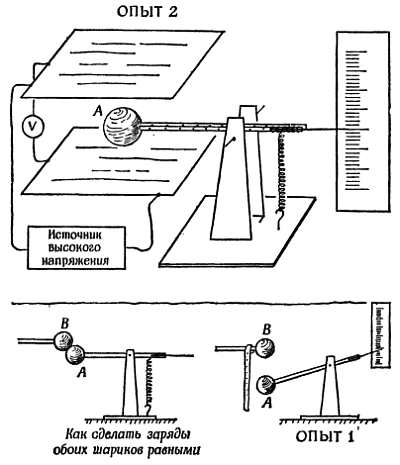
Фиг. 89. Измерение постоянной , входящей в формулу закона Кулона F = ∙Q₁Q₂/d²

Поместим шар А, который по-прежнему несет тот же самый заряд, в электрическое поле с известной напряженностью и измерим действующую на шар силу. Для этого оставим шар А на рычаге, уберем второй шар и расположим пару металлических пластин так, чтобы одна оказалась над шаром A, а другая под ним. (Верхняя пластина разрезана на две половины для удобства монтажа). Затем присоединим к пластинам зажимы источника высокого напряжения и подключим вольтметр, чтобы измерить напряжение. Далее мы определяем силу, приложенную к А со стороны однородного электрического поля. Зная напряженность поля X ньютон/кулон и новое значение силы F ньютон, можно вычислить заряд Q в кулонах. Но мы сделали так, чтобы заряды обоих шаров были одинаковы, следовательно, мы знаемоба Q в исходном соотношении и можем теперь вычислить .

Посмотрите, если удастся, этот демонстрационный опыт, он даст общее представление о том, как производятся важные с точки зрения науки измерения. Если вам не представится такой возможности, то проработайте предлагаемую задачу.

Задача 10. Опыт для измерения 

Используя приведенные ниже данные измерений, вычислите:

а) СИЛУ, приложенную к шару в опыте 2 (в ньютонах),

б) НАПРЯЖЕННОСТЬ ПОЛЯ между пластинами в опыте 2,

в) и отсюда ЗАРЯД, который несет шар А, в опыте 2,

г) СИЛУ отталкивания в опыте 1 (в ньютонах),

д) значение  (подставив вычисленное значение заряда и измеренное значение силы в опыте 1-е выражение закона обратной пропорциональности квадрату расстояния).

Данные измерений:

Калибровка рычага. В отсутствие зарядов стрелка рычага показывает нуль. Груз 1 Г (= 0,001 кГ), помещенный на шар А (незаряженный), перемещает стрелку с 0 до 56.

Опыт 1. Равные (неизвестные) заряды Q и Q' отстоят друг от друга на d = 0,10 м. После приближения второго заряда на указанное расстояние из бесконечности показание стрелки изменилось от 0 до 26.

Опыт 2. Заряд Q помещен в поле между двумя пластинами, отстоящими друг от друга на 0,40 м. После того как было создано электрическое поле (напряжение между пластинами при этом равнялось 16 000 в), стрелка, стоявшая на 0, стала показывать 16.

(Примечание. Поле нужно прикладывать, увеличивая его напряженность постепенно, а пластины следует перемещать так, чтобы шар А оказывался посредине между ними, иначе не удастся избежать ошибок вследствие «зеркальных зарядов», индуцируемых на пластинах зарядом шара.)

Индуцируемые заряды и потенциалы

Заряды легко перемещаются по проводникам. При этом не следует думать, что в металлической проволоке или каком-нибудь другом проводнике появится электрическое поле, если не подключить батарею, которая поддерживала бы непрерывное движение зарядов. Если в электрическое поле заряженного шара ввести незаряженный металлический стержень с закругленными торцами, в стержне сразу же происходит разделение зарядов и перемещение их вдоль поверхности. Перемещение зарядов будет происходить до тех пор, пока на всей поверхности стержня и во всех точках внутри него поле не станет равным нулю[57]. Тогда оказывается, что весь металлический стержень имеет один и тот же потенциал — разность потенциалов между различными частями стержня отсутствует, и ни в одной точке его нет электрического поля. Если бы существовали не равная нулю разность потенциалов между какими-нибудь двумя точками стержня или электрическое поле, то в металле текли бы токи до тех пор, пока разность потенциалов или электрическое поле не обратились бы в нуль.

Электрическое поле, равное нулю во всех точках металлического стержня, представляет собой результат сложения внешнего поля заряженного шара и поля, обусловленного зарядами на стержне.

Как только установится равновесие зарядов — это происходит очень быстро, — силы, приложенные к зарядам со стороны поля, будут направлены перпендикулярно поверхности металла и уже не смогут вызвать перемещения зарядов. Посмотрите на рисунки с изображением тел, наэлектризованных через влияние. Вы увидите, что в металлическом теле в одной его части могут находиться положительные заряды, в другой — отрицательные, в некоторых частях тело может быть не заряжено. Тем не менее все точки тела должны иметь один и тот же потенциал (т. е. разность потенциалов между любой точкой тела и землей должна быть одна и та же). Может показаться странным, что разность потенциалов между любыми частями равна нулю, хотя одна часть тела заряжена положительно, а другая — отрицательно. Но нужно помнить, что эти разнородные области, несущие положительные и отрицательные заряды и совсем незаряженные, существуют только из-за соседства других заряженных тел. Потенциал обусловлен совместным действием зарядов соседних тел и рассматриваемого тела.

Электростатическая индукция — интерпретация с помощью силовых линий

На фиг. 90 явление электростатической индукции иллюстрируется с помощью силовых линий. На фиг. 92 показано заряжение электроскопа через влияние. Это окончательные равновесные карты силовых линий.

Фиг. 90. Электризация через влияние.

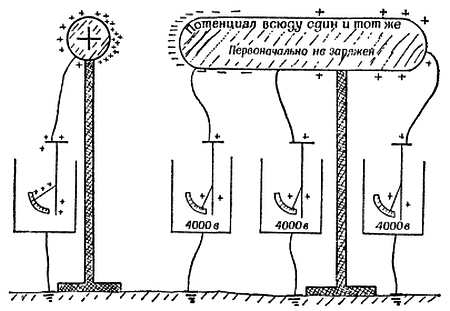
Фиг. 91. Что происходит, когда незаряженный металлический стержень подносят к заряженному шару?

_{Вольтметры показывают одну и ту же разность потенциалов между любой частью стержня и Землей. Следовательно, все части стержня находятся под одинаковым потенциалом, разность потенциалов между ними равна нулю. Обратите внимание на применение электроскопов в качестве вольтметров, не потребляющих тока.}

Фиг. 92. Стадии электризации электроскопа через влияние.

_{Заряженный стеклянный стержень индуцирует заряды на листочке и пр. Заряды, находящиеся на листочке, индуцируют заряды на металлическом корпусе, а поскольку корпус имеет соединение с землей, «одноименные» (отрицательные) заряды уходят с корпуса на землю.}

Фиг. 93. а — заряженное тело помещено в замкнутую металлическую коробку. Предполагается, что коробка соединена с землей, поэтому заряды на наружной поверхности не показаны; б — заряженный шар помещен в открытый маталлический стакан.

_{Вопрос: какова будет картина поля в каждом из трех показанных выше случаев, если шар смещен в боковом направлении и едва касается стенок коробки (стакана)?} 

Фарадеев цилиндр

Если тело с зарядом +Q поместить внутрь замкнутой металлической полости, то все силовые линии, идущие от +Q, должны кончаться на внутренней поверхности полости, на отрицательных зарядах, общая величина которых равна — Q. (Если бы силовые линии продолжались внутрь металла или проходили сквозь стенки полости, то существовали бы электрические поля и силы; они вызвали бы токи в металле, которые текли бы вплоть до установления равновесия зарядов.)

Высокий полый металлический цилиндр с открытым верхом ведет себя почти как замкнутая полость. Заряд +Q, внесенный внутрь цилиндра, индуцирует на внутренней поверхности цилиндра заряд — Q. На наружной поверхности распределяется равный ему по величине и противоположный по знаку заряд +Q, который уходит в землю, если цилиндр не изолирован.

Силовые линии в движении. Мгновенные токи (См. «моментальные снимки» на фиг. 94 и 95.)

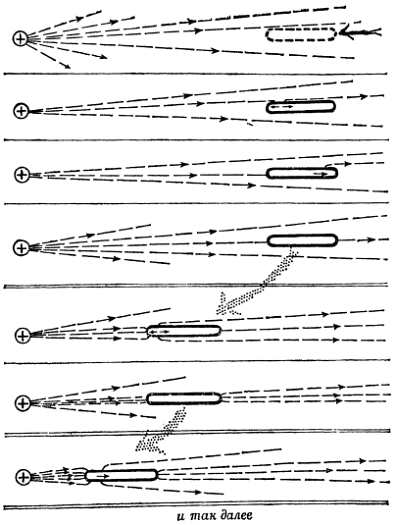
Фиг. 94. Движущиеся силовые линии.

_{Металлический стержень при приближении к заряженному шару нарушает картину электрического поля вокруг шара. Здесь показаны «моментальные снимки» конфигурации поля, на которых видны «оборванные» силовые линии в движении. Движущиеся концы силовых линий тянут заряды, заставляя их принять новое равновесное положение, и при этом текут токи. Силовые линии могут не быть перпендикулярны поверхности металлического стержня. Они должны быть наклонены к ней, должны иметь составляющую вдоль поверхности, в направлении которой на заряды действует сила. По мере приближения стержня к заряженному шару все новые силовые линии обрываются, и концы их тянутся вдоль стержня.}

_{«Моментальные снимки» показывают стадии, длящиеся лишь очень короткое время. Движущиеся концы силовых линий поля — это движущиеся заряды, перемещение которых представляет собой кратковременный ток. Эти токи действительно существуют, но скоро исчезают, — как только и экспериментатор и металлический стержень приобретают один и тот же потенциал (потенциал земли). Тогда в отсутствие разности потенциалов токов не будет.}

Фиг. 95. Прикоснувшись к стержню пальцем, индуцированному заряду дают «уйти на землю».

_{а — по мере приближения человека он отрывает все новые и новые силовые линии; б — «моментальный снимок»: силовые линии сокращаются, концы их подтягиваются, подводя заряды к пальцу человека; в — еще один «моментальный снимок»: последняя из исчезающих силовых линий поля.}

Силовые линии электрического поля вокруг изолированного заряженного шара представляют собой расходящиеся от шара радиальные прямые, идущие к зарядам противоположного знака, которые располагаются на удаленных стенах, потолке, земле. При приближении к шару металлического стержня последний, если можно так сказать, обрывает некоторые силовые линии. Оборванные силовые линии своими концами «прикрепляются» к зарядам, расположенным на поверхности стержня, и тянут их вдоль поверхности. Так, если шар заряжен положительно, то идущие от него оборванные силовые линии захватывают на стержне отрицательные заряды и увлекают их в сторону шара, а другие концы оборванных линий захватывают положительные заряды и тянут их в направлении от шара. По мере приближения стержня к шару разрывается все большее число линий, которые в соответствии с нашими представлениями разделяют в стержне бóльшие по величине индуцированные заряды.

Прикосновением пальца можно укоротить силовые линии, натянутые между металлическим стержнем и стенами. Правда, в переходный момент силовые линии могут даже удлиниться (если силовые линии идут к отрицательным зарядам на стоящем поблизости столе, то они, возможно, должны будут удлиниться, когда будут проходить через плечо экспериментатора). Но в конечном счете они сократятся до полного исчезновения, что на самом деле и происходит. Перед тем как вы поднести палец, силовые линии были протянуты от положительных зарядов на металлическом стержне к отрицательным зарядам на полу и на стенах. Когда вы коснетесь стержня пальцем, один конец силовой линии начинает тянуться к другому или оба конца — друг к другу (через палец, руку, тело, пол), пока концы силовой линии не встретятся и не произойдет их нейтрализация. (В металлах перемещаются отрицательные концы силовых линий и тянут за собой электроны.)

Батарея

Между зажимами батареи, не включенной в цепь, существует электрическое поле. Соедините зажимы проволокой, и поле будет стремиться исчезнуть; силовые линии поля, «стягивающие» зажимы батареи, будут тянуть заряды вдоль проволоки, создавая тем самым ток, который можно рассматривать как проявление непрекращающегося стремления избавиться от поля.

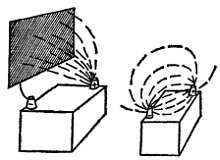
Фиг. 96. Батарея обладает собственным электрическим полем.

Силовые линии и движущиеся заряженные частицы

Силовые линии электрического поля указывают в каждой точке направление силы, действующей на малый пробный положительный заряд. Предположим, мы вносим в электрическое поле крошечную заряженную частицу. Будет ли она двигаться вдоль силовой линии? Оказывается, только вначале. Дело в том, что частица перемещается всегда в направлении ее результирующего количества движения. В любой точке частица при своем движении испытывает действие силы, направленной по касательной к силовой линии, и количество движения частицы в этом направлении увеличивается. Это приращение количества движения складывается с предшествующим количеством движения, которое может иметь другое направление, если силовые линии искривлены. Электроны, например, приобретают ускорение вдоль силовых линий электрического поля. Однако после того, как электроны начали двигаться, они не могут точно следовать направлению искривленных силовых линий, а уносятся в направлении вектора количества движения.

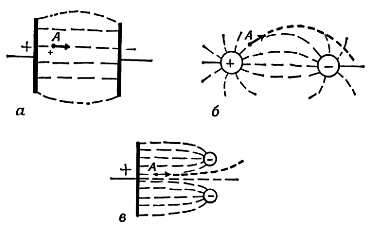
Фиг. 97. Движение маленькой положительно заряженной частицы, обладающей массой, в электрическом поле.

_{В каждом случае частица начинает двигаться из состояния покоя в точке А. Частица движется с ускорением, поскольку со стороны электрического поля к ней приложена сила, действующая на ее положительный заряд. Траектория частицы показана жирной пунктирной линией. (Отрицательная частица, например электрон, довершала бы такое движение при противоположном направлении поля.)}

_{На фигуре в показана частица в поле между положительной пластиной и двумя отрицательно заряженными стержнями, разделенными зазором. Траектория частицы не может сильно искривиться, и она проносится между стержнями.} 

Так электрические поля заставляют двигаться электроны: увлекают их от катода к аноду двухэлектродной радиолампы — диода, управляют потоком электронов в усилительной лампе — триоде, ускоряют пучок электронов в так называемой электронной пушке, создают периодическое горизонтальное движение электронного луча в пределах некоторого угла в осциллографической или телевизионной трубке. Попытайтесь представить себе картину электрических полей, которые увлекают электроны и управляют их движением в описываемых ниже приборах.

Электроны в электрическом поле

Если поместить в электрическое поле заряженную частицу, то на ней соберется несколько силовых линий поля, которые начнут тянуть частицу, как показано на фиг. 98, а. Электроны, обладающие отрицательным зарядом, движутся под действием силы, направленной противоположно полю[58], как показано на фиг. 98, б. Разумеется, электрическое поле, действующее на электрон (фиг. 98, в), не претерпевает изменений из-за присутствия электрона, который не искажает общей картины поля. Стрелка на фиг. 98, в указывает направление силы, приложенной к отрицательному электрону, находящемуся в электрическом поле.

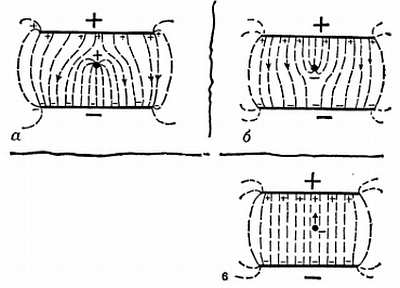
Фиг. 98. Заряженное тело малых размеров в электрическом поле.

_{а и б — результирующее поле; в — заряд тела слишком мал, чтобы искажать однородное поле. Фигура в изображает также внешнее поле, которое действует на заряд тела во всех случаях независимо от того, велик заряд или мал.}

_{Стрелка указывает направление силы, действующей на отрицательный заряд.}

Испускание электронов накаленными металлами

Опыты с простыми радиолампами показывают, что раскаленная нить накала служит источником некоего переносчика тока, способного поддерживать ток в одном направлении — от нити накала к аноду. Это имеет место даже в том случае, если в лампе создан самый высокий вакуум — идеальный изолятор, разделяющий нить накала и анод. Поскольку ток есть движение зарядов, в лампе должны появляться какие-то носители тока, обладающие электрическим зарядом. При холодной нити никакого тока нет: эффект прохождения тока наблюдается только, когда нить раскалена. Таким образом, мы приходим к предположению, что носители тока испускаются нитью. Миллиамперметр и вольтметр говорят нам, что если эти носители перемещаются от нити накала к аноду, то они должны обладать отрицательным зарядом. Ток через лампу условно рассматривается как ток положительных зарядов, текущий от анода к нити накала, направление этого тока считается положительным; говорят также об отрицательном токе в направлении от нити накала к аноду. Разность потенциалов, обусловливающая этот ток, приложена так, что анод положителен, а нить накала отрицательна. Поэтому электрическое поле притягивает отрицательные заряды от нити накала к аноду. Если изменить направление приложенной разности потенциалов, то никакого тока не будет, носители будут испытывать действие силы, направленной в сторону нити накала, и не смогут двигаться. Мы называем эти носители тока отрицательными электронами или просто электронами.

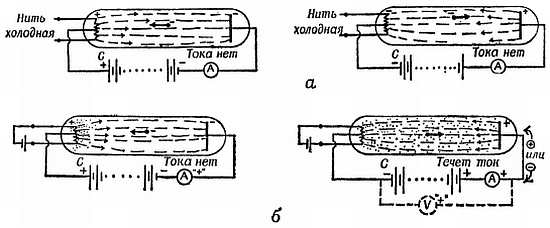
Фиг. 100. Простейшая радиолампа.

_{а — когда нить накала холодная, тока нет (если только к лампе не приложена очень большая разность потенциалов, под действием которой вырываются электроны из «холодных» атомов).}

_{б — при таком включении батареи, как показывает вольтметр, анод положителен, а катод отрицателен. Миллиамперметр показывает, что через лампу течет положительный ток в направлении <— (или отрицательный ток в направлении —>).}

Фиг. 101. Если окошко из тонкого листового вольфрама, впаянное в торец стеклянной трубки, достаточно сильно нагреть пламенем газовой горелки, то через трубку под действием подходящего электрического поля будет проходить поток электронов.

По-видимому, в раскаленной металлической нити накала есть свободные электроны, которые движутся с большой скоростью и могут вылетать за пределы нити, подобно молекулам, испаряющимся из жидкости. Электроны способны вырваться из металла только в том случае, если соседние атомы смогут сообщить им достаточное количество добавочной энергии, когда металл достаточно нагрет. Чтобы заставить металл испускать электроны, необязательно нагревать его электрическим током. Полоска листового вольфрама, если нагреть ее в пламени небольшой газовой горелки, будет точно так же испускать электроны. Во многих современных радиолампах применяется так называемый косвенный подогрев. В этом случае накаленный поверхностный слой, который испускает электроны, — катод[59] разогревается маленьким электрическим подогревателем, находящимся в непосредственной близости к нему. Обычно катод имеет вид трубки, внутри которой проходит проволочный подогреватель. Катод часто покрывают слоем особого состава из смеси окислов, благодаря которому электроны интенсивно испаряются при сравнительно низкой температуре.

Мы будем в дальнейшем изображать радиолампы с отдельным катодом К и подогревателем НН.

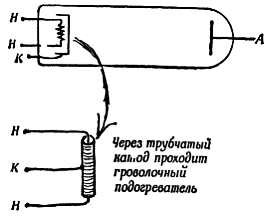
Фиг. 102. Радиолампа с отдельными катодом и подогревателем.

Фиг. 103. Схематическое изображение двухэлектродной радиолампы.

РАДИОЛАМПЫ

Диод и его применение для выпрямления тока

Электроны, испаряющиеся из накаленного катода, движутся под действием электрического поля в пространстве между катодом и анодом. Они ускоряются и налетают на анод, передавая ему свою кинетическую энергию и усиливая хаотические колебания атомов материала анода, в результате чего анод нагревается.

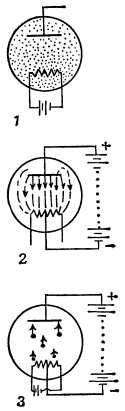
Фиг. 104. Простейшая радиолампа (диод).

_{Внутри баллона создан высокий вакуум.}

_{1 — если нагреть вольфрамовую нить накала до белого каления, то электроны интенсивно испаряются из нее и образуют внутри баллона своего рода облако. Электронное облако, если оно сохраняется, создает тормозящее электрическое поле, которое противодействует дальнейшему испарению электронов.}

_{2 — батарея, присоединенная к нити накала и к аноду, создает между ними электрическое поле. Поле, показанное на фигуре, заставляло бы положительный заряд двигаться от анода к нити накала; в действительности под действием этого поля отрицательный заряд перемещается от нити накала к аноду.}

_{3 — при накаленной нити и приложенном поле поток электронов движется через лампу к аноду. Если изменить направление поля на обратное, то электроны отталкиваются назад, и тока в лампе нет. Если увеличивать приложенное поле, то поток электронов достигает максимума, когда все электроны, испаряющиеся с катода, попадают на анод.}

Лампа, в которой создан хороший вакуум, наполняется облаком электронов, подобно молекулам насыщенного пара. Если между катодом и анодом лампы приложить электрическое поле соответствующей величины и направления, то электронное облако будет перемещаться к аноду, и пойдет ток. Облако электронов ослабляет поле; некоторые электроны отталкиваются отрицательным зарядом облака назад, к катоду, поэтому ток через лампу мал.

Только приложив очень большое напряжение, мы получим максимальный ток, когда все электроны проносятся в направлении анода по мере их «испарения». Если теперь приложить еще большее напряжение, то увеличить ток уже не удастся. Этот неизменный максимальный ток называется током насыщения. (Смысл слова «насыщение» здесь, к сожалению, расходится со значением этого слова в выражении «насыщенный пар». Понятие «ток насыщения» вызывает представление о том, как молекулы пара уносятся сильным ветром сразу же после испарения — мечта хозяйки, которой приходится сушить белье.)

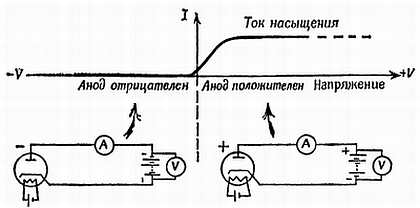
Фиг. 105. «Характеристика» диода: график зависимости тока от напряжения.

_{Обратите внимание на то, что I — это отрицательный ток, идущий от катода к аноду.}

Электроны в диоде могут пересекать пространство между катодом и анодом только в одном направлении — от катода к аноду. Таким образом, лампа действует как вентиль, легко пропуская ток, когда анод положителен, и не пропуская тока при обратной разности потенциалов, приложенной к электродам лампы. Это свойство диода используют в тех случаях, когда требуется получить прямой (постоянный по направлению) ток от источника переменного тока. Сеть коммунального электроснабжения дает переменный ток, пригодный для освещения и работы нагревательных приборов и специально сконструированных электромоторов, но совершенно непригодный для зарядки аккумуляторов или высоковольтного питания усилительных ламп в радиоприемнике.

Задача 11. Зарядка аккумуляторов

На фиг. 106 показан диод, у которого катод подогревается током от 6-вольтового аккумулятора. Диод используется для зарядки 18-вольтовой аккумуляторной батареи (три автомобильных аккумулятора, соединенных последовательно) от источника переменного тока. Срисуйте все изображенные на фигуре приборы и дополните схему необходимыми для ее работы соединениями.

Примечание. Чтобы зарядить аккумулятор, ток (имеется в виду положительный ток, совпадающий по направлению с условным током положительных зярядов) должен входить в его положительный зажим, проходить через аккумулятор и выходить из отрицательного зажима; если рассматривать ток отрицательных зарядов (отрицательный ток), то он, разумеется, должен проходить в противоположном направлении.

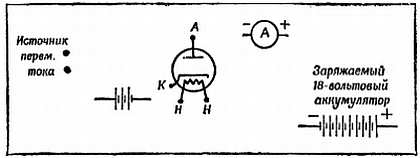
Фиг. 106. К задаче 11.

Схему выпрямления тока, элементы которой показаны на фиг. 106, можно усовершенствовать, используя два диода. Если приложить между катодом и анодом диода переменное напряжение, то в цепи появятся импульсы тока одного направления (по одному импульсу на каждый период), чередующиеся с интервалами, когда ток отсутствует. Схема выпрямления, в которой используются два диода, дает вдвое больше импульсов тока, два за каждый период. Пульсирующим током, который дают обе схемы, можно заряжать аккумулятор. Можно сгладить этот ток с помощью дросселя и конденсатора и получить постоянное по амплитуде напряжение, необходимое для работы радиоламп. Описанное получение постоянного тока из переменного, как уже говорилось, носит название выпрямления, поскольку ток после выпрямления не меняет своего направления и течет лишь в прямом направлении. Обязательно посмотрите, как происходит выпрямление переменного тока, на экране осциллографа.

Трехэлектродная лампа

Простой диод можно превратить в еще более полезный электровакуумный прибор, если ввести в него третий дополнительный электрод с отверстиями — сетку, которую располагают вблизи катода, чтобы усиливать или ослаблять поток электронов, направленный к аноду. Это трехэлектродная лампа, или триод, — основная лампа, используемая в радиоприемниках; она может служить для усиления электрических напряжений и токов и выпрямления тока. (Есть еще более сложные радиолампы; они содержат например, дополнительные сетки для захвата рассеянных электронов, но это, так сказать, украшения к основной лампе-триоду. Кстати, те же самые задачи, притом с меньшими хлопотами, могут быть решены с помощью транзистора.)

Фиг. 107. Триод.

_{Схематическое устройство трехэлектродной радиолампы — триода, имеющей нить накала, анод и сетку. Небольшая, обычно тормозящая разность потенциалов между нитью накала и сеткой сильно влияет на поток электронов, вылетающих из нити, давая возможность легко управлять им. Многие электроны проходят сквозь ячейки сетки, и за пределами сетки ускоряющее поле увлекает их к аноду.} 

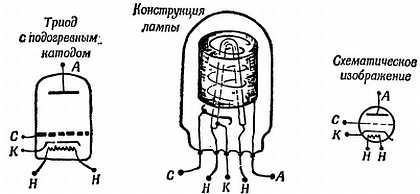
Фиг. 108. Триод.

Триод как усилитель

Между катодом и сеткой прикладывают небольшое напряжение, «сигнал», который нужно усилить. Анод поддерживается под высоким напряжением неизменной величины по отношению к катоду. Это напряжение создает сильное электрическое поле за пределами сетки, стремящееся оттянуть электроны к аноду. В триоде небольшое изменение напряжения между сеткой и катодом очень сильно влияет на поток электронов, летящих к аноду: на этом основано усилительное действие лампы.

Если сетка оказывается положительной по отношению к катоду, то электроны сразу же попадают в ускоряющее поле. Сетка притягивает электроны из облака, окружающего катод, они устремляются к сетке, приобретая дополнительное количество движения. При этом траектории большей части электронов не совпадают с искривленными силовыми линиями поля, идущими к сетке, и электроны проносятся сквозь сетку. За пределами сетки электроны захватываются ускоряющим полем и мчатся к аноду. Триод становится подобным диоду в режиме насыщения. Этот тяжелый режим, когда сетка положительна, используется редко: обычно сетка находится при отрицательном потенциале по отношению к катоду.

Если сетка отрицательна, то картина получается иной; этот режим работы лампы имеет гораздо большее практическое значение. Отрицательная сетка сдерживает электронное облако. Некоторые электроны просачиваются сквозь ячейки сетки и устремляются к аноду под действием сильного поля за пределами сетки. Если же сетка лишь слегка отрицательна по отношению к катоду, то часть силовых линий поля, идущих от анода, проходит через сетку и закрепляется на электронах. В этом случае электроны, испытывая небольшое притяжение, медленно перемещаются от катода к сетке, а пройдя сквозь сетку, устремляются к аноду. Поток электронов в промежутке катод — сетка сильно зависит от разности потенциалов между сеткой и катодом, и с помощью нее очень легко управлять этим потоком. Малые изменения напряжения между сеткой и катодом сильно влияют на поток электронов, покидающих катод, и тем самым на анодный ток. Это очень удобный способ управлять потоком электронов с помощью малого напряжения. Чтобы достичь такого же изменения потока электронов путем изменения напряжения между катодом и анодом, это последнее пришлось бы изменить много больше. Иначе говоря, триод позволяет увеличивать (усиливать) напряжение.

Более того, триод усиливает мощность. К сетке и от нее текут лишь очень малые токи: большая часть электронов направляется к аноду. Таким образом, в цепь сетки триода под действием малого напряжения поступает чрезвычайно малый ток, в то время как в анодной цепи появляется гораздо больший ток, который, протекая через достаточно большое сопротивление, вызывает большие изменения напряжения. Другими словами, триод отдает в анодную цепь значительно большую мощность и вызывает значительно большие изменения мощности, чем подводятся к сетке. Триод напоминает в этом отношении современную машину-автомат, в которой с помощью легкого нажатия кнопки управляют огромными количествами энергии. В управлении потоком энергии состоит основная функция триода как усилителя. Дополнительная энергия поступает от источника высокого постоянного напряжения (это может быть батарея или сетевой выпрямитель), который включают в анодную цепь.

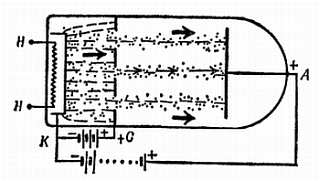
Фиг. 109. Электрическое поле в триоде при положительной сетке (ненормальный режим).

_{Сквозь сетку проходит мощный поток электронов, стремительно уносимых полем к аноду; некоторые электроны задерживаются сеткой С. Тонкие стрелки показывают скорости электронов. Толстые стрелки указывают направление силы, действующей на отрицательные электроны со стороны поля.} 

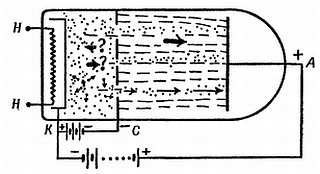
Фиг. 110. Электрическое поле в триоде при отрицательной сетке (обычный режим работы лампы),

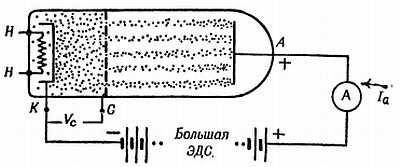
Фиг. 111. Триод в действии.

_{Электроны, испускаемые накаленным катодом, образуют облако в области между катодом и сеткой. Электроны, которым удается пройти сквозь ячейки сетки, движутся под действием сильного поля к аноду. Разность потенциалов между сеткой и катодом управляет потоком электронов.} 

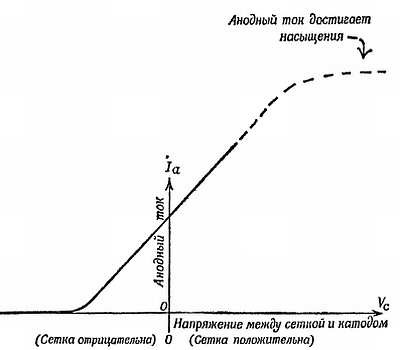
Фиг. 112. «Характеристика» триода.

_{Напряжение анода поддерживается при снятии этой «характеристики» постоянным.}

Триоды в радиоприемниках

В усилителе радиоприемника приходящие радиосигналы создают малые напряжения между катодом и сеткой триода[60]. Возникающие в результате этого изменения потока электронов, направляющихся к аноду, вызывают большие изменения напряжения между концами так называемого «сопротивления нагрузки», включенного в анодную цепь, с которого «снимают» эти изменения напряжения. Напряжение на сопротивлении нагрузки можно приложить между сеткой и катодом еще одного триода для дальнейшего усиления и в конечном счете заставить работать от этого напряжения динамик.

Чтобы динамик приемника мог работать от радиосигналов, их нужно не только усилить, но и выпрямить — пропустить через какое-то устройство, дающее на выходе ток одного направления. Необходимость выпрямления радиосигналов не очевидна; почему их приходится выпрямлять, будет рассказано в гл. 41.

Триод может работать как выпрямитель у нижнего излома своей характеристики — графика зависимости тока от напряжения, где характеристика загибается, приближаясь к горизонтальной оси. Однако, несмотря на возможность использовать одну и ту же лампу как для выпрямления, так и для усиления, лучше разделить обе эти задачи и применять разные лампы.

Триоды сочетают усилительные свойства с достоинствами диодов. Диоды находят применение в «источниках питания» для получения постоянного тока из переменного; эти источники используются вместо батарей. Обеим лампам угрожает конкуренция со стороны новых приборов — маленьких «транзисторов», в которых нет накаливаемых элементов. В транзисторе в кусочке полупроводникового кристалла создается однонаправленное управляемое противодействие движению электронов на стыках полупроводниковых материалов двух типов в одном и том же кристалле.

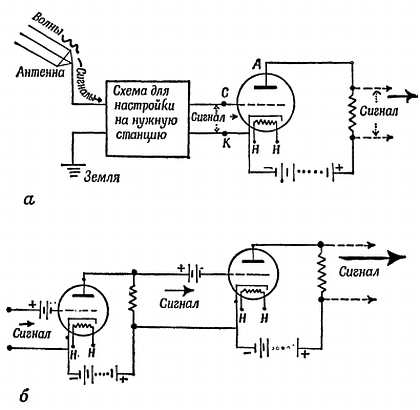
Фиг. 113. Усиление радиосигналов.

_{а — усиление на одном триоде; б — две ступени усиления.} 

Электронная пушка

Тут вы оказываетесь похожим на человека, который всю жизнь говорил прозой, сам того не зная. Вы, должно быть, имели дело с электронной пушкой, не зная об этом. Электроны, испаряющиеся из накаленного катода, ускоряются под действием электрического поля и бомбардируют анод. Если в аноде проделать отверстия, то через каждое отверстие будет выбрасываться поток электронов. Электроны продолжают свой путь, пока не ударятся о стенки баллона или, если в лампе есть остатки газа, пока не потеряют энергию при столкновениях с молекулами газа. Если электроны обладают достаточно большой энергией, то они могут пройти даже сквозь тонкие стеклянные или металлические стенки баллона и вылететь в атмосферу, где вскоре тормозятся.

Электронная пушка, предназначенная для получения узкого пучка электронов, обладает некоторыми дополнительными особенностями устройства. Анод имеет лишь одно отверстие, добавлены сетки для управления фокусировкой и интенсивностью пучка. Благодаря фокусировке электроны выходят очень узким пучком или собираются в маленькое пятнышко к моменту достижения мишени, если пучок при выходе расходящийся. Чтобы добиться этого, создают небольшие дополнительные электрические поля. Проблемы, связанные с получением полей нужной конфигурации, составляют новую область техники — «электронную оптику», в которой пользуются плодотворной аналогией между классической оптикой и механикой электронов.

Интенсивностью пучка электронов управляют посредством отрицательно заряженной сетки, которая расположена вблизи нити накала и создает поле, тормозящее поток электронов. Сетка таким образом управляет числом электронов, которые достигают ускоряющего поля. Если сетка находится под большим отрицательным потенциалом, она отталкивает все электроны обратно к нити накала. Если сетка слегка отрицательна по отношению к катоду, то она позволяет осуществить эффективное управление потоком электронов. При положительной сетке плотность потока максимальна, и пушкой уже нельзя управлять. На схемах мы будем изображать такие электронные пушки без дополнительных сеток или анодов.

В ранний период изучения электронов, на пороге 1900 г., таких обильных источников потока электронов не было. Вместо них Дж. Дж. Томсону и другим исследователям пришлось пользоваться электронами, которые были вырваны из металлов или выбиты из молекул разреженного газа в разрядных трубках, а затем ускорены в трубке под действием разности потенциалов в несколько тысяч вольт. Это давало слабый пучок электронов с неодинаковой кинетической энергией.

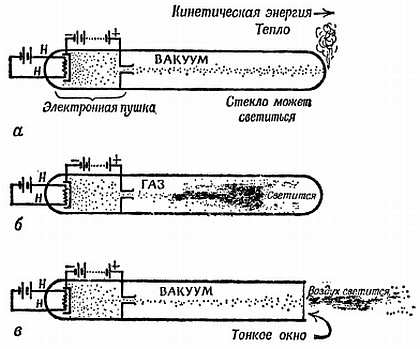
Фиг. 114. Электронные пушки.

_{а — трубка, в которой создан вакуум; б — трубка с небольшим количеством газа; в — трубка, в которой создан вакуум; электроны выходят наружу через очень тол кое металлическое окно в торце трубки.} 

Осциллографы

Пучок электронов, вылетающих из электронной пушки, если его путь проходит через вакуум и он не встречает больше электрических полей, имеет вид прямой линии, а скорость электронов не меняется. Налетая на торцевую стенку стеклянного баллона, электроны останавливаются, их кинетическая энергия переходит в тепло, за исключением тех редких случаев, когда вместо этого при торможении электрона испускается фотон (квант) рентгеновского излучения. Если покрыть стекло слоем специального флуоресцирующего состава, то в том месте, куда ударяются электроны, появится светящееся пятно. Налетающие электроны вызывают свечение не в результате нагрева, а благодаря возбуждению электронов в атомах покрытия. Этим светящимся пятном можно чертить графики и рисовать изображения. Электрические поля отклоняют пучок справа налево и слева направо в горизонтальном направлении или вверх и вниз, заставляя его вычерчивать графики или рисовать изображения на телевизионном экране. Электроны в пучке движутся очень быстро и обладают ничтожно малой массой, поэтому пучок невероятно быстро и легко реагирует на действие отклоняющих полей.

На фиг. 115 показана трубка электронно-лучевого осциллографа — предшественница телевизионных трубок.

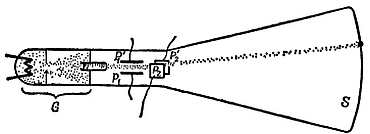
Фиг. 115. Трубка электронно-лучевого осциллографа.

Электроны вылетают узким пучком из пушки G и налетают на экран S, расположенный на противоположном конце трубки. Экран S покрыт слоем вещества, которое светится при бомбардировке электронами. Пучок фокусируется пушкой в маленькое светящееся пятно на экране. Проходя через отклоняющее электрическое поле, созданное между пластинами Р₁ и Р'₁, пучок смещается вверх или вниз, так как электроны получают некоторое количество движения в вертикальном направлении. Имеется еще одна пара пластин, Р₂ и Р'₂, между которыми создают поле для отклонения пучка в горизонтальной плоскости. Если к пластинам Р₁ и Р'₁ подключить батарею (с э.д.с. скажем, 45 в) так, чтобы верхняя пластина стала положительной, то пучок отклонится вверх, и пятно будет находиться в определенном положении в верхней части экрана S, пока подсоединена батарея[61]. Если к пластинам Р₁ и Р'₁ подвести переменное напряжение, то пятно будет перемещаться вверх и вниз, практически мгновенно следуя за изменениями напряжения. Чтобы вычертить графическую картину изменения вертикального отклонения во времени, горизонтальное электрическое поле должно перемещать пучок с постоянной скоростью по экрану трубки в горизонтальной плоскости. Схема такой «развертки» рассмотрена в задаче 11 гл. 36. Вам следовало бы поработать с трубкой в лаборатории (опыт 10 гл. 41).

В телевизионной трубке пятно должно совершать периодическое перемещение вверх и вниз и справа налево, быстро покрывая всю площадь кадра. Одновременно с этим перемещением пятна по экрану его яркость должна изменяться под действием приходящих радиоволн, благодаря этому получаются светлые и темные части изображения.

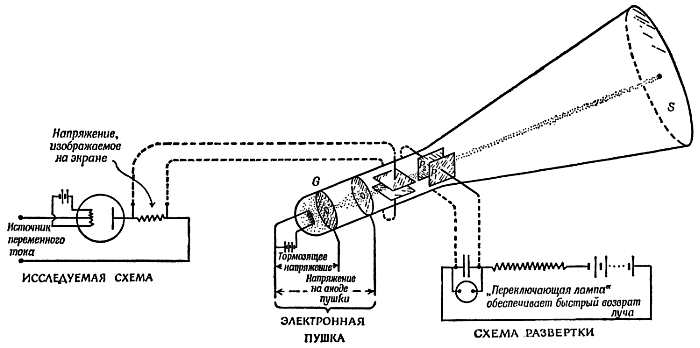
Фиг. 116. Схема с простой электронно-лучевой трубкой для вычерчивания графической картины изменения тока во времени.

_{Разность потенциалов на сопротивлении, пропорциональная току в цепи, прикладывается к пластинам трубки и создает вертикальное отклоняющее электрическое поле. «Переключающая лампа» в цепи развертки представляет собой специальную газонаполненную радиолампу, подобную неоновой газосветной лампе. При низком напряжении эта лампа не проводит тока. Когда напряжение на ней достигает определенной величины, лампа внезапно вспыхивает, и через нее проходит ток (благодаря образованию ионов при столкновениях). Ток, проходящий через высокое сопротивление, заряжает конденсатор. Когда конденсатор зарядится до определенного напряжения, лампа вспыхивает, давая возможность конденсатору быстро разрядиться до нулевого напряжения. Таким путем получают пилообразное напряжение, необходимое для развертки.}

Задача 12

Предположим, вы располагаете электронной пушкой типовой конструкции и вас попросили спроектировать телевизионную трубку. Как бы вы предложили осуществить изменение яркости пятна? (Существует несколько схем, некоторые из них можно использовать не только в телевизионной трубке.)

Указание. Электроны, которые ударяются об экран, должны обладать максимальной скоростью пучка, иначе они вообще не смогут возбудить свечение.

В современных телевизионных трубках отклонение электронного пучка осуществляется не электрическими, а магнитными полями. Вскоре вы увидите, что их можно использовать вместо электрических полей.

Энергия электрического поля. Волны

[Оставшаяся часть этой главы описывает необыкновенные явления, находящие полное объяснение и подтверждение при более серьезном изучении, чем то, которое предлагается здесь. Тем не менее она проливает некоторый свет на понятие электрической энергии и дает представление об электромагнитных волнах.]

Движущиеся заряды переносят с собой создаваемые ими поля, силовые линии поля движутся вместе с зарядами, подобно тому, как пышные усы — вместе с их обладателем. Во всем пространстве вокруг проводов электрической цепи, по которым течет ток, должны перемещаться силовые линии[62]. Именно эти движущиеся силовые линии переносят электрическую энергию от батареи к различным частям цепи через разделяющее их пространство. Силовые линии натягиваются и тянут заряды, поддерживая ток, и передают энергию своей упругой деформации, почти как движущийся приводной ремень.

Это движение сопровождается новым эффектом: появлением магнитного поля, у которого также есть силовые линии (силовые линии совсем иного рода, хотя и с похожей конфигурацией). Магнитное поле, связанное с протеканием тока по цепи, обладает, оказывается, собственным запасом энергии, количество которой пропорционально величине (сила тока)². Сходство с кинетической энергией, которая пропорциональна величине (скорость)², наводит на мысль, что энергию магнитного поля можно рассматривать как кинетическую энергию цепи, связанную, возможно, с кинетической энергией движения электронов. Эта «кинетическая энергия» магнитного поля тока дает основание считать, что оно обладает чем-то подобным массе. А потенциальная энергия, присущая электрическим полям, позволяет провести аналогию между их поведением и поведением пружины или растягиваемого шнура. В действительности между обоими видами поля существует взаимосвязь. Вместе взятые они образуют электромагнитное поле, обладающее как «пружинистостью», так и инертностью, или массой. Мы знаем, что в любой среде, которая характеризуется упругостью и массой, могут распространяться волны: вдоль натянутой веревки, вдоль массивной витой пружины, в воздухе — в виде звуковых волн. Таким образом, мы можем высказать смелую догадку и предположить, что в электромагнитном поле могут распространяться волны. И действительно, можно заставить электрическую цепь посылать волны, если быстро изменять текущий по ней ток. Это те самые радиоволны, существование которых столетие назад предсказал Максвелл. Вывод Максвелла представлял собой не просто догадку, а был основан на его математической формулировке законов электрического и магнитного полей.

Электромагнитные волны

В тех случаях, когда ток в цепи быстро меняется и заряды не просто движутся, но движутся с ускорением и замедлением, должны происходить изменения полей. Эти изменения, как мы теперь знаем, распространяются не мгновенно — информация о них достигает удаленных от цепи областей пространства лишь некоторое время спустя. Чтобы понять, как это происходит, рассмотрим цепь с разрывом, наподобие той, о которой говорилось в начале этой главы (фиг. 51). Подключим цепь сначала к батарее, а потом к источнику переменного напряжения. На фиг. 117 показана такая цепь, причем в разрыв включен конденсатор, т. е. две пластины, параллельные друг другу и разделенные воздушным промежутком. Под действием переменного напряжения заряды движутся то к пластинам конденсатора, то от пластин. В этом смысле говорят, что конденсатор проводит переменный ток.

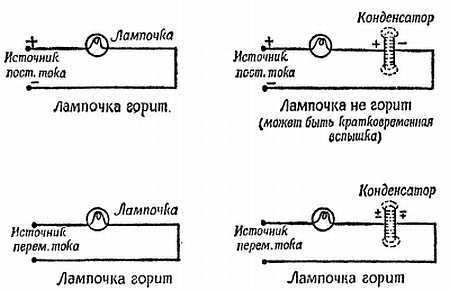
Фиг. 117. Конденсатор в электрической цепи.

_{Если конденсатор включен последовательно в цепь постоянного тока, лампочка обнаруживает в лучшем случае кратковременный импульс тока. Если цепь с конденсатором подключить к источнику переменного тока, то заряды будут то подходить к пластинам конденсатора, то уходить от них, проходя через лампочку. Поэтому лампочка горит, хотя и менее ярко, чем без конденсатора. Следуя предложению Максвелла, мы представляем себе, что через конденсатор проходит ток изменяющегося электрического поля, который создает магнитное поле с замкнутыми кольцевыми силовыми линиями.}

На фиг. 118 показано распределение зарядов на пластинах и график зависимости напряжения между пластинами от времени.

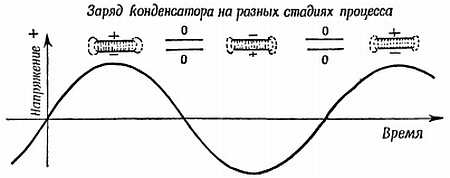
Фиг. 118. График зависимости переменного напряжения на конденсаторе от времени.

Чтобы распространить электрическое поле, существующее между пластинами, на большую область пространства, замените пластины двумя антенными стержнями, А и В.

На фиг. 119 показано электрическое поле вокруг стержней, заряженных от батареи.

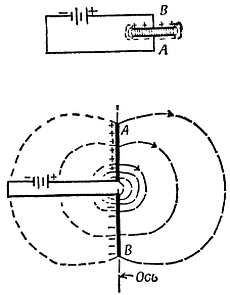
Фиг. 119. Заряжение антенной системы.

_{Пара пластин, присоединенных к батарее, заряжается (одна положительно, другая отрицательно) до тех пор, пока разность потенциалов между ними не станет равной э.д.с. батареи. Если пластины заменить стержнями, то электрическое поле вокруг заряженных стержней будет таким, как показано на фигуре. Поле симметрично, причем стержни играют роль оси симметрии. Чтобы полностью представить себе картину поля, вообразите, что приведенный рисунок вращается вокруг этой оси. Остальные компоненты схемы, провода и батарея, тоже создают электрические поля; они здесь не показаны.}

На фиг. 120, 121 представлены картины электрического поля около стержней, к которым приложено напряжение, медленно изменяющееся с течением времени по величине и направлению. Когда напряжение максимально, стержни заряжены (один положительно, другой отрицательно) так, как показано на фиг. 121, а. Фиг. 121, б соответствует моменту, когда напряжение уменьшилось вдвое; фиг. 121, в иллюстрирует состояние, в котором напряжение равно нулю. В стадиях от а до б — и от б до в заряды движутся вдоль стержней обратно к источнику, унося с собой свои силовые линии, которые постепенно исчезают. В следующую четверть периода напряжение, количество зарядов на стержнях и поле достигают максимума, но заряды на стержнях и напряжение будут противоположны этим величинам в стадиях a, б, направление поля также изменится на обратное. Затем все перечисленные величины снова изменяются до нуля, и мы возвращаемся к первой стадии процесса. Заряды нагнетаются к антенным стержням и откачиваются от них. Вдали от стержней можно обнаружить в лучшем случае слабое излучение.

Фиг. 120. Антенные стержни заряжаются от батареи (положительно и отрицательно), при этом вокруг них создается электрическое поле.

Фиг. 121. Дипольная антенна.

_{Антенна подключена к источнику переменного напряжения. Приведенные рисунки изображают картину электрического поля в окрестности обоих стержней. (Разумеется, вокруг остальной части схемы тоже существует поле.) Предполагается, что частота переменного напряжения очень мала, поэтому изменения поля происходят очень медленно. При нарастании и спадании напряжения заряды «приливают» в стержни и наоборот; при этом раскрываются и сокращаются громадные зонтики из силовых линий — возникает пульсирующее электрическое поле, которое находится в фазе с напряжением. Изображенные конфигурации силовых линий соответствуют сечению реальной картины поля в плоскости: поле на самом деле имеет пространственную картину. Чтобы представить себе ее, вообразите, что картина, изображенная в плоскости, вращается вокруг оси стержней.} 

На фиг. 122 показаны те же стадии при значительно более быстром изменении величины и направления переменного напряжения (или при значительно большей длине стержней). Удаленные части поля в каждый момент времени не получают вовремя информации об изменениях напряжения и не исчезают, подобно более близким частям. Они отделяются в виде замкнутых петель, которые потом оттесняются следующей группой силовых линий, появляющихся и увеличивающихся в размерах при новом нарастании напряжения. Представьте себе, что длинным кнутом внезапно хлопают с такой силой, что образующаяся на нем петля в результате резкого движения отрывается. От настоящего кнута петля, конечно, отделиться не может, а вот на силовых линиях поля может образоваться такая отделяющаяся петля. Вычисления, проведенные с помощью модифицированного уравнения  для движущихся зарядов, предсказывают именно такую картину. Схематические изображения картин поля, представленные на фиг. 122, 124, 125, основаны на таких вычислениях; впервые их проделал Герц, который первым же экспериментально получил радиоволны.

Фиг. 122. Дипольная антенна.

_{Антенна подключена к источнику переменного напряжения высокой частоты. Изменение напряжения происходит очень быстро.}

_{1 — источник напряжения включают в момент, когда напряжение равно нулю. Стержни не заряжены.}

_{2 — напряжение, величина заряда и поле возрастают, этим сопровождается движение зарядов по стержням (1/8 периода спустя после включения источника).}

_{3 — напряжение, величина заряда и поле возросли до максимума (1/4 периода после включения источника при незаряженных стержнях).}

_{4 — напряжение, величина заряда и поле уменьшаются, удаленные же области поля остаются на своем месте. Участки линий, ближайшие к стержням, стягиваются, и внешние области линий поля превращаются в замкнутые петли.}

_{5 — напряжение и величина заряда равны нулю (1/2 периода после включения источника). Однако поле остается в форме замкнутых петель, которые перемещаются от стержней, «отталкиваемые» вновь образующимися петлями.}

_{6 — по стержням стремительно движутся новые заряды противоположного знака, вновь создавая поле в центральной области. Это нарастающее поле «отталкивает» петли предшествующего поля в области пространства, более удаленные от стержней.}

_{7 — величина нового заряда и вновь появившееся напряжение достигают максимума. Образуется новое поле с обратным направлением стрелок» которое достигает максимума.}

_{8 — картина поля спустя 3/2 периода после показанной выше. Сюда переместились крайние петли. Новая картина поля в окрестности стержней соответствует еще одной перемене знаков.}

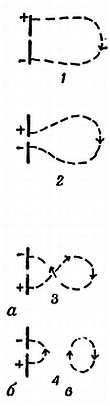
Фиг. 123. Упрощенное объяснение образования петель из силовых линий поля.

_{Проследите за исчезновением одной силовой линии.}

_{1 — при сближении зарядов, на которых начинается и оканчивается линия, происходит сближение участков линии, прилегающих к стержню, в то время как более удаленные участки остаются неподвижными.}

_{2 — можно представить себе, что заряды каждого знака переходят прямо на противоположный стержень, а не идут к источнику и обратно.}

_{3 — если бы силовая линия оставалась подобной упругой трубке, она перекрещивалась бы, как показано на фигуре а.}

_{4 — с настоящими силовыми линиями такого происходить не может, поэтому они разделяются: а —> б + в.}

Фиг. 124. Радиоволны.

_{Мгновенная картина электрического поля, излучаемого двумя короткими стержнями (такими, как на предыдущих фигурах), подсоединенными к источнику быстропеременного напряжения. Видны замкнутые петли из силовых линий поля, которые отталкиваются по мере образования у стержней новых петель и распространяются дальше в виде радиоволн. Поле в непосредственной близости к стержням, изображенное на предыдущих фигурах, здесь не показано. Радиальные стрелки указывают направление распространения мгновенной картины поля, приобретающей все большие размеры по мере удаления от антенны. Вы должны представлять себе, как эта картина поля распространяется от источника (стержней) со скоростью света, увеличиваясь в размерах по мере удаления. Группа замкнутых петель из силовых линий поля распространяется практически в радиальном направлении от источника, как только выйдет из непосредственной близости к нему. Поэтому интенсивность излучения должна следовать закону обратной пропорциональности квадрату расстояния.}

Фиг. 125. Радиоволны, испускаемые небольшой антенной, вблизи поверхности земли.

_{На фигуре показаны вертикальная антенна и поверхность земли (зеркальное изображение антенны относительно поверхности земли служит нижним «стержнем»); такая система излучает электромагнитные волны над поверхностью земли. Стрелки указывают направление распространения мгновенной картины поля, увеличивающейся в размерах по мере распространения.}

Отделившись, петли уносятся со скоростью света; находясь в движении, они и представляют собой свет, хотя их длина волны может не попадать в пределы узкой области длин волн видимого света.

Один за другим следуют периоды переменного напряжения, сопровождаемые появлением все новых и новых групп отделившихся петель-линий поля, изображенных на фиг. 124. Изменяющиеся электрические поля возбуждают в смежных областях пространства переменные магнитные поля; радиоволна — это и есть такое электромагнитное поле, распространяющееся в пространстве.

Пара стержней представляет собой простую дипольную антенну (диполь), которую используют для приема и передачи ультракоротких радиоволн. Для длинных волн требуется антенна больших размеров. Одним «стержнем» служит вся антенна, включая вертикальный провод, ведущий от нее, роль второго «стержня» играет зеркальное изображение антенны, располагающееся под поверхностью земли.

Поле и движение. На подступах к теории относительности

На первый взгляд электрическое и магнитное поля кажутся не только непохожими, но и совершенно независимыми друг от друга. Однако между ними существует связь.

1. а) Покоящиеся заряды создают постоянные электрические поля,

б) Покоящиеся магниты создают постоянные магнитные поля.

2. а) Установившийся ток в цепи создает постоянное магнитное поле (и движущееся электрическое поле, хотя оно может и не обнаруживаться).

б) Движущийся магнит создает движущееся вместе с ним магнитное поле и постоянное электрическое поле (в этом заключается принцип действия электрического генератора).

3. С изменяющимся током в цепи (например, переменным током) связаны изменяющиеся электрическое и магнитное поля. Такая цепь излучает электромагнитные волны, интенсивность излучения их становится больше, если изменения величины и направления тока происходят быстро, и цепь обладает правильно выбранной «площадью излучения».

4. Электромагнитные волны представляют собой движущееся электромагнитное поле — электрическое и магнитное поля, перпендикулярные друг к другу, которые вместе распространяются в пространстве.

Изменения поля одного вида возбуждают в соседних областях пространства переменное поле другого вида, и электромагнитная волна продолжает распространяться.

Каким образом электрическое и магнитное поля связаны между собой?

Более глубокие исследования показывают, что изменение или, образно говоря, движение поля каждого вида всегда сопровождается появлением поля другого вида: движущееся электрическое поле создает магнитное поле, а движущееся магнитное поле создает электрическое поле. Но представьте себе, что движется не поле, а сам экспериментатор. Будет ли он наблюдать такое же магнитное поле, когда он движется поперек электрического поля, создаваемого зарядом?

Если нет, значит, наш наблюдатель может сказать, что именно движется: он или заряд, а следовательно, он нашел способ обнаружить абсолютное движение. Другими словами, он может установить «верстовые столбы» в абсолютном пространстве. Только эксперимент может дать достоверный ответ на этот вопрос. Однако мы можем высказывать предположения, применяя обычную геометрию движения к законам Максвелла точно так же, как могли бы мысленно построить траекторию падающего апельсина, какой ее видит бегущий мимо наблюдатель. Размышляя таким образом, мы приходим к выводу, что законы Максвелла должны принимать какую-то иную, более громоздкую форму для любого наблюдателя, кроме «покоящегося», жестко связанного с «верстовым столбом», зафиксированным в пространстве. Но действительные эксперименты дают нам законы электродинамики в одинаково простой форме для какого угодно наблюдателя, покоящегося или движущегося по лаборатории. Что же является ошибочным: простые законы, которые подтверждает опыт, или простая геометрия, которой мы пользовались, выдвигая свое предположение?

Игнорируя это необычное противоречие, ученые XIX столетия пытались исследовать свое движение в пространстве по влиянию этого движения на опыты с электромагнитным полем. Любой измеренный эффект, пропорциональный скорости и, ясно обнаруживает наличие относительной скорости между экспериментатором и прибором, когда в лаборатории происходят изменения движений. Что же касается влияния какого бы то ни было движения лаборатории в пространстве как целого, то это влияние исключается простым вычитанием. Опыты эти показали, что неважно, как совершается относительное движение: движется ли наблюдатель, прибор или оба одновременно. Но пытались произвести и другие опыты: пытались измерить время прохождения световых вспышек по какому-либо пути и обратно в различных направлениях в пространстве. Световая вспышка представляет собой группу электромагнитных волн, распространяющихся в «пространстве», и измерение времени ее распространения могло бы дать эффект, зависящий от v². Таким образом, ученые могли бы, руководствуясь обычной геометрией, обнаружить наше движение в пространстве. Однако, несмотря на все новые и новые попытки, не удавалось обнаружить никакого эффекта. Мы уверены, что движемся, и тем не менее не обнаруживаем никакого движения. Какой же вывод мы должны сделать: что были неправильно проведены опыты, выбрана неподходящая геометрия или что неверна идея «верстовых столбов» в пространстве? Этот основной вопрос послужил толчком к созданию теории относительности.

Задачи к главе 33

Задачи 1—12 приведены в тексте главы.

Задача 13. Электрофор

Электрофор — это устройство, позволяющее получать неограниченное количество электрических зарядов. Электрофор состоит из:

а) плексигласового диска, заряжаемого трением о мех (при этом отрицательные электроны «соскабливаются» с меха и переходят на плексиглас, где остаются на поверхности или вблизи нее, поскольку плексиглас — очень хороший изолятор);

б) металлической пластины с изолирующей ручкой. Заряды получают следующим стандартным способом (после того как плексиглас потерт мехом):

1) подносят пластину на близкое расстояние к плексигласу;

2) пальцем касаются пластины, чтобы соединить ее с землей (электрическим проводником огромных размеров);

3) убирают палец;

4) удаляют пластину; на ней остается заряд, которым можно воспользоваться.

Даже если пластина касается плексигласа, с него снимается очень небольшой заряд, ибо плексиглас — очень плохой проводник.

а) Изобразите рисунками различные стадии этого процесса, проставив на них знаки «+» и «—» там, где, по-вашему, есть заряды. Проведите силовые линии поля.

б) Объясните кратко, что происходит от одной стадии до ближайшей следующей.

Задача 14. Подготовка к опыту Милликена, посвященному измерению заряда электрона

Очень маленькой капельке жидкости (вылетающей из пульверизатора) сообщают заряд, равный заряду одного электрона. Капельку впускают в пространство между двумя горизонтальными металлическими пластинами, расположенными одна над другой. Пластины подсоединяют к батарее, которая создает в промежутке между ними вертикальное электрическое поле напряженностью 100 000 ньютон/кулон. (Это значение напряженности можно вычислить, зная напряжение батареи и расстояние между пластинами.) Если величина поля как раз достаточна, чтобы заставить капельку парить в воздухе, не поднимаясь и не опускаясь, то какова масса капельки?

Дано: ЗАРЯД ЭЛЕКТРОНА = -1,6∙10^-19 кулон.

(Этот расчет, проведенный в обратном направлении, соответствует методу, посредством которого Милликен измерил заряд электрона.) Сравните полученный результат с пределом измерения наиболее чувствительных химических микровесов, близким к одной миллиардной грамма, или 10^-12 кг.

Задача 15. Предварительная задача, связанная с опытом Милликена

При падении крошечной дождевой капельки сила сопротивления воздуха, действующая на капельку, изменяется прямо пропорционально скорости. (Это тщательно проверено опытом.) Силы сопротивления, действующие на капли разных размеров, прямо пропорциональны радиусам капель. Следовательно, сила сопротивления воздуха = К∙r∙v, где К — постоянное число, известное из опытов по изучению движения воздуха в трубах. (Предположим, значение К таково, что произведение К∙r∙v дает силу в ньютонах.) Когда дождевая капля начинает падать, она сначала движется ускоренно, но вскоре достигает постоянной скорости.

а) Какие две силы действуют на каплю в любой стадии ее падения?

б) Чему должна быть равна результирующая сила, когда капля падает с постоянной скоростью?

в) Напишите уравнение, вытекающее из а) и б), используя К и другие коэффициенты, приведенные выше.

г) Предположим, что другая капля имеет вдвое больший радиус. Какова ее масса? Покажите из вашего уравнения в), что эта капля будет падать в четыре раза быстрее.

Задача 16. Электрические поля и закон обратной пропорциональности квадрату расстояния: подготовка к опыту Милликена

Мы используем электрические поля в целом ряде измерений в «атомной физике». Приводимая ниже задача поможет вам понять, что такое электрические поля.

НАПРЯЖЕННОСТЬ ГРАВИТАЦИОННОГО ПОЛЯ определяется как СИЛА (в ньютонах), действующая на ЕДИНИЦУ МАССЫ (1 кг). Она измеряется в ньютон/кг.

НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ определяется как СИЛА (в ньютонах), действующая на ЕДИНИЦУ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА (1 кулон). Она измеряется в ньютон/кулон.

а) Какова (примерно) напряженность гравитационного поля Земли, т. е. с какой силой (в ньютонах) Земля притягивает 1 кг

— в вашей лаборатории?

— в любой точке на расстоянии 6340 км от центра Земли?

— в любой точке на расстоянии 12 680 км от центра Земли?

б) Напряженность гравитационного поля Земли можно вычислить другим методом, исходя из гравитационной постоянной G. Это более утомительный и нерациональный способ, если мы уже знаем напряженность непосредственно из наблюдений за падающими телами, но он иллюстрирует метод, используемый для определения напряженности электрических полей. Покажите, что можно получить то же самое значение напряженности поля в лаборатории, воспользовавшись следующими данными:

Гравитационная постоянная G = 6,67∙10^-11 (ньютон∙м²/кг²), входящая в формулу F = G∙M₁∙M₂/d².

Расстояние от лаборатории до центра Земли ~= 6,34∙10⁶ м.

Масса Земли ~= 6,0∙10²¹ т ~= 6,0∙10²⁴ кг.

Используя формулу закона всемирного тяготения, вычислите приближенно силу, с которой Земля притягивает пробную массу 1 кг вблизи поверхности Земли. Это и есть напряженность гравитационного поля Земли в данной точке.

в) Воздушному шарику, диаметр которого 0,2 м (радиус 0,1 м), сообщают заряд 1 микрокулон, т. е. 1∙10^-6 кулон. (Это большой заряд для такого шарика.) Вычислите напряженность электрического поля на расстоянии 0,5 м от центра шарика. Постоянная , входящая в формулу закона обратной пропорциональности квадрату расстояния для силы взаимодействия зарядов, равна 9∙10⁹ (ньютон∙м²/кулон). (Постоянная  появляется вместо G.)

г) Вычислите напряженность электрического поля на расстоянии 1,0 м от центра шарика.

д) Когда мы имеем дело с электрическим полем в пространстве между двумя параллельными пластинами (таким полем пользовался Милликен при измерении заряда электрона, оно используется в электронно-лучевых трубках для отклонения пучка электронов)г мы исходим из опытных данных о том, что это поле однородно. Это значит, что поле имеет одинаковую напряженность всюду в пространстве между пластинами и направлено прямо от одной пластины к другой перпендикулярно пластинам. Если мы знаем напряжение между пластинами (допустим, что к пластинам подключен вольтметр параллельно батарее, подсоединенной к пластинам для создания поля), то мы можем вычислить поле, как в следующем примере. Предположим, что разность потенциалов между двумя параллельными пластинами, отстоящими друг от друга на 0,4 м, равна 15 000 в.

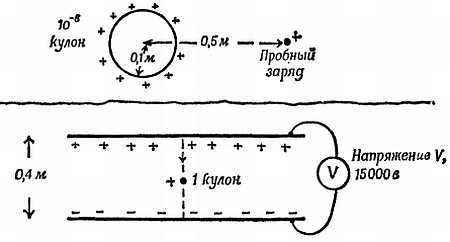
Фиг. 126. К задаче 16.

1) Разность потенциалов 15 000 в между пластинами означает, что…

Дополните эту фразу.

2) Исходя из 1), вычислите энергию, сообщаемую электрическим полем 1 кулону, проходящему от одной пластины до другой, в джоулях.

3) Предположим, что 1 кулон, помещенный в поле в качестве пробного заряда, испытывает силу X ньютонов (т. е. предположим, что напряженность поля между пластинами равна X ньютон/кулон). Представим себе, что эта сила движет кулон от одной пластины до другой. Какое количество энергии будет таким образом сообщено кулону? (Обратите внимание, что оно в точности равно произведению СИЛА∙ПУТЬ.)

4) Напишите уравнение, из которого следует, что в 2) и 3) в ответе получается одна и та же величина. Решите это уравнение и найдите напряженность поля X.

Задача 17. Задачи с применением математического анализа. (Эти задачи имеют важное значение для изучения атомной физики.)

Чтобы детально разработать любую картину строения атома, вроде простой модели Бора, необходимо знать потенциальную энергию отрицательного электрона на расстоянии r от положительного ядра. (Точно так же, попытавшись рассчитать орбиту планеты, мы столкнемся с необходимостью определить потенциальную энергию тела в гравитационном поле.) Для этого нам нужно знать разность потенциалов V между бесконечностью и точкой, удаленной от заряда ядра Q на расстояние r. Если заряд +1 кулон при перенесении его из бесконечности в точку, удаленную от ядра на r, приобретает электрическую потенциальную энергию V дж, то электрон с зарядом е приобретает энергию V∙e дж. Поскольку е отрицательно и равно —1,6∙10^-19 кулон, электрон при переводе его из бесконечности на орбиту с радиусом r теряет потенциальную энергию. Вот почему электрон не может покинуть орбиту, пока ему не будет сообщена добавочная энергия путем бомбардировки. Итак, вы найдете выражение для V, которым пользуются в атомной физике. Оно получается в результате вычисления работы, совершаемой против силы отталкивания ∙Q(1)/d² при перенесении +1 кулон из d = бесконечности в d = r. Сила отталкивания меняется с изменением расстояния d, поэтому определить V простым перемножением СИЛА∙ПУТЬ нельзя. Вместо этого мы должны разбить весь путь на очень короткие участки, вычислить работу на каждом участке и сложить результаты. Разбивая путь на все более короткие участки, мы получим в пределе то, что дает метод математического анализа, называемый интегрированием, (Существуют приемы, позволяющие проделать этот расчет без помощи математического анализа, однако каждый, кто в состоянии проследить за подобными выкладками, смог бы за это время познакомиться с математическим анализом, доставив себе большое удовольствие.) Приведем вывод формулы математического анализа, заменив букву d на х.

Предположим, что пробный заряд +1 кулон проделал часть пути, находясь на расстоянии х, и мы перемещаем его еще на некоторый отрезок пути — dx. (Символ d употребляется вместо Δ в случае предельного перехода и обозначает бесконечно малую величину, а знак минус указывает на перемещение в направлении начала отсчета величины х, т. е. означает отрицательное приращение х.) Тогда работа на этом отрезке пути равна

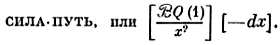
Следовательно,

V = ПОЛНАЯ РАБОТА = СУММА ВСЕХ ЭЛЕМЕНТАРНЫХ РАБОТ НА ПУТИ ИЗ БЕСКОНЕЧНОСТИ ДО х = r

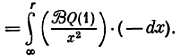
Работа, совершаемая внешней силой, переходит в потенциальную энергию заряда в электрическом поле. Записанный интеграл равен потенциальной энергии, приходящейся на единицу заряда.

а) Произведите интегрирование, помня, что  — постоянная, равная 9,0∙10⁹, a Q — заряд центрального ядра — тоже постоянная величина.

б) Решение задачи а) дает величину V на расстоянии r от точечного заряда Q. Оно дает, кроме того, величину V на поверхности заряженного шара радиуса r, несущего заряд Q. Почему?

в) Исходя из б), оцените потенциал металлического шара величиной с бейсбольный мяч (r ~= 0,05 м), несущего заряд 1 микрокулон (10^-6 кулон). Потенциал шара выражается в вольтах.

г) В соответствии с простыми моделями атома «радиус» атома водорода — то расстояние от ядра, на котором электрон проводит большую часть времени, — близок к 0,5 А° (= 0,5∙10^-10 м). Заряд электрона, равен —1,6∙10^-19 кулон; ядро, находящееся в центре, обладает таким же по абсолютной величине положительным зарядом.

1) Вычислите величину V, обусловленную зарядом ядра, равным +1,6∙20^-19 кулон, на «наружной поверхности» атома (для атома водорода).

2) Вычислите потенциальную энергию электрона в джоулях там же, умножив V на заряд электрона, равный —1,6∙20^-19 кулон.

Затем разделите полученную величину на заряд электрона, чтобы выразить потенциальную энергию в электронвольтах. (Обратите внимание на то, что эта потенциальная энергия отрицательна. В модели Бора электрон обладает, кроме того, кинетической энергией, которая численно ровно вдвое меньше потенциальной и, конечно, положительна. Таким образом, половина найденного здесь вами значения указывает энергию, которую необходимо затратить, чтобы выбить электрон из атома и превратить атом в ион. Опыты по бомбардировке атомов водорода показывают, что для атома водорода эта энергия равна 13,6 электронвольт.)

3) α-частицами, несущими заряд +2е, обстреливают атомы золота. Изредка какая-нибудь α-частица отлетает строго назад. В этом случае мы представляем себе, что α-частица движется к атому золота, преодолевая силу отталкивания со стороны большого положительного заряда ядра атома, пока не потеряет всю свою кинетическую энергию, которая переходит в потенциальную энергию частицы в электростатическом поле. После этого α-частица летит назад. Ив приведенных ниже данных (все они взяты из опытов) оцените, на какое самое близкое расстояние α-частица приближается к ядру атома золота. Сравните свой ответ с традиционным «размером» атома (радиус порядка 0,5∙10^-10 м).

ОПЫТНЫЕ ДАННЫЕ, α-частица, вылетающая из ядра атома радия, имеет:

— скорость v ~= 1,6∙10⁷ м/сек,

— массу m ~= 6,6∙10-²⁷ кг,

— заряд 2e = + 2∙1,6∙10^-19 кулон.

Ядро атома золота значительно более массивное, а заряд его равен 79е = 79∙1,6∙10^-19 кулон.