Глава 44. Дальнейшая теория и эксперимент. Физика сегодня

«Каждая новая теория… полагает, что она наконец является той счастливой теорией, которая дает «правильный» ответ… Если мы будем знать, что логика, математика, физическая теория являются лишь нашими изобретениями для формулировки в компактной и доступной для обращения форме того, что мы уже знаем, и, подобно всем изобретениям, не достигают полного успеха в том, для чего они были предназначены, и еще меньшего успеха вне области своего первоначального предназначения, и что наша единственная надежда проникнуть с помощью этих изобретений в нечто совсем неизвестное основана на прошлом опыте, почему же иногда мы были настолько удачливы, что смогли продвинуться хоть на короткое расстояние за счет приобретенной инерции?»

П. У. Бриджмен, 1936 «Природа физической теории»

«В полночном молчании времени снов,

Когда вы освобождаете свое воображение…»

Роберт Браунинг

[Эта последняя глава не столько заканчивает курс, сколько связывает его с будущими самостоятельными исследованиями и чтением литературы. Ее следует читать на досуге, для «души». Она не может полностью снабдить вас всеми современными знаниями в окончательном виде. Вместо этого у вас останутся сомнения и обрывки незаконченного знания — а этим характеризуются границы любой развивающейся науки.]

КЛАССИЧЕСКАЯ ФИЗИКА

К началу этого века на протяжении жизни примерно сотни (или около этого) поколений человечество создало огромный каркас физической науки:

∙ Статика блоков и тросов, колонн, мостов… правила равновесия

∙ Динамика движущихся тел, сила и масса, законы движения, энергия и импульс

∙ Гидростатика насосов, давление воздуха, условия плавучести судов и их остойчивости…, законы давления в жидкости, закон Бойля…

∙ Гидродинамика потоков жидкости как при ламинарном, так и при вихревом движении

ОБЪЕДИНЕНЫ ЗАКОНАМИ НЬЮТОНА

∙ Электромагнетизм зарядов, токов, магнитов…, полей…

∙ Оптика световых лучей, движущихся по прямой и отклоняющихся под действием линз с образованием изображения, волновое поведение при дифракции и интерференции, электромагнитная теория света

ОБЪЕДИНЕНЫ ЗАКОНАМИ (УРАВНЕНИЯМИ) МАКСВЕЛЛА

∙ Акустика: физика музыкальных инструментов и звуковые волны

∙ Теплота: термометрия и калориметрия, теплота как форма энергии

∙ Свойства вещества: упругость, трение твердых тел и жидкостей, поверхностное натяжение и т. д

ОБЪЕДИНЕНЫ С МЕХАНИКОЙ

∙ Кинетическая теория газов и рассмотрение теплоты как молекулярного движения (движения молекул)

∙ Поведение атомов и молекул в кристаллических структурах, при поверхностном натяжении, упругость, диффузия

МЕХАНИКА, ПРИМЕНЕННАЯ К СОВОКУПНОСТИ НЕВИДИМЫХ МАЛЫХ ЧАСТИЦ

∙ Термодинамика: соотношение между теплотой, работой и материей

РАССМАТРИВАЛИСЬ КАК ВСЕОБЩИЕ ПРАВИЛА

Рядом с физикой в огромную науку о структуре и свойствах молекул развилась химия:

Неорганическая Химия: химические реакции и их характеристики, интерпретируемые в терминах элементов, соединений, атомов и молекул

Органическая Химия: изучение углеродных соединений, содержащихся в живой материи: почти бесконечное семейство молекул — исследованных, внесенных в каталоги, наглядно изображенных «структурными формулами» и даже синтезированных из элементов, — заключенное в пределах от простой молекулы СО₂ до огромных и сложных протеиновых молекул.

Физическая Химия: изучение физического действия химических процессов: теплота реакции, теплота растворения; измерение массы молекулы по давлению паров, по изменению осмотического давления, по изменению точки замерзания растворов; механика и статистика химических реакций и т. п.

Однако между Физикой и Химией оставался большой разрыв. Химики все шире использовали физические инструменты, но, как ни странно, физики зачастую оставались в стороне и теряли хорошие возможности связать химические превращения и достижения в области физических знаний.

Выделились, сохраняя в то же время сильную связь с физикой и химией, другие науки — астрономия, минералогия и т. п. Во всей физической науке возникли в качестве надежных результатов и критериев определенные всеобщие правила, или Принципы: векторное сложение скоростей, сил и т. п.; галилеевская относительность; ньютоновские законы движения; постоянство массы; сохранение импульса, сохранение энергии; закон тяготения; закон Кулона и содержащие его уравнения Максвелла; трактовка света и др. как электромагнитных волн; неделимость атомов, идентичность всех атомов данного элемента.

Физику, развитую в это время, называют теперь Классической Физикой. Она казалась хорошо понятой, завершенной (за исключением мелких деталей), точной и вполне удовлетворительной. Кое-что из нее было распространено вниз (по масштабной шкале изучаемых объектов) на атомы и молекулы и вверх на солнечную систему в предположении, что там применимы те же самые общие правила и принципы. Физику падающего камня, отскакивающего мяча и т. п. самонадеянно экстраполировали[175] на планеты и молекулы газа.

НОВАЯ ФИЗИКА

Уверенность и полнота классической физики были опрокинуты в этом реке пятью великими достижениями:

1. С открытием электронов и радиоактивности была обнаружена атомная структура. Атомы можно разрушить, и они даже могут превращаться в другие атомы. Возникла ядерная модель атома.

2. Теория относительности разъяснила некоторые парадоксы и изменила наши представления о пространстве, времени, массе и полях.

3. Было обнаружено, что у света (и всех других видов излучений) энергия упакована в «снаряды», хотя распространяется он подобно волнам. Возникла квантовая теория. Это привело к модели атома Бора, который руководствовался своим принципом соответствия.

4. Было обнаружено, что объекты атомной физики (электроны, ядра…) ведут себя и как волны, и как частицы. Двойственное поведение «волна-частица», таким образом, оказалось свойственным и излучению, и частицам вещества. Это привело к новой теории, «квантовой механике», с важными философскими идеями принципа неопределенности и дополнительности.

5. Было открыто множество новых субатомных частиц: электроны, ядра, нейтроны, мезоны, нейтрино и недавно много других.

Из этих достижений указанное в пункте 1 было описано в предыдущей главе, указанное в пункте 2 — в гл. 31. Достижения, указанные в пунктах 3 и 4, обсуждаются в этой главе. Мы не будем касаться описания новейших частиц, указанных в пункте 5,— экспериментальное и теоретическое наступление на них продолжается, и нам остается с нетерпением ожидать решения существующих сегодня загадок ядерных сил и структуры ядер.

Атомная физика 1890–1915 гг.

В начале этого века «атомная физика» была юной наукой, быстро растущей на базе новых экспериментов с электричеством. Старая наука об электричестве и магнетизме была построена в прошлом веке, обеспечив последовательные знания о зарядах, токах и полях. С практической стороны ученые и инженеры развили — посредством интерполяции — промышленное использование этой науки, создав электромоторы, измерительные приборы, лампы, силовые системы и линии связи. С теоретической стороны экспериментальные законы, объединенные в уравнениях Максвелла, логически привели к предсказанию радиоволн.

На грани веков радиоволны были получены с помощью электричества, хотя еще и не использовались, и было установлено, что свет представляет собой очень короткие радиоволны. Затем, когда картина казалась близкой к завершению, появились новые сведения об атомах и электронах сразу из нескольких различных источников: открытие рентгеновских лучей, радиоактивности, фотоэлектрического эффекта и эмиссии электронов из нагретых металлов; исследования ионов и электронов в разрядных трубках. Оказалось возможным расчленить атомы на положительные ионы и универсальные электроны с доступными измерению свойствами. В начале века была предложена и проверена картина внутренней структуры атомов.

В первой четверти этого века количество знаний об атомах увеличилось, но появились некоторые серьезные парадоксы. Резерфорд предложил хорошую теоретическую модель атома: малое по размерам массивное ядро окружено движущимися электронами подобно крошечной солнечной системе. Электроны все одинаковы, с массой, равной 1/1840 массы атома водорода, и с универсальным зарядом е = —1,6∙10^-19 к. Ядро невероятно мало; его диаметр составляет 1/10 000 А° — атомной единицы длины. Ядра являются носителями положительного заряда, варьирующегося от +е для ядра водорода (протона) до +92 е для ядра урана. Из заряда исходит электрическое поле, убывающее обратно пропорционально квадрату расстояния от заряда. Число Z единиц +e, содержащихся в заряде, дает «атомный номер» элемента и определяет его место в периодической системе химических элементов. Последнее объясняется тем, что Z дает также число электронов, окружающих ядро в нейтральном атоме. Эти электроны, сгруппированные по некоторой схеме в слои, или оболочки, отвечают за химические свойства. Атомы, которые теряют или приобретают электроны, становятся ионами — активными агентами во многих химических процессах. Электрические силы между положительно и отрицательно заряженными ионами связывают некоторые молекулы, например молекулу соли Na⁺—Сl^-. В других химических соединениях, наоборот, электроны находятся в совместном владении атомов, вместо того чтобы быть переданными полностью какому-либо атому. Все атомы и молекулы удерживаются электрическими силами. У легчайших атомов (водород, гелий, литий…) их немногочисленные электроны находятся далеко от ядра, в огромной области пространства[176], где действует поле, подчиняющееся закону обратных квадратов. Наиболее тяжелые атомы (золото, уран и т. д.), с числом электронов, близким к сотне, удерживают эти электроны в нескольких слоях. Самые внутренние группы (остающиеся все еще далеко от ядра) сильно связаны электрическим полем большого заряда ядра, и обычные химические действия на них не влияют. Однако их можно разрушить при бомбардировке электронами большой энергии, фотонами рентгеновских лучей и т. п.

Фиг. 171. Атомные картины.

_{а — атом Резерфорда; б — модели атома Бора; в — ионы в кристалле соли.} 

Только самые внешние группы электронов участвуют в химических превращениях. Для этих электронов притяжение к ядру в значительной степени нейтрализовано отталкиванием от более внутренних электронов, оказывающих «экранирующее» действие. Поэтому самые внешние электроны слабо связаны и легко обмениваются или обобществляются, создавая силы, объединяющие атомы в химических соединениях, и поля, которые запасают «химическую энергию». Данные химии наводят на мысль о том, что только несколько электронов принадлежит к этой наиболее внешней группе, и более поздняя теория Бора в деталях подтвердила картину: один электрон в водороде, натрии, калии и других металлах, которые, теряя его, образуют положительно заряженные ионы («+» ионы); 2 в меди и других металлах, которые образуют «++» ионы; 3 — в алюминии… В хлоре самая внешняя группа содержит 7 электронов и может захватить еще один, чтобы образовать компактную стабильную группу из восьми электронов и превратить атом в ион Сl^-, электронная структура которого подобна структуре нейтрального атома аргона. (Именно поэтому натрий так легко соединяется с хлором, образуя соль, в которой атомы остаются ионизованными даже в твердом кристалле.) Кроме этих предположений, следующих из данных химии, ясной схемы пространственного распределения электронов не было. И фордовская модель оставляла нерешенным неприятный парадокс: вращающиеся по окружности электроны должны были бы излучать электромагнитные волны[177] и двигаться по свертывающейся спирали все быстрее и быстрее — инфракрасный свет, затем красный, зеленый…, ультрафиолет…, рентгеновские лучи…, — что привело бы к быстрому разрушению атома. Ясно, что на самом деле атомы не разрушаются подобным образом. Мы не видим таких «сгорающих» атомов, а, напротив, обнаруживаем, что они стабильны. Почему?

Кое-что было известно о структуре самих ядер. Радиоактивные элементы испускают α-, β- и улучи с такой энергией, которая свидетельствует об их ядерном происхождении. Масс-спектрографы показали, что ядерные массы представляются почти целыми числами, умноженными на массу протона. Поэтому теории ядерной структуры исходили из представления о компактной группе протонов и электронов, удерживаемых вместе специальными силами. Теперь мы видим, что модель была неудобной: электроны настолько легки, что их длина волны слишком велика для того, чтобы поместиться внутри измеренных предельных размеров ядра. Кроме того, существовала проблема сохранения спина. С открытием нейтрона были предложены более подходящие компоненты ядер. Теперь стали считать, что они состоят из протонов и нейтронов[178], каким-то образом очень сильно связанных.

При распаде радиоактивного атома выделяется огромное количество энергии, которое можно точно измерить. Но для данного одиночного радиоактивного атома нельзя предсказать точно время, которое он проживет до распада. Мы можем указать только вероятностную величину, такую, как период полураспада для большого количества атомов. Понаблюдайте за счетчиком Гейгера, регистрирующим альфа-частицу, — вы увидите, что альфа- частицы появляются в произвольные моменты времени совершенно случайно, подобно каплям дождя на жестяной крыше. К началу 1900-х годов физики уже обращались к статистической точке зрения по другим поводам. Она была хорошо проверена в кинетической теории, где было видно, что регулярные характеристики и свойства, такие, как постоянное давление газа, устойчивый поток газа…, закон Бойля…, являются статистическими средними, характеризующими огромное скопление молекул. Теперь оказалось, что вероятность определяет распад радиоактивных ядер, бегство альфа-частиц из ядерной толчеи. Каким образом большинство ядер постоянно остается в виде целого, в то время как другие взрываются совершенно случайно? Этот вопрос адресован новой точке зрения, новой теории.

Относительность, 1905 г.

Тем временем была развита и принята на вооружение теория относительности. С философской стороны она проповедовалась как реформирующее учение: нельзя наделять картину природы деталями, которые нельзя проверить. Нельзя даже задавать вопросы, которые предполагают существование таких деталей. (Например, нельзя наделять электроны ненаблюдаемыми свойствами, спрашивая, какого они цвета, или изображая для них отчетливые орбиты.) С собственно физической стороны теория относительности предсказала различные эффекты и явления, наблюдаемые в опытах с движущимися объектами. Вот некоторые из них:

I. Покоящийся (или движущийся мимо объекта) наблюдатель обнаружит у движущегося объекта увеличенную массу m, большую, чем его «масса покоя» m₀. Эта масса m будет расти с увеличением скорости, стремясь к бесконечности при приближении скорости объекта к скорости света. Следовательно, никакие материальные объекты нельзя ускорить настолько, чтобы они двигались быстрее света, поскольку для этого потребовалась бы бесконечная сила.

II. С любого вида энергией связана масса, величина которой равна энергии, деленной на квадрат скорости света: m = Е/с².

III. Следует считать, что любое тело массы m обладает полной энергией mс². (Эта величина включает кинетическую энергию тела и его «энергию покоя» m₀с², связанную с его внутренней структурой.)

IV. Прошедшее, настоящее и будущее не всегда абсолютно разделены. Движущиеся по-разному наблюдатели будут делать разные заключения о некоторых событиях (далеко разделенных в пространстве или очень близких во времени). Один наблюдатель может обнаружить, что события Р и Q произошли одновременно, другой наблюдатель, движущийся с иной скоростью, может увидеть, что Q произошло раньше Р, а третий наблюдатель знает, что Р произошло раньше Q. Таким образом, теория относительности предостерегает нас от самоуверенного обращения с причиной и следствием[179].

V. Все наблюдатели, как бы они ни двигались, при измерении получат одну и ту же величину скорости света — движение к источнику или от него никак не повлияет на результат измерения. Это было исходным предположением, из которого были выведены правила теории относительности. Теперь мы обобщим его в более широкое требование ко всем измерениям, а именно: ВСЕ ЗАКОНЫ ФИЗИКИ ИМЕЮТ ОДИНАКОВУЮ ФОРМУ ДЛЯ ВСЕХ НАБЛЮДАТЕЛЕЙ, НЕЗАВИСИМО ОТ ИХ ДВИЖЕНИЯ ОТНОСИТЕЛЬНО ПРОИСХОДЯЩЕГО В ПРИРОДЕ СОБЫТИЯ[180].

Модели

В начале этого века стало выясняться, что при построении «моделей» природы, будь то крошечные атомы или огромные звездные галактики, были сделаны очень далеко идущие предположения. Зная правила, выведенные из экспериментов, масштаб которых сравним с размерами человека[181], мы рискнули предположить, что они справедливы для атомов. Мы применили макроскопическую физику к микроскопической природе. Мы интерпретировали микроскопическую природу на языке макроскопических механизмов — ускоряющихся платформ, летающих бейсбольных мячей и т. п. До тех пор, пока модель была плодотворной — давала понятную интерпретацию результатов предложенных экспериментов и подтверждалась результатами различных опытов, — она была хорошей. Но после предупреждения теории относительности, прозвонившего ученым прямо в уши, они стали гораздо более осторожными в высказываниях о справедливости своих моделей. Их студенты были склонны считать, что модель объясняет причину, но наиболее мыслящие из них не раз останавливались при попытке объяснить почему («мы знаем из нашей модели, что это происходит потому, что…»), предпочитая говорить, что («в рамках нашей модели это выглядит подобно… и, возможно, мы увидели бы в эксперименте, будет ли…»). Это старый урок, никогда полностью не выученный — если бы это случилось, ученые впали бы из легковерного восхваления в сверхосторожное отрицание, — но уроку предстоит повторяться снова и снова. Как хорошему ученому вам следует быть подозрительным в отношении моделей. Но вы не должны рассматривать модели как нечто детское. Они играют важную роль в методах, которыми пользуется человеческий ум для познания и обучения. Когда наши чувства сообщают нам что-либо совершенно новое, мы прежде всего мысленно стремимся найти что-нибудь известное, что напоминает нам это новое. Мы очень прочно прикрепляем к новым вещам старые известные ярлыки и очень медленно склоняемся к новым взглядам[182]. Даже те способные современные ученые, которые наиболее громко призывают к операционалистским методам — «описывать все в терминах методов наблюдения», — оставляют свое воображение свободным для моделей, когда они размышляют о новых разработках.

РАЗВИТИЕ КВАНТОВЫХ ИДЕЙ, 1900–1915 гг.

Традиционные модели в нескольких областях физики были опровергнуты открытиями, указывающими на странные свойства света и других видов излучений: «порции» энергии. Когда уже казалось установленным, что свет представляет собой электромагнитные волны, в экспериментах стали обнаруживать, что он также состоит из определенных малых порций энергии, подобных частицам. Это квантовое[183] представление возникло из нескольких парадоксальных противоречий между экспериментами и классической теорией[184].

Оно разрешает конфликты одним правилом, модифицирующим классическую физику: Любой обмен энергией между веществом и излучением происходит лишь определенными порциями энергии, «квантами». Для каждой порции или кванта

ЭНЕРГИЯ = (УНИВЕРСАЛЬНАЯ ПОСТОЯННАЯ, h)∙(ЧАСТОТА ИЗЛУЧЕНИЯ).

Таким образом, дискретны не только вещество и заряды, поделенные на части в виде атомов и электронных зарядов, но в определенных важных обстоятельствах дискретна также и энергия. Наименьшей величины (атомной единицы) энергии не существует, но (для определенных форм энергии) у величины отношения энергии к частоте имеется универсальный «атом», или единица, h. Это квантовое ограничение выглядит безобидным — особенно для читателей, слышавших об этом раньше, — но оно вступает в противоречие с ньютоновской механикой, если ее применять к молекулам, атомам, электронам…:

1) Раскалите добела кусок черного металла так, чтобы он испускал интенсивный поток излучения: ультрафиолет + видимый свет + инфракрасное излучение + радиоволны. Общие соображения, основанные на ньютоновской механике, предсказывают, что больше всего энергии будет излучаться в области ультрафиолета (самая короткая длина волны, наибольшая частота). Но на самом деле это неверно. Термоэлемент, измеряющий интенсивность излучения, показывает, что максимум потока энергии приходится на середину спектра. Это противоречие было известно в 1900 г. и впервые привело к предположению о существовании квантового ограничения. При наложении этого ограничения механическая теория предсказывает наблюдаемый спектр.

2) Нагревайте твердый образец или газ и измеряйте удельную теплоемкость при различных температурах. Ньютоновская физика предсказывает, что при неизменных прочих условиях удельная теплоемкость остается постоянной, не зависит от температуры. Неверно. Измеренная величина удельной теплоемкости при изменении температуры от очень низкой до очень высокой растет от очень малой величины до величины, предсказываемой классической физикой. Квантовое ограничение предсказывает это (см. гл. 30).

3) Попадая на поверхность металла, свет может вырвать оттуда электроны. По классической механике мы представили бы, что приходящие на поверхность световые волны все сильней и сильней раскачивают электрон, «привязанный» к атому металла, до тех пор пока электрон не оторвется на свободу. С этой точки зрения, чтобы достаточно сильно раскачать электрон слабым светом, всегда необходима длительная выдержка; кроме того, очень сильный свет (большой интенсивности) может выбрасывать электроны с большей энергией. Неверно. Независимо от того, тусклый свет или яркий, электроны вылетают с одной и той же полной энергией. Этот «фотоэлектрический эффект» оказался легко поддающимся объяснению и расчету после того, как Эйнштейн предположил, что энергия света упакована в «снаряды», порции.

4) Определенные экспериментальные свойства спектров кажутся странными с точки зрения классической физики. В последнем столетии были измерены и выражены простыми формулами интервалы между яркими линиями в спектре горящих газов. Классически их нельзя «объяснить». Аналогичные закономерности проявляются в крайней коротковолновой части спектров рентгеновских лучей. Бор показал, каким образом квантовая теория может дать хорошее объяснение этим фактам и обеспечить широкую область для дальнейшей интерпретации.

В следующих разделах — более детально обсуждаются все эти вопросы, при решении которых были сформированы основы квантовой теории.

Спектр белого света

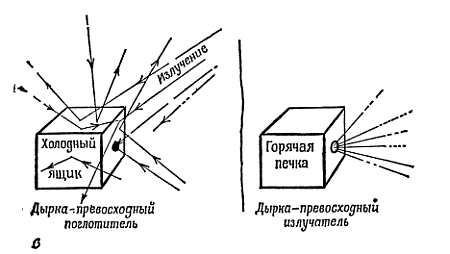
Раскалите добела кусок черного металла и проанализируйте его излучение. Еще лучше, разогрейте печку и позвольте излучению выходить через дырку в ее стенке. Вспомните, что хороший поглотитель должен быть и хорошим излучателем [гл. 26, задача 23, и гл. 4, опыты 6, ж) и з)]. Самый лучший излучатель — это абсолютно черное тело. Дырка в ящике является хорошим поглотителем: все, что попадает внутрь, будет отражаться там от стенки к стенке до тех пор, пока совсем не поглотится, — никакая черная краска на собачьей конуре не выглядит чернее открытой для собаки дверцы. Поэтому дырка должна быть абсолютным излучателем. Внутри печки излучение должно содержать полный набор волн, типичный для излучения «черного тела», а весь комплект содержащегося внутри набора выходит через дырку. Разложите излучение в спектр с помощью дифракционной решетки и измерьте с помощью зачерненного термоэлемента поток энергии в различных областях. График на фиг. 173 показывает результаты такого эксперимента.

Вспомните, что решетка разделяет свет на составляющие по длинам волн, и это разделение показывает, что у красного света длина волны примерно вдвое больше, чем у голубого.

Простую гармоническую волну характеризуют три величины:

I) длина волны, λ — расстояние от одного гребня до другого;

II) частота f — число полных длин волн, прошедших мимо наблюдателя в секунду, или число колебаний источника в секунду, или число колебаний любого датчика (в секунду), на который, проходя мимо него, действует волна;

III) скорость v, с которой перемещается профиль волны.

За 1 сек профиль волны смещается на расстояние v, а мимо исходной точки проходит f таких профилей длиной λ. Следовательно, v = f∙λ.

СКОРОСТЬ = ЧАСТОТА ∙ (ДЛИНА ВОЛНЫ)

для любой периодической волны.

Для света в воздухе или вакууме и— универсальная величина 3∙10⁸ м/сек, которую мы обозначаем буквой с. Обозначим еще частоту через v вместо f (v — буква греческого алфавита, аналогичная русской «н», читается «ню»). Тогда c = v∙λ, и частота v = c/λ. Поскольку с — постоянная, частота обратно пропорциональна длине волны. Чем меньше длина волны, тем больше частота. Приведенная ниже таблица грубо показывает некоторые значения этих величин.

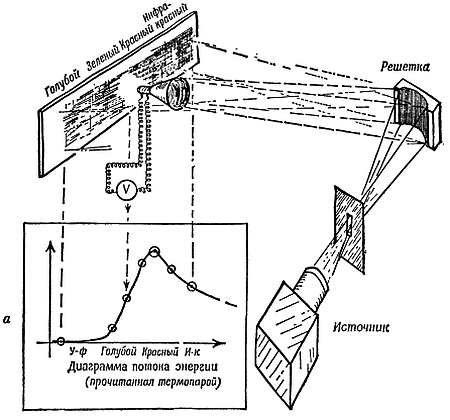
Фиг. 173. Энергетический спектр излучения.

_{а — экспериментальное устройство; б — детали термопары; в — дырка — превосходный излучатель типа «черного тела».}

Обратимся к теории и посмотрим, что она предсказывает для такого графика, если исходить из знания других отраслей физики.

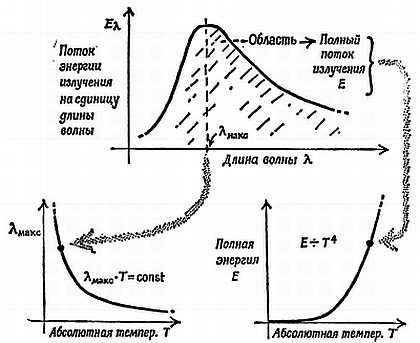
Надежные термодинамические аргументы приводят к некоторым вполне определенным предсказаниям о полном излучении «черного тела» при различных температурах:

1. Закон Стефана:

(ПОЛНЫЙ ПОТОК ЭНЕРГИИ во всем спектре) ~ (АБСОЛЮТНАЯ ТЕМПЕРАТУРА ИЗЛУЧАТЕЛЯ)⁴

или

E ~ T⁴ 

2. Закон Вина:

Длина волны λ_макс, на которую приходится максимум графика, показывающего зависимость энергии излучения от длины волны, обратно пропорциональна абсолютной температуре, так что

λ_макс∙T = Const.

Эксперименты подтверждают справедливость этих законов вплоть до наибольших энергий, которые можно измерить газовым термозвезд по шкале Кельвина. Оба закона дают одинаковую температуру поверхности Солнца примерно 6000° К.

Фиг. 174. Излучение (экспериментальные факты).

Но дальнейшее рассмотрение на основе традиционной[185] (ньютоновской) механики предсказывает также детальную форму графика, и она оказывается совершенно неверной. Это предсказание в вопиющем противоречии с фактами гласит: обмен энергией внутри печки должен приводить к передаче энергии от любой длины волны к более короткой до тех пор, покапрактически вся энергия не окажется в ультрафиолете или еще дальше. Таким образом, на предсказанном графике кривая стремится к бесконечности в области ультрафиолета. Разумеется, эта «ультрафиолетовая катастрофа» не наблюдается у реальных излучателей, от разогретого докрасна железа до ярко-белого Солнца. Они излучают тепло в виде оранжевого света вместо того, чтобы остывать из-за быстрой ультрафиолетовой вспышки. Физики делали повторные попытки вывести экспериментальное энергетическое распределение из обычной волновой теории, уравнений Максвелла и электронной теории. Всех постигала неудача: снова и снова предсказания хорошо совпадали с экспериментом на красном конце спектра, но на другом конце возникала ультрафиолетовая катастрофа. Тогда около 1900 г. немецкий физик Макс Планк подошел к проблеме с другой стороны и спросил, как Эйнштейн в теории относительности (исторически позже. — Перев.): как нужно минимально модифицировать теорию, чтобы согласовать ее с фактами? Он располагал только экспериментальной кривой, но не ее алгебраической формулой, поэтому и не мог с помощью логики найти точную модификацию. Вместо этого Планк обратился к догадкам и предположениям, как в свое время поступил Кеплер. После блестящего умозрительного анализа он нашел успешное правило. Планк заметил, что необходимо некоторое правило, которое бы оставляло красный свет практически неизменным, но подавляло фиолетовое и ультрафиолетовое излучение. Рассмотрим аналогичную задачу в большом бакалейном магазине. Как можно ограничить продажу каких-либо товаров, не повышая цены на них? Можно было бы продавать товары только большими партиями. Например, для распределения в семье денег на покупки не имеет особого значения, что рис, сахар и соль продаются не вразвес, а в пакетах по полкилограмма. Но если сахар упакован в неделимые мешки по 50 кг, то его будут покупать только те семьи, в которых есть сильные руки, большой автомобиль и другие ресурсы. Торговля сахаром в магазине почти прекратилась бы из-за ограничений, наложенных расфасовкой в слишком большие мешки.

Фиг. 175. Излучение энергии из «абсолютно черного» излучателя при различных температурах. (экспериментальные факты).

Суть предположения Планка состоит в том, что энергия излучения упакована маленькими (атомных масштабов) порциями, так называемыми «квантами». Размер квантов не одинаков для разных цветов — они крошечные у инфракрасного, маленькие у зеленого и большие у ультрафиолетового излучения. Как повлияет такая упаковка на предсказываемый спектр излучения? Предположим, радиация выходит из дырки в печке, и рассмотрим обмен энергией между излучением и стенками внутри печки. Квантовые ограничения будут наиболее заметны для ультрафиолетового конца спектра, где кванты велики. Инфракрасный свет будет непрерывно изливаться обильным потоком крошечных квантов, слишком крошечных, хотя и многочисленных, чтобы повлиять на обмен энергией. Но ультрафиолетовый свет должен либо излучаться большими квантами, либо вовсе не излучаться. Голубое, фиолетовое и, особенно, ультрафиолетовое излучение будет существенно подавлено, и тем самым будет предотвращена ультрафиолетовая катастрофа. Более детально правило Планка гласит:

Излучение упаковано порциями («кванты»),

В век атомов вещества, атомов электричества — это естественное предположение, которое следует попытаться проверить.

Каждый квант состоит из излучения единственной частоты (и, следовательно, единственной длины волны, т. е. из света «одного цвета» — из монохроматического излучения).

Правило, определяющее размеры квантов:

ЭНЕРГИЯ КВАНТА ПРОПОРЦИОНАЛЬНА ЧАСТОТЕ ИЗЛУЧЕНИЯ В ДАННОМ КВАНТЕ, ИЛИ ЭНЕРГИЯ = h∙ЧАСТОТА, ИЛИ E = h∙v (и, следовательно, Е ~ 1/λ), где h — универсальная постоянная (теперь ее называют постоянной Планка), a v, как обычно, частота излучения.

Исходя из этого, Планк предсказал распределение энергии в излучении черного тела. Его предсказание совпадает с экспериментальным графиком как в области ультрафиолета, так и в остальных частях спектра. В инфракрасной области формула Планка приводит к традиционным, известным раньше предсказаниям, совпадавшим здесь с экспериментом. Так что это было замечательное предположение для всех областей. Разумеется, оно привело к согласию с экспериментом; в противном случае Планку, как в свое время Кеплеру, пришлось бы выдвигать другие гипотезы. Поразительно, что то же самое правило разрешает и другие, казалось бы, совершенно иные парадоксы.

Фиг. 176. Излучение (факты и теория).

Значение квантовой постоянной h

Универсальная постоянная h в единицах СИ равна 6,62∙10^-34.

Поскольку h = (энергия кванта)/частота, то его размерность дж/сек^-1, или дж∙сек. Таким образом,

h = 6,62.10^-34 дж∙сек.

Планк не угадывал этой величины; она получилась из сравнения с экспериментом. Планк изменял картину излучения от гладкого, непрерывного потока, подобного струе воздуха, до зернистого, подобного струе песка. При большей выбранной величине h и все «песчинки» должны быть большими, а чем больше зернистость, тем больше она ощущалась бы. Если величина h равна нулю, то все «песчинки» слишком малы для проявления, и тогда получается обычное предсказание ультрафиолетовой катастрофы. Если h очень велика, то «песчинки» короткой длины волны должны быть слишком большими, так что их не смогут создать атомы обычной печки, и тогда ультрафиолета вообще не было бы, если только температура не слишком высока. При некоторой промежуточной величине h предсказания прекрасно согласуются с фактами. Подбором получается величина 6,6∙10^-34 дж∙сек.

Величина квантов

Квантовое правило Е = h∙v расфасовывает зеленый свет по маленьким порциям энергии, величиной около 2,5 эв. У красного света — большая длина волны (меньшая частота) и меньшие кванты, 1,8 эв. Кванты голубого света — большие, 3 эв. Это крошечные порции: посмотрите на зажженную свечу в другом конце комнаты, и в ваш глаз будет попадать в секунду около 10 000 000 000 квантов видимого света. При моментальном снимке в фотоаппарате используется примерно 1 000 000 000 000 квантов. Однако десяток голубых квантов может создать пометку на фотопленке, а человеческий глаз настолько чувствителен к ним, что нервы в его сетчатке реагируют чуть ли не на одиночный квант. Продолжая рассмотрение за границы видимой части спектра, мы обнаруживаем инфракрасное излучение, распределенное по очень малым порциям энергии, и радиоволны в настолько маленьких порциях, что вряд ли можно надеяться непосредственно заметить действие (удары) отдельных квантов — но они ясно обнаружены непрямыми экспериментами, где они переворачивают спин атома.

С другой стороны, ультрафиолетовый свет распространяется большими квантами (что-нибудь около 12 эв), рентгеновские лучи излучаются огромными квантами (такими, как 50 000 эв), а γ-лучи — вообще гигантскими квантами (до 10⁶ эв и больше). Поглощение одного большого кванта может изменить ген наследственности в живой клетке и даже убить клетку.

Фиг. 177. Теория излучения (подгонка теории Планка к экспериментальным фактам выбором h).

Квантовая революция

Может показаться: не слишком ли много беспокойства из-за единственного расхождения между теорией и экспериментом? Но это расхождение было жизненно важным, поскольку относилось к спектру излучения каждого нагретого тела (от парового котла до звезд) и показывало, что в теории, скомбинированной из механики, волновой теории света и электронной теории, что-то совершенно неверно. Хотя недостаток был обнаружен макроскопическими экспериментами, Планк проследил его происхождение до атомных масштабов: атомы испускают и поглощают свет атомными порциями энергии (и, по-видимому, он так и должен распространяться).

Ученые консервативны: они отнюдь не стали сразу приветствовать революционные изменения теории, а, напротив, упорно держались за свои старые взгляды как за жизненные принципы. Многих шокировала идея о том, что излучение состоит из «пуль», и они сомневались в том, что правило Планка Е = h∙v дает адекватное и необходимое описание природы. Тогда Эйнштейн защитил правило Планка от враждебного отношения, показав, что оно объясняет также и другие загадки: изменение удельной теплоемкости с температурой и фотоэлектрический эффект. А Пуанкаре дал общее математическое доказательство того, что если требовать согласия с экспериментальными фактами, то излучение должно обладать определенной дискретной упаковкой. Сегодня имеется так много экспериментальных доказательств существования энергетических порций в излучении, что все принимают квантовую точку зрения. Но на многие годы осталась основная загадка: каким образом излучение может быть одновременно и непрерывным потоком волн и градом «пуль»?

Фиг. 178. Величина кванта энергии.

_{Объем изображенного шара показывает энергию одного кванта.}

Удельная теплоемкость[186]

Измеренная удельная теплоемкость простых твердых тел и газов не согласуется с предсказаниями кинетической теории. Эйнштейн и другие авторы попытались применить квантовое ограничение Е = h∙v к тепловой энергии, которая заключена в колебаниях атомов и вращении молекул. Результат: превосходное согласие с экспериментом. Таким образом, квантовое правило распространяется не только на излучение, но и на другие явления: на любое периодическое движение (такое, как колебание или вращение), имеющее определенную частоту. (Кинетическая энергия свободного поступательного движения осталась неквантованной, см. гл. 30.)

Фотоэлектрический эффект

Своего объяснения ожидало от квантовой теории еще одно парадоксальное явление; связанные с ним экспериментальные факты как бы кричали: «Кванты!» Речь идет о фотоэлектрическом эффекте, который в наши дни используется в электронном «зрении» и который, видимо, всегда, хотя и в более сложной форме, использовался в наших собственных глазах. Луч света, падающий на чистый металл, может выбивать из него электроны. Слабый свет выбивает электроны с той же кинетической энергией, что и яркий свет, но просто их число оказывается меньшим. Даже если свет настолько слаб, что вылетают одиночные электроны через минуту или еще реже, все равно они имеют ту же самую скорость. И каким бы слабым ни был свет, электрон никогда не ждет до тех пор, пока он наберет достаточно энергии от столь слабого постоянного потока: иногда он вылетает с полной скоростью сразу, как только будет включен свет; в других случаях он может ждать дольше, чем в среднем это нужно, — и все происходит совершенно случайно. Такого поведения нельзя ожидать, если непрерывный поток волн раскачивает электрон вверх — вниз до тех пор, пока не разорвет его связи, — подобно ребенку в ванне, создающему колебания воды, приводящие к выплескиванию ее через край. Наблюдаемое поведение электронов соответствует скорее свету, излучаемому порциями, подобными кусочкам динамита. Это наиболее прямое подтверждение существования квантов — «зерен» света.

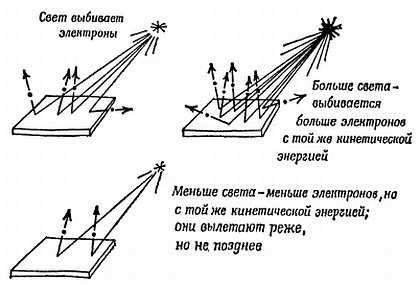
Фиг. 179. Фотоэлектрический эффект.

ДЕМОНСТРАЦИОННЫЙ ОПЫТ 1

Соедините с электроскопом лист чистого цинка, сообщите ему положительный заряд и направьте на него луч белого света. Ничего не произойдет. Повторите то же самое, сообщив цинку отрицательный заряд. Листочки электроскопа опадают: под действием света цинк теряет отрицательно заряженные электроны. Поставьте на пути света лист стекла — заряды больше не будут утекать. Более сложные опыты утверждают: ультрафиолетовый свет — это существенный фактор; утечка заряда происходит из-за того, что электроны выходят, или, лучше сказать, выбиваются под действием ультрафиолета и затем удаляются под влиянием электрического поля заряженной пластины. Если пластина заряжена положительно, то электроны тоже могут быть выбиты, но поле пластины возвращает их обратно. Этот демонстрационный опыт показывает лишь грубые черты эффекта — зернистость света не заметна, если только не использовать очень слабый свет. Но тогда при выбивании одиночных электронов необходимо очень большое усиление (для возможности регистрации эффекта).

Фиг. 180. Демонстрация фотоэлектрического эффекта.

ДЕМОНСТРАЦИОННЫЙ ОПЫТ II

Направьте слабый свет на счетчик Гейгера с прозрачным окошком в его трубке (или дайте возможность попадать туда рентгеновским лучам из удаленного источника). Счетчик будет срабатывать при «вспышке» ионов, порожденной каждым электроном, который выбивается из газа в трубке, — но чтобы эта демонстрация была убедительной, необходимо сделать ее значительно более утонченной.

Фотоэлектроны и цвет света. Частицы, вылетающие с освещенной пластины в вакууме, можно исследовать с помощью электрических и магнитных полей. Оказывается, это обычные электроны с энергией в несколько электронвольт. У натрия и некоторых других металлов эффект вызывается видимым светом, и эти металлы используются в устройствах типа «электронного глаза». У большей части металлов эффект вызывается ультрафиолетовым излучением. Если использовать свет достаточно короткой длины волны, эффект обнаруживается на всех веществах.

Для любого определенного металла и одноцветного света все электроны получают одну и ту же энергию[187] (она равна стандартной энергии, характерной для данного цвета, за вычетом стандартного «налога», выплаченного в виде энергии, за выходэлектрона из металла). Вывод: свет переносит свою энергию стандартными порциями (пакетами).

Фиг. 181. Фотоэлектрический эффект: описание механизма, предложенное Эйнштейном.

Размеры энергетических пакетов для разных цветов должны быть различными. При использовании голубого света энергия появляющихся фотоэлектронов больше, чем при использовании зеленого света; красный свет в большинстве случаев слишком «беден», чтобы внести плату за выход электрона. Ультрафиолетовый свет извлекает электроны с большей энергией, нежели видимый свет. Рентгеновские и γ-лучи дают еще более сильный эффект: они выбивают электроны из любого вещества, хотя часто проходят в веществе длинный путь, прежде чем выберут для этого какой-либо электрон. На снимке в камере Вильсона показаны треки таких «фотоэлектронов», выбитых из молекул воздуха рентгеновскими лучами (см. фиг. 49). Все треки показывают электроны одной и той же энергии — рентгеновские лучи также «зернисты».

Для классической физики такое поведение кажется очень странным. Это примерно так же, как если бы океанские волны, входя в гавань, не могли раскачать корабли, стоящие здесь на якоре, но после того как некоторое время ничего не происходило, один корабль вдруг подпрыгнул бы на 100 м в воздух; снова штиль, потом другой корабль… тоже на 100 м. Вскоре стало ясно, что фотоэффект не может быть спусковым механизмом, в котором свет «освобождает электроны, уже снабженные энергией их будущего движения, поскольку ее величина определяется цветом света. Кто заказывает музыку, тот и должен расплачиваться с музыкантом. Но классическая теория не дает свету такого кармана, из которого он мог бы расплатиться»[188].

Фотоэлектрический эффект продолжал оставаться загадкой до тех пор, пока Эйнштейн не применил к нему квантовую теорию. Пусть энергия падающего света поступает квантами. Один электрон получает целый квант энергии, частично выплачивает ее за то, чтобы ускользнуть от собственного и соседних атомов, и вылетает с остатком (кванта энергии) в виде кинетической энергии.

Предположим, что энергия, необходимая для освобождения электрона, равна Е₀ — это «налог за выход», подобный «налогу» за испарение молекулы из жидкости. Тогда квант света может выбить электрон, если энергия кванта Е больше, чем Е₀. Вылетающему электрону остается

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ = Е — Е₀ = h∙v — E₀.

С этой точки зрения для одноцветного света все фотоэлектроны должны иметь одну и ту же энергию. Для большинства материалов величина Е₀ больше, чем энергия кванта у голубого света, и лишь у ультрафиолетового и рентгеновского излучения энергия кванта может превысить Е₀.

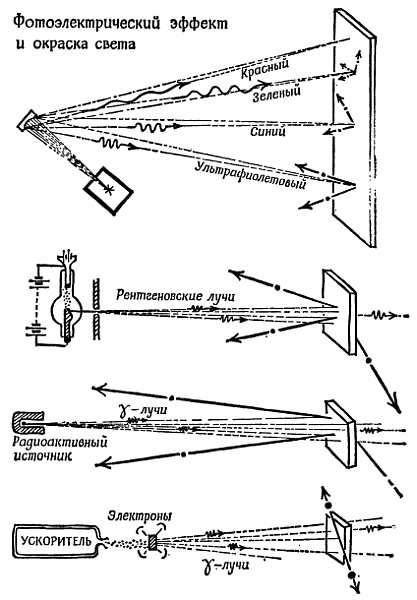
Фиг. 182. Фотоэлектрический эффект и окраска света.

_{Красный свет не может выбить ни одного электрона почти ни из какой поверхности; голубой свет выбивает из некоторых металлов электроны с малой кинетической энергией; ультрафиолетовый свет выбивает электроны с большей кинетической энергией; рентгеновские лучи и γ-лучи выбивают электроны из любого материала с еще большей кинетической энергией. А γ-лучи высокой энергии могут даже отрывать нуклоны от ядер (фоторасщепление).}

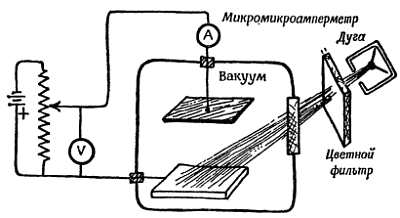
Фиг. 183. Фотоэлектрический эффект и цвет света; аппаратура для измерений.

Для проверки предложенного Эйнштейном соотношения приложим к собирающей пластинке тормозящее электрическое поле, достаточное для того, чтобы электроны, в отсутствие поля достигающие этой пластины, останавливались вблизи нее. Если для этого достаточно разности потенциалов в V в, то выбитые электроны должны были иметь кинетическую энергию (V в)∙(е кулон), или V∙e дж. Поэтому V∙e должно быть равно hv — E₀(Ve = hv — E₀). График зависимости тормозящего напряжения V от частоты v, полученный при использовании света нескольких различных цветов, должен быть прямой линией. Тангенс угла наклона этой прямой должен быть равен

h/e, т. е. ПОСТОЯННАЯ ПЛАНКА / ЗАРЯД ЭЛЕКТРОНА

Задача 1

По-видимому, вы заметили, что раньше в этом курсе использование слова «должен» осуждалось. («Ученые говорят о том, что происходит фактически, а не о том, что должно…») Как вы расцениваете с этой точки зрения использование чуть выше слова «должен» (причем дважды)?

Задача 2

Покажите математически, что тангенс угла наклона должен быть равен h/e.

Милликен провел тщательные измерения с фотоэлектронами из натрия и других веществ. Чтобы уменьшить помехи от различных загрязнений, он обрабатывал в вакууме поверхность чистого металла на маленьком токарном станке с выведенным наружу магнитным управлением! Он не только проверил предсказание Эйнштейна, но даже измерил величину h/e и получил значение h, согласующееся с величиной, которую Планк получил другим путем.

Задача 3. Фотоэлектрический эффект и квантовая постоянная

Измерения Милликена показаны на фиг. 184 [Physical Review, VII, 362 (1916)]. Оцените с помощью этого графика квантовую постоянную h, если известно, что е = —1,6∙10^-19 кулон. Частота света для различных использованных им цветов дана в герцах и вычислена по отношению скорости света к длине волны, которая в свою очередь измерена с помощью дифракционной решетки. Разность потенциалов, указанная на графике, — это наименьшее тормозящее напряжение, которого достаточно для того, чтобы предотвратить попадание на коллектор электронов, выбитых светом. (При нахождении этой разности потенциалов из измеренных им величин Милликен учитывал «э.д.с. батареи», созданной двумя, различными металлами, которые были использованы в качестве фотоэлектрической поверхности и коллектора, но это не влияет на наклон графика.)

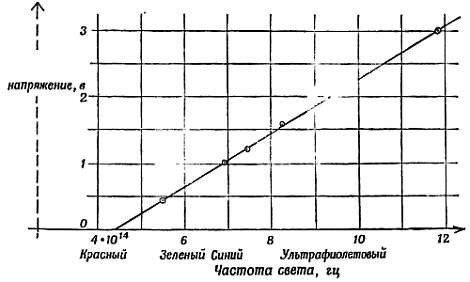
Фиг. 184. Фотоэлектрический эффект: измерения Милликена (к задаче 3).

Соотношение Эйнштейна остается справедливым также для ультрафиолета, рентгеновских и γ-лучей, равно как и для всех веществ. Таким образом, фотоэлектрический эффект ясно обнаруживает квантовые свойства излучения. Видимый свет в лучшем случае лишь слегка щелкает по электронам, ультрафиолетовый свет их выбрасывает, рентгеновские лучи вышвыривают их, а γ-лучи выбивают их прямо-таки, как ударом хлыста. А у γ-лучей очень короткой длины волны кванты настолько велики, что они могут разбить ядро. Вот пример: фоторасщепление дейтрона:

Фактически этот процесс дает хороший способ измерения массы нейтрона. Нужно только найти минимальную энергию, которую должны иметь γ-кванты в этом процессе, и скомбинировать ее с массами водорода и дейтерия, измеренными с помощью масс-спектрографов. Соотношение Эйнштейна применимо также к обратному процессу: быстро движущиеся электроны могут, останавливаясь в мишени, создавать рентгеновские лучи. Чем выше напряжение на пушке, тем больше кинетическая энергия электронов и тем выше максимальная частота образующихся рентгеновских лучей. (Это дает полезное правило, поскольку частота определяет проникающую способность рентгеновского излучения.) Гораздо более медленные электроны могут иногда создавать кванты видимого света, замедляясь при столкновениях.

Фиг. 185. Фоторасщепление дейтрона.

_{Фотон γ-лучей с энергией 2,2 Мэв или больше может разорвать ядро тяжелого водорода на протон и нейтрон.}

Фотоны

Таким образом, в начале этого века была принята квантовая теория с ее единственным правилом: ЭНЕРГИЯ КВАНТА = h∙ЧАСТОТА. Она успешно объяснила спектр излучения, удельную теплоемкость, фотоэлектрический эффект, образование рентгеновских лучей. Планк показал, что при излучении атомов энергия упакована в кванты. Затем Эйнштейн продвинулся еще дальше, показав, что излучение само по себе должно быть упаковано в кванты.

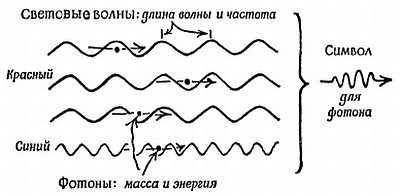
Фиг. 186. Природа света.

Это было в 1905 г. — в том самом году, когда он опубликовал также свою теорию броуновского движения и выдвинул специальную теорию относительности! Таким образом, квантовая теория с помощью Эйнштейна превратилась из правила упаковки в стройное рассмотрение излучения как малых частиц. Чтобы подчеркнуть представление о частицах, всякий раз, когда имеют в виду корпускулярный аспект в поведении излучения, говорят о фотонах (по аналогии с электронами, нуклонами и т. п.). Все фотоны перемещаются (в вакууме или воздухе) со скоростью света с. Тогда, как следует из релятивистской формулы для массы, они должны иметь нулевую массу покоя. Это не вещество, поскольку их никогда нельзя найти покоящимися. При движении они имеют массу m, такую,

что

ЭНЕРГИЯ, m∙с² = ЭНЕРГИЯ, h∙v

и

ИМПУЛЬС = m∙с = ЭНЕРГИЯ/с = h∙v/с

Таким образом, мы представляем излучение как ведомый волнами, перемещающимися со скоростью света с, поток фотонов, каждый из которых переносит массу, импульс, энергию h∙v.

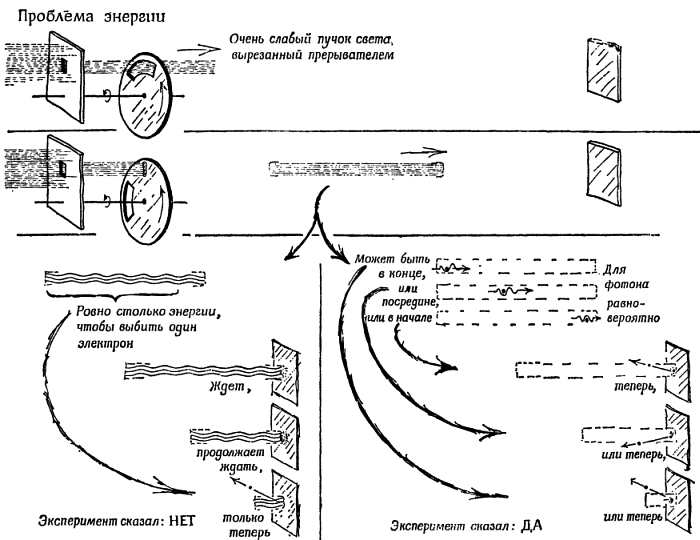
Фиг. 187. Природа света.

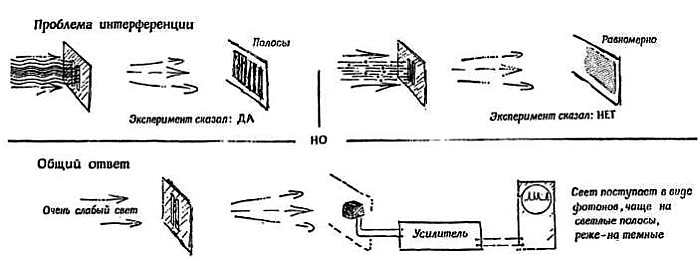
_{В экспериментах проявляются две свойственные свету формы поведения, которые кажутся противоречивыми, но которые можно согласовать следующим путем. Пропускаем свет через «прерыватель» (отбирающий короткие сигналы света) и направляем его на поверхность металла, из которой свет может выбивать электроны. При этом используется настолько слабый пучок света, что если свет представляет собой непрерывный поток волн, то нам всегда придется ждать почти до конца такого сигнала, прежде чем наберется энергия волны, достаточная для вырывания одного электрона. Однако, если свет представляет собой поток частиц, мы ожидаем, что электроны будут испускаться на произвольных стадиях; иногда в конце сигнала, иногда в середине, а иногда при поступлении самого начала сигнала. Такой эксперимент был проделан. Каждый выбитый электрон ускорялся к мишени, где он выбивал большое число электронов в «фотоэлектронном умножителе», который действует как усилитель для одного выбитого электрона. Импульс заряда от этого усилителя наблюдался на осциллографе, развертка которого синхронизирована с прерывателем. Оказывается, импульсы поступают произвольно во все моменты светового сигнала. Посмотрите об этой демонстрации замечательный кинофильм Джона Кинга «Фотоны», сделанный P.S. S. С. (В фильме, который вы увидите, этот вопрос иллюстрирован такой задачей: человек хочет получить литр молока из снабжающего его потока, который поступает через прерыватель. Имеются две формы снабжения; 1) сплошной поток по желобу, при котором человеку приходится ждать определенное время, пока наполнится его литровая бутыль; 2) конвейер, доставляющий ему литровые бутылки, наполненные молоком, — причем они беспорядочно расставлены вдоль конвейера.)}

_{Теперь свет от одного источника будем пропускать через две щели и посмотрим, какая картина получится на удаленном экране. Если свет представляет собой потек частиц, то в том месте экрана, куда попадает свет от обоих источников, должно быть сплошное светлое пятно. Если же свет — непрерывный поток волн, то на экране должны быть интерференционные полосы. Фактически мы видим полосы — интерференционные полосы Юнга. Но если наблюдать, как поступает энергия в интерференционные полосы, то можно обнаружить, что она поступает в частицах (квантах или фотонах). На светлые полосы поступает много фотонов, тогда как на темные — очень мало. Итак, мы можем сказать, что свет состоит из частиц, ведомых волнами при образовании интерференционной картины. (См. другой превосходный фильм Р. S. S. С. «Интерференция фотонов», снятый Джоном Кингом.)} 

Столкновения фотонов с электронами. Комптон-эффект

Поскольку фотоны переносят импульс, они должны оказывать давление на поглощающую стенку, а на полностью отражающую стенку — удвоенное давление. Оказывается, это в самом деле так. Измерение очень малого давления пучка света было выполнено[189] и подтвердило выражение для импульса Е/с. Если фотоны представляют собой компактные частицы, обладающие импульсами, то значения этих импульсов должны изменяться при столкновениях с другими частицами, такими, скажем, как электроны. Так и происходит. Фотоны рентгеновского излучения отклоняются при столкновении с электронами, слабо связанными в некоторых атомах, и уходят в новом направлении с меньшей энергией и, стало быть, большей длиной волны. Электроны же отскакивают с соответствующей частью первоначальной энергии фотона, и их короткие следы отдачи можно увидеть в камере Вильсона. Такой «эффект отдачи» открыл А. X. Комптон, и его измерения согласуются с предсказаниями для таких столкновений между «частицами». (Разумеется, для предсказаний нужно использовать релятивистскую механику, поскольку фотоны движутся со скоростью света.) Этот эффект дает одно из лучших доказательств того, что фотоны представляют собой частицы, которые подчиняются механическим законам сохранения и при столкновениях с частицами вещества могут передавать одновременно энергию и импульс.

Атом «действия», h

Постоянная Планка h — это универсальная «атомная» постоянная. Подобно скорости света, ее величина не изменяется при преобразованиях теории относительности — она одинакова для всех наблюдателей. Это не атом энергии. Это атом отношения энергия/частота или же произведения энергия∙период, или же произведения энергия∙время, которое называется «действием». Если вы подумаете, то сообразите, что в ньютоновской механике действие имеет вид произведения: сила∙расстояние∙время.

Глядя на это выражение, можно предположить, что такая величина вполне может обладать полезными свойствами. Это в самом деле так. Законы Ньютона и многие другие законы физики можно переформулировать такими словами: «Снаряды, планеты, электроны, световые волны, — все физические объекты выбирают для своего движения такой путь, чтобы действие было или минимально, или максимально, — говоря математическим языком, принимало экстремальное значение. Природа ведет себя так, как будто ей нежелательно, чтобы действии оказалось чуть меньше или больше».

Фиг. 188. Эффект Комптона.

_{Фотон рентгеновского излучения, столкнувшись со слабо связанным атомным электроном, уходит с меньшей энергией (большей длиной волны); электрон испытывает отдачу.}

АТОМ БОРА-РЕЗЕРФОРДА, 1915–1925 гг.

Резерфордовская модель атома имела успех — она способствовала размышлениям и экспериментам, — но парадокс оставался. В атоме вокруг ядра существует поле, убывающее по закону обратных квадратов (что было доказано рассеянием альфа-частиц), а электроны остаются в этом поле далеко от ядра (это также было подтверждено рассеянием альфа-частиц, а позднее спектрами рентгеновских лучей). Поэтому: 1) электроны не могут покоиться в состоянии устойчивого равновесия (теорема Ирншоу). Атомы не разрушаются, излучая при этом электромагнитные волны; следовательно, 2) электроны не могут находиться в движении по эллиптическим кеплеровским орбитам. Утверждения 1) и 2) противоречат друг другу. Далее, иногда атомы излучают; они испускают свет. Световое излучение раскаленного газа расщепляется на очень резко определенные цвета, спектральные «линии» определенной длины волны и частоты колебаний. Частоты излучений возбужденных атомов весьма определенно сгруппированы в несколько серий, характерных для атомов каждого элемента. К 1905 г. были известны общие формулы для спектральных серий, а измеренные частоты некоторых серий расшифрованы с помощью простого закона, для которого теория не могла предложить удовлетворительного объяснения. По-видимому, этот простой закон каким-то образом учитывал квантовые ограничения, поскольку дело касалось фотонов, (Каждая спектральная линия представляет собой свет одного цвета, одной частоты, поэтому она должна представлять собой поток фотонов с одинаковой энергией.) Этот простой закон содержит постоянную, которая оказывается одинаковой для многих спектров. Если бы удалось получить эту универсальную константу спектров, комбинируя другие общие постоянные, такие, как заряд электрона е, скорость света с, постоянная Планка h и т. п. (и подбросив им на помощь числа типа π, 2 или √2), это было бы очень приятным открытием. А если бы при этом еще мощно было привести ясные теоретические аргументы в пользу выбора именно такой комбинации, то это было бы великим открытием. В этом направлении было много попыток и заявлений об успехе — ученые от Пифагора до Кеплера и позже вплоть до нынешних дней искали золотое правило, которое бы объединило вместе наиболее важные числа; результаты этих поисков простирались от бессмыслицы до знаменитых открытий. Бор не только нашел такую комбинацию для постоянной спектра, но и обосновал ее, что принесло ему прочную славу.

Атом Бора. Правила

В 1913 г. смелый и неизвестный молодой датский физик Нильс Бор предложил минимальные изменения классической физики, с помощью которых можно объяснить факты и, комбинируя которые, сделать замечательные предсказания. Обратившись к парадоксу со стабильностью атомов, которые должны были бы быстро коллапсировать[190], он предложил следующие новые правила:

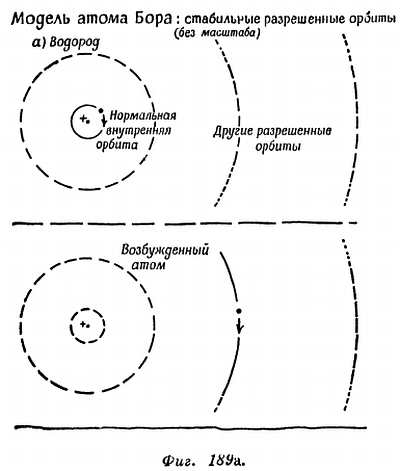
ПЕРВОЕ ПРАВИЛО. Атомы построены в соответствии с моделью Резерфорда, но электроны движутся по стабильным орбитам без излучения. (Хотя этим заявлением противоречие было только подтверждено, но его ясное признание уже было большим утешением.)

ВТОРОЕ ПРАВИЛО. Разрешены только некоторые орбиты. Эти стабильные орбиты определяются по квантовым правилам следующим образом. У электрона, движущегося по стабильной орбите, действие должно всегда быть равным h, или 2h, или 3h…, nh…[191]. Имеем

ДЕЙСТВИЕ = ЭНЕРГИЯ ∙ ВРЕМЯ,

= [СИЛА ∙ РАССТОЯНИЕ] ∙ ВРЕМЯ,

= [СИЛА ∙ ВРЕМЯ] ∙ РАССТОЯНИЕ,

= ИМПУЛЬС ∙ РАССТОЯНИЕ.

Для круговой орбиты, например, мы смело берем в качестве расстояния длину окружности и пробуем проверить правило:

ИМПУЛЬС ∙ (ДЛИНА ОКРУЖНОСТИ) = h,

или 2h, или 3h…

Вообще, mv∙2πR = nh, где n = 1 соответствует низшей разрешенной орбите, n = 2 — следующей и т. д. Квантовое число n должно быть целым числом.

На модель атома в виде солнечной системы таким образом накладываются жесткие ограничения: разрешены лишь определенные орбиты, а именно только такие, на которых ДЕЙСТВИЕ равно nh, где n — целое число.

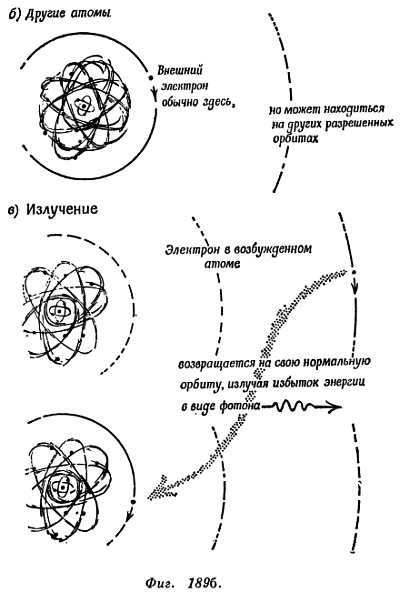
ТРЕТЬЕ ПРАВИЛО. Один из электронов атома можно переместить (например, при бомбардировке) на свободную внешнюю орбиту, так что получится «возбужденный» атом с большей энергией. Затем электрон может перескочить с внешней орбиты на свободную внутреннюю. Когда это происходит, атом испускает избыток энергии в виде кванта света.

h∙ЧАСТОТА ИСПУЩЕННОГО СВЕТА = ИЗБЫТОК ЭНЕРГИИ ЭЛЕКТРОНА=

= ЭНЕРГИЯ ЭЛЕКТРОНА на «внешней» орбите — ЭНЕРГИЯ ЭЛЕКТРОНА на «внутренней» орбите

Атом Бора. Плодотворная теория

Бор сохранил резерфордовскую картину атома, в котором электроны мчатся по орбитам вокруг ядра, притягивающего их с силой, обратно пропорциональной квадрату расстояния. Поэтому «диаграмму холма» для их энергии (диаграмму потенциальной энергии) нужно было бы изображать по-прежнему. Как и в случае настоящей солнечной системы, эта диаграмма для сил притяжения изображает яму вместо холма. Но второе правило квантовых ограничений Бора как бы вырезает уступы вдоль стен ямы и ограничивает орбиты этими уступами. На фиг. 191 показан набросок «диаграммы холма» для Солнца, вокруг которого по круговой орбите движется одна планета, а другая описывает эллипс. Этот «холм» был хорош для сил притяжения к Солнцу.

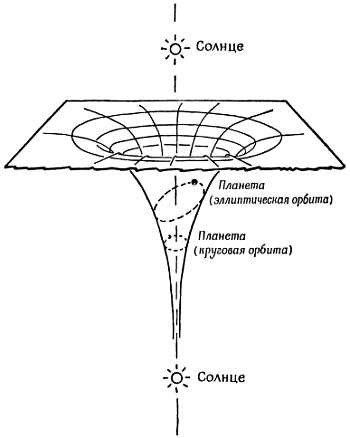
Фиг. 191. Энергетический холм (яма).

_{Диаграмма для солнечной системы (из книги К. Mendelsshon, What is Atomic Energy, Sigma Books, Ltd.).} 

Аналогичной была бы «диаграмма холма» для ядра и электронов в «атоме Резерфорда без квантовых ограничений». На фиг. 192 показана упрощенная «диаграмма холма» атома с набором «квантовых уступов» для круговых орбит. В схеме Бора были учтены также другие уступы (уровни энергии), отвечающие эллиптическим орбитам. Форма, размеры и другие характеристики каждой орбиты были определены несколькими квантовыми числами.

Фиг. 192. Энергетический холм (яма).

_{Диаграмма для модели атома Бора (из книги К. Mendelsshon, What is Atomic Energy, Sigma Books, Ltd.).}

Низший уступ, определенный по квантовым правилам Бора значением n = 1, дает наименьшую разрешенную орбиту. Здесь энергия электрона минимальна; эта орбита наиболее стабильна, поэтому можно было бы ожидать, что электрон будет падать вниз до этого уровня, если только это возможно, и останется здесь. Действительно, следовало бы спросить: почему же не все электроны падают на этот нижний уступ, а все атомы не сжимаются до минимальных размеров? Мы знаем, что так не происходит, и это была одна из многих тайн, которые вскоре объяснились правилом, сформулированным В. Паули под названием принципа исключения[192]. Здесь принцип в сущности утверждает, что на уступе может находиться лишь один электрон, только один электрон с данным набором квантовых чисел. Никогда, ни в каком атоме несколько электронов не могут занимать совершенно одинаковые орбиты. Теперь, правда, мы удваиваем каждый выступ, чтобы поместить туда два электрона с противоположными спинами. С помощью современных знаний можно обосновать принцип Паули, однако долгое время он оставался произвольным, но очень полезным руководством для моделей атома.

В сущности Бор сказал: «Электроны не могут непрерывно излучать; атомы не подчиняются традиционным законам физики. Если вы примете мое смелое предположение, факты обретут больше смысла». А Паули добавил ограничительное правило: «Только один электрон на орбите». Эти правила выглядят как законодательство, основанное на декретах, но они успокаивают волнение, вызванное парадоксами атомной модели, обогащая знания. Они дали Бору возможность вычислить универсальную постоянную спектра, исходя из фундаментальных компонент е, h, с, e/m, и плодотворно объяснили все спектры, которые вскоре после объяснения перешли в разряд решенных проблем, и осветили другие нерешенные проблемы. Еще когда Бор продолжал развивать свои правила, Мозли использовал их в грубой теории спектров рентгеновских лучей, что позволило ему измерить атомные номера, — почти перед этим стал понятен смысл атомного номера с точки зрения строения атома, содержащего ядро.

Правила Бора, например, предсказывают диаметр обычного атома водорода, который уже был экспериментально известен из грубых измерений.

Размеры атома водорода

Общие размеры атома водорода определяются диаметром орбиты 2r единственного электрона, вращающегося вокруг ядра атома (в модели Бора). Два атома, удаленные на расстояние больше 2r, будут нейтральными друг для друга и не смогут взаимодействовать с большой силой. При расстоянии между атомами меньше 2r орбиты их электронов окажутся перекрывающимися, и здесь должны возникнуть нарушения, приводящие к притяжению, а при еще меньших расстояниях — к отталкиванию[193]. Таким образом, величина 2r должна определять «диаметр» атома при слабых столкновениях и, возможно, при образовании молекул. Экспериментальные оценки (грубые из длины молекулы масла и хорошие из данных о внутреннем трении в газообразном водороде) показывают, что «диаметр» атома водорода немного больше 1 А° (10^-10 м). Ниже показано, как Бор вычислил величину 2r с помощью своих квантовых правил.

Квантовое правило Бора mv∙2πr = nh для электрона на самой низшей, наиболее стабильной орбите с n = 1 даст mv∙2πr = h, или mv = h/2πr. Электроны удерживаются на своих орбитах в атоме притяжением заряда ядра Ze, которое обратно пропорционально квадрату расстояния, так что

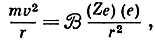
причем для водорода Z = 1.

Используем алгебру, чтобы исключить отсюда орбитальную скорость электрона и найти радиус орбиты через h,  и т. п.:

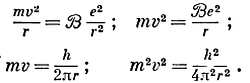
Разделив первое равенство на последнее, получим

т. е. радиус орбиты равен

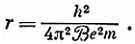
Используем экспериментальные значения:

h (по Планку или Милликену)… 6,62∙10^-34 дж∙сек;

 (из измерений силы, действующей на заряд в электрическом поле)… 9,00∙109 ньютон∙м²/кулон²;

е (Милликен)… — 1,60∙10^-19 кулон;

m (из значения е по Милликену и e/m по отклонению заряда в полях)… 9,11∙10^-31 кг.

Тогда

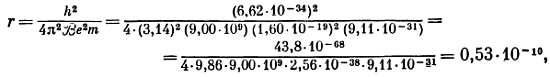
а в качестве размерности для r получается

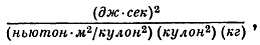
что сводится к метру.

Здесь было приведено предсказание Бора для размеров атома водорода, полученное математически. Посмотрите на исходные величины:

h — постоянная Планка для квантов излучения;  — постоянная в законе Кулона; е и m — заряд и масса электрона. Вывод: диаметр электронной орбиты в невозбужденном атоме водорода 1,06∙10^-10 м, или ~ 1 A°; «размер атома», в хорошем согласии с прямыми измерениями.

Бор и спектры — электронные гармоники?

Крупнейшим достижением теории Бора было предсказание ею спектра излучения раскаленного водорода. Этот линейчатый спектр был другим парадоксом, нуждавшимся в объяснении, — экспериментальные формулы требовали простой теории. Если раскаленные добела твердые вещества излучают сплошной спектр «черного тела», то пылающие газы (разогретые или возбужденные электрическим разрядом) дают совершенно иной спектр. Анализ их излучения показывает, что в спектре отсутствует свет большей части цветов, а имеются лишь очень узкие и очень яркие полоски определенных цветов, т. е. спектр состоит из ярких «линий», каждой из которых соответствует практически одна длина волны (см. гл. 10). У каждого газа есть свой характерный набор линий: красная линия (и много других) у неона; желтая (и несколько ультрафиолетовых) у паров натрия (которые можно получить, поместив поваренную соль в пламя) и т. д. Длины волн ярких спектральных линий имеют вполне определенную величину для атомов каждого элемента. Они дают первоклассный способ анализа любых материалов — будь то образцы промышленных изделий или газы в далеких звездах. Линии каждого элемента группируются вдоль спектра в правильные серии с переменным шагом. С помощью выполненных в прошлом веке тщательных измерений длин волн было рассортировано много таких серий. В расположении каждой серии явно наблюдается некоторая система. Для водорода и некоторых других газов из измерений было получено очень простое основное правило, отражающее такую систему.

Фиг. 193. Получение и анализ спектров.

Если белый свет из раскаленного твердого тела проходит через холодный газ, то мы можем наблюдать «спектр поглощения»: полный спектр белого света с черными линиями, в которых свет отсутствует, при длине волны, на которой газ излучал бы свет, если бы он был раскален. Эти линии поглощения можно использовать для анализа атмосферы вокруг «твердых» звезд, в том числе и нашего Солнца, в спектре белого света у которых наблюдаются темные линии, характерные для водорода, паров натрия, кальция и т. д. Эти линии, очевидно, получаются из-за того, что атомы более холодного газа поглощают свет, который соответствует их «собственным колебаниям»[194]. Они должны затем снова испускать точно такой же свет, но уже во всех направлениях, так что линия выглядит темной по сравнению с другими цветами, которые приходят непосредственно из более горячей «сердцевины» звезды. Эти факты снова наталкивают на мысль о некотором механизме колебаний, способном реагировать на волны определенной частоты.

Фиг. 194. Эскизы спектров.

_{Эти черно-белые эскизы — только тусклая имитация. Взгляните на реальные вещи: посмотрите на неоновую вывеску через призму или дифракционную решетку; держите блестящую швейную иглу на солнце и рассматривайте ее через призму, которую следует держать близко к глазам, — вы увидите фраунгоферовские линии поглощения. (В реальных спектрах линий обычно гораздо больше, чем изображено здесь. Относительная яркость линий зависит от условий возбуждения атомов.)} 

Далее, было ясно, что атомы, возбужденные бомбардировкой или электрическим полем, могут колебаться и испускать волны света с различными частотами. Есть ли сходство между этими собственными «естественными частотами» атома и колеблющейся струной? Струна арфы или скрипки может колебаться с любой частотой из некоторой серии в соответствии с тем, что стоячая волна имеет одну пучность или 2, 3, 4… пучности. Тогда частоты находятся в той же самой пропорции, т. е. 1:2:3:4:…, а издаваемые музыкальные ноты имеют соответствующие частоты.

Для струны теория согласуется с экспериментом. Второй закон Ньютона предсказывает серию:

ЧАСТОТА = (постоянная К)∙(n),

где n = 1, 2, 3… Частоты света разных цветов в спектре атома водорода образуют почти столь же простую серию, формула для которой (из эксперимента) имеет такой вид:

ЧАСТОТА = (постоянная К)∙((1/2²) — (1/n²))

где n = 3, 4, 5… для последовательных линий серии. Точные измерения[195] с помощью высококачественной дифракционной решетки дали значение

К = 3290 000 000 000 000.

Бор предсказал эту формулу с постоянной К, равной

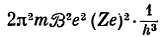
(см. следующий раздел). При использовании измеренных величин h, е, m и Z = 1,  = 9,00∙10⁹ эта формула дает

К = 3 286 000 000 000 000.

В более полной форме предсказание Бора выглядело так:

v = K∙((1/n_f²) — (1/n_i²))

где n_f — «конечное» квантовое число для орбиты, на которую «падает» электрон, одинаковое для всех линий серии, а n_i означает «начальное» квантовое число другой орбиты, с которой «падает» электрон.

Видимой серии для водорода соответствует n_f = 2 и n_i = 3, 4, 5…

Задача 4

Две другие серии для водорода были уже известны, а еще две были открыты позднее там, где их предсказал Бор. Посмотрите на приведенную выше общую формулу и предскажите формулу для серии в ультрафиолетовой области с большими квантами и для серии вблизи инфракрасной области.

Другие элементы после возбуждения также дают линейчатые спектры, если они находятся в газообразном состоянии. При расшифровке большинства линейчатых спектров можно использовать почти ту же самую константу К, а остальная часть формулы имеет довольно похожую алгебраическую форму. Поэтому с точки зрения предположений Бора все линейчатые спектры приобретают следующий смысл: каждая линия образуется в результате того, что электрон «перепрыгивает» с одной разрешенной орбиты (или «уровня») на другую, испуская разность энергий в виде кванта света этой спектральной линии. Сами по себе орбиты, определенные квантовыми правилами, стабильны: электрон может оставаться длительное время на одной из них, не излучая. В этом причина того, что (холодный) газ не светится до тех пор, пока его не облучат. Излучение испускается лишь при изменении орбит. Поэтому, чтобы электрон мог испускать свет, он должен сначала двигаться по внешней орбите, т. е. находиться на высоком энергетическом уровне и иметь возможность «упасть» на низший уровень. И в этом же причина того, что атомы газа испускают резкие спектральные линии, каждая из которых имеет определенную длину волны, поскольку получается при переходе между определенными орбитами. Таким образом, спектры создаются возбужденными атомами. Ион (атом, потерявший электрон), получая обратно потерянный электрон, может испускать одну или последовательно несколько линий, когда этот электрон «падает» с одного энергетического уровня на другой.

Сегодня понятие «стабильные орбиты» звучит слишком категорично, но мы будем использовать лишь их существенное свойство — определенность энергии на каждой из них — и поэтому будем говорить об «уровнях энергии».

Так Бор преобразовал спектроскопию, которая была эмпирической схемой исследования газов, в важное средство изучения атомной структуры.

Фиг. 195. Размещение линий спектров по шкале частот.

_{а — проанализированный по сериям спектр гелия; б — видимые серии атомарного водорода.}

Спектроскопическая постоянная по Бору. Примите на веру или вычислите сами

Предсказание постоянной К требует математических выкладок для вычисления энергии электрона в поле ядра. Примите на веру результаты таких выкладок, приведенные на математической схеме (фиг. 196), или проследите за приведенными ниже вычислениями.

Фиг. 196. Схема математических расчетов для атома Бора.

Нам нужно знать энергию электрона для квантовых чисел n = n_i и n = n_f. Тогда мы сможем предсказать частоту измеряемого фотона, поскольку

h∙v излучения = ΔE = ΔE_i — ΔE_f.

Электрон, движущийся по орбите, имеет энергию Е, складывающуюся из кинетической энергии (К. Э.) и потенциальной энергии (П. Э.) (которая равна энергии, накопленной в электрическом поле системы электрон + ядро). Перенесем электрон из бесконечности на расстояние r от ядра с зарядом Ze. Он притягивается ядром, поэтому при сближении электрона с ядром энергия переходит от электрического поля к электрону (в виде кинетической энергии).

При изменении расстояния х между электроном и ядром на величину dx из электрической потенциальной энергии в кинетическую энергию передается величина

F∙dx, или

Это уменьшение потенциальной энергии атома, т. е. энергия, реализованная из накопленного запаса. (Здесь эта величина положительна, поскольку как F, так и dx отрицательны: F — притяжение внутрь, a dx — смещение внутрь, уменьшение х.) Очевидно, наибольшую потенциальную энергию электрон имел на бесконечности, когда его отвели наиболее далеко от притягивающего ядерного заряда, и он по дороге туда накопил потенциальную энергию. Поэтому, если считать потенциальную энергию электрона на бесконечности равной нулю, то вблизи ядра она должна быть отрицательной.

Потенциальная энергия электрона, перенесенного из бесконечности на орбиту радиусом r, равна

что после интегрирования дает

0 — ∙(e)∙(Ze)/r

Таким образом, потенциальная энергия электрона равна

П.Э. = — ∙(e)∙(Ze)/r

Поскольку при орбитальном движении

— mv²/r = ∙(-e)∙(Ze)/r² (знак минус показывает направление силы внутрь),

то

П.Э. = —∙(e)∙(Ze)/r = —mv² = — (2 x К.Э.)

Полная энергия

Е = К.Э. + П.Э. = ¹/₂ mv² + (—mv²) = — ¹/₂ mv²

Нам нужно знать выражение для энергии Е (через квантовое число n и другие постоянные), не содержащее v или r. Воспользуемся соотношением для орбитального движения

— mv²/r = ∙(-e)∙(Ze)/r²

и исключим r с помощью квантового правила mv∙2πr = nh:

mv² = ∙(e)∙(Ze)/r

mv = nh/2πr

Разделив первое равенство на второе, получим

v = ∙(e)∙(Ze)∙(2π)/nh

Тогда

Подставим n = n_i для начального и n = n_f для конечного уровней, между которыми переходит электрон, и получим

Откуда спектроскопическая постоянная

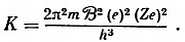
При подстановке измеренных значений е, e/m, h,  и для водорода Z = 1 эта формула дает превосходное согласие с величиной K, полученной экспериментально из измерений спектров, а именно 3,286∙10¹⁵ в сравнении с 3,290∙10¹⁵.

Дальнейшие предсказания

Предсказания Бора можно продолжить. Предположим, атом гелия потерял один из двух своих электронов, а оставшийся электрон испускает свет при переходе между орбитами. Тогда ионизованный атом гелия с одним оставшимся электроном подобен атому водорода с двойным зарядом ядра +2е. Для Z = 2 предсказываемые частоты излучения ровно в 4 раза больше частот излучения водорода (см. формулу Бора для К). Такие линии были уже открыты в спектре гелия при искровом разряде и ошибочно приписывались водороду в каком-то необычном состоянии. Бор не только указал, что они исходят от однократно ионизованного гелия, но, используя входящую в предсказание малую поправку на конечность массы ядра, оценил отношение массы электрона к массе протона и получил 1/1830.

Кроме того, формула Бора для водорода, примененная к переходам внутренних электронов в тяжелых атомах, предсказывает частоту рентгеновского излучения, которая много больше частоты видимого света, поскольку постоянная К содержит[196] множитель Z². Это позволило Мозли сравнить атомные номера (Z) различных элементов, находя квадратный корень из частоты рентгеновского излучения от соответствующей мишени. Это был первый простой способ измерения атомных номеров. Атомы любого элемента могут излучать несколько серий, причем формулы, связывающие частоты соответствующих линий из разных серий имеют вид арифметических разностей. Бор сразу объяснил эти соотношения, приписав все спектральные линии переходам с одних энергетических уровней на другие. Каждая серия относится к определенному конечному уровню энергии. Тогда вычитание частоты одной линии из другой дает разность между энергиями двух верхних уровней, и эту разность можно получить несколькими вычитаниями (фиг. 197). Бор смог также вычислить «энергию ионизации» атома водорода, т. е. энергию, необходимую для полного удаления электрона из атома. По его предсказаниям эта величина равна 13,54 эв[197]. Трудный эксперимент — бомбардировка атомарного водорода электронами — дал значение 13,6 эв.

Используя измеренные спектры частот рентгеновского излучения и видимого света, Бор изобразил энергетические уровни атомов всех элементов и построил схему строения атома, объясняющую периодическую систему химических элементов. В его схеме электроны вращаются по определенным окружностям (или эллипсам), образующим группы, или оболочки. Это была довольно удачная схема. Она «объяснила» общие химические свойства элементов и даже предсказала свойства одного неизвестного элемента и помогла его открыть (речь идет о гафнии).

Плодотворность теории подтвердила объявленные Бором правила; но они оставались произвольными правилами без обоснований.

Фиг. 197. Уровни энергии в воровской модели атома (упрощенно).

Основа уверенности Бора. Принцип соответствия

Все же эти правила были не совсем произвольными, поскольку Бор прежде всего сохранил надежную связь с прежней теорией. Рассмотрим некоторый предельный случай, когда квантовые ограничения становятся несущественными. Здесь предсказания, которые делает новая теория, должны совпадать с предсказаниями старой, классической теории. В тех местах, где старый теоретический материал оказывается непригодным при объяснении фактов, его нужно вырезать; но новый материал, который используется для того, чтобы залатать брешь или расширить целое изделие, на краях должен вплетаться в старую ткань.

Принцип соответствия: в той области, где различия между предположениями старой и новой теории несущественны, обе теории должны перекрываться и находиться в согласии друг с другом. Такое утверждение кажется очевидным, но оно служит мощным направляющим правилом для новых предположений. Это общее правило подойдет для любой науки, для каждой хорошей теории.

Примеры вы уже встречали:

правила теории относительности сводятся к обычной геометрии и механике при малых скоростях (в предельном случае, когда множитель √(1 — v²/с²) ~= 1.

Формула Планка для излучения черного тела в длинноволновой области согласуется с классическими предсказаниями (в предельном случае, когда кванты малы и их много).

Второй закон Ньютона F = M∙a сводится к первому закону Ньютона, если тело движется с постоянной скоростью (в предельном случае а = 0).

Законы Кеплера для эллиптических орбит согласуются с более простой теорией для круговых орбит (в этом предельном случае).

Думающий читатель сумеет распространить принцип соответствия дальше: на изобретение или критику новых теорий из области геометрии, развития популяций, промышленных циклов управления, этики…

Поэтому Бор постулировал, что квантовые правила для орбит должны накладывать все меньше ограничений при увеличении квантового числа. Для орбиты с n, равным, скажем, 1000, переход на соседнюю орбиту должен тогда сопровождаться лишь малым процентным изменением величины «действия» электрона (равному произведению импульс∙длина окружности). Дискретность действия, требуемая квантовой теорией, должна быть несущественна. До перехода и после него электрон должен иметь почти одну и ту же частоту обращения, а частота, которую может иметь испущенный свет, совпадает с этой почти неизменной частотой обращения электрона — как этого и требует классическая теория. В этом предельном случае больших n правила Бора действительно приводят к согласию со старой теорией. Потребовав соответствия, Бор смог найти нужное новое правило mv∙2πr = nh; но хотя принцип соответствия помогает выбрать верное правило, однако не дает его обоснований. И все-таки Бор и другие ученые, выдвигая замечательные предположения новой теории, продолжали требовать такого «соответствия», или согласования в той области, где новая теория встречается со старой.

Трудности

Эта плодотворная теория испытывала трудности трех видов:

а) Она оказалась не в состоянии детально предсказать спектры других атомов (кроме водорода); она не могла объяснить химические силы и строение молекул.

б) В руках людей, рассуждающих менее осторожно, чем Бор, модель обрела черты реальности. Орбиты стали четко очерченными в пространстве — на обложках некоторых книг их так и продолжают изображать! Ученые забыли предостережение Эйнштейна: не украшать теорию деталями, которые нельзя проверить. Нам никогда не удается увидеть орбиты. Их можно сконструировать, только предположив, что применимы макроскопические (большего масштаба) правила планетарной солнечной системы. В действительности известно лишь то, что у атомов есть определенные уровни энергии и что при переходах между уровнями испускаются и поглощаются фотоны.

в) Более того, квантовое правило Бора для выбора орбит или уровней по-прежнему не имело правдоподобного объяснения, и не было никаких причин электронам оставаться на орбитах, не излучая.

Дальнейшее применение этой теории, как это случается со многими другими хорошими теориями, обнаружило ее слабость.

Для спасения теории ее нужно было модифицировать, и вскоре это было сделано. Изменение теории было радикальным и началось с экстраординарного предположения, которое сделал французский физик Луи де-Бройль.

ЧАСТИЦЫ И ВОЛНЫ

Новая теория

«Давайте будем рассматривать электроны подобно световым волнам, — предложил де-Бройль. — Хотя это частицы вроде снарядов, но они являются также и волнами».

Свет имеет два типа свойств, которые кажутся прямо противоположными: волновые свойства и свойства снарядов (частиц). Разумеется, во многих отношениях оба типа свойств приводят к одинаковым результатам. Свет распространяется по прямой линии с определенной скоростью, он переносит энергию и импульс, оказывает давление на поверхность тел; его лучи отражаются и преломляются (искривляются) на границе различных материалов. Все это может происходить и с потоком снарядов, и с вереницей волн. Но имеется и существенная разница.

СНАРЯДЫ (частицы) ∙ ВОЛНЫ

С: ПЕРЕНОСЯТ СВОЮ ЭНЕРГИЮ (КИНЕТИЧЕСКУЮ ЭНЕРГИЮ) И ИМПУЛЬС КОМПАКТНЫМ ПАКЕТОМ

В: ПЕРЕНОСЯТ СВОЮ ЭНЕРГИЮ, РАСПРЕДЕЛЕННУЮ ПО ВСЕМУ «ФРОНТУ ВОЛНЫ»

С: ПРИ НАЛОЖЕНИИ ДВУХ ПОТОКОВ ИХ ВКЛАДЫ ПРИБАВЛЯЮТСЯ ОДИН К ДРУГОМУ:

В: ПРИ НАЛОЖЕНИИ ДВУХ ПОТОКОВ (ИЗ ОДНОГО ИСТОЧНИКА) ИНТЕРФЕРИРУЮТ

С: СНАРЯДЫ + СНАРЯДЫ = БОЛЬШЕЕ ЧИСЛО СНАРЯДОВ

В: ВОЛНЫ + ВОЛНЫ = БОЛЬШЕ ВОЛН В ОДНИХ МЕСТАХ, НО В ДРУГИХ МЕСТАХ ВОЛНЫ ОТСУТСТВУЮТ

С: ОТБРАСЫВАЮТ РЕЗКУЮ ТЕНЬ

В: ОГИБАЮТ ПРЕПЯТСТВИЯ

С: либо ПРОХОДЯТ через ДЫРКУ В СТЕНКЕ, либо НЕ ПРОХОДЯТ — СНАРЯД НЕ МОЖЕТ ПРОЙТИ ЧАСТИЧНО ЧЕРЕЗ ОДНУ. А ЧАСТИЧНО ЧЕРЕЗ ДРУГУЮ ДЫРКУ В ОДНОЙ И ТОЙ ЖЕ СТЕНКЕ

В: МОГУТ ПРОХОДИТЬ С ОДНОЙ СТОРОНЫ СТЕНКИ НА ДРУГУЮ ЧЕРЕЗ ЛЮБОЕ КОЛИЧЕСТВО ДЫРОК. ПОПЕРЕЧНЫЕ ВОЛНЫ МОГУТ ОБЛАДАТЬ ПОЛЯРИЗАЦИЕЙ

Свет и любое другое электромагнитное излучение обладают свойствами, указанными в обоих колонках таблицы. Слабый свет звезд выбивает фотоэлектроны, отдавая всю свою энергию, куда бы он ни попал. Но, собирая тот же самый свет линзами огромного телескопа, можно получить интерференционную картину, в которой виден весь широкий фронт волны.

Рентгеновские лучи также выбивают фотоэлектроны, полностью передавая им свою энергию, а когда они рассеиваются на атомах, каждый квант отскакивает от некоторого электрона и точно так же, как это сделал бы снаряд, передает ему малый импульс отдачи (эффект Комптона, фиг. 188). Но при рассеянии рентгеновских лучей на кристаллической решетке, образованной слоями атомов, получается гладкая, коллективная картина интерференции; подобно световым волнам, у них также проявляется поляризация. Так что теперь мы описываем свет, рентгеновские лучи и т. п. как фотоны, снаряды энергии и импульса, ведомые вдоль своих траекторий волной; отчасти это соответствует давнишнему предположению Ньютона.

Де-Бройль сделал свое «возмутительное» предположение: припишем реальным снарядам (частицам) такие же волновые свойства. Если наделить каждую частицу вещества сопровождающей ее волной с неизвестной фазой, некоторой длиной волны и скоростью перемещения, то это позволит электрону, атому, любому движущемуся объекту образовывать интерференционную картину! Тогда мы должны сказать, что в некоторых отношениях электрон ведет себя как волна (ЯВЛЯЕТСЯ волной). В других случаях он ведет себя как частица (ЯВЛЯЕТСЯ частицей). Когда де-Бройль написал свое предположение в виде короткого поразительного письма в общедоступный научный журнал, многим казалось, что он почти сумасшедший. Со временем это принесло ему Нобелевскую премию.

Ниже приведен его рецепт рассмотрения, основанный на том, что для света уже приняты и корпускулярное, и волновое представления. Воспользуемся связывающим их квантовым правилом, чтобы выразить длину волны через характеристики частиц:

Определим теперь длину волны λ частицы вещества точно так же:

ДЛИНА ВОЛНЫ = h/ИМПУЛЬС = h/mv

Тогда частица, обладающая большой массой и обычной скоростью, будет иметь настолько малую длину волны λ, что эффектами интерференции и дифракции можно пренебречь, — винтовочная пуля должна лететь по прямой, а не осыпать мишень со всех сторон частями интерференционно-дифракционной картины. Но у малых частиц, таких, как электрон, должны проявляться волновые эффекты. Подобно рентгеновским лучам, электроны из трубки с разностью потенциалов 50—100 в должны иметь длину волны, сравнимую с расстоянием между атомными плоскостями в кристаллах. Дэвиссон и Джермер из лаборатории, принадлежащей компании «Белл телефон», наблюдали «волны электронов», облучая маленький кристалл никеля потоком электронов[198]. К тому времени, когда де-Бройль высказал свое предположение, они уже обнаружили, что электроны, вместо того чтобы рассеиваться в широком интервале направлений, отдают предпочтение некоторым из них, что весьма загадочно для поведения частиц. Затем, приняв предположение о волнах, они проделали тщательные измерения: электроны из пушки с напряжением 54 в, которыми облучали кристалл никеля, интенсивно рассеиваются на угол 50° по отношению к отраженному назад пучку, а на все другие углы, кроме угла рассеяния назад, — очень слабо.

Фиг. 198. Электроны как волны: опыт Дэвиссона и Джермера.

Задача 5. Волны электронов?

а) Рассчитайте длину волны де-Бройля для «54-вольтовых» электронов по следующей схеме: кинетическая энергия электрона равна энергии, полученной его зарядом при прохождении разности потенциалов 54 в.

Вычислите:

1) скорость электрона v (пользуйтесь обычной механикой, поскольку он движется медленно по сравнению со светом. Возьмите е/m = 1,8∙10¹¹ кулон/кг);

2) его массу m (Используйте значения е/m и е. Возьмите е =1,6∙10^-19 кулон);

3) его импульс mv;

4) его длину волны λ. (Возьмите h = 6,6∙10^-34 дж∙сек, или (м)∙(кг∙м/сек).)

Ответ к вопросу 4 получится в метрах. Выразите его также в ангстремах (10^-10 м).

б) Повторите контрольные расчеты Дэвиссона и Джермера. По измерениям с рентгеновскими лучами им было известно, что расстояние между слоями атомов в их кристалле никеля составляет 2,15 А°. Волновая теория предсказывает, что для волн с длиной волны λ, падающих на дифракционную решетку с постоянной d, дифракционный максимум приходится на угол А, который определяется из соотношения d∙sin A = λ. (Как в случае рентгеновских лучей, в случае электронов сильный дифракционный максимум создают несколько слоев атомов, отражающих волны совместно в одной и той же фазе. Тем не менее можно все же использовать приведенную выше формулу для плоской решетки, выведенную в гл. 10. Но там d означало расстояние между штрихами решетки, здесь — расстояние между рядами атомов кристалла. При таком расчете для получения максимума дифракционного пучка требуется точно такая же длина волны, как и при полном трехмерном рассмотрении.)

1) Вычислите К для волн, которые дают дифракционный максимум под углом 50° при рассеянии на кристалле с межатомным расстоянием 2,15∙10^{- 10} м (sin 50°= 0,766).

2) Сравните полученный результат с предсказанной вами в пункте а) «длиной волны» использованных электронов.

Измерения показали, что интерференционная картина соответствует длине волны λ = h/mv. Одновременно аналогичная проверка была проведена в Англии Г. Томсоном. С тех пор проводилось много измерений аналогичных дифракционных картин для потоков электронов, протонов, атомов и даже нейтронов. Эти картины показывают, что частицы движутся в направлении распространения волн. Волны сообщают нам, где мы сможем обнаружить частицы, [Никаких исключений в этом отношении мы не ожидаем. Убедившись в волновом поведении атомов, мы считаем, что оно свойственно также бейсбольным мячам и винтовочным пулям, но грубые оценки их длин волн даже при медленном движении показывают, что они (длины волн) слишком малы, чтобы их можно было измерить или как-либо заметить любые волновые эффекты.]

Наиболее яркую демонстрацию волновых эффектов придумал Г. Мёлленштедт. Он натянул чрезвычайно тонкую проволоку поперек пучка электронов, вылетающих из пушки. На удаленной фотопленке, регистрирующей поток, образуется тень проволоки. Затем проволоке сообщается малый положительный заряд. Электрическое поле этого заряда отклоняет поток электронов, проходящих по обе стороны от проволоки, поэтому тень исчезает, а вместо нее появляется «яркое» пятно в том месте, где перекрываются два потока, проходящих с двух сторон проволоки. В этом пятне видны полосы Юнга — места, где

«электроны + электроны = больше электронов»,

и другие места, где

«электроны + электроны = нет электронов».

В темных полосах отнюдь не происходит взаимного уничтожения электронов — просто они не могут туда попасть, поскольку волновая природа уводит их куда-нибудь в другое место. Эта техника весьма трудна — картину нужно увеличить линзами электронного микроскопа, — но результаты великолепны.

Посмотрите на фиг. 199–202 и сравните картину, образованную электронами, и аналогичную картину для световых волн.

Фиг. 199. Волны из двух когерентных источников образуют интерференционные полосы.

Фиг. 200. «Бипризма» из стекла преобразует источник света в два источника так, что создаются световые интерференционные полосы.

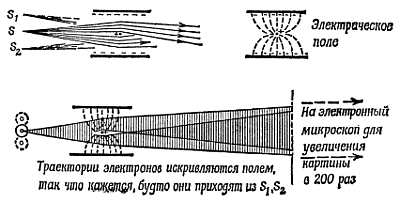
Фиг. 201. Эксперимент Мёлленштедта.

_{Для электронов электрическое поле возле положительно заряженной проволоки действует как «бипризма». Как и для фотонов, имеются «яркие» полосы в тех местах экрана, куда попадает много электронов, и «темные» полосы, куда попадает мало электронов, — направляющие «волны материи» создают интерференционную картину. Картина настолько мала, что ее приходится увеличивать линзами электронного микроскопа, а затем еще увеличивать с помощью оптики.}

Фиг. 202. а — интерференционная картина, образованная видимым светом (увеличено в 30 раз).

_{Фотографию сделал Генри А. Хилл из Принстонского университета;}

б — интерференционная картина, образованная электронами (увеличено в 5000 раз).

_{Фотография Г. Мёлленштедта и X. Дюкера из Тюбингенского университета. Эксперимент опубликован в журнале «Zeitschrift fur Phisik», том 145, 1956.}

Сложный конфликт

Идею дуализма «волна — частица» трудно воспринять для света, но еще труднее — для атомов, электронов и всех кусочков вещества. Свет, проходящий через пару щелей в стенке, образует на удаленном экране интерференционные полосы Юнга. Но его энергия, очевидно, переносится пулеподобными квантами, большая часть которых попадает на яркие и лишь малое число квантов — на темные полосы. Если через две щели проходит поток электронов[199], снова получается интерференционная картина, так что каждый индивидуальный электрон должен каким-то образом пройти через обе щели[200]. Его волна должна проходить через обе щели, иначе как же получится интерференционная картина? Но как это может сделать пуля?

Волновые пакеты

По отношению к этому парадоксу де-Бройль выдвинул некоторые утешительные соображения — но его аргументы сложны и требуют математики в большей мере, чем мы здесь дадим, Его идея состояла в следующем: представлять волны, соответствующие фотонам или частицам вещества, как компактную группу мелких волн, подобную всплеску на воде, который можно создать одиночным шлепком по поверхности воды в ванне или бассейне.

Проследите, как такая группа волн распространяется по воде; вы увидите, что она с определенной скоростью v расплывается как кольцо возмущения. Теперь понаблюдайте за деталями такой группы при ее распространении. Она содержит маленькие волны, перемещающиеся медленнее, чем вся группа в целом. Маленькие волны позади передовой группы непрерывно погибают, тогда как на фронте группы рождаются новые волны. Эта идея группы волн, обладающих различными скоростями, составляет суть схемы де-Бройля. Электроны и световые кванты (фотоны) представляют собой группы волн, компактно переносящие энергию и импульс.

То, что мы обычно наблюдаем как «частицу» (электрон, протон, фотон…), — это «волновой пакет» (см. фиг. 272 ч. I). Однако «всплески» внутри него образованы многими близкими длинами волн, которые собираются вместе, создавая результирующую картину. Эти наборы волн находятся в фазе вблизи центра группы, а переходя в другие места, они взаимно погашаются. Но каждую индивидуальную волну-составляющую можно рассматривать как простирающийся далеко вперед и назад «путепровод». Это волна, которая приводит частицу-пакет к светлой полоске в интерференционной картине. Волны, ведущие частицу, перемещаются быстрее, чем вся группа в целом, в противоположность волнам на воде. Импульс частицы с массой m и скоростью v равен mv; ее волновой пакет перемещается сгрупповой скоростью v, волнам пакета соответствует длина волны h/mv. А сами волны перемещаются со скоростью V, большей v. В действительности V∙v = c², так что V даже больше с. Это не противоречит теории относительности, поскольку V — только скорость перемещения фазы волны, а не скорость распространения энергии. Вы можете представить себе волны, которые бегут впереди частицы, чтобы разметить интерференционную картину и сообщить частице, куда ей следует идти. Загадка дуализма «волна-частица» при этом сохраняется, но все же легче совместить идею волны с частицей, если говорить, что «то, что вы обычно наблюдаете как частицу, представляет собой компактный пакет волн (волновой пакет)» (взгляните снова на фиг. 272 ч. I).

Идея де-Бройля не только объяснила эксперименты, в которых у электронов и других частиц обнаруживается волновое поведение, но и с совершенно неожиданной стороны осветила модель Бора. А затем привела к великому развитию современной атомной теории.

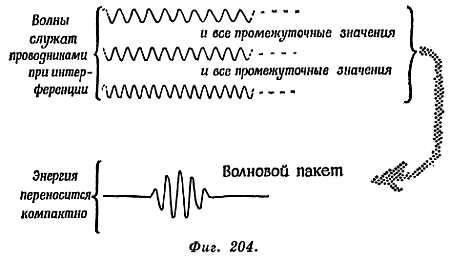
Волны и атом Бора

Де-Бройль прояснил причину загадочного правила mv∙2πr = nh, установленного Бором для разрешенных орбит. Описывающий такую орбиту электрон имеет длину волны λ = h/mv, так что mv = h/λ. Тогда правило Бора приводит к соотношению (h/λ)∙2πr = nh, или 2πr = nλ. С этой точки зрения стабильными являются только такие орбиты, на которых длина волны электрона укладывается целое число раз (n): 2πr₁ = λ₁, 2πr₂ = λ₂, 2πr₃ = λ₃ и т. д. Электрон должен, так сказать, вплетать свою волну туда, где она уже есть (подобно змее, глотающей свой собственный хвост), и образовывать стоячую волну (см. гл. 10) с целым числом длин волн на окружности[201] (фиг. 206). Тогда мы уже видим не твердую частицу с центростремительным ускорением v²/r, которая должна была бы излучать, а волновую картину, заполняющую орбиту. Для многих физиков такая картина давала но крайней мере удобное объяснение произвольного правила Бора: «разрешенные орбиты» соответствуют допустимым стоячим волнам.

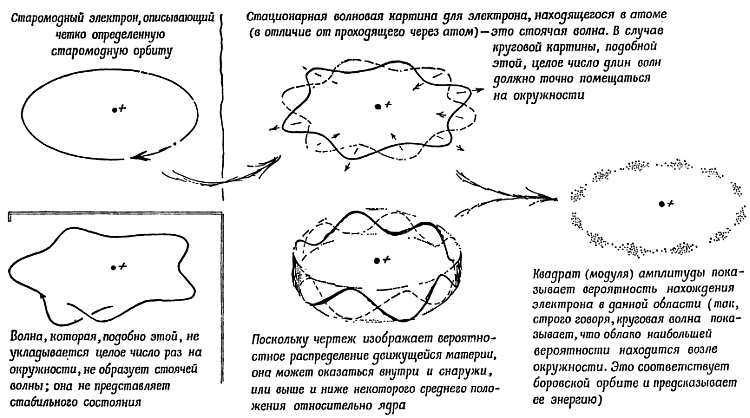
Фиг. 206. Модель атома Бора, в которой электроны заменены волнами де-Бройля.

Теперь мы рассматриваем эти волны де-Бройля как схему, которая сообщает нам о возможном местонахождении электрона: чем сильнее[202] волна в какой-либо области, тем вероятнее, что мы обнаружим там электрон. Эти волны — бегущие волны для движущихся свободных электронов или стоячие волны для электронов, связанных в атоме, — не есть волны движущегося вещества или переменного поля — это «волны вероятности». Кольцевые волны, предложенные впервые для объяснения боровских орбит, могут определять вероятность местонахождения электрона в некоторой области возле окружности. Либо они могут быть эквивалентны волнам, бегущим навстречу друг другу по кольцу. Тогда уже бесполезно спрашивать, в какой точке окружности расположен электрон. В настоящее время для указания вероятности местонахождения электрона мы имеем другие волновые картины для разных состояний: радиальные и круговые стоячие волны. Первая боровская орбита атома водорода заменена радиальной кривой, показывающей интенсивность волны и доходящей до самого ядра. Хотя большую часть времени электрон проводит на разных расстояниях от ядра, среднее расстояние совпадает с предсказанным ранее Бором. А если эту кривую симметрично покрутить по всем направлениям, она изобразит для электрона облако вероятности, рассеянное вокруг ядра. Волновые картины для более сложных атомов и для более высоких энергетических состояний показывают более сложную форму облака. Каждая картина изображает только облако вероятности местонахождения электрона, но частота волнового движения для данной картины является определенной, а это означает определенность уровня энергии электрона.

Такая точка зрения объясняет, в частности, почему атом не может сжиматься так, чтобы электроны двигались по все меньшим и меньшим орбитам. Если положение каждого электрона действительно описывается стоячей волной, то на длине окружности наименьшей орбиты должна укладываться ровно одна длина волны — немыслимо, чтобы в кольцевой стоячей волне содержалась только часть длины волны, — которая должна определить минимальный размер, до которого можно сжать атом. (Соответствующее ограничение для простейшей стоячей волны остается справедливым и при замене циркулярных «орбит» более общими картинами.)

Некоторый смысл приобретает и принцип Паули: посадите несколько тождественных электронов на одну и ту же «орбиту» — картины их стоячих волн сложатся в одну-единственную картину, и тогда мы можем ожидать, что обнаружим один электрон вместо нескольких[203].

Новая атомная теория

Мощный аппарат был развит Шредингером. Исходя из дебройлевского квантово-волнового постулата, он составил общее волновое уравнение (см. т. 2, стр. 588) для электронов. Затем он посмотрел, какие решения в форме стоячих волн должны соответствовать полю кулоновских сил, меняющихся по закону обратных квадратов внутри атома. Это аналогично следующему: определить скорость волны вдоль натянутой струны (см, гл. 10: СКОРОСТЬ² = НАТЯЖЕНИЕ / МАССА НА ЕДИНИЦУ ДЛИНЫ); подставить ее в общее волновое уравнение (²V = (1/c²)∙(d²V/dt²)); наложить «граничные условия», как, например, для жестко закрепленной струны длиной L (закреплены концы, что предотвращает движение в точках х = 0 и x = L); затем найти частоты возможных стоячих волн (как в гл. 10, где вычислены частоты для 1 пучности, 2 пучностей и т. д.). В случае, который рассматривал Шредингер, частоты по квантовому правилу дают энергии. Волновые уравнения и граничные условия здесь более сложны, чем для струны, но они приводят к ценным результатам.

Эта новая интерпретация вскоре была математически применена к волновому рассмотрению электронов в атомах, которое далеко превосходит в успешных предсказаниях теорию Бора. Как и рассмотрение Бора, оно оказалось успешным в применении к атому водорода, даже с более тонкими деталями, и, сверх того, в применении к сложным атомам. Рассмотрение перераспределения электронов при химических превращениях в волновом описании также дало правильные предсказания. Волновое описание было успешно распространено на ядерную физику и интерпретировало радиоактивность в терминах волн-частиц, которые просачиваются через потенциальный барьер ядра. Все это — ценой отказа от какой-либо наглядно определенной модели или картины. Картина атома Бора содержала необязательные конкретные детали — недоказуемые экспериментально и, следовательно, недопустимые для любой долговременной научной теории. Теперь четкие орбиты исчезают и заменяются математическими формулировками волновой модели, которые дают определенные уровни энергии, в точности соответствующие энергиям электронов на старых боровских орбитах. Но у нас нет картины соответствующих волн. Кроме математической формулировки, у них нет ничего общего с волнами на воде или с волнами света. В нашем новом рассмотрении используются такие волны, интенсивность которых показывает, где с наибольшей вероятностью должен быть электрон. Интенсивность волны в выбранной области показывает, сколько шансов за то, что здесь находится электрон. Об интерферирующих световых волнах мы говорим, что математическое описание сообщает нам шансы того, что фотон попадает в определенную часть картины: самые низкие шансы соответствуют темной полосе, самые высокие — светлой. Для связанных электронов в стабильных состояниях атомов у нас есть утверждение о стоячих волнах, которые описывают только облако вероятности распределения электронов: наиболее вероятно здесь, вероятно там, менее вероятно во всех других местах.

Точно так же облако вероятности имеется внутри радиоактивного ядра, например для группы нуклонов α-частицы: вероятность того, что α-частица находится внутри, велика, но, так как волны вероятности распределены во всем пространстве, у α-частицы имеются некоторые шансы оказаться снаружи. В один прекрасный момент она воспользуется этими шансами; тогда она уже снаружи, и после этого электрическое поле выбрасывает ее вдаль. Это грубое, вульгаризованное «объяснение» радиоактивности.

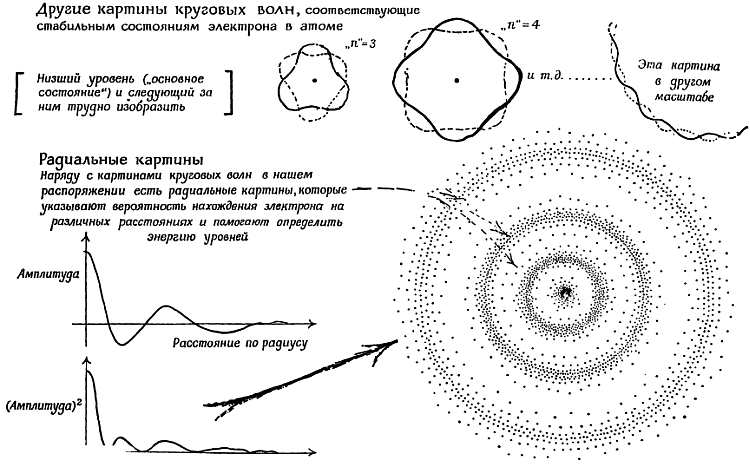
Фиг. 207. Другие волновые картины атомных моделей.

Фиг. 208.

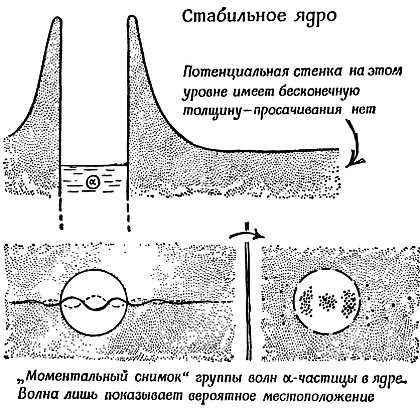
Фиг. 209. Волновые картины в ядрах.

Новое рассмотрение атомов оказалось точным, но отнюдь не простым. При более детальной разработке идея о волнах становится более плодотворной, но сами волны от этого не становятся более реальными. Для их описания мы имеем хороший математический аппарат, но не имеем модели для интерпретации результатов. По существу модели оказались обреченными на неудачу, поскольку они часто вводят в заблуждение. Наша картина атомов и их поведения осталась математической моделью — сложной моделью с зацепляющимися друг за друга частями, которая приводит к плодотворным результатам. Поэтому мы вверяем атомную теорию математикам. Они развили новые средства, например сложную алгебру с нетривиальными правилами[204]. Несмотря на странность методов, результаты превосходны и во всех перечисленных ниже пунктах подтверждаются экспериментальными проверками:

Волновой формализм дает для сложных атомов уровни энергии и вероятности нахождения электрона на каждом уровне; это приводит к успешным предсказаниям частот спектральных линий и их яркостей.

При описании молекул как комбинации атомов волновой формализм предсказывает химические энергии и силы поверхностного натяжения. Он даже предсказывает углы и расстояния между атомами в длинных молекулярных цепях, что подтверждается измерениями с помощью рентгеновских лучей.

Вычисленные вероятности нахождения электрона в некоторой области определенного атома согласуются с измерениями рассеяния потока электронов на атомных электронах в мишени из таких атомов.

Кинетическая энергия α-частиц сообщает нам их длину волны. Это дает вероятность их просачивания через ядерный барьер, что позволяет с определенным успехом предсказать период полураспада радиоактивного ядра.

Но нам приходится оставить аппарат всей этой плодотворной теории в математической форме: мы не можем предложить хорошей модели, в которой все казалось бы «разумным». Мы возвращаемся к детской аргументации «потому что это так» или к взгляду древних греков «это в природе вещей». Как и у древних греков, у наших физиков-атомников есть четкие правила — правила квантования и симметрии, правила, которые работают, — но для них нет первопричины. Сформулировав несколько правил, сказать: «Здесь записано, как ведет себя природа», — вместо того, чтобы во всем обвинять сотни демонов разных мастей, — это все-таки хорошая наука. С этих пор люди, работающие сейчас в физике, оказались разделенными на занимающихся теорией и занимающихся экспериментом. Экспериментатор продолжает исследовать, проверять предсказания, искать новые явления, часто с помощью большой дорогостоящей аппаратуры, для своих непрямых атак на субмикроскопический мир атомов и ядер. Физик-теоретик использует надежные математические методы, избегая думать на языке моделей, к которым склонны более практичные умы. Среди тех и других мы находим великих мыслителей и мудрейших ученых, которые могут объединять теорию и эксперимент и продвигать вперед наше понимание природы.

Принцип неопределенности

Если движение электрона представляет собой распространение его собственной волны, то при желании точно зафиксировать его положение возникает такое же затруднение, как и в случае камеры-обскуры со слишком малым отверстием. Стреляйте пучком электронов через узкое отверстие в стенке: узкий пучок пройдет через него. Но сделайте-ка отверстие еще меньше, такое, чтобы его диаметр по величине сравнялся с длиной волны электрона: пучок прошедших электронов разойдется во все стороны. Он обязан так сделать. Это не есть отклонение, вызванное ближайшими атомами стенки, от которого можно избавиться: это происходит вследствие волновой природы электрона. Попробуйте предсказать, что произойдет дальше с электроном, прошедшим за стенку, и вы, как ни странно, оказываетесь бессильными. Вам точно известно, в каком месте он пересекает стенку, но сказать, какой при этом импульс в поперечном направлении он приобретет, вы не можете. Наоборот, если вы желаете точно определить его импульс и с уверенностью утверждаете «он появится с импульсом mv в первоначальном направлении, вот и все», то для этого вы должны увеличить отверстие настолько, чтобы электронная волна проходила прямо, лишь слабо расходясь во все стороны из-за дифракции. Но тогда вы точно не знаете, в каком же месте электрон-частица прошел через стенку: отверстие-то широкое. Насколько выигрываешь в точности определения импульса, настолько проигрываешь в точности, с какой известно его положение.

Предельную точность, нам доступную, можно найти из соотношения λ = h/mv. Из общей теории распространения волн следует, что если волна проходит через отверстие диаметром, равным λ, или меньше, то она при этом полностью расходится во все стороны; волна же, прошедшая через отверстие диаметром несколько десятков длин волн или еще больше, проходит практически не расходясь (см. гл. 10). Если зафиксировать положение движущейся частицы у стенки с точностью до нескольких длин волн λ, то при этом есть риск сообщить ей в поперечном направлении импульс, составляющий большую, но неизвестную часть от его первоначального, направленного вдоль его движения импульса mv. Если же достаточно знать положение частицы грубо, с точностью до нескольких десятков длин волн λ, то за счет такой жертвы ее конечный импульс будет известен с точностью до величины, составляющей малую часть начального импульса.

Фиг. 210.

Приводимая ниже таблица содержит утверждения, выглядящие более строгими, чем они есть на самом деле, однако в ней приведены результаты полного исследования с учетом детальной геометрии волн.

Это грубые утверждения относительно точности нашего знания. Однако детальное рассмотрение приводит к тому же самому выводу: в каждом случае произведение неопределенностей равно λ∙mv, т. е. (h/mv)∙(mv) = h.

(НЕОПРЕДЕЛЕННОСТЬ КООРДИНАТЫ Δx)∙(НЕОПРЕДЕЛЕННОСТЬ ИМПУЛЬСА Δ(mv)) ~= (КВАНТОВАЯ ПОСТОЯННАЯ h)

Эти неопределенности отвечают разным измерениям: неопределенность одного измерения приводит к появлению неопределенности в другом. Чем точнее производится одно измерение, тем с меньшей точностью можно предсказать результат другого измерения. Неопределенность возникает не вследствие плохой аппаратуры: она лежит в самой природе. Процесс измерения одной величины обязательно ухудшает возможности точного измерения другой. Так как каждая из этих неопределенностей отражает неточность нашего знания, то последнее обязательно в какой-то степени является неточным. Поэтому не следует говорить, что произведение (Δx)∙(Δmv) точно равно h, скорее следует говорить, что оно примерно равно h или «порядка h».

Это и есть принцип неопределенности Гейзенберга. Он сыграл исключительно важную роль при построении математического аппарата для описания волн-частиц в атомах. Его строгое толкование в опытах с электронами таково: подобно световым волнам электроны сопротивляются любым попыткам выполнить измерения с предельной точностью. Этот принцип меняет и картину атома Бора. Можно определить точно импульс электрона (а следовательно, и его уровень энергии) на какой-нибудь его орбите, но при этом его местонахождение будет абсолютно неизвестно: ничего нельзя сказать о том, где он находится. Отсюда ясно, что рисовать себе четкую орбиту электрона и помечать его на ней в виде кружочка лишено какого-либо смысла.

Еще более кардинальные изменения вносит принцип неопределенности в философское мировоззрение. Нельзя получить знание с предельной точностью, которую мы желаем, причем дело тут вовсе не в разуме, терпении, технике или деньгах. Мысленно можно построить сверхмикроскоп для наблюдения электрона. Будет ли тогда уверенность, что координаты и импульс электрона одновременно измеримы? Нет. В любом таком микроскопе для наблюдения должен использоваться тот или иной «свет». Вообще, чтобы «увидеть» электрон, в таком сверхмикроскопе на электроне должен рассеяться хотя бы один квант «света». Такое столкновение приводило бы к изменению движения электрона, вызывая непредсказуемое изменение его импульса (комптон-эффект). И для того, чтобы точно определить местоположение электрона, «свет» должен быть исключительно короткой длины волны, иначе его дифракционное изображение размоется. Поэтому этот квант должен быть исключительно коротковолновым, крайне высокочастотным: это должен быть гигантский квант, фотон γ-лучей. Но в таком случае столкновение будет сильным и импульс отдачи электрона окажется весьма неопределенным. Подробные вычисления на основе соответствующих выражений для импульса отдачи в комптон-эффекте и теории дифракции света в микроскопе дают (Δx)∙(Δmv) ~= h

Подобным же образом этот объективно существующий закон неопределенности работает в случае энергии и времени. Нельзя абсолютно точно измерить кинетическую энергию частицы за бесконечно малый отрезок времени. Неопределенность нашего знания энергии ΔЕ и интервала времени ее измерения Δt связаны следующим образом:

ΔЕ∙Δt ~ h[205]

Во всех приведенных выше соотношениях неопределенностей даже знак ж является слишком точным. Следует говорить (Δx)∙(Δmv) ~ h (примерно такой же величины, как h). Но даже в такой формулировке это лучшее, на что можно надеяться. Поэтому следует говорить «примерно такой же величины, как… или больше[206]».

Этот малый квант действия h играет роль как бы площади дыр в той частой сети, с помощью которой мы желаем выловить информацию в природе. «Клетка точности» вокруг какого-либо куска информации, который мы хотим поймать, должна иметь площадь большую, чем h, иначе улова не будет. Пытаясь поймать какую-нибудь подробную информацию, можно растянуть нашу сеть в каком-нибудь одном аспекте и сузить ее дыры, однако при этом дыры станут длиннее в другом отношении. Подробность, если можно так выразиться, узкая в «ширину», должна быть достаточно велика в «длину», иначе она ускользнет через дыры. Нельзя измерить точно и одновременно величину импульса и координаты: можно только точно измерить одну из них, однако за счет ухудшения знания о другой.

Отсюда ясно, что аппаратура экспериментатора и направление его поиска жестко определяются вопросом, который он изучает. Решив осуществить какое-либо измерение, он тем самым теряет надежду узнать результат точного другого измерения. Это утверждение не звучит как обычное извинение начинающего профессионального ученого: «экспериментальная ошибка», или «вероятная ошибка ± столько-то процентов для данного прибора». Это есть результат всегда существующего, неустранимого взаимодействия прибора и наблюдателя.

На подобное ограничение в биологии уже давно было обращено внимание Г. Дж. Уэллсом: зоолог, экспериментирующий с живым организмом, никогда не имеет дело с абсолютно здоровым, нормальным экземпляром, поскольку сам акт экспериментирования приводит к изменениям в организме исследуемого существа. Современные биологи и те, кто занимается опросом населения, а также все психологи сталкиваются с аналогичным эффектом.

Это ограничение точности физических экспериментов оставалось неосознанным, пока экспериментаторы имели дело с большими телами, состоящими из большого числа атомов. Для таких тел статистические средние (которые мы, жалкие экспериментаторы, обычно наблюдаем) сглаживают флуктуации и дают нам величины, удовлетворяющие строгим законам[207].

Вы уже встречались с эффектом такого сглаживания в случае постоянного давления. Подумайте, однако, что если бы физические эксперименты могла проводить бацилла, то она дала бы совершенно иное описание природы: поверхностные силы перевешивали бы силы гравитации, броуновское движение было бы всеобъемлющим, фотоны бы действовали поодиночке или попарно. Если бы мы могли сами непосредственно это наблюдать, можно было бы еще надеяться видеть и предсказать эти иррегулярности, но при переходе к еще меньшему масштабу — масштабу отдельного атома — присущая природе связь неопределенностей действовала бы в полную силу и препятствовала бы нашему настойчивому любопытству.

Неопределенность и корпускулярно-волновая природа

Если в некоторый момент времени точно замерить местоположение электрона, то это уничтожит все шансы точно измерить его скорость. Это в новой формулировке отражает свойственный природе дуализм волна — частица. Если решено точно измерить скорость электрона, то это позволит определить его импульс и длину волны, важную характеристику последней. Длина волны электрона находится путем измерения длинной последовательности волн (длинного цуга волн), что отрезает путь к рассмотрению электрона в виде компактной частицы и, следовательно, его положения. Если, наоборот, определяется его положение, то тем самым подразумевается, что электрон — частица, и оставляется в стороне вопрос о его волновой природе, что уничтожает возможность что-либо сказать об его импульсе. (См. фиг. 272 из ч. I, иллюстрирующую это.)

Это не безнадежное противоречие между человеком и природой (до этого далеко!): это всего лишь результат наших попыток навязать не свойственное природе обличье. На микроскопическом уровне атомы, электроны и кванты реально ведут себя не как волны и не как частицы. Если в поведении объекта стараться видеть корпускулярные черты, так как что-то в нем их нам напоминает, то это означает измерение характеристик, которыми электрон и атом обладали бы, если бы они действительно были частицами. Человек всегда пытался рисовать себе богов в человеческом обличье. Теперь же он пытается навязать атомам образы его собственных развлечений: мячей, капель воды, океанских волн…

Принцип дополнительности

На основании ранних экспериментов и упрощающих предположений были сформулированы законы Ньютона, уравнения Максвелла, теория относительности, которые довольно хорошо описывают поведение больших движущихся масс, зарядов и т. д. Затем было предположено, что эти представления годятся и для электронов, ядер, квантов… Точнее, поскольку непосредственный контакт с микромиром отсутствует, люди предпочли применить в этой области макроскопические законы, не зная, подходят ли они или нет, и затем вынуждены получать следствия. Теперь мы видим, что неразумно спрашивать, верны или нет эти законы. Можно предположить, что они верны, и тогда мы получаем взгляд на природу, открывающийся в этом предположении (если спросить: «Насколько шторм свиреп?», то можно ответить — «Очень свирепый». Но было бы неразумно отсюда заключить, что у штормов есть характер). Что бы ни представлял собой микромир в действительности — а это «в действительности» может само по себе быть макрочеловеческой ошибкой, — это не есть мир волн или частиц. Втиснутый в рамки волнового описания вопросом о волнах мир дает волновой ответ и игнорирует частицы. Или, будучи спрошенным о частице, он дает ответ, игнорирующий волновую природу частиц. Но это не природа, которая вешает занавес перед фактами о частице, когда ей задают вопрос о волновой природе. Это всего лишь наши вопросы, которые принуждают рядиться не-волну-не-частицу — электрон в неудобную волновую одежду или в одинаково не подходящую ей одежду частицы. Фактически волновая картина использует «для корректного описания не электрон, а состояние знания об электроне»[208].

Люди достаточно умны, чтобы не задавать переполненные предположениями вопросы слишком грубо, однако сознают, что в тех случаях, когда два противоречащих друг другу описания могут быть по отдельности пригодными, то

а) описания взаимно дополняют друг друга: каждое из них «верно», если интересоваться одним определенным свойством материи;

б) описания взаимно исключают друг друга: если используется одно из них, нечего надеяться применить другое с тем же успехом.

Это и есть всесильный принцип дополнительности Бора, сформулированный им следующим образом (слово «классический» относится к традиционным законам старой устоявшейся физики): «Любое использование классических представлений немедленно приводит к отказу от использования других классических представлений, в разных аспектах одинаково необходимых для объяснения явления»[209].

Для того чтобы почувствовать, что такое принцип дополнительности, ниже предлагаются четыре коротких вымышленных примера.

ПЕРВЫЙ ПРИМЕР. Предположим, что вам дали игрушечный «атом», вылепленный из куска глины. Если бы вас попросили определить «длину» этого «атома», то вы могли бы скатать глину в «колбаску» полуметровой длины. Если бы вас спросили о диаметре «атома», вы могли бы подумать о шаре, затем скатать глину в шарик диаметром 5–6 см и измерить. Поступая подобным образом, вы не можете ответить сразу на оба вопроса. Эта выдумка показывает тот путь, по которому наш выбор вопроса контролирует способ ответа и который запрещает взаимоисключающие эксперименты. Эта иллюстрация, однако, вводит в заблуждение, так как глина остается у вас в руках и вам никто не запрещает пытаться выполнить оба задания с одной и той же глиной.

ВТОРОЙ ПРИМЕР. Предположим, что у вас в руках только что вылупившийся жук, последний из своей разновидности. Если необходимо узнать, как долго могут жить молодые жуки данной разновидности без пищи, можно поместить его в коробку и проверить, сколько он проживет. Если же нужно узнать, за какое время жук удваивает свой вес, находясь на сахарной диете, можно кормить его и наблюдать за его успехами. Однако нельзя проделать оба этих эксперимента с одним и тем же жуком. Оба эксперимента взаимно исключают друг друга. Эта выдумка показывает, как выбор одного вопроса полностью отрезает нам возможность ответить на другой. Данная иллюстрация, однако, также вводит в заблуждение, поскольку это такая ситуация, которая меняет наши планы (надежды), но не поведение природы: оба вопроса нормальны, и мы только искусственно создали видимость трудности.

ТРЕТИЙ ПРИМЕР. Некий нервный вкладчик, вложивший свои сбережения в банк, дрожит за свои деньги и желает убедиться, что они в целости и сохранности. Он пытается удостовериться в этом двумя способами.

а) следит за регулярностью выплаты интересующих его процентов и по ним заключает, что его деньги в банке;

б) ярко представляя себе, как в детстве заглядывал в свою свинку-копилку, иногда заходит в банк и просит показать ему его деньги. Банк соглашается на это, но предупреждает, что так дело дальше не пойдет. (Далее ему объясняют, что, если всем вкладчикам вздумается выдвигать подобные требования, банк вообще не сможет нормально работать.) Вкладчик с успехом может воспользоваться обоими способами. Однако каждый из этих способов заставляет его отказаться от другого, поскольку выглядит достаточно надежным. Вкладчику приходится изменить свое представление о банковском деле и зарубить себе на носу, что, хотя его деньги и в безопасности, это все же не то, что хранить их у себя в подвале.

ЧЕТВЕРТЫЙ ПРИМЕР. Предположим, имеется маленький ящик вроде спичечной коробки, из которого доносится какое-то поскрипывание. Двум лицам предлагается, не открывая ящик, исследовать, что там внутри. В — любитель-биолог слушает и решает, что внутри ящика сидит насекомое, скорее всего сверчок. Решив так, В может задаться рядом научных вопросов и ответить на них. Он вслушивается в звуки, определяет их тональность и длительность и, зная, что сверчок издает звуки, потирая ножки друг о друга, оценивает (можно себе вообразить) число зазубрин на ножках сверчка и расстояние между ними. Это даже может его навести на мысль о том, к какой разновидности сверчков следует отнести сидящего в ящике. Это хорошая догадка на основании его гипотезы — но в своем желании понять, что же внутри ящика, В может не заметить, какое ограничение он накладывает сам на себя своей первой гипотезой.

Между тем Е — радиоинженер — смотрит, слушает и решает, что внутри ящика помещен маленький транзисторный передатчик. По размеру ящика и высоте звука он прикидывает (можно себе представить) величину электрической емкости, которая дает такие поскрипывания.

Затем В и Е встречаются. Несмотря на коренное различие в объяснении, они соглашаются продолжить эксперимент. Им пока еще не позволяют открыть ящик, но разрешают в щелку капнуть немного машинного масла. Тон скрипа понижается. Биолог В говорит: «Это как раз то, что я предполагал — в вязком масле сверчку тяжелее двигать ногами». Инженер Е говорит: «Это разрешает все сомнения — масло, попадая между обкладками конденсатора, всегда увеличивает его емкость, что и должно приводить к понижению высоты звука». Каждый полагает, что эксперимент свидетельствует в пользу его объяснения, но при этом он забывает, что проделанный им опыт получает смысл только в рамках выбранного им самим способа объяснения.

Дополнительность

Дополнительность имеет место во многих областях интеллектуальной деятельности человека: в науке, философии, этике, наконец, в самой жизни. Существует много вещей, обладающих различными, взаимоисключающими друг друга свойствами. На основании опыта, приобретенного в атомной физике, нельзя утверждать: «это противоречащие друг другу точки зрения». Досадно, что каждое кажется верным, и раздражает, что одна точка зрения полностью отрезает нас от других. Однако тут следует винить доставшуюся нам в наследство от древних греков способность мыслить с помощью категоричных да и нет. Следует уразуметь, что наше неудовольствие происходит от необходимости вести себя не способом А, не способом В, а неким неизвестным образом, скажем типа А, в случае чего необходимо забыть о способе В. Вместо этого следует научиться иметь в виду обе точки зрения, используя каждую наиболее рациональным образом.

На фиг. 211 изображена модель, служащая для демонстрации дополнительности[210].

Фиг. 211. «Игральный ящик» для иллюстрации дополнительности.

Две игральные кости помещены на концах длинного выдвижного ящика АВ в отделениях со стеклянными окошками. Выдвижной ящик вставляется в туннель так, что можно вытягивать его то с одного конца, то с другого и видеть кости. Чтобы посмотреть на кость А, нужно вытянуть ящик за конец А. При этом кость А видна, а В — нет. Чтобы посмотреть на кость В, нужно вдвинуть ящик в туннель настолько, чтобы показалась кость В. Движение ящика включает опрокидывающий механизм (расположенный в туннеле), который подбрасывает вторую кость, когда первая показывается из туннеля. (Это можно делать рукой, ударяя по резиновому дну ящика.) Механизм включается только тогда, когда ящик проходит больше половины пути через туннель. Так, если полностью вдвинуть ящик в туннель (обе кости внутри туннеля), а затем снова его вытянуть за тот же конец, то число очков на кости окажется тем же самым. Можно вытягивать ящик за конец А сколько угодно раз, но каждый раз будет видна одна и та же грань кости А. Если, однако, ящик вдвинуть поглубже, так чтобы показалась кость В, то можно услышать, как перед этим срабатывает подбрасывающий механизм. После этого уже нельзя с определенностью сказать, какое число очков покажет кость А, когда ее вытащат в следующий раз. Когда видишь, что выпало на одной кости, то не знаешь, что будет на другой.

Это не «модель» в научном понимании, а всего лишь механическая игрушка, демонстрирующая дополнительность. Если концу А сопоставить «положение электрона» (или «где?»), то конец В следует обозначить как «импульс» (или «как быстро?»). Но если концу А приписать «кинетическую энергию частицы», то концу В следует сопоставить «время». Существует много других пар величин, дополнительных — важных и взаимоисключающих друг друга. Если иметь дело с одной из них, то при этом полностью исключается знание другой. Ниже приведен список таких величин, составленный Уилером:

Дополнительность не противопоставляет противоположности, скажем любовь и ненависть, а только объединяет взаимоисключающие свойства одного и того же, такие, как любовь и правосудие. Следует научиться жить с учетом дополнительности.

ЕЩЕ НЕМНОГО ТЕОРИИ

Предсказание новой частицы. Мезон Юкавы

В качестве последнего примера физической теории предлагается проследить, как из корпускулярно-волновой теории вытекает необходимость существования неожиданной субатомной частицы — мезона, представляющего собой нечто среднее между электроном и протоном. (Нижеследующее представляет собой примитивное изложение громадного раздела чистой теории. Способ изложения выбран не наилучший и даже не совсем физический. Его следует скорее рассматривать в качестве наводящего. Вспомните, что зачастую верный подход обнаруживается при грубой попытке рассмотрения вопроса, подобно тому как это делается ниже.)

Тридцать лет назад, когда в рамках новой корпускулярно-волновой физики разрабатывалась структура атомов, структура ядер еще оставалась загадкой, частично разгаданной, а частично неясной, заставлявшей думать о существовании неких неизвестных сил, цементирующих ядро. В атомах электроны и ядра связаны электрическими силами, обратно пропорциональными квадрату расстояния, причем картина волн де-Бройля определяет вероятности их расположения. Внутри же ядра должны существовать другие силы, которые уравновешивают силы электрического отталкивания протонов и заставляют протоны и нейтроны находиться вместе. Действительно, из опытов по рассеянию следует, что такие силы существуют внутри ядра. Когда быстрые α-частицы или протоны налетают на ядра, часть из них при столкновении на близких расстояниях рассеивается назад на большие углы, причем число их оказывается неожиданным. Их оказывается гораздо меньше, чем можно было бы ожидать, если исходить из отталкивания по закону «обратного квадрата расстояния», т. е., видимо, должны действовать новые силы, силы притяжения, причем такие, действие которых ощущается только на очень малых расстояниях от ядра[211]. В модели «холма» потенциальной энергии такие «короткодействующие силы» заставляют кривые потенциальной энергии загибаться вниз и спускаться в кратер. На краю кратера короткодействующие силы притяжения уравновешивают силы электрического отталкивания, действующие на налетающую заряженную частицу. На внешнем склоне «холма» силы скоро обращаются в нуль, внутри же кратера они оказывают исключительно сильное влияние на любую частицу в ядре. Из экспериментов по облучению следует, что для ядер радиус кратера в среднем примерно составляет 1,4∙10^-15∙(А)^1/3 м, где А — атомный вес. Будем называть это расстояние радиусом ядра r. Следовательно, относительно радиуса действия ядерных сил нам уже что-то известно. По измеренным энергиям связи можно было бы оценить размеры ядра при плотной упаковке. Однако истинная природа или механизм их действия оставались неизвестными, и никто не представлял себе, как связать их с макромиром.

В 1935 г. японский физик Юкава выдвинул потрясающее предположение: внутри ядра всегда находятся некие субатомные частицы, которые испускаются одними нуклонами и поглощаются другими. О таком «процессе обмена» ранее никто не догадывался. Если бы подобные частицы обладали подходящей массой и в некоторых случаях зарядом, то обмен ими объяснял бы ядерные силы. (Это нечто вроде эффекта связи двух ненавидящих друг друга партнеров по теннису через теннисный мяч. Пока мяч носится по корту, партнеры остаются на теннисной площадке.) Картина таких «обменных сил», следует из теоретической схемы, построенной физиками-теоретиками для «объяснения» обычных электрических сил, таких, как силы электрического отталкивания двух электронов. Рассмотрим вначале эту схему.

Как электроны отталкивают друг друга? Можно говорить, что каждый из них действует на другой посредством электрического поля. Однако для объяснения связи, существующей между электрическим полем и электроном, в настоящее время в качестве необходимого компонента привлекают фотоны. Когда электрон, движущийся ускоренно, излучает (или поглощает) фотон, то между излучением и электроном происходит обмен энергией и импульсом, в результате чего электрон испытывает действие силы. Если же электрон двигался бы в поле электрических сил без ускорения, то физики-теоретики и в этом случае могли бы сказать, что происходит обмен энергией и импульсом через фотоны. Правда, такие «виртуальные» фотоны испускались бы и поглощались столь быстро, что их никогда не удалось бы увидеть. Такие фотоны, «отскакивая» от электрона (или какой-нибудь другой заряженной частицы), уносили бы с собой импульс и создавали бы силу. Тогда это были бы те наблюдаемые силы, которые действуют на заряд со стороны электрического поля. Иногда при ускорении электрона один из таких фотонов вырывается из «связки» и улетает в виде наблюдаемого кванта света. За исключением таких фотонов, виртуальные фотоны не наблюдаемы. Однако можно себе вообразить обмен такими фотонами электронов, когда один из них некоторую малую часть времени (по-видимому, около 1 %) проводит в состоянии с большей энергией, поглотив один из таких фотонов. (Если подобная картина для вас выглядит дикой и раздражающе непонятной, вспомните, что это лишь некая теоретическая модель для того, чтобы перенести на атомы наши привычные способы рассуждения. Ее использование плодотворно, она позволяет делать предсказания и расширяет круг наших представлений.)

Юкава пытался найти механизм, посредством которого протоны и нейтроны удерживаются в ядрах. Эти силы ведут себя различно на разных расстояниях: с увеличением расстояния они уменьшаются от громадных значений внутри ядра до пренебрежимо малых значений сразу вне «кратера», причем гораздо быстрее, чем по закону 1/r². Юкава убедился, что частицы с нулевой массой покоя, такие, как фотон, не могли бы играть роль связующего агента для таких сил. Чтобы объяснить известные об этих силах экспериментальные сведения, необходимо было приписать частицам некоторую массу покоя. Такие частицы могли бы обеспечить ядерные силы, рождаясь, переходя к другому нуклону и поглощаясь им прежде, чем самый искусный экспериментатор успевал бы заметить какие-либо изменения энергии. Попытаемся здесь дать оценку массы такой частицы. (Опираясь на твердо установленный в настоящее время факт, что такие частицы действительно существуют, будем использовать для этой частицы ее современное название — «мезон».)

Представим себе, что возникший мезон перед тем, как поглотиться, успевает в течение короткого времени совершить несколько оборотов над краем ядерной ямы — подобно электрону на боровской орбите, но с гораздо меньшими размерами. (Ниже будут рассмотрены другие предположения о волновом поведении мезона.) Для существования такой «орбиты» волна де-Бройля должна представлять собой стоячую волну в форме окружности радиусом r, причем в простейшем случае на длине этой окружности 2πr должна укладываться одна длина волны λ. Тогда

λ = 2π∙r

Поскольку для любой частицы λ = h/mv, то отсюда mv = h/2π∙r.

Выше только говорилось о частице (не заботясь о деталях), масса же ее m и скорость v остаются неизвестными. Если сказать, что v равно с, то ясно, что это будет переоценка (если, конечно, только частица не является фотоном, масса покоя которого равна нулю, а скорость точно равна с). Если же сказать, что m равна массе покоя мезона m₀, то это будет недооценкой. Для грубой прикидки скомбинируем оба эти приближения, надеясь, что при этом неточности скомпенсируются: напишем m₀с вместо mv и получим

m₀с = h/2π∙r

Отсюда m₀  = h/2π∙r∙c, и величину m₀ можно оценить по известным значениям h, с и оценке радиуса ядра r ~= 1,4∙10^-15 м:

m₀  = (6,62∙10^-34 дж∙сек)/(2∙3,14∙(3,0∙10⁸ м/сек)∙(1,4∙10^-15 м)) ~= 250∙10^-30 кг

Сравните это значение с массой покоя электрона, равной примерно 0,9∙10^-30 кг. Чтобы успеть просуществовать (недолго) в ядре и обеспечить соответствующие силы связи на соответствующих расстояниях, «обменная» частица должна обладать массой покоя в несколько сот электронных масс. Это означает, что она должна быть в 5 или 10 раз легче, чем самый легкий атом.

Вскоре после этого предсказания, казавшегося столь странным и фантастическим, промежуточные частицы были обнаружены среди треков, оставленных космическими лучами в камере Вильсона. Вначале это выглядело как поразительное подтверждение предсказания — даже величина массы была примерно правильной. Затем оказалось, что у новых частиц, явно нестабильных, время полураспада и другие характеристики не согласовывались с предсказаниями теории. Однако последующие экспериментальные поиски привели к обнаружению еще большего числа разных частиц. Некоторые из них оказались такими, какими их предсказал Юкава, и, как теперь думают, играют в ядрах роль необходимого связующего материала. В настоящее время для дальнейшего изучения можно создавать на ускорителях самые разнообразные мезоны, причем свободные, вне ядер.

Мезоны как вполне реальные частицы в настоящее время стали привычным понятием в субатомной физике. Мезонная теория играет важную роль в ядерной физике. Измерения мезонных масс (~270 электронных масс)[212] подтвердили гипотезу Юкавы, высказанную тогда, когда таких частиц никто не наблюдал и о существовании которых никто не догадывался.

[Замечания по поводу других моделей волнового поведения мезона в ядре:

1) Картина стоячей кольцевой волны выглядит слишком надуманной. С физической точки зрения лучше представлять себе мезон блуждающим внутри кратера потенциальной ядерной ямы. В этом случае представление о стоячей волне де-Бройля было бы более похожим на задачу о колеблющейся струне. При этом предположении простейшая стоячая волна должна иметь нулевую амплитуду на краях ямы (здесь располагаются узлы волны). При этом ¹/₂ λ равна диаметру ядерного кратера, равному 2r, или λ = 4r вместо λ = 2π∙r.

2) При более последовательном рассмотрении нет необходимости привлекать ни волны, ни яму, а следует исходить из принципа неопределенности в том его виде, в котором он формулируется для энергии и времени:

ΔE∙Δt = h/2π (по крайней мере)

Пусть один нуклон в ядре испускает мезон и передает его какому-нибудь другому нуклону, отстоящему от первого на расстояние где-то между 0 и 2r. Изменение энергии ΔE, т. е. ее неопределенность в данный момент времени, равна энергии, затраченной на образование мезона, т. е. m₀с². Предположим, что свой путь до другого нуклона, в среднем равный r, мезон проходит со скоростью с. На это уходит время, равное Δt = r/c. Если мезон живет достаточно долго, успевая пройти этот путь и оставаясь незамеченным экспериментатором, то ΔE∙Δt должно в точности равняться h/2π, и, следовательно,

(m₀с²)∙r/c = h/2π

Отсюда следует ранее найденная оценка массы мезона m₀ = h/2π∙r∙c]

ЕЩЕ ОДИН ЭКСПЕРИМЕНТ

Видимые атомы

Для того чтобы ознакомиться с последним в этой главе разделом экспериментальной физики, оставим фантазирование и посмотрим на фотоснимки отдельных атомов, хитроумные способы получения которых теперь можно обсудить с техническими подробностями. На фиг. 215 изображена фотография атомов, расположенных на самом острие вольфрамовой иглы. Изображение создается ионами гелия, рассеянными острием иглы, на флуоресцирующем экране. На фиг. 212 показана установка, сконструированная Эрвином Мюллером[213].

Фиг. 212. Ионный микроскоп Мюллера для наблюдения атомов.

_{На рисунках даны простейший вид прибора и пояснения принципа его действия. Для более подробного ознакомления см. Scientific American, 196, June 1957.}

Очень острая вольфрамовая игла помещается в центре стеклянной колбы, внутри которой имеется хороший вакуум при незначительном содержании газа гелия. Между нитью и опоясывающим ее металлическим кольцом радиусом r прикладывается высокая разность потенциалов. Так как игла очень острая, электрическое поле вблизи ее острого конца исключительно велико. Оно настолько велико, что способно у атома гелия, проходящего мимо острия иглы, вырвать электрон[214]. Образовавшийся ион ускоряется электрическим полем. Он летит от поверхности по прямой и падает на круглый экран, покрытый флуоресцирующей краской, заставляя экран светиться при ударе. (Падающий на экран ион выбивает в краске электроны, а когда атомы вещества краски обретают их снова, то они высвечиваются.) Электрическое поле вблизи острия иглы особенно велико, причем силовые линии поля выходят из поверхности (в той степени, в какой о поверхности можно говорить в атомном масштабе) в перпендикулярном к ней направлении. Поэтому ионы ускоряются этим полем в направлении, перпендикулярном поверхности. На некотором отдалении от острия, там, где поле слабее, скорость и направление движения ионов уже меняются слабо. Поэтому вспышки на экране от ударов ионов в точности воспроизводят увеличенную картину расположения точек, с которых они стартовали на поверхности острия. Там, где на поверхности иглы имеются заострения, электрическое поле у поверхности ее очень сильное и способно создавать и ускорять большую часть ионов гелия. Следовательно, яркое пятно на экране соответствует заострениям или ребрам на поверхности иглы.

Теперь вообразим себе иглу в атомном масштабе. Ее «конец» представляет собой последний слой атомов вольфрама, который лежит на чуточку более широком слое атомов, а тот в свою очередь лежит на еще более широком слое и т. д. Острие может быть столь острым, что последний слой состоит всего лишь из десятка атомов или несколько большего числа их. Однако даже в этом случае атомам гелия конец иглы не представляется очень острым. Что уж действительно выглядит острым, так это края слоев атомов, те места, где какой-нибудь слой обрывается и «поверхность» образует ступеньку между поверхностями соседних слоев.

Картина дифракции рентгеновских лучей говорит о том, что металлический вольфрам кристаллизуется в виде регулярной последовательности атомных слоев, напоминающей аккуратно сложенную горку апельсинов или древних пушечных ядер. На фиг. 213, а изображена модель такой упорядоченной горки, сделанная из маленьких пробковых шариков. Точно так же, как на конце острия иглы, в этой горке у каждого слоя имеются боковые грани, причем каждый следующий слой на несколько шариков шире. Пометив крайние шарики каждого слоя, можно предсказать, какое изображение будет давать острие настоящей иглы из вольфрама. Все крайние шарики на модели были закрашены флуоресцирующей краской, светящейся в ультрафиолетовом свете. На фиг. 213, б приведена фотография этой модели, сделанная в ультрафиолетовом свете. Сравнивая ее с фиг. 213, в, сделанной с помощью настоящей установки, можно убедиться, что картина, создаваемая пучком атомов гелия, отражает подлинную картину послойного расположения атомов вольфрама.

Такие эксперименты должны выполняться при очень низких температурах, иначе собственное движение атомов гелия будет вносить заметные искажения, — желательно, чтобы ионы двигались только за счет электрического поля. Кроме того, при обычных температурах атомы гелия, по-видимому, рассеиваются на атомах вольфрама без последующей ионизации: для ионизации, вероятно, необходимо их более длительное пребывание в электрическом поле, а это имеет место лишь тогда, когда ионы движутся медленно.

Фиг. 213. Интерпретация изображения острия иглы в ионном микроскопе. (Из Scientific American, 196, June 1957.)

_{а — модель из уложенных слоями пробковых шариков для воспроизведения картины расположения атомных слоев на конце очень острой вольфрамовой иглы; б — крайние шарики каждого слоя модели а были покрашены флуоресцирующим веществом, способным светиться в ультрафиолетовом свете; здесь приведена фотография этой модели в ультрафиолетовом свете; в — фотография, сделанная с помощью ионного микроскопа. Изображение создается ионами, летящими с острия вольфрамовой иглы.} 

Фиг. 214. Вид острия вольфрамовой иглы (помещаемой в ионный микроскоп) и обычной острой иглы (слева) в обычном оптическом микроскопе.

_{Фотография Эрвина В. Мюллера.}

Поэтому аппаратура охлаждается жидким водородом (спокойно кипящим в сосуде с кипящим азотом). При этом изображение таково, как на фиг. 215.

Фиг. 215. Фотография острия вольфрамовой иглы, сделанная на ионном микроскопе.

_{Фотография передает картину расположения атомных слоев на кончике иглы и ее боковых сторонах (увеличение 3 000 000). (Фотография Эрвина В. Мюллера, Пенсильванский университет.)}

Если дать вольфраму чуть-чуть нагреться, то картина еще остается прежней, но при этом видно движение некоторых атомов вольфрама: видно, как некоторые из них мигрируют и испаряются.

Правильно ли сказать: «На этой фотографии я вижу сами атомы непосредственно»? Это зависит от уровня вашего мышления. Если вы не знаете, что такое электрическое поле, что такое распределение заряда и поля вблизи острия, что такое ионизация, средняя длина свободного пробега, свечение экрана… вы, наверное, скажете: «Какое там непосредственно! Эта картина — всего лишь какая-то система пятен плюс туманные рассуждения насчет атомов».

Однако, будучи уже знакомым с достижениями науки, вы можете с уверенностью воскликнуть: «Да, я вижу сами атомы!» И за этим утверждением будет скрываться обретенное вами глубокое понимание.

ЛЮДИ НАУКИ

Ученые

Я надеюсь, что здесь, в конце курса, вы поразмышляете об ученых и о том, ради чего они делают открытия и объясняют их. Пифагор… Птолемей… Коперник… Тихо… Кеплер… Галилей… Ньютон… Джоуль… Максвелл… Резерфорд… Эйнштейн… де-Бройль… Бор — все они сделали великие открытия, все внесли вклад скорее в наше интеллектуальное богатство, чем в житейские блага или успехи, и то, что они дали нам, составляет непреходящие ценности, достающиеся бесчисленным поколениям. При взгляде в будущее мы видим обширную область фактов, законов, теорий, предположений — научные знания, — которая будет увеличиваться все больше и, как мы надеемся, будет стремиться к завершенности. Это изучение природы — составляющая часть интеллектуальной жизни человека — приносит удовлетворение всем ученым. Наука в их руках — это не только деятельность по собиранию фактов, или установлению законов, или выбору направления экспериментов. Это прежде всего искусство чувствовать, как лучше выбрать точку зрения или наиболее подходящее направление исследований, чтобы расширить понимание природы. Чистая наука — погоня за знаниями и пониманием природы — всегда будет удовольствием. Что же, ученые в их башне из слоновой кости, башне из экспериментов и теорий работают лишь для себя, ничего не давая остальному человечеству, подобно безмолвным поэтам в уединении? Ответ мыслителя: «Нет, они прибавляют человеку интеллектуальные возможности». Ответ практика: «Нет, ученые полезны, поскольку со временем их открытия используются в технике». Но сегодня существует новая группа исследователей-инженеров, которые соединяют деятельность ученого и инженера, и наш вопрос становится более общим. В каком вообще соотношении по их значению для человечества находятся ученые, инженеры и инженеры-физики?

Ученые и инженеры

Наука дает технике возможность развиваться и процветать. Современный инженер[215], используя научные знания, выполняет великолепную работу и всюду необходим. Лет сто назад хороший инженер опирался главным образом на огромные запасы опыта эмпирического экспериментирования и изучения методом проб и ошибок, унаследованного от предыдущих поколений. Но теперь, когда потребности и методы усложнились и меняются более быстро, хорошие инженеры опираются непосредственно на научные знания. Это изменение состоит в современной технике в уменьшении «степени эмпиризма», как ее назвал Джеймс Б. Конант[216]. Для инженеров это означает продвижение вперед, но оно делает их более зависимыми от помощи ученых. Они теперь используют так много научных материалов, сконцентрированных в компактные формулы или таблицы в справочниках, что остается слишком мало времени для изучения их источников; поэтому им приходится либо принимать эти материалы на веру, либо консультироваться у научных советников.

Современный инженер-физик — творческий инженер или ученый-прикладник — объединяет в себе инженерное искусство с основательными знаниями науки. Он обладает творческими способностями и вооружен научными знаниями вплоть до последних достижений. По своей подготовке и роду занятий он — ученый, но его интересуют больше новые применения науки, чем сами новые достижения науки. Таким образом, инженер-физик занимается интерполяцией в той или иной области существующей науки, тогда как чистый ученый по своему призванию стремится к достижению новых знаний и более глубокого понимания и, стало быть, пытается провести экстраполяцию. С учетом этого отличия цивилизация должна была бы оценивать чистых ученых наравне с поэтами и артистами. Все ученые так или иначе вносят вклад в интеллектуальное и эмоциональное развитие человека.

Однако у практика остаются вопросы: «Инженер-физик использует все науки как зерно для своей мельницы, и он энергично работает над развитием самой науки. Почему же тогда при наличии многих лучших умов, занимающихся технической физикой, необходимы чистые ученые?» Я думаю, на это существует ответ: «Ученый в своей башне из слоновой кости вносит такой вклад, без которого не может обойтись в течение длительного времени ни нация, ни цивилизация: он обеспечивает интеллектуальной пищей следующее поколение ученых и инженеров. Техническая физика, подобно мулу, обладает силой и умом, но не может воспроизвести подобное себе следующее поколение. Причина в том, что

следующему поколению первоклассных инженеров-физиков необходимы свежие взгляды и знания и новая мудрость, если они хотят работать как творцы, а не как обычные технические руководители. И эти свежие взгляды появляются из философских интересов, которые поддерживают и развивают ученые». Чистый ученый обязательно в какой-то мере философ; он размышляет над своими собственными мыслями, критически рассматривает свои собственные эксперименты и приобретает общий взгляд на свою науку. Он знает кое-что о том, на чем основаны его знания; он немного знает о том, что он знает, и он всегда ясно может сказать, чего он не знает. И в возрастании своего знания он находит глубокое удовлетворение.

Квалифицированный ученый

Что делает ученого специалистом по сравнению с непрофессионалом? Каждый из нас является непрофессионалом, любителем и дилетантом во всех областях, за исключением нашей собственной. Мы в состоянии изучить правила и использовать их, забывая о том, что мы не профессионалы, но мы делаем с ними серьезные ошибки. Неученый может купить маленькую книгу, в которой сообщаются «все законы физики», — он может даже пересчитать наиболее важные из них на пальцах двух рук. Профессиональный физик знает законов не больше — он может помнить даже меньшее число законов, поскольку он полагается на книги, которые напомнят то, что потребуется ему, но он держит в уме два обширных комментария к фактам, законам, принципам… два комментария, которые являются продуктом его образования, опыта и размышлений.

1. Он знает ограниченность каждого факта или закона, пределы его применимости, смысл его терминов, он имеет широкие представления о его связях с реальным материалом. Такие знания образуют то, что мы называем «маленькой черной записной книжкой в кармане ученого», — символ богатого опыта, имеющегося у ученого и отличающего его от осведомленного непрофессионала, который может цитировать законы, но не умеет надежно их использовать. (Он знает, например, что в некоторой формуле изгиба балки Р — это напряжение, а не сила, что формула применима лишь при малых растяжениях и много больших сжатиях. Он никогда не спутает Р с силой и не применит формулу к дереву, которое изгибается и раскалывается совершенно иначе. Аналогично он знает, почему закон Бойля применим для газов при очень низких давлениях, поэтому он не будет ожидать, что этот закон останется справедливым также при очень низких температурах.) Эту записную книжку можно назвать «детальные знания и понимание».

2. Далее мы видим, что каждый хороший ученый имеет другую «записную книжку», которая сообщает ему, каким образом взаимосвязаны его конкретные знания. Ее объем очень велик, неограничен. Ее можно назвать «теория».

Обладание этими двумя воображаемыми записными книжками достигается в процессе обучения, что делает ученого специалистом. Как образованный неспециалист вы можете идти дальше вперед, чтобы присоединиться к ученым, если вы понимаете, как он пользуется этими «записными книжками».

Гений и чудак

Каждому из нас — будь то ученый, инженер или неспециалист — доводилось встречать энтузиастов, предлагающих новые научные взгляды — не изобретения или хитроумные приспособления, а революционизирующую теорию. Как отличить блестящее достижение от нелепого вздора? Все можно нарядить так, чтобы это выглядело привлекательным и разумным для постороннего человека. Больше того, все может выглядеть обещающим успех и вполне возможным даже в глазах специалиста. Мы все делаем ошибки при распознавании «чудаков»: мы смеемся над непризнанными гениями или преклоняемся перед бессмыслицей, облеченной в звонкие фразы; но ученый, с его развитым чутьем к своему искусству, имеет наилучшие шансы отличить пророка от чудака. Мудрость ученого основана на прошлых знаниях, но сам он глядит в будущее. Инженеру-физику, смотрящему главным образом в настоящее и прошлое, труднее отличить пророка от чудака.

Чудак — это зачастую искренний ученый по своим намерениям, а временами и по образованию, который стремится к новым взглядам, что уводит его от последовательного познания природы. В его смелых размышлениях и мыслях нет вреда — они свойственны и хорошей науке, — опасна его некритическая уверенность в своей правоте. Если ученый экстраполирует, а инженер интерполирует, то чудак предполагает и верит эмоционально, с закрытыми глазами. Весьма курьезно, но энтузиазм чудака заражает многих неспециалистов тем же самым слепым доверием. Мы надеемся, что, хотя эта книга и не сделает вас специалистом, ваши глаза будут открыты.

Удивление и восхищение. Интеллектуальный прогресс

Вместо сильного эмоционального убеждения, что его взгляды на природу — это истина в последней инстанции, для ученого главное чувство состоит в наслаждении поисками и достижением более широкого понимания природы. Его главная забота — рост знаний, а не их хранение. Он разделяет с нашими древними предками ощущение любопытства и чувство удивления и восхищения; он расширяет их до огромного чувства интеллектуального прогресса. У вас есть возможность разделить с ним это чувство.

Вы и Наука

Итак, наше рассмотрение физики в этом курсе прошло полный цикл, вернувшись к исходным вопросам о причинах, объяснениях, об эксперименте и теории. Вы не получите четкого заключения, говорящего, что следует называть «правильной» наукой; по существу, вам преподнесли еще более неоконченное, чем вначале, обсуждение этого вопроса; осталось еще больше знаний, требующих развития. Но сжатое воспоминание об упорядоченных фактах должно теперь выглядеть менее важным, чем чувство, что вы понимаете ученых и их работу, или чем убеждение, что наука имеет смысл как часть мудрости человечества.

Если вам доставляет удовольствие наблюдать за научными поисками, а у вас в душе остались некоторые вопросы для дальнейших размышлений; если вы получаете удовольствие от встреч, споров и работы с учеными; если вам нравится экспериментировать; если вы можете отличить «отважный консерватизм» теоретика от безбрежного энтузиазма «чудака», а прежде всего, если вы будете больше иногда читать о науке для себя как образованного человека, живущего в век науки, — тогда этот курс сделал свое дело.

Будущее науки — и практических знаний, и интеллектуального богатства — сильно зависит от отношения неспециалистов: родителей, учителей, должностных лиц, членов правительству… всех образованных людей; поэтому поддерживать доброе имя науки — дело рук каждого из вас как членов научной цивилизации.