Глава 21. Движение по окружности

We use cookies. Read the Privacy and Cookie Policy

«…все науки по мере совершенствования становятся по своему характеру математическими».

А. Н. Уайтхед (1911 г.)

Орбитальное движение

Что заставляет планеты двигаться по орбитам Кеплера? Почему они находятся в постоянном движении и почему их орбиты представляют собой эллипсы? Эти вопросы вытекают естественным образом из открытий Кеплера, согласно идущей еще от философов Греции древней традиции задавать вопрос почему. Астрономы измерили и зарегистрировали то, как планеты ведут себя, т. е. их видимые движения. Коперник и Кеплер показали, каким образом движение планет может быть описано простой схемой, но на все эти «почему» они отвечали лишь в духе своего времени. Коперник допускал существование вращающихся сфер, считая, однако, что их движение должно быть проще, чем это следовало из системы Птолемея; Кеплер представлял себе некие рычаги, осуществляющие воздействие Солнца на планеты и толкающих их вдоль направления их движения; он говорил о мистическом магнетизме, придающем форму орбитам. Его рычаги были реальны только в одном смысле: они были необходимы для выражения его второго закона и дошли до нас в образе геометрических линий, прочерчивающих площади.

Задача 1. Вычитание векторов

При изучении движения планет нам будет необходимо производить вычитание векторов. Эта задача дается вам для практики.

1. Обычное (арифметическое) вычитание. Предположим, что мы хотим из 5 вычесть 2. Это можно сделать различными способами:

а) можно сказать; 2, вычтенное из 5, дает 3, или то же самое, но другими словами: 5–2 равно 3;

б) можно изменить знак с + 2 на —2 и задать дополнительный вопрос: сколько будет 5 + (—2)?;

в) можно подойти к задаче по-детски и спросить: сколько мы должны добавить к 2, чтобы получилось 5?

Последний прием дает ключ к вычитанию векторов (или нахождению разности двух векторов).

2. Векторы. Предположим, что мы имеем «старый» и «новый» векторы и хотим найти их разность. Мы опрашиваем. «.Какой вектор нужно добавить к «старому», чтобы получить новый» вектор?» [Эта задача подобна вопросу пункта (в), однако теперь требуется выполнить геометрическое сложение.]

а) Если оба вектора, старый вектор 2 и новый вектор 5, направлены на восток, то какова будет их разность? Какой вектор нужно добавить к вектору 2, чтобы получился вектор 5? Изобразите это:

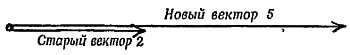
б) Если векторы (старый вектор А и новый вектор В) направлены в разные стороны так, как это показано на схеме

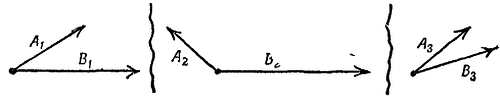
то что же тогда будет их разностью? «Что должно быть добавлено к вектору А, чтобы получился вектор В?» Покажите это стрелками для каждого случая. В каждом случае мы должны вычесть А из В.

в) Если векторы не приложены к одной и той же точке, вы должны сначала перенести один из векторов или оба в общую точку. После этого найдите, вновь пользуясь стрелками, разность В — А для каждого случая, изображенного здесь.

Кеплеровы жесткие «рычаги», предназначенные для осуществления движения планет, вскоре оказались ненужны: новое учение Галилея представило всю проблему в другом свете. По мнению Галилея, движущееся тело, предоставленное самому себе, будет продолжать двигаться; он предложил остроумный мысленный эксперимент для обоснования такого взгляда. Поколением позже Ньютон выразил то же самое посредством некоторого рабочего правила, а именно своего первого закона:

Каждое тело остается, в состоянии покоя или прямолинейного движения с постоянной скоростью, если на него не действует сила.

Позже Ньютон более четко представил эту расплывчатую идею о движении с помощью определенного количества движения, которое можно рассчитать путем умножения массы на скорость, и сформулировал второй закон:

Действующая сила изменяет количество движения в направлении своего действия.

СКОРОСТЬ ИЗМЕНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ ПРЯМО ПРОПОРЦИОНАЛЬНА ДЕЙСТВУЮЩЕЙ СИЛЕ.

Это было эквивалентно следующему утверждению:

Произведение массы на ускорение пропорционально результирующей силе.

В период между Галилеем и Ньютоном эти новые представления о движении (к которым на ощупь шли философы далекого прошлого и которые были частично установлены Леонардо да Винчи много раньше Галилея и Декартом после него) зрели для того, чтобы сыграть свою роль в астрономии. Члены только что созданного Королевского общества, которые вскоре приветствовали пришедшего в их ряды Ньютона, горячо обсуждали законы Кеплера, задавая совершенно другие вопросы почему. Они больше не беспокоились о внешнем воздействии, направляющем планеты вдоль их траекторий. Галилей убедил их, что нет никакой необходимости в подталкивающей силе; планеты будут продолжать двигаться сами по себе, если их оставить в покое, подобно куску льда на поверхности замерзшего пруда или пуле в пространстве.

Ученые отбросили представление о кеплеровых рычагах. Вместо них были введены внутренние силы, заставляющие планеты двигаться по искривленным орбитам. Такие силы создают усилие «поперек движения» планеты и будут сообщать ей импульс в новом направлении. Что это за силы? Новый вопрос повис в воздухе.

Гук, Гюйгенс и Ньютон взялись за его решение.

Считая орбиты планет примерно круговыми и опираясь на третий закон Кеплера, они предположили, что между Солнцем и планетами существует взаимное притяжение, которое уменьшается обратно пропорционально квадрату расстояния между ними (см. следующую главу). Но может ли эта сомнительная и совершенно непонятная сила заставить планеты следовать по эллиптическим орбитам в соответствии с первым и вторым законами Кеплера?

Разобраться в этом было непосильной задачей для всех, кроме Ньютона.

Задача потребовала ясной формулировки законов движения и искусного математического аппарата. Ньютон не только решил эту задачу, но и превратил это решение в основу хорошей теории.

Прежде чем изучать его работы, следует распространить обсуждение вопроса о силе и движении на случай новых сил, искривляющих траекторию движущихся тел. Вы уже встречались с аналогичной ситуацией при рассмотрении полета снарядов, когда вследствие силы тяжести к горизонтальному движению добавляется вертикальная составляющая и в результате траектория становится криволинейной. Это ускоренное движение кажется более легким для понимания. Осмелимся сказать: «кажется более естественным», нежели равномерное движение по круговой орбите с постоянной скоростью.

Фиг. 100.

Ускорение тела, движущегося по окружности

Рассмотрим планету, движущуюся по окружности (камень на веревке, или самолет, или атом, фиг. 101). Будут ли они иметь ускорение? Если нет, то нам трудно будет отыскать действующую на них результирующую силу, но тогда почему они не движутся вперед по прямой? Так все же не имеет ли планета ускорения' Конечно, ускорение вдоль направления ее движения отсутствует, ведь мы выбрали случай движения с постоянной скоростью. Может быть, имеется ускорение, направленное поперек движения планеты, перпендикулярно ему?

Попытаемся нарисовать векторы, с помощью которых можно было бы рассмотреть изменение (вектора) скорости. Пусть тело Р перемещается по окружности радиусом R с постоянной скоростью v, представляющей абсолютную величину вектора скорости тела Р. Направление скорости совпадает с направлением перемещения тела в каждый момент времени. В точке А вектор скорости тела v направлен, как это показано на фиг. 102, по касательной. Если тело движется с постоянной скоростью, то в точках А и В величина вектора скорости v будет одной и той же, но направление будет различным, оба вектора не идентичны. Между точками А и В происходит изменение скорости. (А вследствие этого и ускорение, а поэтому… продолжая эти рассуждения, мы доберемся до планетной астрономии.) Для определения «ускорения» рассчитаем изменение скорости и поделим его на соответствующий интервал времени. Такая процедура предусматривает вычитание векторов для нахождения изменения скорости, что уже было сделано в задаче 1 в начале этой главы.

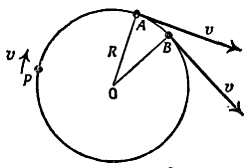
Фиг. 102. Векторы скорости.

Вывод формулы а = v2/R.

По мере движения тело Р изменяет свою скорость от (v вдоль АТ) до (v вдоль BT'). Для определения изменения скорости построим векторную диаграмму. Перенесем эти два вектора в общую точку X и проведем линию XY, представляющую вектор скорости v в точке А, и линию XZ, представляющую вектор скорости v в точке В.

Тогда XY будет «старая скорость», a XZ — «новая скорость». Каково же изменение скорости? Какой вектор следует добавить к старому вектору скорости для получения нового вектора скорости?

Такое изменение показано с помощью отрезка YZ, представляющего собой вектор и обозначенного Δv на фиг. 103.

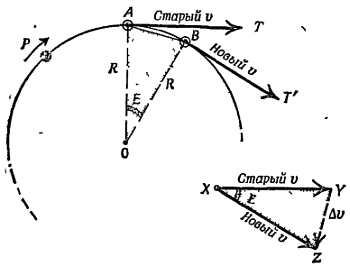
Фиг. 103. Изменение скорости.

Скорости направлены по касательным, перпендикулярным радиусам, поэтому треугольник ОАВ подобен угольнику XYZ векторной диаграммы

Тогда (Старый вектор v) + Δv путем сложения векторов дает (Новый вектор v).

Чтобы увидеть, куда направлен вектор Δv, изобразим заново первоначальный рисунок, но таким образом, чтобы векторы v сместились вдоль своих направлений до совмещения их точек приложения в точке С (фиг. 104).

Фиг. 104. Направление изменения скорости.

Тогда мы можем рассматривать точку С в качестве X, провести из этой точки старый вектор v и новый вектор v и провести также вектор Δv. Вектор Δv параллелен линии СО, проведенной из точки С в центр круга О. Если поместить точку В очень близко к А, то Δv будет направлен по радиусу от АВ к центру. Вектор Δv — это вектор скорости, направленный к центру круга.

Ускорение возникает только при изменении скорости[79]. Рассчитаем это ускорение путем деления величины изменения скорости Δv на интервал времени Δt, за который это изменение происходит. Время Δt равно времени прохождения телом Р расстояния по орбите между точками А и В со скоростью v. Фактически скорость v есть дуга 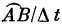. Для выражения Δv/Δt через v и R и т. д. мы вынуждены обратиться к геометрии, открытой современниками Ньютона. Соединим А и В хордой А‾В‾. Вся хитрость состоит (как это часто делается для решения геометрических задач) в добавлении одной вспомогательной линии, в данном случае хорды А‾В‾.

Рассмотрим теперь подобные треугольники на реальном рисунке и векторной диаграмме скоростей (фиг. 103). Радиусы ОА и ОВ на реальном рисунке образуют небольшой угол Е. Векторы скорости направлены по касательным перпендикулярно радиусам так, что вектор старой скорости v и вектор новой скорости v образуют тот же маленький угол Е[80]. Тогда на реальной картинке мы имеем треугольник ОАВ с равными сторонами R и R, образующими угол Е; на векторной диаграмме имеется треугольник XYZ с равными сторонами v и v, образующими тот же угол Е. Поэтому треугольники ОАВ и XYZ подобны. Значит, должно иметь место следующее соотношение:

(Короткая сторона, Δv / Одна из равных сторон, v) = (Короткая сторона, АВ / Одна из равных сторон, R)

в некотором треугольнике Δv/v = A‾B‾/R… в реальном треугольнике Δv = v∙A‾B‾/R

Теперь мы можем рассчитать «ускорение»:

УСКОРЕНИЕ = Δv/Δt = (v∙A‾B‾/R)/Δt = (v/R)∙(A‾B‾/Δt)

Для дальнейшего нам необходимо установить, что такое A‾B‾/Δt.

Что представляет собой [(хорда A‾B‾), деленная на (время движения от А до B)]? Мы знаем, что такое дуга 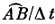. Это отношение (расстояние)/(время) на участке орбиты от А до B, т. е. скорость v. Но для очень короткой дуги, когда В близко к А, криволинейная дуга  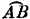очень близка к хорде A‾B‾.

Посмотрите на серию картинок, показанных на фиг. 105.

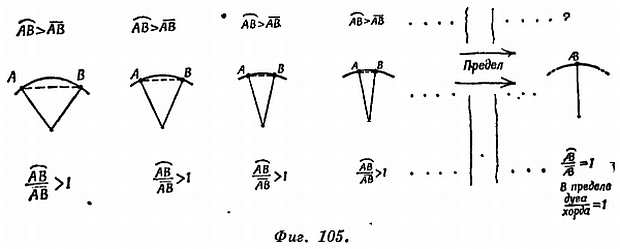
По мере сближения А и В дуга 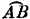и хорда A‾B‾ становятся все меньше, в то же время уменьшается и различие между ними[81]. Говоря математическим языком, мы приближаемся к «пределу», когда В совпадает с А. Мы никогда не достигаем этого предела, но мы можем к нему приблизиться настолько, насколько захотим, и сделать различие между дугой и хордой настолько малым, насколько захотим.

Однако мы не только можем сделать разность 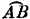 — A‾B‾ пренебрежимо малой — мы можем сделать пренебрежимо малым отношение (разность/хорда) или ( 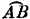— A‾B‾)/A‾B‾. Это приводит к тому, что 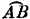/A‾B‾ становится очень близким к единице. Таким образом, мы можем сказать, что при большом расстоянии между А и В дуга немного больше хорды, при малом расстоянии дуга примерно равна хорде, а при еще меньшем расстоянии дуга почти равна хорде. При сколь угодно малом расстоянии в пределе дуга равна хорде. Математики предпочитают описывать этот предел так: LIm(дуга/хорда) = 1. Теперь мы хотим определить ускорение в некоторый момент времени, когда В и А практически совпадают. Мы не собираемся определять значение этой величины, усредненное по большому расстоянию. Мы хотим знать предел ускорения, когда В совпадает с А. Таким образом, мы говорим: дуга = хорда,  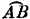— A‾B‾. Тогда

Дуга/Δt = Хорда/Δt, или 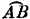/Δt = A‾B‾/Δt в пределе.

Следовательно,

Ускорение = Δv/Δt = (v/R)∙A‾B‾/Δt = (v/R)∙(v), в пределе (v/R)∙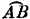/Δt

так как 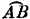/Δt есть v. Тогда ускорение Δv/Δt = (v/R)∙(v) или v2/R

или (Скорость на орбите)2/(Радиус орбиты)

Это соотношение ускорение — v2/R очень важно. Мы будем использовать его в теории движения планет, при изучении движения электронов, при изготовлении масс-спектрографов и конструировании циклотронов — везде, где мы сталкиваемся с движением по орбите. Было бы очень важно повторить для себя вывод этого соотношения и поверить в его значение. Поняв, как это делается, вы можете сократить вывод, ограничившись коротким объяснением, двумя эскизами и несколькими алгебраическими выражениями.

Два важных вопроса

Полученный нами результат, ускорение = v2/R, вызывает два вопроса:

1. Каким образом может движущееся тело иметь ускорение, но не двигаться быстрее или же не перемещаться к центру круга?

2. Не нужна ли сила для ускорения тела в направлении его движения в соответствии с соотношением F = M∙a. He действует t ли на массу М, движущуюся по окружности, сила М∙v2/R.

Оба эти вопроса являются выражением тех, реальных трудностей, которые возникли сразу же, как только люди оказались перед необходимостью объяснить движение планет по орбитам. Ответ на вопрос 2 следует из эксперимента: «Да, каждое реальное движение по окружности требует наличия реальной силы, направленной внутрь, a М∙v2/R есть величина этой силы». Чтобы тело могло двигаться по окружности, на него должна действовать сила, направленная к центру. Такая сила может осуществляться с помощью какого-либо реального внешнего воздействия — веревки, пружины или силы тяготения[82].

Пример А

Вращайте камень, привязанный к веревке (фиг. 107). Вы тянете за веревку, а веревка тянет камень к центру. Веревка буксирует камень и сообщает ему некоторое количество движения в новом направлении.

Представим себе, что веревка делает серию слабых рывков; рывок — и скорость изменила свое направление, еще рывок — снова изменение, еще, еще и так вдоль всей окружности. Если вы отпустите веревку, рывки прекратятся, прекратится и изменение скорости, а камень будет продолжать двигаться по касательной. (Сказать, что «камень улетает по касательной» — значит ввести в заблуждение).

Вращение камня на веревке по окружности, расположенной в горизонтальной плоскости, под действием пружины или веса обеспечивает наличие внутренней силы, которую можно измерить. Ниже описаны 3 опыта. Любой из них можно использовать для проверки справедливости соотношения F = M∙v2/R.

Фиг. 107. Вращение камня на веревке.

Опыт 1. Металлический шар, связанный шнуром со стальной пружиной, равномерно вращается по кругу (фиг. 108).

Пружина растягивается до некоторых пор, а затем длина R шнура + пружины остается постоянной во время вращения. Движение хронометрируется и затем рассчитывается величина силы М∙v2/R, направленной внутрь. Эта сила, фактически действующая со стороны пружины, определяется в отдельном эксперименте путем навешивания нагрузки на пружину.

Чтобы увидеть, насколько растянулась пружина при вращении, необходимо некоторое устройство.

Опыт 2. Металлический шар, привязанный к шнуру, равномерно вращается по кругу (фиг. 109).

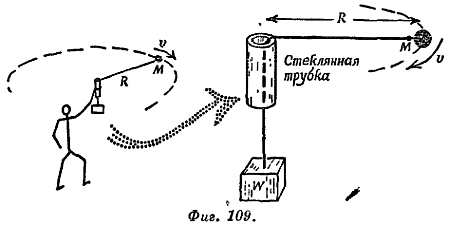
Шнур спускается вниз в стеклянной трубке с гладкими открытыми концами и оттягивается с помощью груза W. Двигая трубку по маленькому кругу, экспериментатор поддерживает движение шара по горизонтальному кругу. Движение хронометрируется, и определяется значение силы М∙v2/R, направленной внутрь. Эта сила, фактически действующая на шар со стороны шнура, является силой натяжения и практически равна (за вычетом незначительного трения) весу груза W.

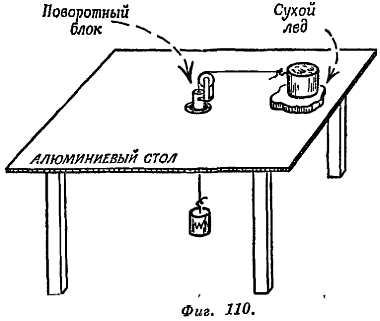
Опыт 3. В этом варианте опыта 2, когда трения нет, шар заменен тяжелым блоком, расположенным на куске сухого льда, скользящем по алюминиевому столу (фиг. 110). Шнур пропущен через отверстие в центре стола, а стеклянная трубка заменена маленьким блоком, который поворачивается в этом отверстии на очень хороших подшипниках.

Пример Б

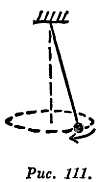
Проследите за движением «конического маятника» (фиг. 111). Гиря маятника, движущаяся по окружности в горизонтальной плоскости, подвергается воздействию двух реальных сил — веса и натяжения веревки. Если вы измерите эти силы и сложите их как векторы, вы можете найти результирующую горизонтальную силу, направленную внутрь к центру орбиты гири. Измерив параметры орбиты и время одного оборота, вы можете проверить соотношение а = v2/R

Пример В

Шарик катится внутри воронка

по эллиптической орбите (фиг. 112, а).

Пример Г

Стальной шар катится по горизонтально расположенной стеклянной пластине в магнитном поле (фиг. 112, б). На практике обычно используется электромагнит, который располагается под столом. (Магнитное поле намагничивает шар так, что он притягивается к полюсу магнита. Получая подходящее ускорение, этот шар будет кататься вокруг полюса магнита.)

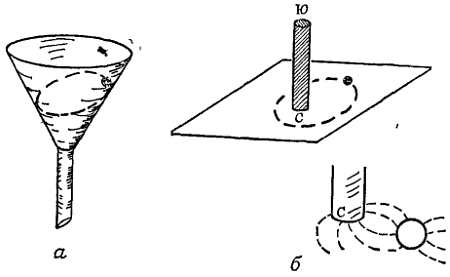
Фиг. 112. Примеры кругового движения с центростремительной силой.

а — стальной шар в стеклянной воронке; б — стальной шар на гладком столе в поле магнита.

Пример Д

Движение Луны и планет.

Задача 2

Предположим, что тело, движущееся по окружности, должно увлекаться к центру реальной силой (вызванной действием такого реального агента, как веревка, пружина, дорога). Для каждого из перечисленных ниже случаев назовите воздействие, которое обеспечивает появление необходимой силы. (Первый ответ приводится в качестве образца.)

1. Камень, вращающийся на веревке «горизонтальной плоскости. (Ответ: «Натяжение веревки» или «Его тянет веревка».)

2. а) Тележка на крутом повороте.

б) Тележка, в точке А совершающая мертвую петлю (фиг. 113).

в) Тележка, в точке В совершающая мертвую петлю (фиг. 113).

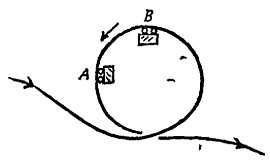
Фиг. 13. К задаче 2.

3. а) Велосипедист делает крутой поворот на ровном участке дороги (фиг. 114).

б) Велосипедист делает крутой поворот на наклонном участке пути (фиг. 114).

4. Самолет в вираже.

5. Отрицательно заряженный электрон, движущийся в атоме вокруг положительно заряженного ядра.

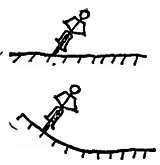
Фиг. 114. К задаче 2.

Ускорение, без изменения скорости

На заданный ранее вопрос 2 дает ответ эксперимент: движение по окружности требует направленной внутрь силы величиной Mv2/R. А теперь снова вернемся к вопросу: почему тело с ускорением, направленным к центру круга, не движется быстрее и не перемещается ближе к центру? Это все еще остается непонятным, хотя теперь начинает казаться, что дело тут скорее в формулировке, нежели в физической сущности явления. Факты очевидны: движение по окружности существует, и для его поддержания необходимы силы, направленные внутрь. Под действием этих сил происходит изменение количества движения, в результате чего траектория тела искривляется, изменяя направление скорости, но не меняя ее величины. Если мы хотим включить такие изменения скорости в определение ускорения a = Δv/Δt, to следует считать, что при движении по окружности ускорение действительно имеет место. Если же мы ограничимся прежним определением «ускорения» — «движущийся все быстрее и быстрее», тогда равномерное движение по кругу может и не сопровождаться «ускорением». Если мы станем на такую точку зрения, то должны будем ввести новую категорию сил в дополнение к тем, которые определяются соотношением

«СТАРАЯ» СИЛА = МАССА∙СКОРОСТЬ ВСЕ УБЫСТРЯЮЩЕГОСЯ ДВИЖЕНИЯ.

Для новых сил верно другое соотношение:

«НОВАЯ» СИЛА = МАССА∙(СКОРОСТЬ)2/РАДИУС

Как следует из эксперимента, эти новые силы могут быть реальными силами, которые должны обеспечить движение тела по окружности. Однако во избежание хлопот мы не станем вводить такого ограничения, а будем применять термин «ускорение» для всех видов Δv/Δt, ибо из опыта[83] следует, что во всех случаях соотношение F = M∙a характеризует результирующую силу. Исходя из этого мы должны произвести две серии проверок соотношения F = M∙a; одна из них связана с рассмотрением прямолинейного движения, а другая — с телами, движущимися по окружности.

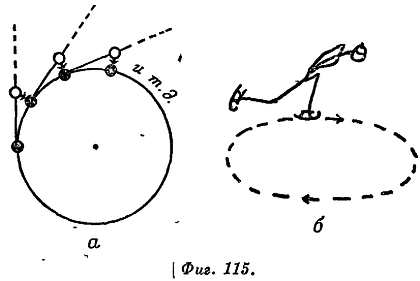
Двигаясь по окружности, тело устремляется внутрь к центру, в противном случае оно продолжало бы двигаться по касательной; уходя немного по касательной, тело притягивается к центру, и так оно движется, непрерывно стремясь внутрь, но не попадая в центр. Если такая ситуация вам кажется парадоксальной, то понаблюдайте за конькобежцем, выписывающим небольшие круги на льду, — он все время как бы падает, наклонившись вперед (фиг. 115).

На вопрос 1 следует ответить так: ускорение перпендикулярно направлению движения и поэтому не увеличивает скорости в этом направлении. Добавляясь к нулевой скорости, это ускорение увлекает тело по орбите постоянного радиуса.

Центростремительная или центробежная сила?

Сила, которая тянет тело к центру орбиты, изменяя лишь направление скорости, называется центростремительной. В противоположность этому сила, которая приводит к тому, что тело удаляется от центра, называется центробежной. Вы часто слышите эти названия, но, к сожалению, этот термин вводит в заблуждение, когда его применяют к движущимся телам. Конечно, существует направленная наружу центробежная сила, действующая на «партнера», расположенного в центре, например на человека, который держит веревку с вращающимся на ней камнем. Такой подход вносит путаницу в определение силы, действующей на движущееся тело. Поэтому термина «центробежная сила» лучше избегать. Однако, поскольку он широко распространен, особенно среди инженеров, мы должны будем вернуться к нему позднее и вкратце обсудить его значение.

Центростремительная сила. Mv2/R

Если масса М движется по окружности с радиусом R с постоянной скоростью v, то должно существовать реальное воздействие, обеспечивающее необходимую силу, равную Mv2/R (фиг. 116, а). Если результирующая реальных сил, действующих на М, больше Mv2/R, то скорость тела будет увеличиваться в направлении к центру и оно будет двигаться по свертывающейся спирали. Если действующие силы слишком малы, то траектория будет представлять собой раскручивающуюся спираль (фиг. 116, б). Существует много механических систем, в которых, как показано в приводимых ниже примерах, эта сила соответствует необходимой величине. Теперь мы подробно рассмотрим некоторые примеры движения по окружности — от камня на веревке до современной центрифуги.

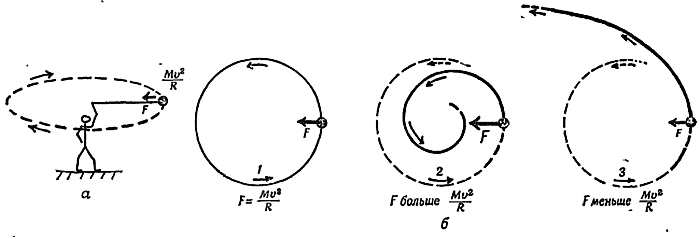
Фиг. 216. Движение по окружности

Камень вращается на веревке. Веревка растягивается до тех пор, пока ее натяжение не станет равным силе Mv2/R, тянущей внутрь.

Тележка в «мертвой петле». На тележку действует сила тяжести и сила со стороны рельсов. Если пренебречь трением, то можно считать, что сила, действующая со стороны рельсов, направлена перпендикулярно им. Продолжите это обсуждение, отвечая на вопросы задачи 3.

Задача 3

Предположим, что тележка выполняет мертвую петлю, как это показано на фиг. 117. Чтобы тележка двигалась по окружности, в точке А должна действовать некоторая сила.

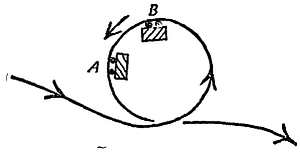
Фиг. 117. К задаче 3.

а) Какое направление должна иметь эта сила?

б) Что обеспечивает эту силу?

в) Какая другая сила (силы) должна действовать в точке А на тележку?

г) Какое влияние должна оказывать эта другая сила (силы) на движение тележки?

[Замечание. Отвечая на вопрос (г), забудьте про силы, о которых говорилось в вопросах (а) и (б). Это — реальная сила, и она должна присутствовать. Она играет особую роль. Здесь не имеет смысла заниматься сложением векторов, чтобы получить результирующую силу.]

Для движения тележки по окружности необходимо, чтобы в точке В была приложена сила.

д) Какое направление должна иметь эта сила в точке В?

е) Как обеспечивается наличие такой силы?

ж) Если тележка движется значительно медленнее, то потребуется много меньшая сила, Почему?

з) Почему сила в точке В может оказаться слишком большой? Что произойдет, если эта сила будет слишком велика?

Езда на велосипеде. Когда велосипедист движется по горизонтальному кругу, реальное воздействие должно обеспечить внутреннюю, центростремительную силу. На неровной дороге таким воздействием будет трение, оно обеспечивает горизонтальную силу, которая толкает шины в сторону. (На ледяной дорожке трение практически отсутствует и велосипедист не сможет сделать поворот, он будет проскальзывать вперед, считая, что вопреки желанию скользит в противоположную сторону.) При повороте велосипедист наклоняется вбок. Наклон сам по себе не увеличивает силы трения, но он необходим, ибо иначе сила, действующая на колеса со стороны дороги, опрокинет велосипедиста. Если он вместо прямой дороги движется по наклонному треку, то нет больше необходимости в боковой силе трения* наклонный трек отталкивает велосипедиста от своей поверхности с силой, которая имеет вертикальную компоненту, уравновешивающую его вес, и горизонтальную компоненту, которая обеспечивает необходимую центростремительную силу.

Самолеты. Пилот, совершая разворот, должен наклонить машину таким образом, чтобы давление воздуха толкало ее по направлению к центру круговой орбиты.

При повороте «подъемная сила» должна быть намного больше (это обеспечивается элеронами[84]), чем во время устойчивого горизонтального полета, когда она как раз уравновешивает вес самолета. Сам пилот тоже должен двигаться по кривой, и ему тоже необходимо некоторое направленное к центру давление. В наклоненном самолете на пилота с необходимой силой действует его кресло. А что же происходит с циркуляцией крови к голове пилота (направленной к центру виража)? Кровь должна не только участвовать в развороте, но и циркулировать от сердца к голове. Сердце должно нагнетать кровь с большим усилием, чтобы обеспечить достаточное питание мозгу, в противном случае кровь не достигнет мозга и пилот потеряет сознание или временно ослепнет. В нормальном состоянии, когда вы стоите неподвижно, ваше сердце прокачивает m килограммов крови вверх с силой (m 9,8) ньютон, чтобы обеспечить циркуляцию крови. Если самолет летит быстро (велика v) по кривой с малым R, сила, необходимая для прокачивания крови от сердца к голове, m(v2/R), может во много раз превысить (m 9,8). Сердце пилота может оказаться неспособным обеспечить эту силу m(v2/R), и тогда возможна временная слепота. Если вы ложитесь, а не стоите, нагрузка на сердце уменьшается. Если пилот не сидит в таком положении, чтобы его голова была направлена к центру кривизны его траектории, а ложится вдоль этой кривой, он может не терять сознания гораздо дольше.

Фиг. 118. Самолет делает мертвую петлю.

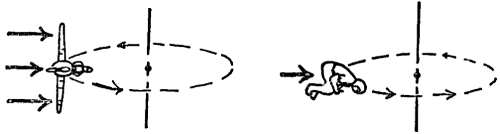
Фиг. 119. Силы воздушного давления на крылья и корпус толкают самолет по направлению к центру круга в петле и при повороте.

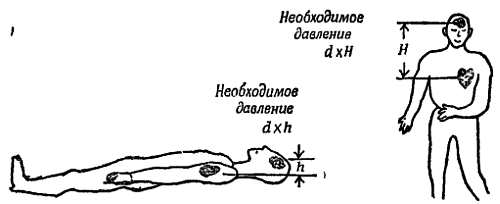
Фиг. 120. Когда человек находится в покое, стоит или лежит, сердце должно обеспечить приток крови к мозгу.

На фиг. 121 показаны результаты некоторых опытов. Центростремительное ускорение самолета v2/R выражено в единицах g.

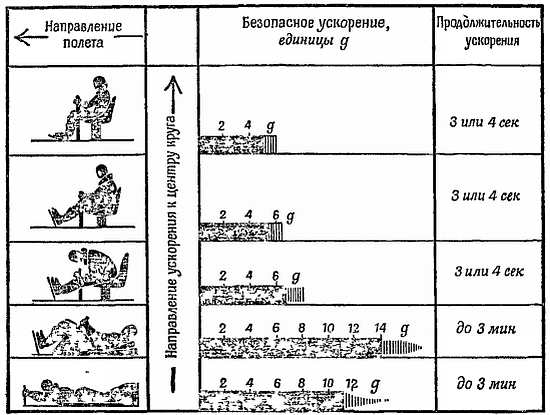
Электроны в атомах. В одной из последующих глав мы рассмотрим строение атома, считая, что электроны вращаются по орбитам вокруг ядра.

Мы предполагаем, что законы Ньютона применимы и в данном случае и что сила m∙v2/R обеспечивается электрическим притяжением.

Молочные сепараторы и центрифуги. Если вращать по кругу привязанный к веревке сосуд с жидкостью (фиг. 122), то к каждому участку жидкости будет приложена центростремительная сила m∙v2/R, ибо в противном случае сосуд не мог бы двигаться по круговой орбите. В каждом случае направленная вовнутрь сила равна

(ПЛОЩАДЬ)∙(ДАВЛЕНИЕ НА НАРУЖНОМ КОНЦЕ) — (ПЛОЩАДЬ)∙(ДАВЛЕНИЕ НА ВНУТРЕННЕМ КОНЦЕ)

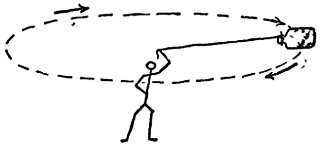
Фиг. 122.

Эти давления зависят от радиусов и скоростей, но не от содержания образца. Поэтому сила, создаваемая внешним воздействием, одинакова во всех случаях (для данного объема), но сила, необходимая для поддержания кругового движения, зависит от целостности образца, и как следствие — разделяющее действие. Некоторый участок объема жидкости (фиг. 123) движется по окружности и поэтому требует направленной внутрь результирующей силы для удержания его на круговой орбите. Такая сила должна быть обеспечена разностью давлений жидкости на его концах. Давление на внешний конец участка жидкости должно быть больше давления на его внутренний конец.

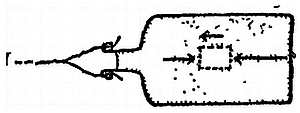
Фиг. 123.

Таким образом, имеется постепенное увеличение давления по мере приближения ко дну сосуда. Весьма похожее на обусловленный силой тяжести вертикальный перепад давления в стоящем сосуде. Однако в быстро вращающемся сосуде давление может быть намного больше. Пузырек воздуха или нечто легче жидкости будет испытывать это давление, но при очень малом m и m∙v2/R будет очень мало.

Легкое тело получило бы ускорение и увлекалось бы вовнутрь (к оси вращения). Сначала по мере движения вовнутрь тело будет двигаться ускоренно, пока не достигнет скорости, при которой внутреннее трение в жидкости в точности уравновесит дополнительную силу. Тогда

СИЛА, НАПРАВЛЕННАЯ ВОВНУТРЬ (из-за большого давления на внешнем конце) — СИЛА, НАПРАВЛЕННАЯ ВОВНЕ (из-за меньшего давления на внутреннем конце) — ТОРМОЖЕНИЕ БЛАГОДАРЯ ВНУТРЕННЕМУ ТРЕНИЮ (из-за движения жидкости вовнутрь) = РЕЗУЛЬТИРУЮЩАЯ СИЛА, (направленная вовнутрь, равна требуемой силе m∙v2/R)

Именно так получают сливки во вращающемся молочном сепараторе. На более плотные частицы, например на песчинки в мутной воде, действует такая же внутренняя сила, обусловленная давлением. Но для их удержания на круговой орбите требуется гораздо большая сила, нежели в случае пузырька воздуха; таким образом, песчинки будут двигаться по раскручивающейся спирали и попадут во внешнюю часть сосуда. Возьмем теперь сосуд с мутной водой, содержащей пузырьки воздуха. Если поставить ее на стол, муть будет оседать, а пузырьки воздуха из-за трения в жидкости медленно и равномерна двигаться вверх. Если вращать этот сосуд на веревке, то муть будет осаждаться, а пузырьки подниматься гораздо быстрее. Такие центрифуги позволяют ускорять осаждение тонких взвесей и даже разделять в воде крупные белковые молекулы.

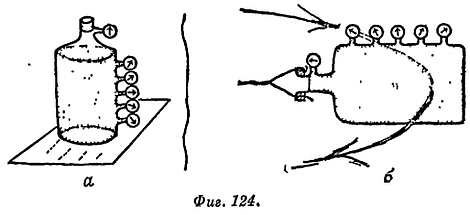
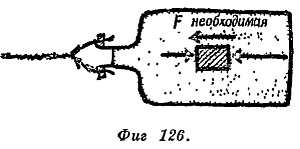
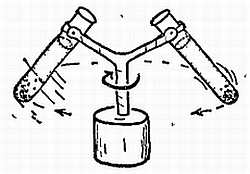
Фиг. 127. Центрифуга.

Венский вальс. Танцующая пара вращается вокруг общей оси, держась друг за друга (на одном или на обоих каблуках, фиг 128).

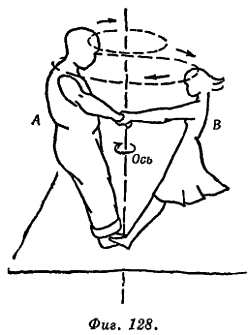
Партнеры тянут друг друга вовнутрь; эта тяга обеспечивает необходимые центростремительные силы. Даже если масса партнера А больше массы партнера В, натяжения одинаковы и противоположно направлены (третий закон Ньютона). Эта «система» так подбирает радиус своей орбиты, чтобы силы уравновешивались.

В результате партнеры вращаются вокруг оси, проходящей через их общий центр тяжести. А теперь найдем алгебраическое выражение для такого танцевального вращения (фиг. 129).

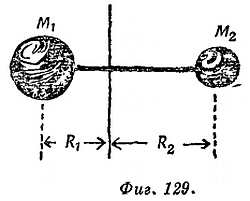
Предположим, что А и В имеют массы М1 и М2 и вращаются вокруг общей оси по окружности с радиусами R1 и R2 со скоростями v1 и v2. Оба совершают один оборот за время Т. Тогда v1 = 2πR1/T и v2 = 2πR2/T (т. е. v1/v2 = R1/R2, хотя это и не необходимо). Обе центростремительные силы должны быть равны и противоположны друг другу, так как они обусловлены действием и противодействием танцоров. Таким образом,

М1v21/R1 = М2v22/R2

или

М1∙(2πR1/T)2/R1 = М2∙(2πR2/T)2/R2

т. е. М1R1 = М2R2 [сокращая ∙(2π)2, Т2 и т. д.]. Тогда произведение (масса)∙(расстояние от оси вращения) будет одинаково для обоих партнеров. Поэтому более тяжелый партнер располагается на меньшем расстоянии от оси. Если вы посмотрите, что сказано о нахождении положения центра тяжести двух тел в пособиях по физике, то найдете, что если R1 и R2 измерять от оси, проходящей через центр тяжести М1 и М2, то М1R1 должно быть равно М2R2 в соответствии со свойствами центров тяжести. Тогда для вращающихся систем М1R1 = М2R2 Именно поэтому танцующая вальс пара должна вращаться вокруг ее центра тяжести.

Подобное рассмотрение правильно описывает танцы с точки зрения физики, но вряд ли это практически полезна. Оно верно и в случае движения Луны и Земли и важно для понимания природы приливов. Астрономы используют его при рассмотрении движения двойных звезд. Вы встретите и другие примеры проявления центростремительной силы в астрономии и атомной физике.

Центробежная сила и средство от головной боли для инженеров

Движение по окружности требует реальной силы, направленной вовнутрь и производимой реальными внешними воздействиями. Представление о центростремительной силе поможет вам разобраться во всех проблемах, связанных с круговым движением. А вот что такое центробежная сила? Вы часто слышите это слово, даже сами его произносите, когда вам приходится вращать что-либо по кругу, вы найдете этот термин во многих книгах по физике. Существует множество мнений о том, что такое центробежная сила. Вы можете выбрать из них то, которое вам больше по вкусу.

МНЕНИЕ I: Центробежная сила — это ложная сила, представление о которой возникло на основе неправильного толкования запутанного взаимоотношения между воздействием, определяющим силу, и объектом приложения этой силы.

Если вы вращаете камень на веревке, ее натяжение тянет вашу руку наружу с той же силой, с какой тянет и камень внутрь. Это — настоящая центробежная сила, действующая на вашу руку, но не на вращающийся камень. Вы ощущаете, что вашу руку что-то тянет наружу и говорите: «Я чувствую, что камень и веревка оттягивают мне руку. Это свидетельствует о том, что центробежная сила тянет камень и веревка передает действие этой силы». Вот тут вы и ошиблись. Не существует никакой силы, действующей на камень. На самом деле веревка, оттягивая вашу руку наружу, в то же время тянет камень вовнутрь. Существует лишь одна действительная сила — центростремительная, тянущая камень вовнутрь

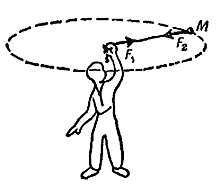
Фиг. 130. Центробежная сила?

Представьте себе, что вы собрались посетить аттракцион в парке и покататься на вращающемся полу. Вы и ваш спутник входите в помещение и садитесь на неподвижный полированный пол. Зная, в чем суть представления, вы прижимаетесь покрепче к полу» Когда пол начнет вертеться, вам покажется, будто какая-то неведомая сила отбрасывает вас от центра, и если бы не сцепление с полом, под действием этой силы вы стали бы скользить к ограждению.

Ваш спутник тоже заскользит к краю, если вы не удержите его, подтягивая к центру. Вы оба будете чувствовать, что боретесь с «центробежной силой». Но предположим теперь, что на вас смотрит неподвижный наблюдатель. Если смотреть на вращающуюся комнату извне, то будет казаться, что вы оба движетесь по круговой орбите и для удержания Вас на этой орбите необходимы реальные силы. Для вашего товарища это будет сила, действующая с вашей стороны и направленная вовнутрь, а для вас — это сила сцепления с полом. Повторим еще раз: вы просто воображаете, что существует некая сила, действующая извне на вашего товарища, поскольку вы уже приложили к нему реальную силу. С точки зрения постороннего наблюдателя эта внутренняя сила вовсе не компенсируется какой-то таинственной внешней силой; именно внутренняя «ила и обеспечивает ускорение вовнутрь и определяет ваше движение по кривой. Если вы отпустите вашего спутника, он при отсутствии трения будет двигаться по касательной. Его последовательные положения на касательной будут лежать все дальше и дальше от центра круга, так что вам, поскольку вы вращаетесь вместе с полом, будет казаться, что ваш товарищ скользит вдоль радиуса. На самом же деле он продолжает двигаться по прямой (по касательной) — это простой пример, иллюстрирующий первый закон Ньютона.

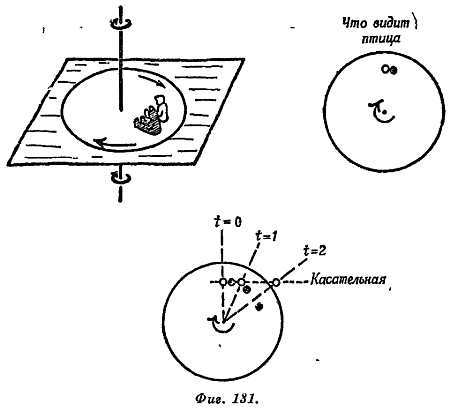
МНЕНИЕ II: Центробежная сила — заблуждение, проистекающее от того, что мы существуем во вращающейся системе, но пытаемся забыть об атом.

Из приведенного случая с вращающимся полом можно сделать следующий вывод. Для человека, сидящего на столе и не знающего, что он движется, существует внешнее силовое поле, наделяющее каждую массу М внешней силой Mv2/R. Независимо оттого, существует ли реальное внешнее воздействие, прилагающее силу, направленную вовнутрь для уравновешивания силы, направленной вовне, будет казаться, что любое тело, предоставленное самому себе, скользит наружу с ускорением v2/R. Становясь на точку зрения постороннего наблюдателя, следует считать и силовое поле, и скольжение наружу лишь кажущимися и обусловленными тем, что, пребывая во вращающейся системе, мы тем не менее забываем принимать в расчет ее движение.

МНЕНИЕ III: Средство от головной боли для инженеров.

Это прекрасное применение центробежной силы. Давайте строго отнесемся к слабо подготовленному молодому инженеру, который предпочитает статику — физику покоя (или равновесия) динамике, т. е. физике движения. Задачи, включающие ускорение и вращение, вызывают у него головную боль, и он хочет свести эти задачи к простым статическим силам, которые действуют в конструкциях мостов и подъемных кранов и в которых он хорошо разбирается. Это действительно можно сделать. Рассмотрим задачу о вращении конического маятника (фиг. 132).

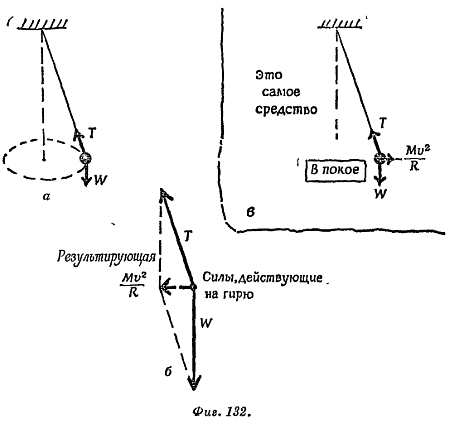
На груз маятника действуют две реальные силы: его вес и сила натяжения веревки. Эти две реальные силы складываются и дают результирующую силу, направленную вовнутрь, Mv2/R, в противном случае груз не смог бы продолжать движение по круговой орбите. Значит, имеются две силы W и Т, которые дают направленную вовнутрь горизонтальную результирующую силу Mv2/R. Превратим эту задачу в статическую (т. е. в задачу с нулевой результирующей силой) путем добавления некоторой дополнительной фиктивной силы. Какую фиктивную силу нужно добавить к W и Т, чтобы результирующая сила обратилась в нуль? Эта сила должна быть равна — Mv2/R, или силе Mv2/R, направленной наружу. Некоторые профессора могут сказать этому инженеру: «Да, вы можете обратить любую задачу с круговым движением в статическую, еслико всем реальным силам добавите некую фиктивную центробежную силу Mv2/R и напишете уравнение, доказывающее, что все силы (включая фиктивную) дают в сумме нуль. Решение этого уравнения дает вам ту же самую информацию, что и метод, учитывающий только реальные силы, которые создают направленное вовнутрь ускорение, v2/R.

При таком подходе центробежная сила, несмотря на то что она фиктивна, тем не менее вполне пригодна для лечения головной боли у инженеров. Точно так же в качестве средства спасения от трудностей она используется в современной физике, но в этом случае это лишь полезный искусственный прием. Такой подход, которым пользуется большинство студентов, дает правильный ответ, но теория становится более трудной для понимания. В самом деле, ведь при этом реально существующее движение сводится к фиктивному покою. Тот, кто, введенный в заблуждение правильным ответом, отнесется с доверием к такому приему, будет чувствовать себя неуверенно, не зная, какая из этих сил реальна и как она действует. Если вы стремитесь к настоящему пониманию физики, то любой ценой избегайте этого лекарства от головной боли. И уж, конечно, не смешивайте это «центробежное-лекарство-от-головной-боли» с центростремительными силами, иначе получится чепуха!

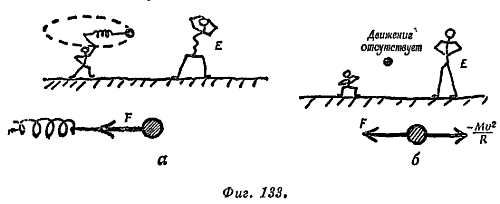
МНЕНИЕ IV: Относительность.

Это мнение представляет собой несколько замечаний к очень извращенной теории относительности. Прочтите этот абзац для развлечения или сочтите его на некое предупреждение, но не превращайте его в нечто, похожее на средство от головной боли у инженеров. Взгляды, связанные с представлением об относительности движения, правильны, но только в системе определений, специально для этого сформулированных.

Разве нельзя оказать что-либо более положительное о центробежной силе? Некоторые ученые (см. мнение II) спрашивают. «Почему нехорошо наблюдать за предметами из вращающейся системы координат? Ведь в конце концов мы живем на вращающейся Земле Действительно ли «центробежные силы», возникающие из представлений, связанных с нашей вращающейся системой, отличаются от других сил, и так ли они нереальны? Разве можем мы быть уверены в том, что происходит на самом деле — вращаемся мы или кто-нибудь другой?» (Здесь мы вновь возвращаемся к временам Коперника и Птолемея.) Этот последний вопрос напоминает задачу с ускоряющимся железнодорожным вагоном, на примере которого проверялись законы Ньютона. Соорудив наклоненную комнату в таком вагоне, мы все же нашли бы те же самые законы: «тяготение», изменяющееся по величине и направлению. Мы догадываемся о том, что не можем обнаружить различия между эффектами, вызванными ускорением и силой тяжести. Эйнштейн построил общую теорию относительности на основе детального рассмотрения невозможности установить это различие.

Теория относительности начинается с заявления, представляющего собой аксиому и состоящего в том, что мы не можем сказать, кто именно движется — мы сами или «кто-то другой», что не существует такого понятия, как абсолютное движение. Если это так, то выражение «абсолютное пространство» бессмысленно, оно не необходимо и не должно употребляться в науке. В таком случае рабочей геометрией «пространства» должна быть такая геометрия с помощью которой мы могли бы открыть те же самые физические законы независимо от того, что мы думаем о нашем движении, т. е. движемся ли мы или кто-либо другой. Что заставляет нас видоизменять ту простую геометрию пространства и движения, которую предложил Евклид и которой пользовались Галилей и Ньютон. Было сделано много неудачных попыток для выделения абсолютного движения (в случае постоянных скоростей), даже с помощью световых сигналов, поэтому мы чувствуем, что вправе принять принцип относительности и его видоизмененную геометрию. В практической жизни эти видоизменения незаметны. Они начинают играть роль лишь при очень больших скоростях, например в астрономии и в атомной физике. Распространяя принцип относительности на случай ускоренного движения, мы полагаем, что расположенный в определенном месте наблюдатель не сможет установить различия между эффектами, связанными с ускорением, и изменением силы тяжести в данном месте, таким образом, мы приходим к выводу, что гравитационные поля могут рассматриваться в качестве местных (локальных) изменений геометрии пространства-времени. Это и есть принцип эквивалентности Эйнштейна. Хотя такой подход является совершенно новым, практически он дает малые отклонения от закона всемирного тяготения Ньютона.

Распространяя эту идею на случай вращения, мы предполагаем, что локальный наблюдатель не может заметить различия между эффектами, связанными с вращением системы координат, и локальным изменением силы тяжести, если он движется вместе с системой. В этом случае тянущая наружу центробежная сила будет представляться ему (находящемуся на вращающемся полу) вполне реальной, дополнительной горизонтально направленной силой тяги, или силой тяжести. Для жука, помещенного в центрифугу, центробежная сила будет проявляться в качестве реального поля силы тяжести, только в тысячи раз более сильного, нежели обычная сила тяжести. Для жука сила тяжести будет направлена иначе — он забудет о ее прежнем направлении — и будет неизмеримо больше. Принципы общей теории относительности оказались очень полезными для координации мышления, и за все время не наблюдалось каких-либо противоречащих им явлений. С этой точки зрения центробежная сила вполне приемлема. Если мы хотим проверить эффекты, связанные с большими гравитационными полями, недостижимыми в условиях притяжения Земли, то можем воспользоваться, центрифугой.

Общий принцип эквивалентности запрещает нам называть те виды движения^ которых участвует Земля, абсолютными и заставляет использовать новую механику и геометрию, с помощью которых можно предсказать одни и те же эффекты независимо от того, вращается ли Земля вокруг Солнца или же звезды и Солнце вращаются вокруг Земли. Согласно общей теории относительности, вращающаяся Вселенная будет порождать «центробежные силы» на неподвижной Земле, так что невозможно выяснить (с помощью маятника Фуко или изменения величины g с широтой), вращается ли Земля или вращается то, что ее окружает. Поэтому, возвращаясь к старому вопросу: «Кто прав — Коперник или Птолемей?», мы должны в отличие от Галилея сказать: «Обе точки зрения допустимы, хотя одна из них представляет собой более простое описание явлений, пригодное для практического мышления и работы». Пред нами пример гегелевской идеи развития: тезис — антитезис — синтез.

А ваше мнение об этих четырех случаях?

Сделайте сами выбор. Однако при разборе задач и экспериментов, приведенных в этой книге, советуем пользоваться только центростремительными силами.

ЛАБОРАТОРНЫЙ ОПЫТ

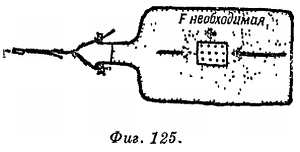
Опыт 4. Простая проверка соотношения «Необходимая сила = Mv2/R»

Вместо сложного устройства, которое можно приобрести вместе с инструкцией типа поваренной книги, где даются рецепты студентам, как «проверить этот закон», мы предлагаем некое приспособление, предназначенное для грубой, но наглядной проверки. Попытайтесь произвести эту проверку с помощью партнера. Если измерения и расчеты не ясны, обратитесь к здравому смыслу и обдумайте все, прежде чем просить о помощи. Сначала внимательно выслушайте воображаемый расчет прибора, который начиняет изобретать исследовательская группа, состоящая из следующих лиц: руководитель Сагредо, главный экспериментатор Сальвиати и его ассистент и критик Симпличио. (Этот прибор был разработан в результате ряда обсуждений с использованием промежуточных экспериментов, в которых проверялась пригодность предлагаемых конструкций.)

САГРЕДО. Мы хотим проверить предсказание о том, что движение по кругу требует некоторой силы, направленной вовнутрь и определяемой соотношением F = Mv2/R. Мы предлагаем крутить на веревке камень и измерять ту реальную силу, с помощью которой мы удерживаем камень на орбите. Затем мы сравним эту силу о той, которая предсказывается соотношениями a = v2/R и F = M∙а.

СИМПЛИЧИО. Нам необходима очень сложная аппаратура: измеритель скорости v.

САЛЬВИАТИ. Вздор. Просто измерьте время одного оборота. Тогда v будет равно длине окружности 2πR, деленной на это время.

СИМПЛИЧИО… и сложный прибор дли измерения силы.

Фиг. 135

САГРЕДО. Неверно. Ведь мы хотим выполнить совсем простую проверку.

САЛЬВИАТИ. Используйте для измерения натяжения веревки пружину. Позже мы сможем определить эту силу, подвешивая пружину и нагружая ее до тех пор, пока растяжение не станет таким же, как при вращении. Мы знаем, что хорошая стальная пружина надежна.

САГРЕДО. Простак! Если так слепо доверять законам, то вы должны помнить об их ограниченности. Знаете ли вы, что пружины могут растягиваться больше, чем это следует из закона Гука?

СИМПЛИЧИО. Мы можем остановить растяжение пружины, связывая ее концы длинной нитью.

САГРЕДО. О, прекрасно! И тогда, когда эта нить будет свободна, она не нужна; а когда ее натянут туго, она испортит наш эксперимент, внося дополнительное натяжение; так мы и не будем знать истинного натяжения.

САЛЬВИАТИ. Я думаю, что мы все же можем использовать предложение Симпличио. Нам как раз нужно знать, как сильно растягивается эта пружина во время вращения, чтобы потом, нагружая ее, мы могли довести ее до такого же растяжения. Если мы соединим концы пружины нитью, как это предложил Симпличио, мы будем вращать камень все быстрее и быстрее до тех пор, пока нить не окажется натянутой. Это мы можем назвать «стандартным растяжением».

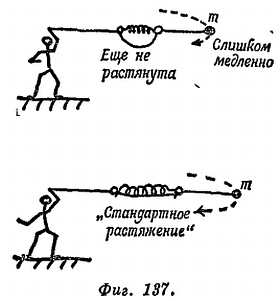
СИМПЛИЧИО. Ну ладно, так мы найдем массу и скорость, но как мы измерим R? Удержим ли мы линейку около вращающейся пружины?

САЛЬВИАТИ. Можно измерить R позже, когда пружина будет подвешена вертикально и нагружена до стандартного растяжения.

СИМПЛИЧИО. Я понимаю смысл предложения о стандартном растяжении; но если при этом пружина натянется до предела, вновь будет в силе ваше возражение против предложенной мной нити — сила, добавляемая пружиной, будет неизвестна.

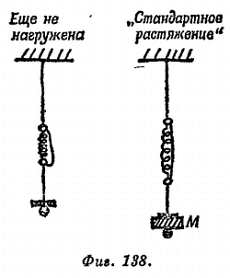
САЛЬВИАТИ. Почти до предела.

СИМПЛИЧИО. Я не понимаю, как мы определим, что пружина натянута почти до предела.

САЛЬВИАТИ. Давайте тогда используем другую, маленькую пружинку, привязанную к нити. Эта маленькая пружинка остается в нерастянутом состоянии, пока большая пружина не натянется туго.

СИМПЛИЧИО. Нужно ли измерять и натяжение маленькой пружинки?

САЛЬВИАТИ. Нет; маленькая пружинка служит только индикатором. Она не будет тянуть до тех пор, пока не начнет растягиваться, а натяжение ее будет столь мало, что создаваемая ею сила незначительна.

СИМПЛИЧИО. Даже я понимаю, что это становится ужасной неразберихой. Маленькая пружинка будет задевать за главную пружину.

САЛЬВИАТИ. Будет лучше, если мы поместим эту маленькую пружинку внутри главной пружины, а не будем протягивать ее снаружи.

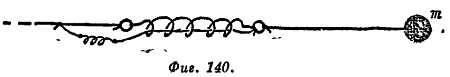
СИМПЛИЧИО. Боюсь, что мы испортим маленькую пружинку, прежде чем сможем провести измерения. Мы будем крутить очень быстро и безнадежно растянем ее.

САГРЕДО. Хорошо, но вы уже предлагали средство против этого.

СИМПЛИЧИО. Да, воспользуйтесь снова моим предложением. Свяжите концы этой маленькой пружинки нитью.

САГРЕДО. Хорошо. Тогда мы сможем крутить все быстрее и быстрее, пока не заметим, что маленькая пружинка растянулась ровно наполовину; этим и будет определяться стандартное растяжение главной пружины.

САЛЬВИАТИ. Раскручивать будет легче, если мы привяжем основную бечевку к большому кольцу и наденем это кольцо на вертикально расположенную палку, которую экспериментатор держит в руке. Мы можем предотвратить соскальзывание кольца, добавив две шайбы и два гвоздя.

САГРЕДО. Теперь у нас есть, приспособление, которое стоит испытать.

СИМПЛИЧИО. Но мы еще не использовали закон Гука.

САГРЕДО. Мы в нем не нуждаемся. Мы просто подвесим пружину и измерим нагрузку, которая растягивает пружину до той же длины, что и во время вращения. Экспериментаторы должны потренироваться для того, чтобы вращать как раз с той скоростью, при которой маленькая пружинка окажется растянутой ровно наполовину; тогда они могут замерять время. После этого можно подвесить пружину вертикально и измерить ее натяжение при стандартном растяжении, нагружая ее. При этом можно одновременно измерить радиус орбиты — измерить R на подвешенной вертикально и нагруженной пружине.

СИМПЛИЧИО. О, так мне не придется все время бегать с линейкой.

САЛЬВИАТИ. Конечно нет, но вы можете помочь при измерении R. Боюсь, что центральный колышек не будет стоять неподвижно: экспериментатору, поддерживая вращение, придется двигать его по маленькому кругу. Наблюдая за этим, вы можете прикинуть из измерений на подвешенной пружине во время вращения, сколько надо добавить или вычесть, чтобы получить правильное значение радиуса.

СИМЦЛИЧИО. Но это еще больше, усложняет задачу. Теперь наше приспособление уже ненадежно. Я не верю в то, что мы сможем гарантировать точность измерений и сделать желаемую проверку.

САЛЬВИАТИ. А я смогу, если попрактикуюсь и буду очень внимательным.

САГРЕДО. Думаю, что оба вы ошибаетесь. Имелось в виду сконструировать простой прибор. Измерения будут приближенными. Но если выражение Mv2/R является точным, тогда различия между непосредственно измеренной силой и силой, рассчитанной из Mv2/R, будут обусловлены случайными ошибками измерения. Отклонения будут одинаково часты в одну и в другую сторону. Группироваться они будут вблизи нуля, если эксперимент делается много раз, предпочтительно разными наблюдателями. Я предлагаю просить большую труппу экспериментаторов, работающих попарно, испытать наш прибор. Пусть каждая пара выражает разницу между измеренной и «вычисленной» ими силой в процентах от ее величины. Изучая эти отклонения, мы узнаем, удалась ли наша проверка.

САЛЬВИАТИ. Мы даже сможем грубо оценить величину отклонений, обусловленных допустимыми ошибками эксперимента. Например, если один оборот совершается за 2 сек, то два экспериментатора могут замерить серию из двадцати оборотов несколько раз. Вряд ли они ошибутся более чем на несколько десятых долей секунды при полном измеряемом времени 40 сек, ошибка будет, скажем. 0,2 сек за 40 сек, или 2 сек за 400 сек, или 0,5 сек за 100 сек, т. е. 0,5 %. Время одного оборота используется для получения v, a v содержится в Mv2/R дважды. Таким образом, ошибка в измерении времени дает вклад 0,5 % + 0,5 % = 1 % в возможную ошибку Mv2/R. Мы можем оценить возможные ошибки, проистекающие из других ошибок измерения.

САГРЕДО. Пусть уже экспериментаторы сделают это сами. Тогда они больше узнают о достоверности своих результатов[85].

Задача 4

Из геометрии следует, что точка (или небольшое тело), движущаяся в постоянной скоростью v no кругу радиусом R, имеет центростремительное ускорение v2/R. Напишите геометрический вывод этого выражения. (Вы можете предположить, что скорость и ускорение — векторы, т. е. подчиняются законам геометрического сложения и вычитания. Вы можете пользоваться свойствами подобных треугольников. Дайте большие, очень четкие эскизы: один — для фактической картины, другой — для векторов.)

Задача 5

В предлагаемых ниже вопросах предполагается: 1) центростремительное ускорение равно v2/R и 2) в случае этого движения F = M∙a. (Вспомним, что всякий раз, когда вводится F = M∙a, сила должна быть выражена в ньютонах, если масса выражена в килограммах.)

а) Камень массой 2,00 кг вращается (с помощью веревки) по горизонтальной поверхности стола без трения. Длина веревки 4,0 м, следовательно, круг имеет радиус, равный 4 м. Камень движется по орбите со скоростью 7,00 м/сек. Рассчитайте ускорение камня, натяжение веревки. Приведите краткие пояснения.

б) Предположим, что веревка разрывается как pas при том натяжении, которое ей определили выше. Какова будет разрывающая сила в килограммах силы, кГ?

в) Как и в вопросе (а), камень массой 2,00 кг вращается по кругу на веревке длиной 4,0 м, но с такой скоростью, что он совершает пять оборотов ее 2 сек.

Рассчитайте его скорость (ответ оставьте в виде сомножителей, не подставляя численного значения π).

Рассчитайте натяжение каната. (Укажите единица измерения в ответе. Можно положить π2 = 10.)

Задача 6

Веревка, подвешенная вертикально, может выдержать только 10,0 кг и рвется при малейшем увеличении нагрузки.

а) Какова разрушающая сила в килограммах силы?

б) Какова эта разрушающая сила в ньютонах?

Кусок такой веревки длиной 1,00 м используется для вращения камня массой 2,0 кг по горизонтальному кругу все быстрее и быстрее, пока веревка не разорвется.

в) Рассчитайте максимальную скорость камня на орбите и приведите краткое объяснение, как вы выполнили этот расчет.

Фиг. 145. К задаче 6.

Задача 7

Игрок с ракеткой, на которой находится мяч, крутит ракеткой перед собой. Объясните, каким образом такое движение не позволяет мячу упасть.

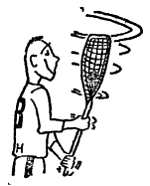
Фиг. 146. К задаче 7.

Задача 8

Самолет, летящий со скоростью 600 фут/сек (410 миль в час), преследует маленький самолет, летящий со скоростью 300 фут/сек. Маленький самолет поворачивает и удаляется по горизонтальному полукругу; самолет-преследователь старается нагнать его. Пилот может выдержать ускорение только до 5 g.

а) Рассчитайте радиус наименьшего полукруга, который пилот маленького самолета может благополучно выполнить при скорости 300 фут/сек.

б) Как долго (примерно) будет двигаться по своему полукругу маленький самолет?

в) Вычислите радиус наименьшего полукруга, безопасного для самолета-преследователя,

г) Где будет находиться самолет-преследователь, когда маленький самолет уже закончит свой полукруг (обозначьте его путь на эскизе)?

Задача 9. Вариант вывода соотношения а = v2/R (метод Ньютона)

Если тело движется по окружности от А до В, рассмотрите его как падающее тело с постоянным ускорением, направленным вниз. За время t оно пролетит с ускорением а расстояние h от той точки, в которой оно раньше покоилось.

а) Напишите уравнение для а через h и t, предполагая, что а постоянно.

б) Используя геометрическое свойство хорд круга, напишите уравнение, в котором h было бы выражено через другие измеряемые величины, приведенные на диаграмме.

в) Подставьте выражение для h в уравнение, полученное в вопросе (а).

г) Представьте, что В движется все ближе и ближе к А. Если В —> А, то горизонтальное расстояние х —> к дуге 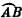 и, поскольку В —> А, хорда MN —> к диаметру 2R. Внесите эти изменения в выражение для ускорения.

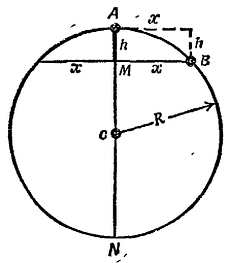
Фиг. 147. К задаче 9.

Задача 10. Центрифугирование

а) Центрифуга вращает пробирку по кругу со средним радиусом 1 фут со скоростью 5000 оборотов в минуту; содержимое пробирки находится при этом в силовом поле, во много раз большем g. Во сколько раз большем g?

б) Образец мутной воды содержит частицы, размер которых примерно равен размерам, кровяных шариков (диаметр 10-5 м). Если пробирка расположена вертикально, частицы падают на дно с постоянной скоростью ~ 1/4 дм/мин. Таким образом, объем жидкости высотой 4 дм полностью очистится примерно зa 1/4 часа. (Эти частицы не осядут все на дно. Диффузия, связанная, с броуновским движением, поддерживает некоторое их количество во взвешенном состоянии.) За какое время тот же образец станет прозрачным в центрифуге, обеспечивающей ускорение, определенное в вопросе (а)?

в) Белковые молекулы [диаметр которых в несколько сотен раз меньше диаметра частичек мути, о которых говорится в вопросе (б), но велик по сравнению с диаметром других молекул, скажем соли или воздуха] осаждаются в воде примерно в 300 000 раз медленнее, чем частички мути (вопрос б). За какое время станет прозрачной помещенная в центрифугу 4-дюймовая пробирка, содержащая суспензию таких белковых молекул в воде?

г) Если, эту белковую суспензию не помещать в центрифугу, она никогда не станет прозрачной. Почему?

д) Если известна плотность частиц, то, исходя из спорости прояснения жидкости, можно определить диаметры частиц. (Сила торможения маленькой сферы пропорциональна ее радиусу и скорости.) Частички грязи (вопрос б) могут быть измерены с помощью микроскопа, молекулы же белка увидеть невозможно. «Химические» измерения (осмотическое давление) показывают, что молекулы белка в 106 раз тяжелее атома водорода. Какая важная информация о строении атома может быть получена с помощью измерений на центрифуге?