Нашлась решетка и для рентгеновских излучений

Нашлась решетка и для рентгеновских излучений

Но нашлась дифракционная решетка и для рентгеновских излучений. Сама природа пришла здесь на помощь.

В конце XIX и начале XX века физики усиленно изучали строение твердых тел. Известно, что многие твердые тела являются кристаллами. Атомы в кристаллах расположены строго правильными рядами. Они составляют как бы естественные решетки. На рис. 31 изображена часть кристаллической" решетки поваренной соли.

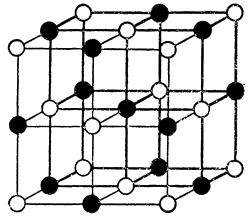
Рис. 31. Так располагаются атомы в кристалле поваренной соли. Белыми шариками обозначены атомы натрия, черными — атомы хлора. Расстояния между слоями атомов около трех ангстрем

Русский ученый Е. С. Федоров еще в 1891 году опубликовал исследование «Симметрия правильных систем фигур», в котором теоретически рассчитал, какие кристаллические формы могут встретиться в природе. Он нашел 230 возможных форм. Почти три четверти века прошло с тех пор. Наука подтвердила все вычисления ученого, и новых форм кристаллов действительно найдено не было.

Зная формы кристаллов, физики вычислили, каковы расстояния между слоями атомов в кристаллических решетках. Оказалось, что эти расстояния равны примерно одному ангстрему. Эта величина сравнима с размерами атома. Такую частую штриховку нельзя нанести никакой делительной машиной.

Кристаллы и были использованы в качестве дифракционной решетки для рентгеновских излучений. В этой решетке «преграды» и «щели» — это сами атомы и промежутки между ними. А атомы лежат не на плоскости, а расположены в пространстве. Но рассчитать дифракцию от такой решетки можно. В 1912 году физики подвергли кристалл рентгеновскому облучению и получили его дифракционный спектр. Природа рентгеновских излучений была установлена: это электромагнитные излучения, как и радиоволны, как и видимый свет.

Два крупных физика-кристаллографа — русский ученый Ю. В. Вульф и англичанин В. Брэгг одновременно установили, как можно рассчитать длину волны рентгеновских излучений, если известно расстояние между слоями атомов в кристаллической решетке и дана самая картина спектра. Формула, выражающая эту связь, называется формулой Вульфа — Брэгга.

На примере развития техники спектрального анализа видно, что по мере того, как возникают трудности и ставится новая задача, находятся и пути ее разрешения.