Бозе замыкает круг

В начале 1920-х годов понятие кванта света, который с 1926 года стали называть фотоном, было хорошо изучено. Экспериментальные факты доказали, что при повышении уровня энергии свет взаимодействует с материей, как если бы состоял из частиц с энергией Е = hv и импульсом р = hv/c. Эта уже зрелая концепция позволяла переформулировать квантовые основы закона излучения Планка.

В июне 1924 года Альберт Эйнштейн получил письмо, датированное 4 числом того же месяца и написанное молодым индийцем Шатьендранатом Бозе. В письме автор просил Эйнштейна высказать свое мнение относительно возможности публикации в немецком журнале Zeitschrift fur Physik («Физический журнал») прилагаемой к письму статьи и в случае одобрения просил перевести статью с английского на немецкий — этот труд Бозе не мог взять на себя.

Работа Бозе, которую Эйнштейн сам перевел и отправил в журнал, представляла новый вывод закона Планка о спектральном распределении излучения черного тела. Статья вышла в печать с пометкой Эйнштейна в конце: «По моему мнению, вывод Бозе формулы Планка имеет очень важное следствие. Использованный метод дает квантовую теорию идеального газа, которую я еще разработаю в деталях».

Для того чтобы понять значение нового обоснования Бозе, нужно вспомнить основные этапы доказательства Планка. Во- первых, Планк представил, что на стенках излучающей полости имеются заряженные осцилляторы, поглощающие и испускающие электромагнитную энергию. В тепловом равновесии осцилляторы испускали столько энергии, сколько поглощали, что позволило Планку установить отношение между средней энергией осциллятора U_v и электромагнитного поля u_v, которое мы рассматривали ранее:

u_v = (8???/c?)U_v.

Во-вторых, Планк должен был определить, сколько энергии соответствовало каждому осциллятору в зависимости от частоты и температуры полости. Для этого он воспользовался понятием энтропии, вероятностью Больцмана и квантовой гипотезой. Рэлей и Джинс вывели тот же показатель

8???/c?

на основании другого умозаключения. Бозе подчеркивает во введении к своей статье, что Планк и Рэлей использовали классические аргументы. Он же видел противоречие в применении термодинамики для доказательства одной части закона и квантовой гипотезы — для расчета энтропии и завершения термодинамического расчета. Поэтому Бозе предложил квантовый подход:

8???/c?.

Вспомним, что Эйнштейн уже в своей статье 1905 года доказал: энтропия излучения черного тела для низкой плотности похожа на энтропию газа, состоящего из частиц. Бозе берется за эту идею и доказывает, что излучение в полости ведет себя подобно газу — фотонному газу. Так мы забываем о волнах Рэлея и осцилляторах Планка. Учитывая, сколько механических состояний возможно для частиц, соответствующих квантовой теории и выражению де Бройля, Бозе обнаруживает искомый показатель.

До конца не осознавая этого, Бозе обращается с квантами света как с неотличимыми друг от друга частицами. Это целостная квантовая характеристика, физическое следствие принципа неопределенности.

Квантовое распределение

Бозе и Планк использовали иную форму подсчета состояний, которая отличалась от примененной первоначально Больцманом. В одной из своих статей о статистической интерпретации энтропии Больцман задается вопросом, сколькими способами можно распределить N молекул между разными состояниями энергии. Для Больцмана молекулы были различимы, было важно, имеем мы дело с молекулой 1 с энергией Е₁ и молекулой 2 с энергией Е₂, или наоборот. В то же время Планк разделяет неразличимые энергетические уровни, равные величине U_v, между числом N различимых осцилляторов. Бозе распределяет неразличимые фотоны в момент U_v/c между вероятными механическими состояниями. Подсчеты молодого индийского ученого и Планка практически идентичны и даже при разной интерпретации приводят к одному результату. Мы сможем понять разницу между способами подсчета, если представим четырех игроков, которым мы раздадим четыре карты, каждому по одной. Для Больцмана четыре карты были бы разными, например четыре туза, и существовало бы (возможность выбрать четыре карты для первого игрока, три — для второго, две — для третьего, одну — для последнего) 4-3-2-1 = 24 способа сдачи, это 24 разные партии. Для Планка и Бозе все четыре карты были бы одинаковыми, и была бы возможна всего одна партия. Планк и Бозе, не осознавая этого, играли с Больцманом в разные игры. Эйнштейн, прочитав статью Бозе, также включился в игру по квантовым правилам. Благодаря этим правилам Эйнштейн открыл законы квантового газа и предсказал явление конденсата Бозе — Эйнштейна — новое состояние материи при сверхнизких температурах, которое было экспериментально доказано в 1995 году и сейчас является важным полем исследований.

Классическая партия

Квантовая партия

Как мы увидели, квантовые частицы не имеют определенной траектории, и когда две идентичные частицы вступают во взаимодействие, например при столкновении, мы не можем проследить за ними или различить их. Корпускулярно-волновой дуализм позволяет интуитивно интерпретировать это свойство: если две частицы отдалены друг от друга и соответствующие им волны не накладываются, мы можем считать частицы отдельными объектами. При взаимодействии волны создают помехи и взаимно накладываются, поэтому невозможно с точностью сказать, где находится одна частица, а где — вторая. После окончания взаимодействия мы можем вновь говорить о двух частицах, хотя и не будем знать, какая из них где. На схеме показана разница между классическим вариантом столкновения частиц, после которого обе частицы различимы, и квантовым понятием интерференции, препятствующим различению.

В статье, написанной в том же году, Эйнштейн обобщил статистику Бозе до случая газа с материальными частицами (вместо фотонов), выводя отсюда законы квантового газа. Статья Бозе положила конец поискам обоснования закона Планка через общие принципы. Эйнштейн, Эренфест и особенно Поль Дирак отшлифовали детали и четче выразили гипотезы Бозе, подразумеваемые в статье. Следствие из закона Планка, сделанное Бозе, можно сегодня увидеть в учебниках по статистической физике, и оно целиком и полностью соответствует квантовой теории.

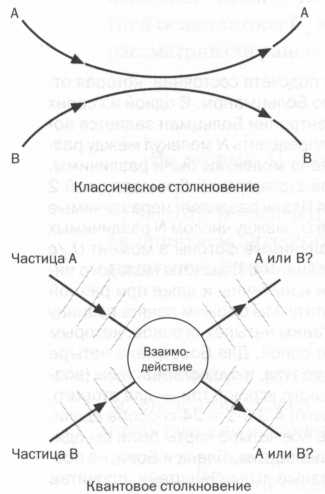
После квантового столкновения остаются две частицы, но мы не можем их отличить.