11.4. Геометрия Вселенной

Для наблюдений нам доступна лишь конечная область – часть большой Вселенной. Астрономические данные свидетельствуют в пользу того, что наблюдаемая часть пространства в больших масштабах однородна и изотропна. Это является основой наших представлений о геометрии Вселенной. При этом все выводы о параметрах большой Вселенной являются экстраполяцией.

Вселенная может быть конечной или бесконечной (ее объем может быть конечным или бесконечным), при этом конечность Вселенной не подразумевает наличия какой-либо границы. Современное понимание этой ситуации восходит к работам Бернхарда Римана (Georg Friedrich Bernhard Riemann), который впервые описал конечное, но безграничное пространство положительной кривизны. В любом случае у нас нет однозначных данных в пользу какой-то из этих двух альтернатив.

Наша Вселенная выглядит однородной, изотропной и плоской.

Геометрия Вселенной характеризуется еще несколькими параметрами. Изучать топологию (форму) Вселенной довольно сложно, поскольку нам доступна для наблюдений лишь малая ее часть. А вот кривизна пространства Вселенной – гораздо более перспективный предмет исследований.

Мы не видим никаких свидетельств в пользу конечности Вселенной или ее нетривиальной топологии.

Пространство может иметь положительную кривизну, нулевую (плоское пространство) и отрицательную. В пространстве положительной кривизны через точку, не лежащую на данной прямой, нельзя провести ни одной прямой, не пересекающейся с данной (вспомните, как сходятся меридианы на сфере), а суммы углов треугольников (на космологических масштабах) будут больше 180°. В пространстве нулевой кривизны (евклидова геометрия) через точку вне прямой можно провести только одну прямую, не пересекающуюся с данной, и сумма углов треугольника равна 180°. В пространстве отрицательной кривизны (геометрия Лобачевского) мы можем провести через точку сколько угодно прямых, которые никогда не пересекутся с данной, а сумма углов большого треугольника будет меньше 180°. В космологии эти три случая можно связать с величиной средней плотности Вселенной, плоскому пространству соответствует определенная критическая плотность.

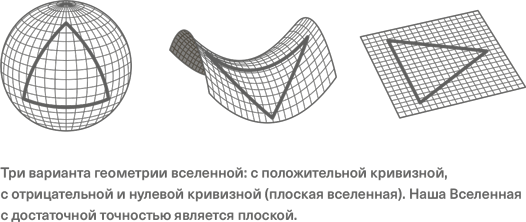
Наилучшие на сегодняшний день измерения геометрии Вселенной проведены с помощью наблюдения реликтового излучения (см. главу 12 «Реликтовое излучение»). Из этих наблюдений можно с высокой точностью определить отношение размера «звукового горизонта» (горизонта для распространяющихся колебаний в среде) на момент последнего рассеяния к расстоянию до источника реликтовых фотонов на момент их излучения, плюс нам известно значение красного смещения, соответствующее эпохе рекомбинации (z = 1100). Во вселенных разной кривизны линейный размер, соответствующий звуковому горизонту на z = 1100, имел бы на небесной сфере разные угловые масштабы. Данные показали, что в пределах ошибок (с точностью лучше процента) геометрия Вселенной – плоская. Конечно, наша Вселенная трехмерна, и, говоря о том, что она «плоская», мы имеем в виду применимость евклидовой геометрии для Вселенной в большом масштабе.

Наилучшие данные по кривизне и топологии Вселенной получены по наблюдениям реликтового фона.

Вселенная может обладать интересной и потенциально обнаружимой нетривиальной топологией. Причем это возможно для вселенной с любой кривизной: вспомните, что плоский лист бумаги можно свернуть в цилиндр, а можно сделать лист Мебиуса. Трехмерная вселенная может иметь сложную топологию, даже оставаясь плоской. Скажем, одна из возможностей состоит в том, что при небольшом размере вселенной за время ее существования свет мог обогнуть ее и мы видели бы копии («призраки» или «духи») далеких объектов или структур. Другая возможность связана с тем, что топология вселенной могла повлиять на анизотропию реликтового излучения. Поиск подобных особенностей проводился по каталогам квазаров, по картам реликтового излучения и другими методами. Однако ничего достоверного обнаружено не было.

Поэтому в настоящее время мы можем сказать, что наша Вселенная на космологических масштабах с высокой точностью:

• плоская;

• однородная;

• изотропная;

• имеет значительно большие размеры, чем потенциально доступная нам для наблюдений область.