Уменьшение нормы разрешённого багажа

Мой персональный поиск этой теории начинается с радикального рассуждения о том, на что она имеет право быть похожей. Если мы признаём, что реальность существует независимо от людей, то чтобы её описание было полным, оно должно также быть корректно определённым для нечеловеческих существ — скажем, инопланетян или суперкомпьютеров, — которые не знакомы с человеческими понятиями. Иначе говоря, такое описание должно выражаться в форме, лишённой всякого человеческого «багажа» вроде понятий «частица», «наблюдение» и других слов естественного языка.

При этом все физические теории, которым меня учили, содержат две компоненты: математические уравнения и «багаж» — слова, объясняющие, как эти уравнения связаны с тем, что мы наблюдаем и интуитивно понимаем. Выводя из теории следствия, мы придумываем для них новые понятия и слова, например протоны, атомы, молекулы, клетки, звёзды, поскольку ими удобно пользоваться. Важно помнить, однако, что эти понятия придуманы людьми. В принципе, всё может быть вычислено без «багажа». Гипотетический идеальный суперкомпьютер способен вычислить, как состояние Вселенной изменяется во времени, без «человеческой» интерпретации, просто рассчитывая, как будут двигаться все частицы или как будет изменяться волновая функция.

Предположим, что траектория баскетбольного мяча на рис. 10.2 — это один из тех блестящих бросков, которые приносят победу в самый момент звучания финальной сирены, и после игры вы хотите описать другу, как это было. Поскольку мяч состоит из элементарных частиц (кварков и электронов), вы можете описать его движения без всяких упоминаний о баскетбольном мяче:

• Частица № 1 движется по параболе.

• Частица № 2 движется по параболе.

• …

• Частица № 138 314 159 265 358 979 323 846 264 движется по параболе.

Это, однако, неудобно, поскольку время, которое понадобится для произнесения всего этого, превосходит возраст самой Вселенной. Это может быть и избыточно, поскольку все частицы получают толчок вместе и движутся как единое целое. Вот почему люди изобрели слово «мяч»: чтобы ссылаться на эту сущность и экономить время, описывая её движение как целого. Мяч изготовили люди, но дело обстоит подобным же образом и в случае составных объектов естественного происхождения — молекул, камней, звёзд и т. д.: придумывать для них слова удобно и ради экономии времени, и в качестве так называемых сокращающих абстракций, делающих понимание мира проще. Но при всей их полезности такие слова являются необязательным «багажом»: например, я неоднократно использовал в этой книге слово «звезда», однако вы можете в принципе заменить его определением звезды через её составляющие, скажем таким: «гравитационно связанный сгусток около 10⁵⁷ атомов, часть которых вступает в термоядерные реакции». Иными словами, в природе есть множество сущностей, которым так и тянет дать название. Наверняка почти каждое человеческое сообщество имеет в языке слово для обозначения звезды, часто придуманное независимо и отражающее местные культурные и лингвистические традиции. Предполагаю, что и большинство внеземных цивилизаций в далёких планетных системах также изобрело название или символ для звезды, даже если они не пользуются для коммуникации звуками.

Другой замечательный факт: нередко можно математически предсказать существование таких заслуживающих имени сущностей, опираясь на уравнения, управляющие их частями. На этом пути можно предсказать всю «легоподобную» иерархию структур (гл. 7), от элементарных частиц до атомов с молекулами, а также все объекты на каждом уровне, которым люди дали запоминающиеся имена. Например, если вы решаете уравнение Шрёдингера для пяти или менее кварков, то оказывается, что есть лишь два способа, которыми они могут быть достаточно стабильно организованы: либо как сгустки из двух верхних кварков и одного нижнего, либо как сгустки из двух нижних кварков и одного верхнего. Люди ради удобства добавили в свой «багаж» названия для сгустков этих двух типов: протоны и нейтроны. Аналогично, если применить уравнение Шрёдингера к таким сгусткам, оказывается, что существует лишь 257 способов, которыми они могут быть устойчиво объединены друг с другом. Мы добавили в «багаж» название для этих протон-нейтронных ансамблей — атомные ядра, и придумали названия для каждого их типа: водород, гелий и т. д. Уравнение Шрёдингера также позволяет вычислить все способы соединения атомов в более крупные объекты, но на этот раз стабильных объектов оказывается настолько много, что всем им давать имена неудобно. Поэтому мы именуем только важные классы таких объектов (молекулы, кристаллы и т. д.) и наиболее распространённые или интересные объекты в каждом классе (вода, графит, алмаз).

Я рассматриваю такие составные объекты как эмерджентные в том смысле, что они возникают как решения уравнений, описывающих более фундаментальные объекты. Их эмерджентность — трудноуловимое свойство, поскольку исторически научный прогресс по большей части шёл в противоположном направлении. Так, люди узнали о звёздах прежде, чем поняли, что они состоят из атомов; узнали об атомах прежде, чем поняли, что они состоят из электронов, протонов и нейтронов; узнали о нейтронах прежде, чем открыли кварки. Для каждого эмерджентного объекта, который для нас важен, люди собрали «багаж» в форме новых понятий.

Того же характера эмерджентность и накопление человеческого «багажа» видны на рис. 10.5. Я привожу грубую схему организации научных теорий в генеалогическое древо, в котором каждая теория может быть выведена (по крайней мере в принципе) из более фундаментальных. Все эти теории имеют две составляющие: математические уравнения, а также слова, которые объясняют, как уравнения связаны с тем, что мы наблюдаем. Например, квантовая механика, как её обычно излагают в учебниках, содержит обе компоненты (гл. 8): математическую, такую как уравнение Шрёдингера, и записанные на естественном языке фундаментальные постулаты вроде утверждения о коллапсе волновой функции. На каждом уровне иерархии теорий вводятся новые понятия (протоны, атомы, клетки, организмы, культуры и т. д.), потому что они удобны и охватывают суть того, что происходит, без обращения к вышестоящей, более фундаментальной теории. Все эти понятия вводят люди: в принципе, всё может быть выведено из фундаментальной теории на вершине древа, хотя такой крайний редукционизм на практике обычно бесполезен. Грубо говоря, по мере движения вниз по древу количество слов увеличивается, а уравнений — уменьшается, едва не достигая нуля в таких предельно прикладных сферах, как медицина или социология. Напротив, теории, близкие к вершине, сильно математизированы, и физики с трудом описывают понятия в доступном обывателю виде, если это вообще возможно.

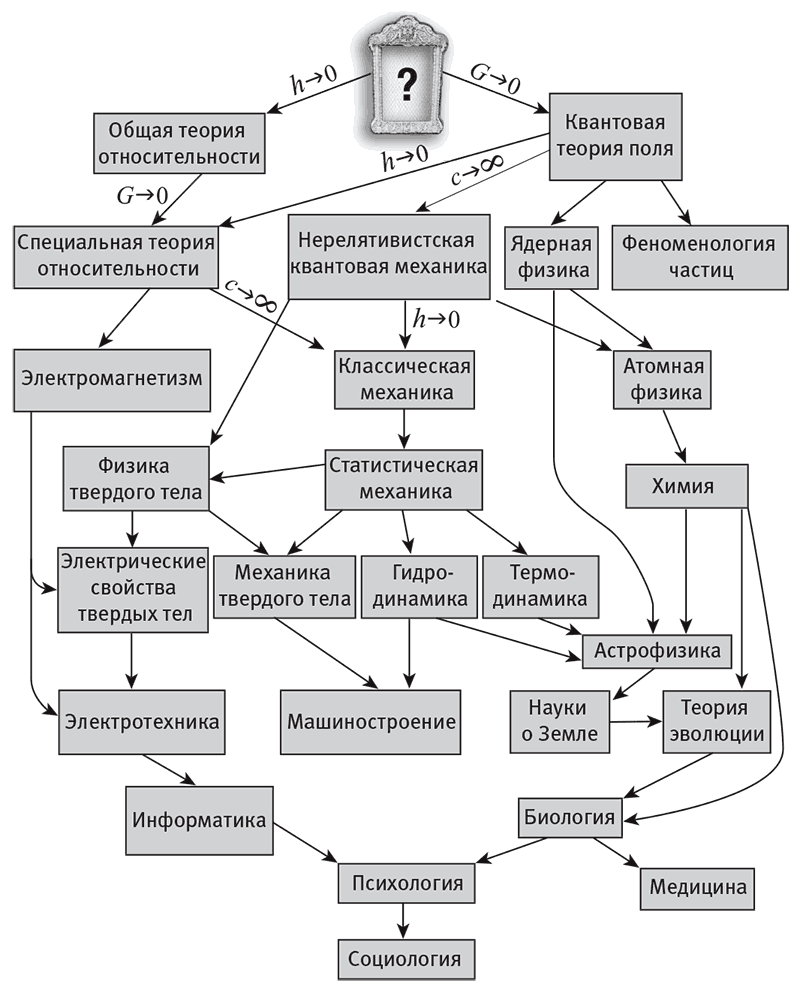
Рис. 10.5. Теории можно выстроить в «фамильное древо», где каждая из них может быть выведена, по крайней мере в принципе, из более фундаментальных. Например, специальную теорию относительности можно получить из общей теории относительности в приближении, при котором ньютоновская гравитационная постоянная G равна нулю. Классическая механика выводится из специальной теории относительности в приближении бесконечности скорости света c. Гидродинамика со всеми её понятиями, например плотностью и давлением, вытекает из классической физики столкновений частиц. Однако случаев, когда переходы по стрелкам хорошо понятны, меньшинство. Вывод биологии из химии или психологии из биологии на практике кажется недостижимым. Лишь отдельные, приближённые аспекты таких дисциплин математизированы, и, вероятно, все математические модели, имеющиеся сейчас в физике, также являются аппроксимациями отдельных аспектов реальности.

Высшая цель физики — найти то, что в шутку называют теорией всего (ТВ), из которой может быть выведено всё остальное. Ей предстоит занять место большого вопросительного знака наверху древа теорий. Здесь чего-то недостаёт (гл. 7): у нас нет целостной теории, объединяющей гравитацию и квантовую механику. ТВ стала бы полным описанием внешней физической реальности, существование которой предполагается в гипотезе внешней реальности. Выше я показал, что полное описание должно быть свободно от любого «багажа», то есть не должно содержать никаких понятий. Иными словами, оно должно быть чисто математической теорией без объяснений или «постулатов», как в учебниках по квантовой механике (математики прекрасно справляются — и часто этим гордятся — с изучением абстрактных математических структур, которые не имеют никакого внутреннего смысла или связи с физическими понятиями). Так что бесконечно разумный математик должен быть способен вывести всё древо теорий на рис. 10.5 лишь из этих уравнений, извлекая из них свойства физической реальности, которую они описывают, свойства её обитателей, их восприятие мира и даже слова, которые они придумывают. Эта чисто математическая «теория всего» потенциально может оказаться достаточно простой для описания с помощью уравнений, которые уместятся на футболке.

Всё это неуклонно ведёт нас к вопросу: действительно ли можно найти такое описание внешней реальности, в котором не было бы никакого «багажа»? Если да, то описание объектов нашей внешней реальности и взаимосвязей между ними было бы совершенно абстрактным, а любые слова или символы стали бы не более чем метками без какого-либо априорно подразумеваемого смысла. Свойства же всех таких сущностей исчерпывались бы их связями между собой.

Математические структуры

Для ответа на этот вопрос необходимо присмотреться к математике. Для современного логика математическая структура — это в точности следующее: набор абстрактных сущностей с отношениями между ними. Возьмём, например, целые числа или геометрические объекты, вроде любимого пифагорейцами додекаэдра. Это совершенно не похоже на первоначальное восприятие математики большинством из нас — как садистской формы наказания или набора трюков для манипулирования числами. Математика, развиваясь, стала, подобно физике, задаваться более широкими вопросами.

Современная математика — это формальное исследование структур, которые можно определить чисто абстрактным способом, без человеческого «багажа». Считайте математические символы просто метками без внутреннего содержания. Неважно, пишете ли вы «два плюс два равно четыре», 2 + 2 = 4 или dos m?s dos es igual a cuatro. Обозначения, используемые для указания сущностей и их взаимосвязей, не имеют значения; целые числа обладают лишь теми свойствами, которые связывают их между собой. То есть мы не изобретаем математические структуры: мы открываем их, а изобретаем лишь обозначения для их описания. Если другая цивилизация заинтересуется трёхмерными фигурами, состоящими лишь из одинаковых плоских граней, она может открыть пять форм, представленных на рис. 7.2, которые мы, земляне, называем платоновыми телами. Инопланетяне могут придумать для них собственные названия, но не смогут изобрести шестую фигуру — её просто не существует.

Итак, два основных вывода:

1. Из гипотезы внешней реальности вытекает, что «теория всего» (полное описание нашей внешней физической реальности) не содержит «багажа».

2. Нечто, имеющее описание, совершенно свободное от «багажа», — это не что иное, как математическая структура.

Из этих тезисов, взятых вместе, вытекает гипотеза математической Вселенной, то есть утверждение о том, что внешняя физическая реальность, описываемая посредством «теории всего», является математической структурой.[67] Итак, если вы верите во внешнюю реальность, независимую от людей, то вы должны поверить и в то, что наша физическая реальность является математической структурой. Ничто больше не имеет свободного от «багажа» описания. Иными словами, мы живём в гигантском математическом объекте — гораздо более сложном, чем додекаэдр, и, вероятно, даже гораздо более сложном, чем объекты с пугающими названиями вроде многообразий Калаби — Яу, тензорных расслоений или гильбертовых пространств, которые появляются в передовых современных физических теориях. Всё в нашем мире чисто математическое — включая нас самих.