Проверка мультиверса IV уровня

Мы показали, что из гипотезы внешней реальности (ГВР) — она утверждает, что внешняя реальность существует совершенно независимо от людей, — вытекает гипотеза математической Вселенной (ГМВ): наша внешняя физическая реальность является математической структурой, а из неё, в свою очередь, следует существование мультиверса IV уровня. Поэтому наиболее прямой способ усилить или ослабить нашу уверенность в мультиверсе IV уровня — это продолжить изучение ГВР. Хотя однозначности относительно ГВР по-прежнему нет, я думаю, справедливо сказать, что большинство моих коллег-физиков под ней подпишется. А недавние успехи стандартных моделей в физике элементарных частиц и космологии оставляют мало места для предположений, будто наша фундаментальная физическая реальность, какой бы она ни была, не может существовать без нас. Рассмотрим тем не менее два потенциальных способа прямой проверки ГМВ и мультиверса IV уровня.

Предсказание типичности

Открытие того, что физические параметры кажутся точно настроенными для жизни (гл. 6), можно интерпретировать как свидетельство в пользу мультиверса, где все параметры принимают значения в широком диапазоне. Эта интерпретация делает существование обитаемой вселенной вроде нашей неудивительным и предсказывает, что именно в ней мы и должны себя обнаружить. В частности, мы видели, что одно из самых сильных свидетельств в пользу мультиверса II уровня появилось из наблюдаемой точной настройки плотности тёмной энергии. Может ли, хотя бы в принципе, точная настройка свидетельствовать и в пользу IV уровня мультиверса?

В 2005 году на физической конференции в Кембридже, прогуливаясь поздно вечером по старинным дворам Тринити-колледжа и беседуя с Энтони Агирре, я вдруг понял, что ответ — «да». И вот почему.

Допустим, подруга привезла вас в незнакомый город. Вы выходите из машины и видите странный набор дорожных знаков (рис. 12.9), запрещающих парковаться везде, за исключением места, где припарковалась она. Оказывается, в рамках экологической кампании новый мэр заказал десять знаков, которые случайным образом расставили на улице. Каждый знак запрещает парковку вдоль всей улицы с левой или с правой стороны от знака. Проделав кое-какие вычисления, вы понимаете, что такой случайный процесс будет обычно запрещать парковку на всей улице и лишь с вероятностью около 1 % останется место, где парковаться разрешено.[88] Это случится, только если все знаки со стрелками влево будут помещены левее всех знаков со стрелками вправо.

Просто совпадение? Если вы, подобно типичному учёному, не терпите необъяснимых совпадений, вы склонитесь к интерпретации, которая не требует такой невероятной удачи: в этом странном городе существует много улиц, возможно, около ста или больше. Это сделает вероятным существование легальной парковки на некоторой улице, и поскольку ваша подруга знает город, совершенно неудивительно, что она выбрала для парковки именно это место. Данный пример точной настройки отличается от рассмотренного в гл. 6: то, что кажется точно настроенным, является не непрерывным, как плотность тёмной энергии, а скорее дискретным: все направления стрелок, указывающих влево и вправо, определённым образом согласованы.

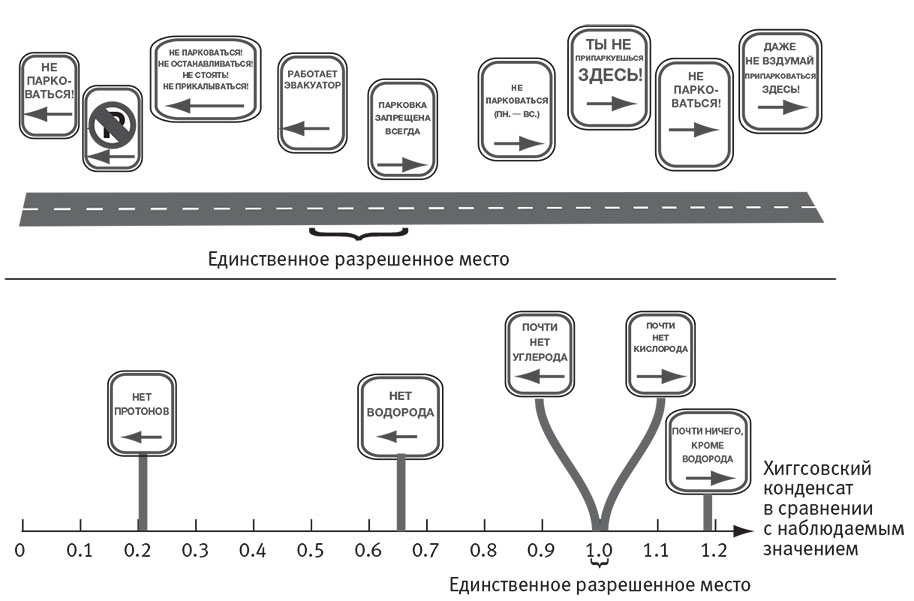
Рис. 12.9. Если на улице случайным образом размещено множество знаков и каждый запрещает парковку на всей улице либо слева, либо справа от знака, то крайне маловероятно, чтобы парковка на улице была разрешена хоть где-нибудь. Это произойдёт, лишь если все стрелки влево располагаются слева от всех стрелок вправо (вверху). Аналогично, если у вселенной есть физический параметр, который должен удовлетворять множеству ограничений, чтобы позволить существование жизни (внизу), априори маловероятно, чтобы существовал хоть какой-нибудь пригодный для жизни диапазон значений этого параметра. Ситуации вроде тех, что показаны на рисунках, могут, таким образом, интерпретироваться как свидетельство существования соответственно множества улиц или математических структур в мультиверсе IV уровня.

Мой пример с парковкой, конечно, дурацкий, но, как показано в нижней части рис. 12.9, в нашей Вселенной мы наблюдаем нечто похожее. По горизонтальной оси отложен параметр, связанный с недавно открытой частицей Хиггса. А в недавней работе Джона Донахью, Крейга Хогана, Хайнца Оберхаммера и их соавторов показано, что эта величина, подобно плотности тёмной энергии, кажется очень точно настроенной: она примерно на 16 порядков меньше, чем было бы естественно ожидать. При этом изменение даже на 1 % вверх или вниз значительно изменяет количество кислорода и производимого звёздами углерода. Увеличение на 18 % радикально снижает способность водорода к ядерным реакциям, в результате которых в звёздах рождались бы хоть какие-нибудь другие атомы, тогда как уменьшение на 34 % приводит к распаду атомов водорода, поскольку протоны проглатывают свои электроны и превращаются в нейтроны. При пятикратном уменьшении этой величины даже одиночные протоны распадаются на нейтроны. Тогда во Вселенной вообще не будет атомов.

Как это интерпретировать? Прежде всего это кажется дополнительным подтверждением существования мультиверса II уровня, в котором варьируют физические параметры. Точно так же, как мультиверс объясняет, почему мы обнаружили плотность тёмной энергии, как раз подходящую для образования галактик, он может объяснить и то, почему обнаруженные свойства поля Хиггса очень подходят для существования более сложных атомов, чем водород. И неудивительно, что мы в одной из тех сравнительно редких вселенных, где существуют и интересные атомы, и интересные галактики, раз уж жизнь требует по крайней мере минимального уровня сложности.

Но возникает вопрос: почему стрелки на нижней схеме согласованы так, что создают хоть какой-нибудь пригодный для жизни диапазон значений в свойствах поля Хиггса? Это, конечно, может быть случайностью: пять произвольно расположенных стрелок образовали бы такой диапазон с вероятностью 19 %, так что нам понадобилась бы лишь небольшая удача. Более того, в силу особенностей ядерной физики эти пять стрелок не являются независимыми, так что я не рассматриваю пример с пятью стрелками в качестве сильного аргумента в пользу чего бы то ни было. Однако вполне вероятно, что дальнейшие физические исследования могут открыть более впечатляющую точную настройку этого дискретного типа, скажем, с десятью или более стрелками, согласованными так, чтобы получался пригодный для существования жизни диапазон значений некоторого физического параметра или параметров.[89] Если это случится, мы сможем рассуждать, как и в ситуации, представленной в верхней части рисунка: что это является свидетельством существования не только других улиц, но и других вселенных, где иные законы физики порождают совершенно иные требования для жизни! В некоторых случаях эти вселенные могут существовать в мультиверсе II уровня, в областях, где те же фундаментальные законы физики порождают иное фазовое состояние пространства с иными эффективными законами. В других случаях, однако, можно сказать, что подобное нереализуемо и другие вселенные должны подчиняться иным фундаментальным законам, что соответствует иным математическим структурам в мультиверсе IV уровня. Иными словами, сейчас мы не имеем прямых наблюдательных подтверждений существования мультиверса IV уровня, однако в будущем мы можем получить их.

Предсказание математических закономерностей

В эссе 1960 года Вигнер утверждал, что «невероятная эффективность математики в естественных науках есть нечто граничащее с мистикой» и что «никакого рационального объяснения этому факту нет». Гипотеза математической Вселенной (ГМВ) предлагает такое объяснение. Она объясняет полезность математики для описания физических законов как естественное следствие того факта, что последние являются математическими структурами и мы просто открываем их шаг за шагом. Различные приближения, из которых складываются наши современные физические теории, успешны потому, что простые математические структуры обеспечивают хорошие аппроксимации для отдельных аспектов более сложных математических структур. Иными словами, наши успешные теории являются не математическими аппроксимациями физики, а математическими аппроксимациями математики.

Одно из ключевых проверяемых предсказаний гипотезы математической Вселенной таково: физики и далее будут находить в природе математические закономерности. Поль Дирак в 1931 году так выразил предсказательную силу идеи математической Вселенной: «Наиболее мощный способ продвижения, который можно предложить сейчас, состоит, пожалуй, в том, чтобы использовать все ресурсы чистой математики в попытках завершать и обобщать математический формализм, образующий соответствующую основу теоретической физики, и после каждого успеха в этом направлении пытаться интерпретировать новые математические явления в терминах физических реальностей».[90]

Насколько успешным до сих пор было это предсказание? Спустя два тысячелетия после того, как пифагорейцы выдвинули идею математической Вселенной, новые открытия позволили Галилею охарактеризовать природу как книгу, написанную на языке математики. Затем были открыты гораздо более глубокие математические закономерности, от движения планет до свойств атомов. Стандартные модели в физике элементарных частиц и космологии открыли новый «непостижимый» математический порядок, охватывающий впечатляющий диапазон: от микрокосма элементарных частиц до макрокосма ранней Вселенной — возможно, позволяющий успешно вывести все когда-либо выполненные физические измерения для определения набора из 32 чисел (табл. 10.1). Не знаю другого убедительного объяснения этой тенденции, кроме следующего: физический мир целиком является математическим.

Я вижу здесь два исхода. Если я ошибаюсь и ГМВ ложна, то физика в конце концов наткнётся на непреодолимое препятствие, из-за которого прогресс станет невозможен: не останется новых математических закономерностей, которые можно было бы открыть, несмотря на то, что мы всё ещё не будем располагать полным описанием нашей физической реальности. Например, убедительная демонстрация того, что в законах природы существует фундаментальная случайность (в противоположность детерминистическому клонированию наблюдателя, который субъективно ощущает случайность), позволила бы отвергнуть ГМВ. С другой стороны, если я прав, то наши поиски понимания реальности не встретят никаких пределов и мы будем ограничены только нашим воображением.