Что не так с Большим взрывом?

Но эта премия — не единственное достижение Алана. Около 1980 года он узнал от физика Боба Дикке, что во фридмановской модели Большого взрыва существуют серьёзные проблемы с самыми ранними стадиями, и предложил радикальное решение, которое назвал инфляцией.[16] Экстраполяция фридмановских уравнений расширяющейся Вселенной назад во времени приводит к огромным успехам: они отлично объясняют, почему далёкие галактики разбегаются от нас, и откуда взялся фон космического микроволнового излучения, и как возникли лёгкие элементы и многие другие наблюдаемые явления.

Вернёмся в прошлое, к границе нашего знания, к тому мгновению, когда Вселенная расширялась столь быстро, что в следующую секунду её размеры удвоились. Уравнения Фридмана говорят нам, что до того Вселенная была ещё плотнее и горячее, и этому нет предела. И, в частности, примерно на 1/3 секунды ранее имело место начало, когда плотность нашей Вселенной была бесконечной и всё существующее разлеталось друг от друга с бесконечной скоростью.

Вслед за Дикке Алан Гут тщательно изучил эту историю возникновения нашего мира и понял, что она страшно неестественна. Например, на четыре вопроса из числа приведённых в начале гл. 2 она даёт такие ответы:

– Что стало причиной нашего Большого взрыва?

— Объяснения этому нет. Уравнения просто учитывают, что это случилось.

– Произошёл ли наш Большой взрыв в одной точке?

— Нет.

– Где именно в пространстве произошёл наш Большой взрыв?

— Он случился везде, сразу в бесконечном множестве точек.

– Как бесконечное пространство может быть порождено за конечное время?

— Объяснения этому нет. Уравнения просто учитывают, что пространство было бесконечным уже в момент его появления.

Можно ли сказать, что эти ответы раскрывают суть дела и элегантно снимают все вопросы о Большом взрыве? Если нет, то вы в хорошей компании! На самом деле есть ещё много вещей, которые фридмановская модель Большого взрыва не может объяснить.

Проблема горизонта

Проанализируем тщательнее третий вопрос из списка. На рис. 5.2 проиллюстрирован тот факт, что температура излучения космического микроволнового фона почти одинакова (с точностью до пятой значащей цифры) во всех направлениях. Если бы Большой взрыв случился в одних областях пространства существенно раньше, чем в других, у этих областей было бы разное время для расширения и остывания и температура на наших картах космического микроволнового фона варьировалась бы от места к месту не на 0,002 %, а почти на 100 %.

Но не мог ли некий физический процесс привести к выравниванию температуры гораздо позднее Большого взрыва? В конце концов, если лить холодное молоко в горячий кофе, не удивительно, что когда вы начнёте пить, они станут однородно тёплыми. Проблема в том, что процесс смешивания требует времени: необходимо подождать, чтобы молекулы молока и кофе перемешались. Однако у отдалённых частей Вселенной, доступных нашим наблюдениям, не было времени для такого перемешивания (ещё в 60-х годах на это обратили внимание Чарлз Мизнер и его коллеги). У областей а и б (рис. 5.2), которые мы видим в противоположных направлениях на небе, не было времени для взаимодействия: даже информация, передающаяся со скоростью света, не успела бы дойти из а в б, поскольку свет от а прошёл полпути — до точки, где находимся мы. Это значит, что фридмановская модель Большого взрыва не даёт объяснения одинаковой температуры в точках а и б. Получается, что у этих областей было равное время для остывания после Большого взрыва, а отсюда следует, что они независимо испытали Большой взрыв почти в одно и то же время без какой-либо общей причины.

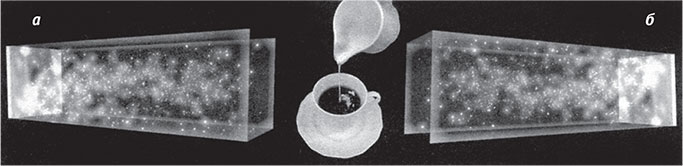
Рис. 5.2. У молекул горячего кофе и холодного молока достаточно времени для взаимодействия и выравнивания температуры. У плазмы в областях а и б не было времени для взаимодействия: даже информация, передаваемая со скоростью света, не успела бы дойти от а до б, поскольку свет от а достиг пока лишь тех, кто пьёт кофе на полпути к б. Поэтому с точки зрения фридмановской модели Большого взрыва тот факт, что плазма в областях а и б тем не менее обладает одинаковой температурой, является загадкой.

Чтобы лучше понять, какое недоумение это вызвало у Алана Гута, представьте вот что. Проверив электронную почту, вы обнаружили приглашение на ланч от приятеля, а затем увидели, что все остальные ваши приятели прислали вам по письму с приглашением на ланч и что все до единого письма отправлены одновременно. Вы, вероятно, решили бы, что имеет место сговор и что появление всех этих писем вызвано общей причиной. Возможно, друзья решили устроить вам вечеринку-сюрприз. Для завершения аналогии с загадкой Алана о Большом взрыве, где области а, б, … соответствуют вашим приятелям, добавим, что вам точно известно: ваши друзья никогда не встречались, не связывались друг с другом и не имели доступа к какой-либо общей информации до отправки вам приглашений. Тогда пришлось бы признать это невероятным совпадением. На самом деле, слишком невероятным, так что вы, вероятно, решили бы, что сделали некорректное допущение и ваши друзья всё же смогли снестись. И это точно тот вывод, который сделал Алан: то, что бесконечное множество независимых областей пространства испытали Большой взрыв одновременно, не может быть беспричинным совпадением. Должен иметься некий физический механизм, вызывающий и взрыв, и синхронизацию. Один необъяснённый Большой взрыв — это уже плохо; бесконечное число необъяснённых Больших взрывов, вдобавок прекрасно синхронизированных, — уже ни в какие ворота не лезет.

Это проблема горизонта: она затрагивает то, что мы видим на своём космологическом горизонте — в самых отдалённых областях, доступных для наблюдения. Словно этого мало, Боб Дикке рассказал Алану о втором затруднении фридмановской теории Большого взрыва, которую он назвал проблемой плоской геометрии.

Проблема плоской геометрии

Измерения показывают, что наше пространство с высокой степенью точности плоское. Дикке считал, что это странно — если верна фридмановская модель Большого взрыва: такое состояние крайне неустойчиво, и нет оснований ожидать, что оно сохранится надолго. Например, в гл. 3 мы обсуждали неустойчивость остановившегося велосипеда, связанную с тем, что малейшее его отклонение от идеального равновесия усиливается гравитацией, так что вы сильно удивитесь, увидев ничем не поддерживаемый велосипед, который простоит вертикально несколько минут. На рис. 5.3 показаны три решения уравнений Фридмана, иллюстрирующих космологическую неустойчивость. Средняя кривая соответствует плоской Вселенной, которая остаётся идеально плоской и расширяется вечно. Две другие кривые начинаются почти так же, с практически неискривлённого пространства через миллиардную долю секунды, и спустя миллиардную долю секунды их плотности различаются лишь в 24-й значащей цифре.[17] Но гравитация усиливает эти ничтожные различия, и в следующие 500 млн лет это заставляет Вселенную, описываемую нижней кривой, прекратить расширение и коллапсировать в Большом хлопке — Большом взрыве наоборот. В этой коллапсирующей в итоге Вселенной пространство приобретает такое искривление, что сумма углов треугольника оказывается гораздо больше 180°. Верхняя кривая, напротив, описывает Вселенную, искривлённую таким образом, что углы в сумме дают меньше 180°. Она расширяется гораздо быстрее пограничной плоской Вселенной, и к настоящему времени её газ должен был стать слишком разрежённым, чтобы образовывать галактики, а соответствующий сценарий можно назвать «Большим замерзанием».

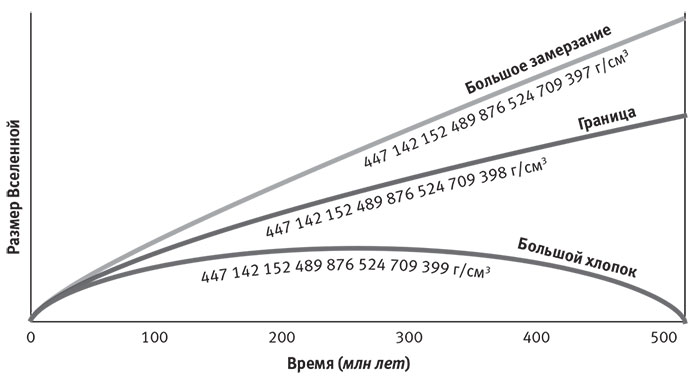
Рис. 5.3. Ещё одна необъяснённая загадка фридмановской модели Большого взрыва состоит в том, что Вселенная так долго существует без заметного искривления пространства, ведущего к Большому хлопку или Большому замерзанию. Эти кривые соответствуют незначительно различающимся значениям плотности в момент, когда возраст Вселенной составлял одну миллиардную секунды: изменение последней из 24 цифр приводит к переходу в режим Большого хлопка или Большого замерзания прежде, чем Вселенная достигнет 4 % своего нынешнего возраста. (Благодарю Неда Райта за идею рисунка.)

Так почему наша Вселенная плоская? Если заменить 24 цифры на рис. 5.3 случайными значениями и решить уравнение Фридмана, то вероятность получить Вселенную, которая останется плоской спустя 14 млрд лет, будет меньше, чем для дротика, брошенного с Марса, попасть точно в центр мишени на Земле. Тем не менее фридмановская модель Большого взрыва не предполагает никакого объяснения этому совпадению.

Конечно, рассудил Алан Гут, должен существовать некий механизм, который вынуждает Вселенную иметь точно такую плотность, какая требуется, чтобы обеспечить исключительно плоскую геометрию в самом начале её истории.