Когда вы?

Итак, математическая структура может содержать наблюдательные мгновения (в них проявляется самосознание), подобные тому, что вы испытываете прямо сейчас. Выше мы описали трудности обнаружения этих наблюдательных мгновений и то, как они могут субъективно ощущаться. Вы существуете в математической структуре, содержащей определённого рода пространство-время, и чтобы делать физические предсказания, следует попытаться узнать: в какого рода математической структуре вы находитесь, каково местоположение в ней вашего текущего наблюдательного мгновения — то есть где в пространстве и когда во времени вы находитесь? Как мы увидим, часть, относящаяся к вопросу когда, ещё тоньше, чем связанная с вопросом где, особенно если число ваших копий меняется во времени.

За пределами попперовского двухвременья

Для меня наука — это всё, что касается понимания реальности и нашего места в ней. В прагматическом отношении это касается поиска модели реальности, позволяющей предсказывать будущее настолько успешно, насколько это возможно, чтобы мы могли предпринимать такие действия, которые, согласно нашим предсказаниям, дают наилучший результат (для облегчения этой задачи, кажется, мы и имели счастье приобрести сознание). Мыслители веками пытались формализовать этот научный процесс, и, думаю, большинство современных учёных согласится, что теперь мы имеем следующее:

1. Сделать предсказания на основе допущений.

2. Сравнить наблюдения с предсказаниями, пересмотреть допущения.

3. Повторить.

Совокупность предположений называют теорией. В контексте ГМВ ключевые предположения, которые составляют модель реальности, касаются того, какую математическую структуру мы населяем, и какое конкретно наблюдательное мгновение в ней является воспринимаемым вами прямо сейчас. Карл Поппер подчёркивал важность второго пункта списка, доказывая, что предположения, которые не дают проверяемых предсказаний, не являются научными. Хотя он упирал на фальсифицируемость (обязательно должна иметься принципиальная возможность проверить, не является ли научная теория ложной), существует красивый математический инструментарий, называемый байесовской теорией принятия решений, который обобщает дихотомию «истина — ложь», добавляя ей оттенки серого. Любому возможному предположению приписывается число от 0 до 1 — вероятность, с которой, как вы думаете, оно верно, и есть простая формула, позволяющая обновлять эти вероятности, когда вы делаете новые наблюдения.

Но при всей элегантности этого подхода и благожелательном к нему отношении есть проблема: он требует двух связанных наблюдательных мгновений. В первое мгновение вы делаете предсказание, а во второе оцениваете результат. Это годится в обычной ситуации, когда есть, была и всегда будет лишь одна ваша копия (рис. 11.8, слева). Однако всё не так в сценарии с параллельными вселенными, где у вас есть альтернативные «я». Это может приводить к новым эффектам (гл. 6, 8), например, к субъективному бессмертию и субъективной случайности (рис. 11.8).

В контексте ГМВ мы показали, что восприятие течения времени, а также выдвижение предположений и осуществление наблюдений имеют место в каждое единичное наблюдательное мгновение, которое мы переживаем. Это означает, что мы должны выйти за пределы попперовского двухвременного подхода к науке и предложить одновременной подход, применимый к единственному наблюдательному мгновению. Мне нравится мечтать о замечательном карманном пульте управления реальностью. Участвуя в скучных совещаниях, я могу нажать кнопку ускоренной перемотки вперёд. Когда я испытываю восторг, то могу «отмотать» время назад и пережить всё столько раз, сколько захочу. А чтобы превзойти Поппера, я просто нажимаю кнопку «Пауза». Теперь я поистине могу в духе Горация поймать мгновение, рассмотреть его в целостности, прочувствовать и отрефлексировать. В частности, я могу раздумывать над тем, что я предполагаю и что наблюдаю. Если мой мозг работает хорошо, я обнаружу, что моя внутренняя модель реальности отлично согласуется с последними новостями, которые мои чувства поставляют из внешнего мира. И если мой алгоритм научных рассуждений хорош, я обнаружу, что предсказания, которые, как я помню, делаются для этого мгновения, находятся в полном согласии с тем, что действительно происходит. Пока чувства интенсивно трудятся над регистрацией новой информации, которой предстоит быть сознательно воспринятой в будущие наблюдательные мгновения, сознательная часть моей психики занята применением алгоритма научных рассуждений для обновления набора допущений, касающихся более тонких и абстрактных аспектов реальности.

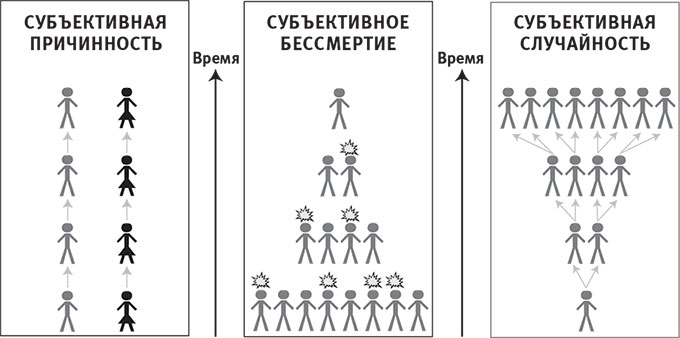
Рис. 11.8. Когда каждое наблюдательное мгновение можно однозначно связать с предшествующим и последующим, мы субъективно воспринимаем это как причинность (слева). Когда некоторые последователи исчезают, мы можем воспринимать это субъективно как бессмертие. Когда некоторые субъективно различимые последователи имеют одного и того же предшественника, мы субъективно воспринимаем это как случайность.

Почему вы не муравей?

Так как вы должны рассуждать в своё наблюдательное мгновение, нажав кнопку «Пауза»? Вам понадобится хорошая концептуальная схема, которая позволит не только уложить в неё мультиверс, но и справиться с аргументом Судного дня и иными философскими головоломками. Если вы признаёте гипотезу математической Вселенной, то должны попытаться представить, в какой математической структуре вы живёте. Если эта структура содержит множество наблюдательных мгновений, субъективно ощущаемых как ваши, то вы можете быть любым из них. Если в математике нет чего-либо, нарушающего симметрию и отдающего предпочтение одним мгновениям перед другими, вы с равной вероятностью выберете любое из них. Тем не менее, как я показал в статье о математической Вселенной в 1996 году, вы придёте к заключению:

Следует рассуждать, как если бы ваше наблюдательное мгновение было случайно выбрано из всех возможных.

Два последних десятилетия философы спорят о различных альтернативных способах рассуждения. Эта дискуссия спровоцирована отчасти аргументом Судного дня (который я кратко разберу) и связанными с ним головоломками. Основная идея — нам следует ожидать обнаружить своё сознание не в произвольном месте (как следует из принципа Коперника), а у случайного наблюдателя, имеющего долгую историю. Брэндон Картер сформулировал это как слабый антропный принцип (гл. 6), а Александр Виленкин — как принцип заурядности. Его исследовали Ник Бострём, Пол Олмонд, Милан Чиркович и другие современные философы. В 2002 году Бострём ввёл понятие, ставшее уже общепринятым — сильное допущение о самовыборке (СДСВ):

Каждое наблюдательное мгновение должно анализироваться так, как если бы оно было случайным образом выбрано из всех наблюдательных мгновений референтного класса.

Тонкость в том, как интерпретировать понятие референтный класс, и философы, признающие СДСВ, об этом спорят. Если использовать вариант с наиболее жёсткими опциями и ограничить референтный класс наблюдательными мгновениями ваших копий, которые субъективно неотличимы от ваших собственных наблюдательных мгновений, то мы вернёмся к моему старому подходу. Однако можно прийти к интересным выводам, используя гораздо более либеральный подход. Вы по-прежнему будете приходить к верным заключениям, даже если позволены различные наблюдательные мгновения, лишь бы способ, каким они субъективно ощущаются как различные, не влиял на ответ, который вы ищете. Рассмотрим пример СДСВ — задачу Бострёма о Спящей Красавице.

Претендентки на роль Спящей Красавицы соглашаются участвовать в следующем эксперименте, обо всех условиях которого им сообщают. В воскресенье участница опыта ложится спать. Затем подбрасывается монета с равными шансами упасть на одну из сторон. Если выпадает решка, Красавицу будят и задают ей вопрос только в понедельник. Если выпадает орёл, Красавицу будят и задают вопрос в понедельник и вторник, но когда она вновь ложится спать в понедельник, ей дают препарат, вызывающий амнезию, и это гарантирует, что она не сможет вспомнить предыдущее пробуждение. Всякий раз, когда Красавицу будят, её спрашивают: «Как бы вы оценили шансы, что выпала решка?»

После большого числа публикаций на эту тему философское сообщество разделилось на считающих, что она должна назвать 1/2, и тех, кто придерживается вероятности 1/3. В рамках ГМВ не существует истинной случайности, поэтому заменим монету квантовым измерением, которое в равной мере реализует оба исхода в параллельных двух вселенных III уровня. Теперь в математической структуре, которая соответствует Красавице в момент интервью, есть три субъективно неразличимых наблюдательных мгновения, и все они одинаково реальны:

1. Выпала решка, и это понедельник.

2. Выпал орёл, и это понедельник.

3. Выпал орёл, и это вторник.

Поскольку лишь один из трёх вариантов соответствует выпадению решки, Красавица должна приписать этому событию вероятность 1/3 и испытывать соответствующее субъективное чувство случайности, когда это обнаружит.

Теперь предположим, что экспериментаторы тайно решили перекрасить ей ногти в цвет, зависящий от исхода квантового измерения. Это означает, что не все наблюдательные мгновения являются неразличимыми, но, поскольку красавица не знает, как построен цветовой код, её оценка шансов не должна измениться. Иными словами, мы можем свободно расширять референтный класс, если только это не влияет на результаты.

У этого вывода есть радикальные следствия. Каким бы огромным и безумным ни был мультиверс, люди скорее всего довольно типичны среди наблюдателей, задающихся такого рода вопросами. Например, крайне маловероятно, чтобы типичная планетная система содержала квадриллионы похожих на нас гоминид, поскольку в таком случае у нас было бы примерно в миллион раз больше шансов обнаружить себя в такой густонаселённой планетной системе, а не в нашей собственной, с её жалкими 7 млрд жителей. СДСВ позволяет делать утверждения о том, что происходит даже в таких местах, которые мы не можем наблюдать.

Однако, как и любой мощный инструмент, СДСВ следует применять с осторожностью. Например, почему вы не муравей? Если в качестве референтного класса взять углеродные формы земной жизни, то наши шестиногие друзья, которых свыше десяти квадриллионов (10¹⁶), превзойдут по численности нас, двуногих, более чем в миллион раз. Не следует ли отсюда, что вашему текущему наблюдательному мгновению в миллион раз вероятнее оказаться муравьиным, чем человеческим? Если так, то ваша фундаментальная структура реальности была бы исключена с надёжностью 99,9999 %. Да, согласен, мы пренебрегли тем фактом, что люди живут примерно в 100 раз дольше муравьёв, но это не избавляет от тревожного вывода.

В действительности решение лежит в выборе референтного класса. Его можно выбрать многими способами (рис. 11.9): самый обширный класс будет включать все наблюдательные мгновения всех самосознающих субструктур, а самый узкий — лишь те, в которых субъективно ощущается точно то же, что ощущаете вы в данный момент. Если вы спрашиваете, какого рода сущностью вы скорее всего окажетесь, то ваш референтный класс, очевидно, должен быть сужен до сущностей, которые задают такие вопросы, и муравьи в него не попадут.

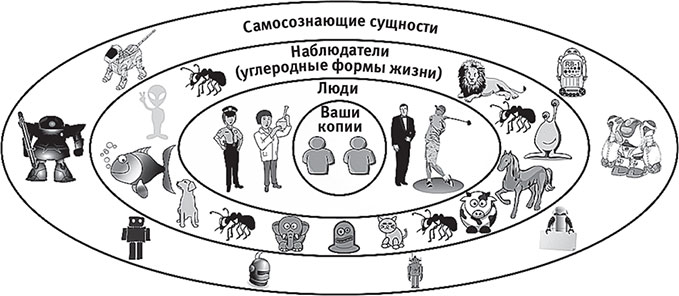
Рис. 11.9. «Какова вероятность того, что [подставьте свой любимый вопрос], при условии, что я…?» То, чем вы заполняете пропуск — это ваш референтный класс. В рамках гипотезы математической Вселенной всегда справедливо рассуждать так, как если бы вы были случайным членом наиболее узкого референтного класса, соответствующего всем наблюдательным мгновениям, которые субъективно воспринимаются так же, как ваши. Но в некоторых случаях вы можете получить дополнительные корректные и интересные выводы, расширяя свой референтный класс, скажем, до людей или других самосознающих сущностей, способных задать такой же вопрос.

Вопрос о выборе правильного референтного класса соответствует правильному применению того, что статистики называют условными вероятностями. Неумелая работа с ними может привести к провалу. Так, в 2010 году большой опрос не смог предсказать переизбрание в Неваде лидера сенатского большинства Гарри Рида, поскольку автоматизированная система телефонных опросов вешала трубку, когда абонент не говорил по-английски, и в результате не были учтены ответы поддерживающих Рида испаноязычных избирателей. В гл. 6 мы увидели, что типичная область пространства окажется скорее всего в такой вселенной, где тёмной энергии слишком много для того, чтобы образовались галактики, а типичный атом водорода в нашей Вселенной скорее всего окажется в составе межгалактического газового облака или в звезде. Но эти варианты не следует рассматривать как вероятные для вас самих: все точки и все атомы — это нерелевантные для вас классы, поскольку ни точки, ни атомы не задают вопросов.

Почему вы не больцмановский мозг?

Если вам кажется безумием возможность иметь внеземных одноклассников в своём референтном классе, вас может позабавить то, что некоторые мои коллеги спорят об ещё более экзотических одноклассниках: симуляциях и больцмановских мозгах.

Мы — живое доказательство того, что атомы можно соединить в сложную структуру, которая субъективно будет ощущать себя самосознающей. До сих пор физические исследования не дали свидетельств в пользу того, что наш пример является единственным возможным путём реализации сознания. Поэтому надо рассмотреть возможность существования других способов организации атомов, обладающих самосознанием, а также того, что некоторые жизненные формы (возможно, даже мы сами, или наши потомки) однажды породят такие сущности. Они могут напоминать разумных роботов, которые располагают телами, способными взаимодействовать с окружающим миром, или оказаться симуляциями, подобно персонажам с голопалубы в сериале «Звёздный путь: Следующее поколение» или агенту Смиту из «Матрицы»,[80] чьи тела являются виртуальными, а жизнь воспроизводится в виртуальной реальности чрезвычайно мощного компьютера. Подобные симуляции могут обладать наблюдательными мгновениями, которые субъективно ощущаются точно такими же, как ваши ощущения прямо сейчас.

В этом случае вам, очевидно, нужно включить в свой референтный класс смоделированных себя. Ник Бострём и другие учёные пришли к выводу: существует ненулевая вероятность того, что мы сами в действительности смоделированы. Я приведу контраргументы в следующей главе, но если вы хотите всё же действовать наверняка, в духе паскалевского пари, я советую жить полной жизнью и заниматься новыми интересными вещами. Тогда, если вы являетесь симуляцией, то, что вас породило, с меньшей вероятностью соскучится и выключит вас…

Теперь включим перемотку до современной Вселенной и рассмотрим её судьбу в долгосрочной перспективе. Ускоренное расширение заставит в конце концов рассеяться всю материю, которая сейчас заполняет нашу Вселенную. Но если плотность космической тёмной энергии остаётся постоянной (о чём говорят современные измерения), она всегда будет поставлять очень небольшое количество тепловой энергии. Это тепло возникает благодаря тем же квантовым флуктуациям, которые породили описанные в гл. 5 флуктуации космического микроволнового фона, и Стивен Хокинг сделал знаменитое открытие, состоящее в том, что чем быстрее расширяется Вселенная, тем выше хокинговская температура. Тёмная энергия заставляет нашу Вселенную расширяться гораздо медленнее, чем в период инфляции, так что температура, которую она обеспечивает, составляет около миллионной триллионной триллионной (10^–30) доли градуса выше абсолютного нуля.

Это не жарко даже по шведским стандартам, но всё же не абсолютный нуль, а значит, если ждать достаточно долго, тепловая энергия трансформирует себя во что угодно. В стандартной космологической модели это случайное трансформирование продолжается вечно, так что оно может спонтанно породить точную вашу копию, которая будет субъективно ощущать то же самое, что и вы, вместе со всеми ложными воспоминаниями обо всей вашей жизни. Но гораздо чаще будет воспроизводиться лишь ваш лишённый тела мозг, живущий достаточно долго, чтобы воспроизвести ваше текущее наблюдательное мгновение. И это будет происходить вновь и вновь, бесконечное число раз, так что для любой вашей копии, появившейся в результате развития и прожившей реальную жизнь, существует бесконечно много иллюзорных бестелесных мозгов, которые думают, что они прожили точно такую же реальную жизнь.

Это действительно серьёзное затруднение. Если наше пространство-время в самом деле содержит эти больцмановские мозги, то вы почти со стопроцентной надёжностью один из них! В конце концов наблюдательное мгновение вас, развившегося естественным путём, находится в том же референтном классе, что и мгновение тех мозгов, поскольку они субъективно ощущают то же самое, что и вы. Так что вам следует думать о себе как о произвольном наблюдателе этого мгновения, а среди них бестелесные в бесконечное число раз превосходят по численности обладающих телом…

Прежде чем вы слишком обеспокоитесь онтологическим статусом своего тела, вот простой тест, с помощью которого вы можете определить, являетесь ли вы больцмановским мозгом. Сделайте паузу. Загляните внутрь себя. Проанализируйте свои воспоминания. В сценарии с больцмановским мозгом в действительности более вероятно, что любое конкретное воспоминание является ложным. Однако для каждого набора ложных воспоминаний, которые могут казаться реальными, есть похожие наборы воспоминаний, в которые закралось несколько безумных битов (скажем, вы припоминаете Пятую симфонию Бетховена, звучащую совершенно статично). Они являются гораздо более вероятными, поскольку существует куда больше бестелесных мозгов с такими воспоминаниями. Это связано с тем, что существует гораздо больше способов сделать что-нибудь почти правильно, чем сделать это совершенно правильно. Значит, если вы действительно больцмановский мозг, который первоначально так о себе не думает, то как только вы начнёте рыться в памяти, вы должны обнаруживать всё больше нелепого. И после этого вы почувствуете, что ваша реальность растворяется по мере того, как частицы возвращаются в холодное, почти пустое пространство, из которого они появились.

То есть если вы продолжаете читать это, то не являетесь больцмановским мозгом. Значит, в наших предположениях о будущем Вселенной что-то в корне ошибочно. Есть ещё урок, который нам надо выучить. (Мы займёмся этим в разделе, посвящённом «проблеме меры».)

Аргумент Судного дня

Та идея, что вы должны быть типичным наблюдателем, весьма глубокая и имеет неожиданные следствия. Ещё одно много обсуждавшееся следствие — аргумент Судного дня, предложенный Брэндоном Картером в 1983 году.

Во время Второй мировой войны союзники по антигитлеровской коалиции успешно оценивали количество немецких танков по серийным номерам. Если первый захваченный танк имел № 50, это исключало гипотезу о том, что у противника имеется более тысячи танков, с вероятностью 95 %, поскольку вероятность захватить одну из первых 50 построенных машин составляет менее 5 %. Ключевое допущение состоит здесь в том, что первый захваченный танк можно считать случайным из референтного класса всех танков.

Картер подчёркивал, что если при рождении каждому человеку присваивался бы серийный номер, можно было бы применить этот же аргумент для оценки числа всех людей, которые когда-либо будут жить. При появлении на свет в 1967 году я оказался бы примерно 50-миллиардным родившимся на Земле человеком.[81] Если я случайный представитель всех людей, которые когда-либо жили, я могу исключить гипотезу о рождении в будущем более чем 1 трлн людей с надёжностью 95 %. Иными словами, крайне маловероятно, чтобы в будущем родилось более 1 трлн человек: в этом случае я оказался бы среди первых 5 % всех людей, — а это нельзя объяснить ничем, кроме маловероятного совпадения. И если мировое население стабилизируется на 10 млрд человек с ожидаемой продолжительностью жизни около 80 лет, человечество, каким мы его знаем, с вероятностью 95 % не дотянет до 10 000 года.

Если я верю, что Судный день будет вызван ядерным конфликтом (либо компьютерами, биотехнологией или любой другой технологией из появившихся после 1945 года), прогноз становится ещё более мрачным. Мой порядковый номер с того момента, когда возникли эти опасности, составляет 1,6 млрд, и я могу исключить с вероятностью 95 %, что после меня до 2100 года родится ещё 32 млрд человек. А ведь это предел с 95-процентной уверенностью: более вероятно, что конец человечества где-то неподалёку от нынешнего времени. Чтобы уйти от этого пессимистичного вывода, мне необходим некий априорный аргумент, объясняющий, почему я должен оказаться в числе первых 5 % людей, которым предстоит родиться под сенью этих технологий. (Мы вернёмся к экзистенциальной угрозе со стороны технологии в гл. 13.)

Некоторые люди очень серьёзно воспринимают аргумент Судного дня. Когда я встретил на конференции Брэндона Картера, он возбуждённо рассказал мне о последних данных, свидетельствующих о замедлении популяционного взрыва, и заявил, что он это предсказывал и что нам теперь следует ожидать, что человечество просуществует дольше. Другие с различных позиций критиковали этот аргумент. Например, всё становится гораздо интереснее, если существуют другие планеты с похожими на нас людьми. Рис. 11.10 иллюстрирует пример: общее число когда-либо родившихся сильно меняется от планеты к планете. Если вы знаете, что дела именно таковы, вы должны быть настроены оптимистичнее, чем предполагает стандартный аргумент Судного дня. В самом деле, если я верю в радикальную теорию, гласящую, что в пространстве-времени существуют лишь две населённые планеты, на которых от начала до конца истории живёт соответственно 10 млрд и 10 квадриллионов человек, то с вероятностью 50 % я нахожусь на планете, где появится квадриллион людей.

Рис. 11.10. Если вы знаете, что ваш порядковый номер при рождении — трехмиллиардный, то можете оценить, что лишь с 10-процентной вероятностью на вашей планете когда-либо родится более 30 млрд человек. Но, допустим, вам известно, что есть 6 планет, похожих на вашу, где общее число людей, родившихся за время существования цивилизации, составляет 1, 2, 4, 8, 16 и 32 млрд соответственно (каждый значок на рисунке соответствует 1 млрд человек). В этом случае вероятность того, что более 30 млрд человек будет когда-либо жить на вашей планете, составляет 25 %; есть четыре человека, имеющих ваш порядковый номер, и вы с равной вероятностью можете оказаться любым из них; 25 % живёт на очень удачливой планете внизу рисунка.

К сожалению, этот контраргумент вселяет ложную надежду. У меня нет такой информации, однако есть очень серьёзные основания считать, что теория о двух планетах ложна. Наблюдение, что мой порядковый номер при рождении составляет около 50 млрд, исключает данную теорию с надёжностью более 99,999 999 %: вероятность для случайного человека оказаться среди первых 50 млрд рождённых составляет лишь 0,0 000 005 %.

Почему Земля такая старая?

В марте 2005 года я имел удовольствие встретиться с Ником Бострёмом на конференции в Калифорнии, и мы вскоре открыли, что нас связывают не только проведённое в Швеции детство, но и восхищение большими вопросами. Под хорошее вино наша беседа повернула к сценарию Судного дня. Может ли Большой адронный коллайдер породить миниатюрную чёрную дыру, которая в итоге поглотит Землю? Можно ли создать страпельку,[82] которая катализирует превращение Земли в странную кварковую материю? Мои коллеги из МТИ, расчётам которых я доверяю, выяснили, что риск этого ничтожен. Но вдруг они упустили что-нибудь? Обычно меня успокаивает тот факт, что природа куда суровее машин. Частицы космических лучей, порождённые вблизи гигантских чёрных дыр, постоянно врезаются в Землю с энергией в миллионы раз более высокой, чем достижимая на наших ускорителях, и всё же Земля живёт и здравствует уже 4,5 млрд лет. Так что наша планета явно очень устойчива, и беспокоиться мне не стоит. По той же причине нет нужды тревожиться о других космических сценариях Судного дня, вроде космического «замерзания» с переходом пространства в другую, низкоэнергетическую фазу. В гл. 5 речь шла о смертельном космическом пузыре, расширяющемся со скоростью света и уничтожающем всех людей в то же мгновение, когда они его видят. Если мы всё ещё есть, значит, таких событий происходить не должно или они очень редки.

И тут у меня возникла жуткая мысль: успокаивающий меня аргумент содержит ошибку! Допустим, каждая планета каждый день имеет 50-процентную вероятность быть уничтоженной. Тогда подавляющее большинство их исчезнет за несколько недель, но в бесконечном пространстве с бесконечным числом планет их всегда бесконечное число, а их обитатели будут пребывать в блаженном неведении касательно своей судьбы. И если я случайный наблюдатель в пространстве-времени, мне следует ожидать, что я окажусь одним из множества наивных людей, которые не осознают, что они подобны овцам на скотобойне. Иными словами, тот факт, что моя область пространства ещё не уничтожена, ни о чём не говорит, поскольку все живые наблюдатели находятся в областях пространства, которые ещё не были уничтожены. Я по-настоящему занервничал. Я почувствовал себя так, как если бы оказался в зоопарке наедине с компанией голодных львов и обнаружил, что решётка, которая, как я думал, защищает меня, на самом деле оптическая иллюзия и львы её не видят.

Мы с Ником бились над этой проблемой, пока не нашли другое, не содержащее ошибок возражение на аргумент Судного дня. Земля образовалась примерно через 9 млрд лет после нашего Большого взрыва, и теперь совершенно ясно, что наша Галактика (и ей подобные) содержит множество подобных Земле планет, которые образовались на несколько миллиардов лет раньше. Когда мы считаем во всём пространстве-времени подобных нам наблюдателей, получается, что значительная их доля существовала задолго до нас. Теперь в сценарии, где планеты спонтанно уничтожаются с коротким периодом полураспада (скажем за день, за год или тысячелетие), почти все наблюдательные мгновения будут относиться к раннему периоду, и для нас крайне мала вероятность обнаружить себя ближе к концу игры на планете, развивающейся в таком ленивом темпе. Мы решили написать об этом статью и до глубокой ночи работали в вестибюле гостиницы. Я отправился спать, будучи на 99,9 % уверенным, что ни смертельные пузыри, ни чёрные дыры, ни страпельки в ближайший миллиард лет нам не грозят. Если, конечно, мы не сделаем какую-нибудь глупость из тех, что природа ещё не пыталась совершить…

Почему вы не моложе?

Если физика предусматривает некую ужасную уязвимость, делающую большинство планет короткоживущими, то следует считать, что мы живём на одной из первых образовавшихся обитаемых планет. Так что эта депрессивная теория исключается. К несчастью для инфляции, Алан Гут понял, что при некоторых вполне разумных условиях она предсказывает именно такой результат. Беспокоясь за своё детище, предсказывающее гораздо более молодую Землю, он назвал это парадоксом молодости. Примерно в 2004 году, когда я стал его коллегой в МТИ, я потратил много времени на размышления о том, как делать предсказания в мультиверсе. Я написал на эту тему статью, которая объёмом далеко превзошла все мои рекорды, и был удивлён, обнаружив, что парадокс молодости оказался ещё более жёстким, чем я думал.

Обычно инфляция длится вечно (гл. 5), удваивая объём пространства примерно каждые 10^–38 секунды и порождая беспорядочное пространство-время с бесчисленными Большими взрывами, происходящими в разные моменты времени, и бессчётным числом образующихся в разное время планет. Мы видели, что наблюдатель на любой планете будет рассматривать свой Большой взрыв в качестве момента окончания инфляции в своей части космоса. Лично для меня задержка между Большим взрывом и текущим наблюдательным мгновением составляет около 14 млрд лет. Теперь рассмотрим все одновременные наблюдательные мгновения: для некоторых время, прошедшее с момента их Большого взрыва, составляет 13 млрд лет, для других — 15 млрд, и т. д. Из-за безумного удвоения объёмов спустя секунду число Больших взрывов возрастёт в 2¹⁰³⁸ раз, поскольку объём за это время увеличится в 10³⁸ раз. По той же причине в галактиках рождается в 2¹⁰³⁸ раз больше наблюдателей. Это означает, что если я — случайный наблюдатель среди всех существующих в данный момент, то мой шанс оказаться во Вселенной на секунду моложе, в которой Большой взрыв произошёл секундой позднее, в 2¹⁰³⁸ раз выше! Это единица со ста триллионами триллионов триллионов нулей. Моя планета должна быть моложе, моё тело должно быть моложе, и всё вокруг должно казаться образовавшимся в страшной спешке.

Часть пространства, испытавшая свой Большой взрыв в более близкое время, будет горячее, поскольку у неё было меньше времени. Обнаружить себя в относительно холодной Вселенной крайне маловероятно, и возникает проблема холодности. Когда я рассчитал вероятность того, что измеренная температура космического микроволнового фона окажется ниже 3° над абсолютным нулём, у меня получилось 10^–1056, так что результат измерения этой температуры спутником COBE, составляющий 2,725 кельвина, исключает нашу основанную на теории инфляции историю с надёжностью 99,999…999 %, где после десятичной запятой следует сто миллионов триллионов триллионов триллионов триллионов девяток. Это нехорошо. В зале позора, где выставлены расхождения между теорией и экспериментом, этот результат побивает даже проблему устойчивости атома водорода из гл. 7 (28 девяток) и проблему тёмной энергии из гл. 4 (123 девятки). Итак, встречайте проблему меры!

Проблема меры: кризис в физике

Что-то пошло не так. Но что именно? Действительно ли вечная инфляция исключена? Посмотрим. Мы задали резонный вопрос о том, каких результатов измерений должен ожидать типичный наблюдатель. В качестве примера мы взяли температуру космического микроволнового фона. Поскольку мы рассматриваем вечную инфляцию, мы проанализировали пространство-время, содержащее множество наблюдательных мгновений, в которые измерено много разных температур. Так что мы не можем предсказать один-единственный ответ, а можем лишь указать вероятность для определённого диапазона температур. Само по себе это не конец света: в гл. 7 мы видели, что квантовая механика не даёт определённых ответов, а предсказывает лишь вероятности — и при этом является проверяемой и успешной научной теорией. И всё же проблема в том, что вычисленные нами вероятности указывают на то, что результаты наших наблюдений совершенно неправдоподобны, и это заставляет отбросить теорию, на которой мы основываемся.

Может ли дело быть в ошибке в вычислениях вероятности? Математика здесь, в принципе, очень простая: вероятности — это доли от числа всех наблюдательных мгновений в референтном классе, в которые измерена температура. Если существует только пять таких наблюдательных мгновений, в которые зарегистрированы значения 1, 2, 5, 10 и 12° над абсолютным нулём, то доля измерений менее 3° составит два из пяти, 2/5 = 40 % — тривиально! Но что если, как предсказывает вечная инфляция, существует бесконечно много таких наблюдательных мгновений, и доля измерений с результатом менее 3° — это бесконечность, разделённая на бесконечность? Как придать этому смысл?

Математики разработали элегантную схему, называемую предельным переходом, которая во многих случаях позволяет придать смысл выражению ?/?. Например, какую долю всех натуральных чисел 1, 2, 3, … составляют чётные? Существует бесконечное количество чисел, и среди них бесконечно много чётных, так что их доля составляет ?/?. Но если мы сосчитаем только первые n чисел, то получим разумный ответ, слегка зависящий от числа n, на котором мы остановились в подсчётах. Если увеличивать n, мы обнаружим, что с ростом n доля чётных чисел всё меньше варьирует. Если теперь взять предел, в котором n стремится к бесконечности, мы получим корректно определённый ответ, который вообще не зависит от n: ровно половина всех чисел — чётные.

Это кажется разумным, однако бесконечность коварна, и доля чётных чисел зависит от порядка, в котором мы их считаем. Если мы упорядочим числа так: 1, 2, 4, 3, 6, 8, 5, 10, 12, 7, 14, 16 и т. д., согласно той же схеме с пределом получится, что 2/3 чисел являются чётными. Дело в том, что, двигаясь по этому списку чисел, мы встречаем два чётных числа на каждое нечётное. Мы не жульничали, поскольку все чётные и нечётные числа рано или поздно появятся в списке; мы просто их переупорядочили. Соответствующим образом переупорядочивая числа, я могу доказать, что доля чётных чисел равна единице, делённой на номер вашего телефона.

Аналогично доля наблюдателей (из бесконечного их множества в пространстве-времени), получающих конкретный результат измерения, зависит от порядка, в котором вы их считаете. Космологи пользуются термином мера для обозначения схемы упорядочивания наблюдательных мгновений или, в более общем случае, для метода подсчёта вероятностей, связанных с этими досадными бесконечностями. Те безумные вероятности, которые я насчитал для проблемы холодности, соответствуют конкретной мере, и большинство моих коллег догадывается, что проблема не в инфляции, а именно в мере: оказывается, неверно говорить о референтном классе всех наблюдательных мгновений в фиксированное время.

В последние несколько лет появилась целая лавина интересных статей, предлагающих альтернативные меры. Доказано, что на удивление трудно найти такую меру, которая работала бы с вечной инфляцией: одни меры не справляются с проблемой холодности; другие терпят неудачу, предсказывая, что вы являетесь больцмановским мозгом; третьи говорят, что вид нашего неба должен быть искажён гигантскими чёрными дырами. Александр Виленкин недавно сказал мне, что находится в глубоком унынии: несколько лет назад он надеялся, что одна-единственная мера позволит обойти все подводные камни и что её простота и элегантность покажутся всем убедительными. Однако сейчас мы имеем множество мер, которые, похоже, дают различные, но разумные предсказания, и нет очевидного способа выбрать между ними. Но если вероятности, которые мы предсказываем, зависят от предполагаемой нами меры и мы сами можем придумать меру, дающую почти любой желаемый ответ, то это значит, что предсказать мы ничего не можем.

Я разделяю беспокойство Александра. Я считаю проблему меры сильнейшим кризисом современной физики. На мой взгляд, инфляция оказалась логически саморазрушительной. О ней всерьёз заговорили потому, что она давала верные предсказания (гл. 5): она предсказала, что типичные наблюдатели должны обнаружить вокруг себя плоское, а не искривлённое пространство (проблема плоской геометрии); они должны обнаружить, что температура их космического микроволнового фона почти одинакова во всех направлениях (проблема горизонта), а спектр мощности микроволнового фона похож на тот, который измерил спутник WMAP, и т. д. Но затем она предсказала, что бесконечное множество наблюдателей измеряет различные вещи с вероятностями, зависящими от меры, которой мы не знаем. А это означает, что инфляция, строго говоря, не даёт никаких предсказаний о том, что должны видеть типичные наблюдатели. Отзываются все предсказания, и в первую очередь заставившие нас принять инфляцию всерьёз. Полное саморазрушение. Новорождённая инфляционная Вселенная выросла в непредсказуемого подростка.

Буду объективным по отношению к инфляции: я не знаю лучшей конкурирующей космологической теории, и поэтому я не рассматриваю всё перечисленное в качестве аргумента против инфляции как таковой. Я просто понимаю, что нам нужно решить проблему меры, и догадываюсь, что когда мы её решим, некая форма инфляции сохранится. Более того, проблема меры не ограничивается инфляцией, а возникает в любой теории с бесконечным числом наблюдателей. В качестве примера вернёмся к квантовой механике без коллапса волновой функции. Рассуждения о квантовом бессмертии из гл. 8 критически зависят от существования бесконечного числа наблюдателей, чтобы некоторые из них выжили, а значит, мы не можем доверять никаким выводам, пока не решена проблема меры.

На рис. 11.11 показано, что субъективное бессмертие не требует квантовой механики. Для него достаточно параллельных вселенных — неважно, находятся ли два самолёта, изображённые на рисунке, в различных частях нашего трёхмерного пространства (мультиверсе I уровня) или нашего гильбертова пространства (мультиверс III уровня). Так что в самом общем виде рассмотрим произвольный мультиверсный сценарий, в котором некий механизм ежесекундно убивает половину всех ваших копий. Через 20 секунд в живых останется лишь один из миллиона (1 из 2²⁰) ваших первоначальных двойников. До этого момента наберётся 2²⁰ + 2¹⁹ + … + 4 + 2 + 1 ? 2²¹ наблюдательных мгновений секундной продолжительности, так что лишь в одном из 2 млн наблюдательных мгновений будет иметься воспоминание о выживании в течение 20 секунд. Как отметил Пол Олмонд, это означает, что выжившие столь долго должны исключать саму постановку вопроса, что они участвуют в эксперименте по изучению бессмертия, с вероятностью 99,99 995 %. Странная ситуация: начав с верной теории происходящего, вы сделали предсказание о том, что произойдёт (вы выживете); ваши наблюдения подтвердили правильность этого предсказания, а вы тем не менее меняете свои взгляды и утверждаете, что данная теория исключена! Более того, чем дольше вы ждёте, тем более странным кажется то, что вы остаётесь в живых (гл. 8). Спасение за счёт отключения электричества, падения астероида и т. д. заставило бы большинство людей поставить под вопрос свои представления о реальности.

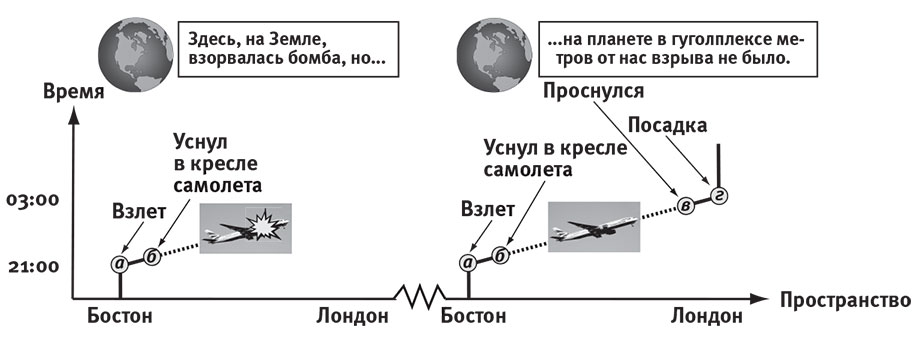
Рис. 11.11. На рис. 11.5 мы видели, что наблюдательное мгновение (в) воспринимается как продолжение наблюдательного мгновения (б), поскольку имеет с ним общие воспоминания. Однако (в) также воспринимается как продолжение (б), наблюдательного мгновения, принадлежащего двойнику, чей полёт идентичен — с тем исключением, что бомба террориста убивает всех пассажиров, прежде чем те проснутся. Если нет других двойников, то верное предсказание для (б) и для (б) состоит в том, что следующим будет восприниматься (в).

Бесконечные проблемы

О чём свидетельствует проблема меры? Вот моё мнение: в самом основании современной физики лежит ошибочное допущение. Провалы классической механики потребовали перехода к квантовой механике, и, я думаю, лучшие современные теории также нуждаются во встряске. Никто не знает достоверно, где корень проблемы. У меня есть подозрения на этот счёт. И вот мой главный подозреваемый: ?.

Собственно, у меня два подозреваемых: бесконечно большое и бесконечно малое. Под первым я подразумеваю ту идею, что пространство может иметь бесконечный объём, время может тянуться вечно, а физических объектов бесконечно много. Под вторым я подразумеваю континуум — ту идею, что литр пространства содержит бесконечное число точек, что пространство можно бесконечно растягивать без каких-либо нежелательных последствий и что в природе существуют величины, которые могут непрерывно изменяться. Два моих подозреваемых тесно связаны: в гл. 5 мы видели, что инфляция породила бесконечный объём путём неограниченного растягивания непрерывного пространства.

У нас нет прямых наблюдательных подтверждений существования чего-либо бесконечно большого или бесконечно малого. Мы говорим о бесконечных объёмах с бесконечным числом планет, но наблюдаемая Вселенная содержит лишь около 10⁸⁹ объектов (в основном фотонов). Если пространство и вправду есть континуум, то для описания даже чего-то столь простого, как расстояние между двумя точками, потребовалось бы бесконечное количество информации, задаваемой числом с бесконечным количеством десятичных знаков. На практике физики никогда не измеряли что-либо точнее, чем до 16 знаков.

Я помню, что не доверял бесконечности ещё будучи подростком, и чем больше я узнавал, тем подозрительнее становился. Без бесконечности не должно возникать проблемы меры — в результате вычислений мы всегда получим одну и ту же долю, независимо от порядка подсчёта. Без бесконечности не будет и квантового бессмертия.

Среди физиков мой скептицизм в отношении бесконечности оставил меня в меньшинстве. Математики обычно смотрят на бесконечность и континуум с подозрением. Карл Фридрих Гаусс, которого иногда называют величайшим математиком со времён античности, в 1831 году писал: «Я возражаю против употребления „актуально“ бесконечной величины как чего-либо завершённого, что никогда не позволительно в математике. Бесконечность — это скорее фигура речи, и её истинный смысл состоит в отсутствии предела, к которому некоторые отношения неограниченно приближаются, тогда как другим позволено возрастать без ограничений». Критикуя континуум и связанные с ним идеи, молодой коллега Гаусса Леопольд Кронекер заметил: «Целые числа сотворил Господь Бог, всё остальное — дело рук человеческих».[83] В XX веке, однако, идея бесконечности стала достоянием математического мейнстрима, и лишь немногие её критиковали вслух. Так, канадско-австралийский математик Норман Уилдбергер доказывал, что «вещественные числа — это шутка».

Почему современные физики и математики столь влюблены в бесконечность, что почти никогда не ставят её под вопрос? Главным образом потому, что бесконечность — это чрезвычайно удобное приближение, и пока мы не нашли подходящей альтернативы. Рассмотрим, например, воздух. Отслеживание положений и скоростей октиллионов атомов было бы безнадёжным усложнением дела. Но если игнорировать тот факт, что воздух состоит из атомов, и вместо этого использовать в качестве приближения континуум — непрерывную среду, которая обладает плотностью, давлением и скоростью в каждой точке, то окажется, что идеализированный воздух подчиняется простому, красивому уравнению. Оно описывает почти всё, что нас может интересовать — от характера распространения в воздухе звуковых волн до того, как возникает ветер. И всё же, несмотря на удобство, воздух не является непрерывным. Не может ли то же самое относиться и к пространству, времени и прочим «строительным материалам» нашего физического мира?