Уравнения Максвелла

В «Динамической теории электродинамического поля» Максвелл начинает все заново. Работа «О физических силовых линиях» напоминала огромный Вопрос, касающийся выводов из одной спекулятивной Гипотезы, нуждающейся в поддержке от Природы. «Динамическая теория» следовала традиции «Начал», переходя от наблюдаемых фактов к системе основных уравнений.

В то время как Ньютон опирался на законы планетарного движения Кеплера, Максвелл в качестве основы взял четыре закона, открытые несколькими учеными ранее: два закона Гаусса, закон Ампера и закон индукции Фарадея. (Они описываются ниже, а также в разделе «Термины».) Максвелл выразил эти законы на языке электрического и магнитного флюидов Фарадея, который он сделал точным и математическим в своих более ранних работах.

Также Максвелл добавил свой собственный закон, дуальный закону Фарадея. Это дополнение не было основано на экспериментах[42]. Как мы уже говорили, Максвелл первоначально пришел к постулированию этого закона, работая со следствиями из своей абсурдной модели. В новой трактовке он показал, что новый закон необходим, чтобы сделать старые законы согласованными!

На цветной вклейке N воспроизведены уравнения Максвелла. То, что они могут быть представлены в рисунках, является важным аспектом их красоты! Эта система из четырех уравнений, объединяющих четыре уже известных закона с новым дополнением, сейчас всем известна как уравнения Максвелла. (В четырех уравнениях скрыто пять законов, поскольку одно из уравнений суммирует два физических явления.) Вплоть до настоящего времени они остаются лучшим фундаментальным описанием электромагнетизма и света.

Здесь я не могу устоять от того, чтобы воспроизвести действительное содержание уравнений Максвелла. После того как я их так разрекламировал, вам, возможно, будет любопытно в точности узнать, из-за чего весь этот шум!

Я пытался сделать это способом, который достаточно краток, точен и понятен. Но существует некоторое противоречие между этими целями, и в результате этот отрывок может показаться вам сложным. Я советую вам подходить к нему так, как вы, может быть, подходите к незнакомому произведению искусства – как к возможности, а не как к бремени. Вы можете вначале прочитать его бегло и рассмотреть картинки, чтобы получить общее представление. Затем вы сможете решить, хочется ли вам читать его более внимательно. И я надеюсь, что вы это сделаете, – в конце концов, уравнения Максвелла являются великим произведением искусства. Вы можете сделать это на досуге, поскольку в нашей дальнейшей медитации не будет отсылок к этим деталям. Также вы можете справиться в «Терминах», где то же самое рассматривается с немного иных точек зрения. В комментариях я также указал несколько великолепных бесплатных веб-сайтов, где вы можете интерактивно изучать уравнения Максвелла.

Вначале я приведу неформальную версию, затем – более точную, в описаниях и рисунках для каждого из пяти физических законов, приводящих к четырем уравнениям Максвелла. Чтобы следовать за ходом мысли, обратитесь к цветной вклейке N, поскольку мы прочтем ее всю, строчка за строчкой.

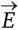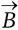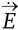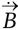Вначале разрешите дать пояснения к обозначениям на рисунках:  обозначает электрическое поле,  – магнитное поле, и  – скорости изменения этих величин во времени, Q – это электрический заряд, а  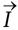– электрический ток. (Маленькие стрелки напоминают о том, что все эти величины векторные – они имеют направление, так же как и величину.)

Теперь перейдем к законам:

• Электрический закон Гаусса выражает равенство между потоком электрического поля, уходящим из некоторого объема, и электрическим зарядом внутри этого объема. Он говорит о том, что электрические заряды – это точки зарождения электрических силовых линий (или точки их завершения). Они находятся там, где электрические силовые линии могут начаться или закончиться.

Определение потока проще всего понять по ассоциации с течением жидкости. Электрическое поле, как мы уже обсудили, это величина, которая в каждой точке имеет численное значение и направление. Поле скоростей в текущей жидкости имеет такой же характер. Если у нас есть некий объем и поле скоростей, мы можем рассчитать, насколько быстро жидкость покидает этот объем. Это, по определению, и есть поток жидкости, покидающей данный объем. Если мы произведем над электрическим полем те же самые математические операции, которые мы только что провели над полем скорости жидкости, чтобы высчитать его поток, мы получим (по определению) поток электрического поля.

• Магнитный закон Гаусса гласит, что поток магнитного поля, исходящего из любого объема, равен нулю. Магнитный закон Гаусса, конечно, очень похож на электрический закон Гаусса, но с дополнительным упрощением – ведь магнитного заряда не может быть! Он говорит, что у магнитных полей нет источников – магнитные силовые линии никогда не могут завершиться, но должны вместо этого продолжаться вечно или замыкаться сами на себя.

• Закон Фарадея особенно интересен, потому что он включает время. Закон устанавливает соотношение между электрическими полями и темпом изменения магнитных полей. Закон гласит, что, когда магнитные поля изменяются во времени, они порождают электрические поля, закручивающиеся вокруг магнитных.

Чтобы точно сформулировать закон Фарадея, рассмотрим кривую, которая образует границу поверхности. Закон Фарадея утверждает равенство циркуляции электрического поля по этому контуру (с отрицательным знаком) скорости изменения магнитного потока через поверхность. Циркуляцию, как и поток, проще всего понять через ассоциацию с полем скоростей в течении жидкости. Мысленно расширим нашу кривую, превратив ее в узкую трубку, и рассчитаем количество жидкости, проходящей по этой трубке в единицу времени. Это и будет циркуляция потока жидкости. Если мы проведем над электрическим полем те же математические операции, которые мы провели над полем скоростей жидкости, то получим (по определению) циркуляцию электрического поля.

Наконец, чтобы быть совершенно точными, мы должны разрешить неоднозначность с направлением: определяя циркуляцию, в каком направлении мы должны двигаться вокруг кривой? Определяя поток, в каком направлении мы должны двигаться сквозь поверхность? Чтобы получить определенное соотношение, мы должны установить соответствие между существующими вариантами выбора. Стандартным способом является так называемое правило правой руки: если мы двигаемся по кривой в направлении, указанном четырьмя пальцами правой руки, тогда мы должны считать поток направленным в сторону большого пальца.

• Закон Ампера устанавливает соотношение между магнитными полями и электрическими токами. Он гласит, что электрические токи порождают магнитные поля, закручивающиеся вокруг них.

Чтобы точно сформулировать закон Ампера, рассмотрим кривую, образующую границу поверхности. Закон Ампера утверждает равенство между циркуляцией магнитного поля вдоль кривой и потоком электрического тока сквозь поверхность.

Стоит отметить, что одни и те же понятия потока и циркуляции повторяются в этих законах несколько раз. Поток и циркуляция – это самые основные способы для мысленного восприятия полей. Они заключают в себе соответственно силовые линии, устремляющиеся прочь по прямой и завивающиеся в петли. Их выдающееся положение в физических законах – это дар Материи Уму.

Но когда Максвелл собрал все эти четыре закона вместе, он нашел… противоречие! (Но пятый закон Максвелла исправляет его.) Чтобы увидеть это, обратимся к цветной вклейке О.

Проблема возникает в том случае, если вы пытаетесь применить закон Ампера в ситуации, когда электрический ток прерывается. На иллюстрации на вклейке О показан электрический ток, втекающий в и вытекающий из пары пластин, разделенных промежутком. (Специалисты могут узнать модель конденсатора.) Согласно Амперу, магнитная циркуляция вдоль контура равна потоку тока, проходящему сквозь любую поверхность, которую он ограничивает. Но здесь мы получим различные значения для потока в зависимости от того, какую поверхность возьмем! Если мы берем диск внутри промежутка между пластинами (на иллюстрации он обозначен синим), мы получаем нуль. Если мы возьмем полусферу, которая пересекает провод (на иллюстрации показана желтым), мы получим полный поток.

Ой-й!

Чтобы справиться с этим противоречием, нам нужно что-то новое. Благодаря более ранней работе со своей моделью у Максвелла был готов

• Закон Максвелла, нечто вроде обратного утверждения к закону Фарадея с заменой ролей электрического и магнитного полей. Он гласит, что, когда электрические поля меняются со временем, они порождают магнитные поля, закручивающиеся вокруг них.

Диск, поставленный в промежуток между пластинами, не перехватывает поток тока, но он перекрывает изменяющееся электрическое поле. Желтая полусфера дает магнитную циркуляцию в соответствии с законом Ампера, тогда как голубой диск дает магнитную циркуляцию в соответствии с законом Максвелла, но оба они приводят к одному и тому же результату! Тем самым противоречие уходит. После добавления закона Максвелла полная система уравнений Максвелла становится согласованной.

В этом качестве – как приводящий в порядок версию «Динамической теории электродинамического поля» – закон Максвелла приобрел новый статус. Он потерял свои связи с механическими моделями, вихревыми атомами и смазкой из перекатывающихся сфер. Теперь мы видим, что он был логически необходим для согласования всех остальных законов, которые были выведены из экспериментов.