Почти попали

Вот что происходит, если выполнить эту программу (илл. 40). Как вы можете видеть, она почти работает – три линии, представляющие интенсивности различных взаимодействий, почти сходятся в одной точке. Но не совсем.

Я хочу дать некоторую дополнительную информацию об илл. 40 на случай, если вам захочется понять ее во всех деталях. Чтобы представить результат в настолько простом виде, насколько это возможно, – три прямых линии! – мне пришлось сделать два не самых обычных шага, которые обозначены в подписях к осям. Я сделал так, что по вертикали отложены обратные интенсивности, так что чем выше интенсивность взаимодействия, тем ниже точка на графике. (Этот, на первый взгляд, странный выбор имеет еще одно важное преимущество, которое проявится на илл. 41.) На горизонтальной же оси я использовал логарифмическую шкалу. Таким образом, каждый шаг вправо уменьшает расстояние и увеличивает энергию, которая нам нужна, чтобы получить доступ к таким расстояниям, в 10 раз! Следовательно, наш расчет, несмотря на его скромный вид, возносит нас далеко вверх от энергий, которых в настоящий момент достигают ускорители. Толщина линий обозначает их экспериментальную и теоретическую неопределенности.

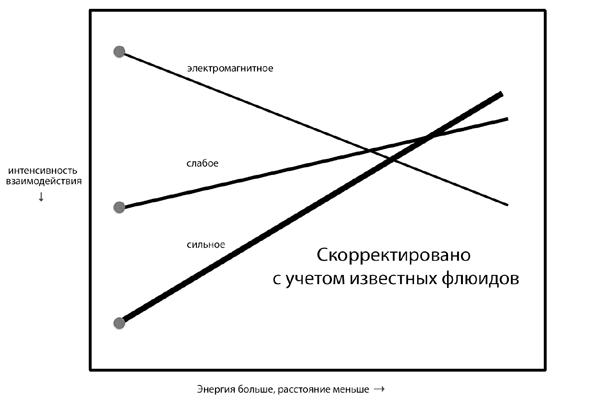
Илл. 40. Как только внесены поправки на влияние известных квантовых флюидов, мы находим, что объединение почти имеет место и остается лишь незначительное отклонение

Мы надеялись обнаружить, что интенсивности основных взаимодействий становятся равными, когда их измеряют на коротких расстояниях или исследуют на высоких энергиях. Мы берем значения, измеренные на расстояниях (или энергиях), которые нам предоставляют самые мощные из имеющихся ускорителей, а затем используем теорию и расчет, чтобы сделать оценку значений на еще более коротких расстояниях (или более высоких энергиях). На этой иллюстрации опорные точки, представляющие реальные измерения, видны слева, они выделены большими точками. Более короткие расстояния, «доступные» путем расчета, простираются направо. Вы видите, что модель почти работает – эти три линии почти сходятся в точку, – но не совсем.

В этот кризисный момент мы могли бы искать утешение в идеях известного философа Карла Поппера. Поппер учил, что цель науки состояла в том, чтобы порождать опровержимые (фальсифицируемые) теории. Мы создали теорию, которая является не просто опровержимой, а опровергнутой. Миссия выполнена!

Такое утешение звучит фальшиво. Мы разработали красивую идею, которая казалась многообещающей, и она почти сработала. Красота драгоценна. Мы не должны сдаваться слишком быстро.

А теперь я хотел бы рассказать вам историю о том, как вместе с несколькими друзьями мы обнаружили возможное решение. Но сначала я должен представить вам еще одного друга: SUSY.