Термины
[88]
Этот раздел содержит определения и короткие комментарии к научным понятиям, которые могут быть не знакомы широкому кругу читателей и использованы в этой книге. В некоторых случаях (например, «энергия» или «симметрия») они объясняют общеупотребительные слова, которые мы используем особым образом – обычно в более узком и специальном значении, чем в их повседневном применении. Я старался, насколько было возможно, сделать его органичной частью единого целого, используя в комментариях темы и примеры из основного текста. Здесь вы также найдете несколько идей, некоторые из которых красивы – их мне очень хотелось включить в текст, но не удалось сделать это, сохранив гладкость повествования. Во многих случаях мне пришлось пожертвовать точностью и математической строгостью ради краткости и доступности.
Замечание по оформлению текста: курсив используется для обозначения заглавного слова или словосочетания каждой статьи, чтобы отметить основные места, где оно встречается в статье, а иногда для постановки смыслового ударения. Жирный шрифт указывает на существенное использование терминов, про которые есть отдельные статьи.
Адрон
Hadron
Будучи подверженными сильному взаимодействию, кварки, антикварки и глюоны могут связываться и образовывать большое количество разнообразных небольших объектов. Адрон – это общий термин для объектов такого типа. Протоны и нейтроны являются примерами адронов, так же как и атомные ядра. Все остальные известные адроны крайне нестабильны, их время жизни варьируется от нескольких наносекунд (миллиардная доля секунды, или 10–9 секунд) до гораздо меньших времен.
Большую часть адронов можно полуколичественно понять в рамках кварковой модели. (См., если нужно, Качественный и количественный.) Согласно кварковой модели, адроны делятся на два обширных класса: барионы и мезоны. Барионы (класс, включающий протоны и нейтроны) – это связанные состояния, содержащие три кварка, в то время как мезоны – это связанные состояния, содержащие один кварк и один антикварк. (Также существуют антибарионы, состоящие из трех антикварков. См. Антивещество.) В более точном представлении, основанном на квантовой хромодинамике (КХД), эти две основные схемы должны считаться каркасом, который дополнен глюонами и дополнительными кварк-антикварковыми парами.
Широко распространено мнение о том, что существуют адроны, которые выходят за рамки обеих схем кварковой модели, такие как «глюболы»[89], где глюоны преобладают над кварками и антикварками. Эта идея является предметом исследований в настоящее время.
(См. также статью Квантовая хромодинамика (КХД) и подробное обсуждение в главе «Квантовая красота III», часть 2.)
Альфа-частица
Alpha particle
На начальном этапе экспериментального изучения радиоактивности Эрнест Резерфорд разделил излучаемый материал на альфа-, бета– и гамма-лучи. Они различались по способности проникать в вещество, по восприимчивости к отклонению магнитным полем и по другим свойствам. Дальнейшие исследования показали, что альфа-лучи состоят из ядер атома гелия-4, т. е. являются связанными комбинациями двух протонов и двух нейтронов. Мы называем эти ядра альфа-частицами.
Аксиальный вектор
Axial vector
См. Четность, где это понятие появляется в естественном для него контексте.
Аксиальный ток
Axial current
Аксиальные токи – специальный класс токов, которые не меняют знак при пространственной инверсии (преобразовании четности). Таким образом, аксиальные токи определяют поля аксиальных векторов. Я упомянул это довольно хитрое понятие, когда искал убедительный для редакторов журнала Physical Review Letters повод для введения термина «аксион».
Аксион
Axion
Аксион – это гипотетическая частица, чье существование сделало бы Главную теорию еще красивее. В настоящее время аксионы также являются превосходными кандидатами на космологическую темную материю.
Главная теория имеет множество достоинств, но также обладает некоторыми эстетическими недостатками. Среди последних есть следующий.
Мы экспериментально наблюдаем, что законы физики в очень хорошем приближении (но не полностью) инвариантны относительно изменения направления времени. Проще говоря, если взять видеозапись любого физического эксперимента и просмотреть ее задом наперед, то запись все равно будет показывать события, которые подчиняются фундаментальным законам физики. Конечно, если вы возьмете видеозапись из повседневной жизни и развернете ее задом наперед, то, что вы увидите, не будет похоже на повседневную жизнь. Но в субатомном мире, где самые фундаментальные законы действуют очевиднее всего, это различие пропадает. Поэтому мы говорим, что законы физики практически полностью инвариантны относительно обращения времени вспять или, по-другому, что они обладают симметрией относительно обращения времени (Т-симметрией).
Свойство законов обладать Т-симметрией согласуется с Главной теорией, но вообще-то последняя этого не требует. Существует такое взаимодействие между цветными глюонами, которое согласуется со всеми известными общими принципами, включая квантовую теорию, теорию относительности и локальную симметрию, а следовательно, согласно Главной теории, оно «возможно» – но его существование нарушало бы T-симметрию.
Просто заявить, что в действительности такого взаимодействия не происходит, было бы последовательно, но неубедительно. Более уместным представляется ответ, который впервые предложили Роберто Печчеи и Хелен Квинн – они объяснили это «совпадение», расширив Главную теорию таким образом, чтобы она включала дополнительную симметрию. Если сделать это подходящим образом, то можно объяснить малость нарушения Т-четности. (Выдвигались и другие возможные объяснения, но ни одно из них не прошло испытание временем.) Это расширение Главной теории не остается без последствий: как заметили мы со Стивеном Вайнбергом, из него следует существование новой, очень легкой частицы с замечательными свойствами – аксиона.
Аксионы пока не открыты экспериментально, но то, что мы их не наблюдаем, ни о чем не говорит, так как теория предсказывает, что аксионы должны очень слабо взаимодействовать с обычным веществом, и на сегодняшний день ни один эксперимент не достиг нужной чувствительности. Во время написания этой книги несколько групп экспериментаторов по всему миру активно работали над тем, чтобы найти подтверждения существования аксионов или доказательно исключить их существование.
Можно подсчитать, сколько аксионов образовалось в момент Большого взрыва. Из этих вычислений следует, что Вселенная пронизана аксионным газом, из которого также может состоять космологическая темная материя.
Анализ
Analysis
В физике, химии и математике словом «анализ» обычно называют процесс изучения чего-либо путем исследования его частей. В этом значении «холистический (целостный) анализ» – это оксюморон, а психоанализ – что-то совсем другое.
Два интересных примера анализа – разделение света на спектральные цвета и анализ функций путем изучения их вариаций на небольших масштабах, как в (дифференциальном) исчислении.
Анализ и Синтез
Analysis and Synthesis
«Анализ и Синтез» – это фраза Ньютона, описывающая стратегию достижения полного и глубокого понимания некоторого класса объектов путем досконального изучения поведения его простейших составляющих (анализ) и затем построения целого из частей (синтез). Ньютон сам с большим успехом применил эту стратегию при изучения света, при изучении движения и при изучении математических функций.
Анализ и Синтез – это более изящный, уместный и исторически обоснованный способ выразить то, что часто называют редукционизмом, и который следует предпочесть вне спора.
Аналоговый
Analog
Если некая величина может изменяться гладко или, как часто говорят, непрерывно, мы говорим, что это аналоговая величина. Аналоговые величины противопоставляются цифровым, которые могут принимать только дискретный ряд значений, и таким образом могут изменяться только скачками. В современных основаниях физики длина и продолжительность времени – аналоговые величины.
Девиз Пифагора «Число есть сущность всех вещей» в пределе можно интерпретировать так, что все величины являются в своей основе цифровыми. Однако невозможность выразить одновременно сторону и диагональ квадрата как кратные одной и той же единицы, а также апории Зенона о движении стали первыми предупреждениями о том, что у такого взгляда есть трудности.
Цифровые величины обладают большими преимуществами для вычислений и передачи информации, так как позволяют исправлять небольшие ошибки. Так, например, если вы знаете, что правильный результат вычисления может быть только 1 или 2, а ваш приближенный расчет дает 1,0023, вы можете заключить, что правильный ответ 1, если только ваше приближение не очень плохое.
Если единица дискретности достаточно мала, цифровая величина может стать хорошим приближением для величины, которая на самом деле является аналоговой. Например, цифровая фотография может состоять из черных точек, которые расположены так близко, что для человеческого глаза, с его несовершенным разрешением, они будут казаться плавно меняющимися оттенками серого, которые зависят от плотности точек.
Математическое описание аналоговых величин обычно использует действительные числа, в то время как простейшие цифровые величины описываются натуральными числами.
Антивещество, античастицы
Antimatter/antiparticle
В 1928 г. Поль Дирак предложил новое уравнение, которое мы сегодня называем уравнением Дирака, для описания поведения электронов в квантовой механике. Из этой работы вытекало существенное предсказание: должна существовать античастица, позитрон, с такими же массой и спином, как и у электрона, но с противоположным зарядом. Этот позитрон, который также называют антиэлектроном, является античастицей электрона. Более поздние работы показали, что это явление – куда более общий результат квантовой механики и специальной теории относительности: для каждой частицы существует соответствующая ей античастица, которая имеет те же массу и спин, но противоположные значения электрического заряда, а также слабого заряда, цвета сильного взаимодействия и спиральности.
Антиэлектроны (позитроны) были открыты экспериментально в 1932 г. Антипротоны впервые наблюдались в 1955 г. Сейчас было бы крупным потрясением обнаружить частицу, у которой нет античастицы. Фотоны являются собственными античастицами. (Это возможно потому, что они являются электрически нейтральными и не несут никаких других зарядов.)
Когда частица встречается со своей античастицей, они могут аннигилировать в «чистую энергию» – что означает на практике любую из широкого разнообразия групп частиц и их античастиц. Например, любая частица и ее античастица могут аннигилировать в два фотона или в пару нейтрино-антинейтрино, хотя это обычно не самые вероятные исходы. Задачей Большого электрон-позитронного коллайдера LEP[90] в CERN, который был предшественником Большого адронного коллайдера LHC и занимал тот же самый огромный тоннель, было изучение аннигиляции электронов и позитронов, разогнанных до больших скоростей и движущихся в противоположных направлениях.
Хотя термин античастица имеет ясное и точное научное значение, термин антивещество, хотя и бывает полезен, немного более сомнительный, или лучше сказать немного наивный. Чтобы понять это словоупотребление, мы должны начать с (такого же сомнительного и наивного) определения «вещества», противоположностью которого оно является. В этом определении мы говорим, что некоторые частицы, из которых мы состоим и с которыми встречаемся в обычной жизни – т. е., u и d кварки и электроны, – это «вещество». В соответствии с этим определением мы включаем в понятие вещества их близких родственников – т. е. все виды кварков и все виды лептонов (кварки u, d, c, s, t, b; лептоны e, µ, ?, ?e, ?µ, ??), в то время как их античастицы мы называем антивеществом. Фотоны при таком делении не попадают по своей природе ни в одну из групп, так как они являются собственными античастицами. В указанном смысле единственное, что отличает «вещество» от «антивещества», это то, что первое более распространено, по крайней мере в нашей части Вселенной. Если бы мы вдруг заменили все частицы в мире их античастицами (и одновременно совершили бы преобразование четности, поменяв местами правое и левое), было бы очень сложно сказать, в чем разница!
Мне кажется, что термин «антивещество» скорее способен запутать, а не прояснить что-либо, и в этой книге я его избегал. Когда я говорю о «веществе», без пояснений, я имею в виду все формы вещества, включая (к примеру) антикварки, фотоны и глюоны.
Антисимметричный
Antisymmetric
Мы говорим, что некоторая величина симметрична относительно преобразования или что величина обладает симметрией, когда она не меняется при этом преобразовании. Мы говорим, что величина антисимметрична относительно преобразования, когда она меняет знак при этом преобразовании. Это применимо к численным величинам, а также к векторам и к функциям, потому что во всех этих случаях можно говорить об изменении знака.
Примеры: Координаты точек на прямой антисимметричны относительно поворота прямой на 180° относительно начала координат. Электрический заряд антисимметричен относительно преобразования, которое превращает частицы в их античастицы (см. Антивещество).
Фундаментальная характеристика фермионов состоит в том, что квантово-механическая волновая функция, описывающая систему идентичных фермионов, антисимметрична относительно преобразований, в которых любые два из них меняются местами.
Антропный аргумент, антропный принцип
Anthropic argument / anthropic principle
Антропный аргумент в первом приближении имеет следующую форму:
«Мир должен быть таким, какой он есть, чтобы я мог существовать».
Перед тем как обсуждать более сложные тонкости, давайте рассмотрим антропный принцип в этой самой простой форме.
Важно разделять два аспекта этого базового антропного аргумента: его истинность и его объяснительную силу. (См. связанное с этим обсуждение в статье Непротиворечивость и противоречие.) В зависимости от того, насколько узко определено понятие «Я», в антропном принципе может быть немалая доля тривиальной истины. Если «Я» подразумевает углеродную форму жизни с человеческой физиологией, которая жила подобно тому, как живу я (что, помимо прочего, включает чтение научных книг, в которых делаются сильные, конкретные утверждения об окружающем мире), тогда, пожалуй, конечно, законы физики, как мы их знаем, не говоря уже о многих других фактах о планете Земля, истории Европы, цвете глаз моих детей и т. д., не могут сильно отличаться от тех, что есть, так как эти отличия вскоре исключат мое существование. Так что базовый антропный аргумент, если воспринимать его буквально, верен. Но этот истинный аргумент имеет очень небольшую объяснительную силу, в основном потому, что существование «меня» – это такое всеобъемлющее предположение, включающее все, что я испытал или когда-либо испытаю, что оно не оставляет ничего, что нужно было бы еще объяснять!
Более сложные версии антропного аргумента должны основываться на менее жестких определениях «Я». Мы можем, например, потребовать, чтобы мир с его основными законами и историей давал возможность появления какому-то виду разумных или обладающих сознанием наблюдателей. Если бы это было не так, то его нельзя было бы наблюдать – да и черт бы с ним! Однако очень сложно определить, что имеется в виду под разумными наблюдателями, а также очень сложно понять, после того как вы определились с формулировкой, какого рода законы и история обуславливают появление разумных наблюдателей. Мне трудно представить, что такие размытые, скользкие идеи приведут нас к значительной объяснительной силе.
Примечательно, что самые глубокие достижения в понимании мира, такие как Главная теория, включают в себя такие концептуальные понятия, как относительность, локальная симметрия и основы квантовой теории, которые абстрактны по форме и универсальны по возможности применения. Эти принципы совсем не выглядят похожими на антропный принцип! Очевидно, что в мире происходят вещи, которые выходят за рамки его желания произвести «меня».
В целом антропные аргументы по своей природе смещают центр дискуссии от объяснения к допущению. Так как они компрометируют объяснительную силу, их в принципе следует избегать. Но в подходящих, очень специальных обстоятельствах аргументы в духе антропных могут быть одновременно правомерными и полезными[91]. Для ознакомления с примерами, которые могут оказаться интересными, см. Темная энергия, Темная материя.
Аромат
Flavor
Существует шесть различных видов, или ароматов, кварков. В порядке возрастания массы они обозначаются u (от английского up – верхний), d (down – нижний), s (strange – странный), c (charm – очарованный), b (bottom или beauty – прелестный), t (top – топ-кварк). Каждый из них «обитает» в трехмерном цветовом пространстве свойств, и (следовательно) все они ведут себя одинаково, если говорить о сильном взаимодействии. Кварки u, c и t имеют электрический заряд, равный 2/3 заряда протона, тогда как d, s и b имеют электрический заряд, равный –1/3 заряда протона. Они по-разному и немного сложно ведут себя относительно слабого взаимодействия – см. Семейство.
Глубокое значение этого избытка видов кварков если и существует, то на настоящий момент неясно. Из всех кварков только u и d играют большую роль в современном природном мире, поскольку обильно представлены в протонах и нейтронах.
Также есть аналогичный избыток лептонов; в этом случае говорят о различных ароматах лептонов.
Асимптотическая свобода
Asymptotic freedom
Сильное взаимодействие между двумя кварками изменяется под действием непрерывной спонтанной активности квантовых полей, которыми пронизано пространство. Сила взаимодействия ослабевает при сближении кварков и увеличивается при их удалении друг от друга. Это называется асимптотической свободой.
У асимптотической свободы есть множество следствий и применений, которые подробно изложены в тексте.
См. также Конфайнмент и Перенормировка (ренормализационная группа.)
Атомное число
Atomic number
Атомное число ядра – это число протонов, которое оно содержит. Атомное число ядра определяет его электрический заряд и, таким образом, его влияние на электроны, а следовательно, его роль в химии тех атомов и молекул, где оно фигурирует. Ядра, которые имеют одинаковые атомные числа, но разное число нейтронов, называются изотопами одного и того же химического элемента.
Пример: ядра углерода-12 (12C) содержат 6 протонов и 6 нейтронов, в то время как ядра углерода-14 (14C) содержат 6 протонов и 8 нейтронов. У этих ядер практически одинаковые химические свойства, поэтому и те и другие называются «углеродом», – но разная масса. Ядра углерода-14 нестабильны, и их распады можно использовать для датирования биологических образцов. (Когда организм умирает, он перестает получать извне новый углерод; следовательно, отношение количества углерода-14 к количеству углерода-12 в останках постепенно уменьшается. В атмосфере углерод-14 возобновляется благодаря столкновениям с космическими лучами.)
Барион
См. Адрон.
Бегущая волна
См. Стоячая волна и бегущая волна.
Бесконечно малые
Infinitesimal
В современной физике и математике мы определяем такие величины, как скорость и ускорение, с помощью операции взятия предела. Чтобы определить скорость частицы, мы рассматриваем перемещение за короткий промежуток времени, берем отношение и рассматриваем его предельное значение, беря все меньшие и меньшие интервалы. Это предельное значение по определению является скоростью.
В ранний период развития исчисления у его основоположников не было прочных оснований и четких определений. Они руководствовались интуицией и догадками. Лейбницу, в частности, очень нравилась идея о том, что вместо взятия предела можно рассматривать просто «бесконечно малое» приращение времени и соответствующее ему перемещение и брать отношение этих бесконечно малых. Однако ни Лейбниц, ни его последователи не сформулировали эту идею достаточно отчетливо. Она лежала без дела и была практически забыта многие десятилетия, пока математики XX в. не показали, что ее можно строго описать несколькими способами.
Идея о бесконечно малых похожа по духу – хотя и противоположна по направлению – на идею, приводящую нас к бесконечно удаленным точкам в проективной геометрии. В обоих случаях мы заменяем процедуру взятия предела конечными объектами.
Бесконечно малые предоставляют нам новый способ воплощения Идеального. Они пока еще не сыграли значительной роли в описании физического мира, но являются красивой идеей и поэтому заслуживают ее сыграть.
Бесконечно удаленная точка, точка схода
Point at infinity / vanishing point
Если мы встанем вертикально на плоской поверхности и посмотрим на две параллельные линии на этой плоскости, простирающиеся вдаль от нас, то увидим, что кажется, будто они сходятся, приближаясь к горизонту. Если мы мысленно нарисуем то, что видим, или если спроецируем геометрически эти линии на холст, естественно будет добавить как элемент изображения ограничивающую точку, где они действительно сходятся. Это будет бесконечно удаленная точка, или точка схода. Мы изображаем, углубляем и размышляем о приложениях этой конструкции в основном тексте.
Бозоны и фермионы
Boson/fermion
Элементарные частицы делятся на два обширных класса: бозоны и фермионы.
В Главной теории к бозонам относятся фотоны, виконы (бозоны слабого взаимодействия), цветные глюоны, гравитоны и бозоны Хиггса. В тексте я часто называю их частицами взаимодействия (силы). Бозоны могут быть созданы или уничтожены поодиночке.
Бозоны подчиняются принципу Бозе[92]. Грубо говоря, это значит, что два бозона одного вида особенно счастливы делать одно и то же. Фотоны являются бозонами, и именно принцип Бозе для фотонов делает возможным существование лазеров. Когда им дается такой шанс, вся совокупность фотонов пытается делать одно и то же, создавая узкий пучок спектрально чистого света.
В Главной теории кварки и лептоны являются фермионами. В тексте я часто называю их частицами материи.
Фермионы образуются и исчезают парами. В результате, если у вас есть один фермион, вы не можете просто так избавиться от него. Он может превратиться в другой вид фермиона, или в три, или в пять, а также в любое число не-фермионов (т. е. бозонов; см. выше) – но он не может раствориться, превратиться в ничто, не оставив следа.
Фермионы подчиняются принципу запрета Паули. Грубо говоря, это значит, что два фермиона одного вида не любят заниматься одним и тем же. Электроны являются фермионами, и принцип запрета Паули для электронов играет ключевую роль в структуре вещества. Он будет нашим проводником в главе «Квантовая красота II», в которой мы исследуем богатый мир углерода.
Большой адронный коллайдер
Large Hadron Collider
Большой адронный коллайдер, или БАК (LHC) – инструмент лаборатории CERN около Женевы. Главной целью проекта является исследование фундаментальных процессов при высоких энергиях, а следовательно, при меньших расстояниях и временах, чем это было когда-либо доступно ранее.
Это достигается следующим образом. Протоны ускоряют до очень высокой энергии движения и формируют из них два узких пучка. Пучки находятся внутри гигантского подземного кольца окружностью 27 км, где они циркулируют в противоположных направлениях, удерживаемые на траектории мощными магнитами. (Кольцо должно быть большим, а магниты мощными, потому что трудно отклонить такие высокоэнергетичные протоны от прямолинейного движения!) В нескольких точках наблюдения пучкам дают пересечься. Близкие прохождения высокоэнергетичных протонов, летящих в противоположных направлениях, приводят к «столкновениям», при которых огромное количество энергии концентрируется в очень небольшой области пространства, воссоздавая экстремальные условия, последний раз наблюдавшиеся во время самых ранних моментов Большого взрыва. Огромные, сложные «детекторы» – установки величиной десятки метров во всех трех измерениях, набитые ультрасовременной электронной техникой, – извлекают физическую информацию из последствий этих столкновений, которую затем анализируют большие команды высококвалифицированных ученых с помощью глобальной сети мощных компьютеров.
БАК – это более чем значимое дополнение нашей цивилизации к египетским пирамидам, римским акведукам, Великой Китайской стене и соборам Европы: все они являются потрясающими памятниками коллективным усилиям и технологическим достижениям людей.
В июле 2012 г. ученые, работающие на БАК, объявили об открытии бозона Хиггса. Чтобы узнать об этом больше, см. главу «Квантовая красота III», часть 3. В будущих экспериментах, при более высоких энергиях, будут проверены заманчивые идеи об объединении взаимодействий и о суперсимметрии, которые описаны в главе «Квантовая красота IV».
Буст
Boost
В научной литературе все чаще можно встретить термин «буст» по отношению к преобразованию, которое мы совершаем над системой, когда мысленно прибавляем некоторую постоянную скорость к движению всех частей системы или отнимаем ее. Этот термин, как мне кажется, произошел от первых ступеней[93] ракет-носителей, которые придают скорость полезному грузу. В книге я называю такие преобразования не бустом, а преобразованиями Галилея, в честь Галилео Галилея, который незабываемо подчеркнул их важность изящным мысленным экспериментом, в котором он приглашает нас на борт парусного судна в изолированную каюту (как описано в основном тексте). См. преобразования Галилея.
Вакуум, Пустота
Vacuum, Void
Под словом «вакуум» обычно понимают «пустое пространство, лишенное материи». Таким образом, говорят о «создании вакуума» путем выкачивания воздуха из сосуда, или о «вакуумных трубках» электронных ламп, или о «вакууме межзвездного пространства». Такое использование может стать неоднозначным по следующим причинам.
• То, что вы найдете, зависит от того, насколько вы готовы искать. «Вакуум» межзвездного пространства, например, пронизан микроволновым фоновым излучением; таким излучением, которое наши глаза ощутили бы как звездный свет; космическими лучами; потоками различных нейтрино; темной энергией и темной материей. На Земле инженеры вакуумной техники могут, приложив усилия, исключить первые две категории из некоторой области пространства и большую часть третьей, но никак не последние три. К счастью, причина того, что это настолько трудно, является также и причиной, почему это не имеет никакого значения для практических целей: потоки нейтрино, темная энергия, темная материя – и, возможно, нечто иное, о чем мы даже еще не знаем! – очень слабо взаимодействуют с обычным веществом.
• Что, как вам кажется, там есть, зависит от того, как упорно вы готовы думать. В нашей Главной теории даже идеально «пустое» пространство пронизывают множество квантовых флюидов: электромагнитный флюид, метрический флюид, электронный флюид, флюид Хиггса и т. д., а также метрическое поле и поле Хиггса.
Что именно имеют в виду люди, когда говорят «вакуум», обычно ясно из контекста, но в размышлении о фундаментальных принципах следует ясно осознавать, что слово «вакуум» не обозначает никакого четко определенного понятия. В частности, философское понятие Пустоты[94] – пространства, совершенно ничего не содержащего, – очень отличается от любого разумного понимания физического пространства где бы то ни было в современном физическом мире.
В современной физической космологии важно принять во внимание, что заполняющие пространство поля, такие как поле Хиггса:
• производят глубокие физические воздействия, как изменяя поведение материи, так и внося вклад в темную энергию;
• присутствуют в любом физически определенном вакууме (потому что они являются повсеместно распространенными и повсюду проникающими);
• могут – в экстремальных условиях – изменить свою интенсивность.
Комбинируя эти наблюдения, мы приходим к пониманию того, что могут существовать существенно отличающиеся реализации физического вакуума, где пронизывающие их поля отличаются по величине. Поведение материи в этих различных вакуумах может решительно отличаться, так же как и соответствующие плотности темной материи и темной энергии.
Будет интересно и изящно сказать, подытоживая эту ситуацию, что пространство само по себе – это материя такого рода, которая может существовать в различных фазах, так же как вода может существовать в виде жидкости, льда или пара. (См. Вселенная, видимая Вселенная и мультивселенная.)
Вектор, векторное поле
Vector/vector field
Векторы можно определить либо геометрически, либо алгебраически.
Геометрически вектор – математический объект, у которого есть одновременно величина и направление. Примеры:
• Если мы имеем две точки, скажем A и B, то прямолинейное перемещение, которое переводит A в B, является вектором. Его величина – это расстояние между A и B, а его направление – это направление от A к B.
• Скорость частицы является вектором.
• Электрическое поле в любой точке является вектором.
Алгебраически вектор – это просто последовательность чисел.
Эти два определения можно связать друг с другом, введя понятие координат. Векторы в примерах выше – это векторы в обычном трехмерном пространстве, которые соответствуют тройкам действительных чисел. Несколько интересных и важных вариаций на эту тему упомянуты в словарной статье о координатах.
Когда у нас имеется векторная величина, определенная в каждой точке пространства, мы говорим, что у нас есть векторное поле. Примеры:
• Если рассмотреть объем воды, ее различные части будут двигаться с разными скоростями. Эти скорости определяют векторное поле.
• Электрические и магнитные поля – это векторные поля.
• В каждой точке на экране компьютера интенсивности, с которыми светятся на экране красный, зеленый и синий цвета, являются последовательностью из трех чисел и, следовательно, определяют вектор. Таким образом, на экране вашего компьютера имеется векторное поле цветов.
Викон
Weakon[95]
Частично прелесть виконов состоит в том, что их можно определить несколькими дополнительными способами:
• Виконы – это W– и Z-частицы, которые наблюдаются в детекторах на ускорителях элементарных частиц.
• Виконы – это кванты флюида слабого взаимодействия, чья реакция на движение слабых зарядов вызывает слабое взаимодействие.
• Виконы – это воплощение особой локальной симметрии, симметрии вращения в пространстве свойств слабого заряда. Таково их наиболее красивое определение: оно показывает родство виконов с цветными глюонами, фотонами и гравитонами. Все они – воплощения локальной симметрии. Это напоминает нам о нашем Вопросе и ответе на него в Главной теории. Мы обнаруживаем связь «Реальное ? Идеальное» по мере того, как объекты и события реальности все более соответствуют понятиям, которые мы вводим, чтобы нарисовать анаморфную картину локальной симметрии.
Виртуальная частица
См. Квантовые флуктуации, виртуальная частица, поляризация вакуума и нулевые колебания.
Волновая функция
Wave function
В классической механике частицы в любой момент времени занимают некоторое определенное положение в пространстве. В квантовой механике описание частицы совершенно иное. Чтобы описать, скажем, электрон в квантовой теории, мы должны определить волновую функцию электрона. Волновая функция электрона задает его облако вероятности, плотность которого в некоторой области пространства обозначает относительную вероятность найти там этот электрон.
Здесь я набросаю более точное описание волновых функций электронов. Чтобы это описание не пропало для вас даром, вам понадобится по крайней мере мимолетное знакомство с комплексными числами и теорией вероятностей. Заключительная ремарка в этой словарной статье, обозначенная звездочкой (*), – это самая важная ее часть, с которой вам следует ознакомиться, даже если вы решили лишь бегло просмотреть или пропустить абзацы, ей предшествующие.
Волновая функция электрона – это поле комплексных чисел. Иначе говоря, каждой точке пространства в любой момент времени волновая функция приписывает комплексное число. Данное комплексное число называют величиной, или иногда амплитудой, волновой функции в данном месте и в данное время. Волновая функция подчиняется (относительно) простому уравнению, уравнению Шрёдингера, но сама по себе не имеет никакого очевидного физического смысла.
Что действительно имеет прямой физический смысл, так это поле положительных (или равных нулю) действительных чисел, которые мы получаем из волновой функции, возводя в квадрат модуль ее величины. Эта математическая операция позволяет нам перейти от волновой функции электрона к связанному с ним облаку вероятности. Вероятность обнаружения электрона в данной точке пространства и в данное время пропорциональна квадрату модуля величины волновой функции в этом месте и в это время.
Хотя он и описывается функцией, заполняющей пространство, не следует думать, что электрон – это протяженный объект. Когда мы наблюдаем электрон, он всегда наблюдается как цельный объект, со своей полной массой, электрическим зарядом и т. д. Волновая функция несет информацию о вероятности обнаружения целой частицы, не о распределении частей частицы.
Квантово-механическое описание двух или более частиц, как и следовало ожидать, также основано на волновых функциях. Оно вводит новое важное свойство: запутанность. Существенная новизна возникает уже для двух частиц, поэтому, чтобы изложить концепцию, насколько это возможно, конкретно и просто, я остановлюсь на этом случае.
Чтобы пояснить контекст, в котором возникает запутанность, позвольте мне начать с изложения предположительного описания двух частиц, которое могло бы показаться разумным, но на самом деле оказывается неправильным. Можно было бы предположить, что волновая функция для двух частиц имеет форму волновой функции одной частицы, умноженной на волновую функцию другой частицы. Отталкиваясь от такого предположения, если мы возьмем квадрат, чтобы получить облако вероятности, мы обнаружим, что совместная вероятность найти первую частицу в точке x, а также вторую частицу (скажем) в точке y, равна произведению вероятностей найти первую частицу в x и вторую в y. Другими словами, эти вероятности независимы. С физической точки зрения это неприемлемый результат, поскольку следует ожидать, что положение в пространстве первой частицы влияет на положение второй.
Правильное описание использует волновую функцию, являющуюся полем в шестимерном пространстве, координаты которого – это три координаты, описывающие положение первой частицы, и три координаты, описывающие положение второй частицы. Когда мы возводим этот объект в квадрат, чтобы получить совместную вероятность, мы обычно обнаруживаем, что две частицы больше не являются независимыми. Измерение положения одной из них влияет на вероятность того, где мы найдем другую. Поэтому мы говорим, что они запутаны.
Запутанность вовсе не является ни редким явлением в квантовой механике, ни непроверенным закоулком этой теории. Она возникает, например, когда мы вычисляем волновую функцию для двух электронов атома гелия. Спектр гелия был как измерен, так и рассчитан с большой точностью, и мы видим, что очень запутанные волновые функции квантовой механики дают результаты, которые соответствуют действительности.
* В контексте нашего Вопроса почти чудо – обнаружить, что шестимерное пространство, прекрасный плод творческого воображения, воплощено в чем-то столь определенном и конкретном, как атом гелия. Спектр этого атома, когда мы знаем, как его нужно читать, шлет нам открытки из шести измерений!*
Чтобы взглянуть на волновые функции еще с одного ракурса, см. в особенности обсуждение в статье о Квантовой теории.
(Заключительное замечание и предупреждение: термин «волновая функция» – это не самый лучший выбор для понятия, которое он обозначает. «Волна», вообще говоря, предполагает колебание, поэтому «волновая функция» предполагает функцию, которая колеблется, или функцию, которая описывает колебания в некоторой среде, но квантово-механические волновые функции не должны колебаться, и они не описывают колебания чего-то еще. Более подходящим названием могло бы быть «поле квадратного корня из вероятности электрона», но «волновая функция» слишком глубоко укоренилась в языке и литературе, чтобы всерьез рассматривать возможность изменения термина.)
Вселенная, видимая Вселенная и мультивселенная
Universe/visible Universe/multiverse
Современная физика открыла для космологии впечатляющие возможности, которые превосходят возможности обычного языка. Чтобы должным образом описать их, мы должны одновременно усовершенствовать и расширить повседневное употребление понятий. В частности, уже не годится расплывчатое использование слова «вселенная» в значении «все вокруг». Хотя даже научная литература еще не полностью последовательна в этих вопросах, я считаю, что было бы возможно и полезно различать три понятия, которые отражают наиболее современное научное употребление. Они, вероятно, дорастут до стандарта использования.
Видимая Вселенная состоит из всего, что доступно для наблюдения. Принципиальное ограничение возникает из-за конечной скорости света, которая (как мы полагаем) является предельной скоростью передачи информации, и из-за того, что прошло конечное время с момента Большого взрыва, который (как мы полагаем) является событием, раньше которого нельзя ничего увидеть. Ограниченные конечной скоростью и конечным временем, мы осознаем, что имеем доступ не дальше некоторого конечного расстояния, так называемого горизонта[96]. Надо отметить два момента:
• Горизонт растет по мере того, как время, прошедшее после Большого взрыва, становится больше. Таким образом, видимая Вселенная была меньше в прошлом, и мы можем ожидать, что она станет больше в будущем.
• Если мы обнаружим, что скорость света не является фундаментальным ограничением для передачи информации, или если мы научимся видеть то, что было до Большого взрыва, нам придется заново обдумать, что мы подразумеваем под видимой Вселенной.
Видимая Вселенная, которую мы видим сегодня, кажется примерно одинаковой повсюду. Астрономы находят звезды того же типа, организованные в виде примерно таких же типов галактик, повинующихся физическим законам такого же типа, как бы далеко и в каком бы направлении они ни смотрели[97]. Если мы предположим, что так и будет продолжаться дальше, по мере роста горизонта в будущем, мы придем к тому, что обычно называют Вселенной. Вселенная в этом смысле является консервативным логическим распространением нашего прошлого опыта наблюдения видимой Вселенной на неопределенное будущее.
Современная физика, однако, дала основания думать, что материальный мир может существовать в качественно различных формах, или фазах, примерно в таком же духе, как вода может существовать в виде льда, жидкости или пара. В этих отличающихся фазах пространство пронизано другими полями (или теми же самыми полями с другими интенсивностями). (См. Вакуум.) Поскольку эти поля в значительной степени определяют свойства материи, которая в них движется, эти различные фазы в сущности реализуют разные законы физики. Если такие отличающиеся области пространства существуют, то «Вселенная», как мы определили ее, – это не вся полнота действительности. Мы называем всю полноту действительности множественной Вселенной, или мультивселенной.
Идея о том, что существует мультивселенная, так что законы физики, которые мы наблюдаем, являются отчасти лишь особенностью того места, где нам случилось возникнуть, играет заметную роль в антропных аргументах.
Гармония
Harmony
Мы говорим, что музыкальные звуки находятся в гармонии или являются гармоничными, когда они хорошо звучат вместе. Происхождение этого психологического явления в физиологии в настоящее время остается неясным; в основном тексте схематично описана одна из возможных теорий. Музыкальное понятие о гармонии часто бывает расширено, по примеру Пифагора, до более общего понятия «о том, что хорошо сочетается».
Геодезическая линия
Geodesic
На искривленной поверхности может не быть никаких прямых линий, но геодезические линии являются для них самой близкой заменой. Геодезическая линия имеет свойство предоставлять кратчайший путь между любыми двумя ее соседними точками. Мы должны ограничиться «соседними» точками, поскольку после длительного «путешествия» геодезическая линия может вновь пройти рядом со своими более ранними частями, и тогда может существовать более короткий путь, идущий наперерез ее длинной траектории.
Пример: геодезические линии на сфере – это ее большие круги, получаемые сечением сферы плоскостью, проходящей через ее центр. Следовательно, экватор является большим кругом – и геодезической линией – на Земле, так же как и все меридианы. Трансполярные авиарейсы приблизительно следуют геодезическим линиям для экономии топлива.
Понятие геодезической линии, определенное таким образом, не ограничено поверхностями. Мы можем найти геодезические линии в искривленных пространствах с большим количеством измерений, а также – при соответствующем определении расстояния – в пространстве-времени.
Гиперзаряд
Hypercharge
Средний электрический заряд каждой сущности Главной теории называется гиперзарядом. (Эти сущности определяются в главе «Квантовая красота III», часть 4.)
Существует сложная связь между слабым взаимодействием, гиперзарядом и электромагнетизмом, которую я обошел вниманием в основном тексте. Потребовалось бы несколько страниц сухого текста, чтобы ее объяснить, и это объяснение пролило бы не слишком много света на наши основные вопросы. В примечаниях в конце книги я даю две ссылки, воспользовавшись которыми, вы сможете найти больше информации на эту тему.
Главная теория
Core theory
В этой книге Главной теорией называются господствующие теории сильного, слабого, электромагнитного и гравитационного взаимодействий, воплощающие принципы квантовой теории и локальной симметрии (включая общую теорию относительности – локальную версию галилеевой симметрии).
Главная теория, или часть ее, не включающая гравитацию, часто называется Стандартной моделью. По причинам, которые я объяснил в тексте книги, ей нужно лучшее название.
(Почему кому-то может прийти в голову исключать гравитацию при определении Главной теории? Часто говорят, что существует фундаментальный конфликт между квантовой механикой и общей теорией относительности, а иногда также заявляют, что этот конфликт влечет за собой парализующий физику кризис. Оба этих утверждения являются преувеличением, а второе явным образом вводит в заблуждение. Например, астрофизики регулярно сочетают общую теорию относительности и квантовую механику в своей работе, не встречая серьезных затруднений.
Общую теорию относительности можно ввести в уравнения Главной теории особым, искусственным способом, используя тот же самый глубокий принцип – локальную симметрию, – который мы привыкли использовать для остальных взаимодействий. Правила квантовой теории при этом продолжают действовать.
Определенная таким образом Главная теория не способна дать убедительные ответы на мысленные эксперименты касательно некоторых аспектов физики черных дыр, и ее уравнения становятся сингулярными и непригодными, когда мы осуществляем экстраполяцию к началу космологического Большого взрыва, а значит, это не есть Теория всего. Но мы и так это знаем благодаря проблемам семейств, темной энергии, темной материи и некоторым другим. Тем не менее это последовательная, фальсифицируемая, сильная и экономная теория. Вполне возможно и разумно включить общую теорию относительности в Главную теорию, и я это сделал.)
Глобальная симметрия
Rigid symmetry
Мы говорим, что симметрия физического закона является глобальной, если она требует выполнения одного и того же преобразования в каждой точке (и в любой момент времени) в пространстве-времени. Локальная симметрия, в отличие от нее, допускает преобразования, которые изменяются от точки к точке в четырехмерном пространстве-времени.
Глюон, цветной глюон
Gluon/color gluon
Глюоны – это наименьшие единицы, или кванты, глюонного флюида.
Глюонный флюид, глюонное поле
Gluon fluid/gluon field
Глюонный флюид – это активная, заполняющая пространство субстанция, ответственная за сильное взаимодействие. Глюонное поле в некоторой точке – это мера воздействия глюонного флюида в этой точке, усредненная по достаточно малому объему пространства и отрезку времени.
Гравитация
Gravity
Пока она действует между элементарными частицами, гравитация является гораздо более слабым взаимодействием по сравнению с тремя остальными взаимодействиями Главной теории. Однако остальные взаимодействия реагируют на заряды, которые могут иметь разные знаки, и поэтому имеют склонность взаимно уничтожаться, когда рядом оказывается множество частиц. Гравитация же реагирует главным образом на энергию и скорее приобретает бо?льшую силу, когда множество частиц оказывается рядом. В небесной механике гравитация является преобладающим взаимодействием.
Практически при любых обстоятельствах гравитация приводит к притяжению между телами. Темная энергия в этом смысле исключительна. В примечаниях в конце книги я предлагаю две ссылки на источники, в которых вы сможете найти больше информации по этой теме. Здесь я просто упомяну три следствия для настоящего, будущего и прошлого Вселенной в целом.
• В настоящее время гравитация обычного вещества вместе с темной материей преобладает над гравитационным влиянием темной энергии в нашем ближайшем окружении вплоть до масштабов нашей Галактики и немного за ее пределами. Однако на космологических масштабах обычное вещество и темная материя распределены неоднородно, в то время как темная энергия, хотя и имеет гораздо меньшую плотность в нашем ближайшем окружении, вездесуща, и ее влияние накапливается. В результате гравитация темной энергии, которая по существу является гравитацией отталкивания, играет преобладающую роль в эволюции Вселенной в целом. Расширение Вселенной, которое должно было бы замедляться гравитационным притяжением, на деле ускоряется.
• Прямая экстраполяция современной космологии на далекое будущее предполагает, что через сотни миллиардов лет наша Галактика, слившись с галактикой Андромеды и, возможно, с несколькими другими близлежащими карликовыми галактиками, образует изолированный остров, а всё остальное обычное вещество с темной материей во Вселенной удалится настолько далеко и настолько быстро, что будут недоступны для наблюдения из-за ограниченной скорости света.
Конечно, это очень грубая экстраполяция, учитывая то, насколько сильно менялись взгляды ученых на космологию на гораздо меньших временных масштабах. Ведь прошло меньше ста лет с тех пор, как было открыто расширение Вселенной!
• На протяжении большей части из 13 миллиардов лет (или около того) после Большого взрыва гравитация обычной и темной материи доминировала над влиянием темной энергии даже на космологических масштабах. Однако эти виды материи «разбавлялись» расширением Вселенной, а плотность темной энергии оставалась постоянной, и (примерно) в последние два миллиарда лет последняя начала доминировать. Однако существуют веские причины подозревать, что в очень ранней истории Вселенной все было по-другому, и темная энергия играла главную роль, так что ее гравитация отталкивания привела к периоду быстрой космологической инфляции.
Ньютоновская теория гравитации была эпохальным событием в истории человеческой мысли. Предоставив точное объяснение многим аспектам движения небесных тел и основываясь на нескольких четко сформулированных математических принципах, она установила новые стандарты научной точности и амбициозности. Однако в начале XX в. теория Ньютона была вытеснена общей теорией относительности Эйнштейна, которая остается основополагающей по сей день.
Гравитон
Graviton
Гравитоны – это наименьшие единицы, или кванты, возмущений в гравитационном флюиде, также называемом метрическим флюидом. Таким образом, гравитоны для гравитации – то же самое, что фотоны для электромагнетизма. Предсказывается, что отдельные гравитоны должны крайне слабо взаимодействовать с обычным веществом, и шансы наблюдать их непосредственно как индивидуальные объекты очень малы. Гравитационные волны, которые потенциально возможно зарегистрировать, состоят из огромного количества гравитонов.
Грассмановы числа
Grassmann numbers
Эти числа удовлетворяют антисимметричному правилу умножения
xy = ?yx.
Грассмановы числа выступают в суперсимметрии в качестве координат квантовых измерений.
Графен
Graphene
Графен – это химическое вещество, состоящее целиком из углерода. В графене атомы углерода формируют двумерный лист из ядер, расположенных по образцу медовых сот. Графен имеет выдающиеся механические и электрические свойства.
Группа (преобразований), непрерывная группа, группа Ли
Group of transformations, continuous group, Lie group
Часто бывает полезно рассматривать преобразования, в результате которых некоторая структура остается в целом неизменной, или инвариантной, тогда как ее части обычно перемещаются – другими словами, преобразования симметрии или просто симметрии этой структуры – не только по отдельности, но и все вместе. Такие совокупности преобразований симметрии называются группами преобразований.
Группы преобразований бывают очень разнообразны. К примеру, некоторые позволяют плавное изменение, некоторые дискретны. (См. Непрерывная симметрия.) Но все группы объединяет несколько важных свойств:
• Мы можем комбинировать два преобразования симметрии, производя сначала одно, а затем другое. В результате такого объединенного преобразования структура также останется инвариантной, следовательно, оно тоже задает преобразование симметрии.
• Для каждого преобразования симметрии существует противоположное ему, или (как обычно говорят) обратное, преобразование. Если исходное преобразование превращает x в x', то обратное ему преобразование превращает x' в x.
• Если мы скомбинируем некоторое преобразование с обратным ему преобразованием (в любом порядке), следуя нашему первому правилу, то результатом будет тривиальное тождественное преобразование, которое «превращает» любой x в себя же.
Норвежский математик Софус Ли начиная с конца XIX в. глубоко изучал группы преобразований, которые позволяют плавное изменение и могут быть исследованы методами дифференциального и интегрального исчисления. В его честь эти группы симметрий называют группами Ли. Группы симметрий для кругов, сфер и их обобщений на случай большего числа измерений, состоящие из всех преобразований, которые мы можем получить путем комбинации вращений вокруг всех возможных осей и на все возможные углы, называются группами Ли.
Эти группы вращений, так же как и другие группы Ли, находят большое применение в современной квантовой физике. Прежде всего группы симметрий пространств свойств, основанных на различных видах зарядов, которые являются краеугольными для наших Главных теорий сильного, слабого и электромагнитного взаимодействий, являются группами Ли – так же как и более обширные группы симметрии, на которые мы рассчитываем в нашей попытке объединить эти теории. См. также Локальная симметрия.
Давление
Pressure
Это понятие возникает, когда мы обсуждаем силы применительно к непрерывным средам (в противоположность частицам). Каждая часть сплошной среды прилагает силы к ее соседним частям, действуя на разделяющих их поверхностях. (Эти поверхности вводятся как воображаемые объекты и не обязаны быть реальными границами.) Давление определяется в таких случаях как сила, действующая на единичную площадь.
Дальнодействие
Action at a distance
Дальнодействие – это особенность ньютоновской теории гравитации: тела гравитационно воздействуют на другие, даже сильно удаленные тела, мгновенно через пустое пространство. Самому Ньютону не нравилась эта особенность его теории, но математические выкладки привели его именно к этому. Успех теории Ньютона, основанной на принципе дальнодействия, был столь абсолютным, что эта идея была молчаливо принята и первыми исследователями электричества и магнетизма.
Фарадей разработал альтернативный взгляд, согласно которому электрические и магнитные силы передаются как давление посредством заполняющих пространство флюидов. Максвелл развил интуитивные догадки Фарадея математически и таким образом пришел к флюидной или, иначе, полевой теории электромагнетизма, которой мы пользуемся по сей день.
Астрология постулирует мощное дальнодействие, но, мягко выражаясь, нет никаких достоверных свидетельств ее правомерности.
Действительные числа
Real numbers
На интуитивном уровне действительные числа – это числа, которые допускают непрерывное изменение. Подобно тому, как натуральные числа естественно возникают в процессе счета предметов, действительные числа действительно возникают в процессе измерения длины.
Длины могут быть разделены на очень маленькие кусочки. Поскольку не существует очевидного предела этому процессу деления, математики предполагают в качестве рабочей гипотезы, что никакого предела нет. Как эта гипотеза отражена в числах? Поскольку каждая последующая цифра в десятичной дроби по мере движения направо отвечает все более мелкому разбиению величины, напрашивается мысль, что нам следует допустить бесконечные десятичные дроби.
Ньютон был чрезвычайно впечатлен бесконечными десятичными дробями, которые в его время были свежим изобретением. Они послужили прямым источником вдохновения для его работ с бесконечными рядами и в исчислении бесконечно малых величин:
Меня удивляет поэтому, что никто… не направил своего внимания на приложение к буквам принципов недавно открытого учения о десятичных дробях, особенно потому, что при этом открывается путь к более трудным и более важным открытиям. В самом деле, это учение о буквенных выражениях находится в таком же отношении к алгебре, как учение о десятичных дробях к обычной арифметике, и кто учитывает аналогию, существующую между десятичными числами и бесконечно продолжающимися алгебраическими выражениями, сможет тогда легко изучить сложение, вычитание, деление, умножение и извлечение корней[98].
Другими словами, Ньютон считал своим основным нововведением то, что он решился использовать вместо конкретных чисел неизвестное x алгебры в таких же разложениях, как и для десятичных дробей. Самые глубокие достижения гения часто кажутся выросшими, как в данном случае, из детской непосредственности и желания позабавиться.
«Десятичные числа, которые продолжаются бесконечно» – отличное описание действительных чисел, и оно соответствует тому, как большинство математиков и по существу все физики обычно думают о них. Но это не строгое определение. Проблема создания точного определения состоит в том, чтобы зафиксировать главную идею о том, что нечто «продолжается бесконечно», используя предложения, которые бесконечно не продолжаются. На самом деле довольно трудно дать строгое определение действительных чисел. Это удалось сделать только в конце XIX в., хотя люди использовали действительные числа в течение сотен лет до того.
В современной физике благодаря открытию атомов и странностям квантовой теории корректность гипотезы о том, что не существует предела для деления отрезка, совсем не очевидна. Однако действительные числа продолжают обеспечивать интеллектуальный материал, из которого отчеканены наши Главные теории. Почему? Это кажется очень странным, по крайней мере мне. (См., чтобы узнать об этом, Бесконечно малые.)
Динамический закон, динамическое уравнение
Dynamical law/dynamical equation
Динамические законы – это законы, которые определяют, как величины меняются во времени. Динамические законы формулируются в виде динамических уравнений.
Пример: Второй закон движения Ньютона определяет ускорение тел, которое показывает, как их скорости меняются со временем.
Контрпример: Законы сохранения, напротив, констатируют, что величины не меняются со временем.
Основные законы нашей Главной теории являются динамическими законами, но они подразумевают законы сохранения для нескольких особых величин.
Второй контрпример: в Главной теории существует некоторое число так называемых свободных параметров. Это величины, участвующие в уравнениях, чьи значения не фиксированы никаким общим принципом, но скорее берутся из эксперимента. Они молчаливо считаются постоянными во времени.
Возможный контрпример: основная идея физики аксионов состоит в том, что один из этих параметров, так называемый параметр ?, подчиняется динамическому уравнению более общей теории. В этой более общей теории «случайность» того, что наблюдаемое значение ? очень мало, становится следствием решения динамического уравнения. В целом можно надеяться, что другие свободные параметры Главной теории будут когда-нибудь определены из решений динамических уравнений в рамках более фундаментальных теорий.
(См. также начальные условия.)
Длина волны
Wavelength
Волны, которые повторяются или, как мы говорим, периодически изменяются в пространстве, особенно важны – одновременно потому, что они возникают естественным путем, и потому, что они предоставляют нам основные элементы, из которых мы можем воссоздать более сложные волновые движения, в духе Анализа и Синтеза. Чистые музыкальные тона среди звуковых волн и чистые спектральные цвета для случая электромагнитных волн являются периодическими в пространстве, так же как и во времени. (См. Тон, чистый тон.)
Расстояние между повторениями в простой волне называют ее длиной волны. Таким образом, длина волны играет ту же роль для изменения в пространстве, что и период для изменения во времени. Примеры:
• Самые низкие тона, которые люди могут слышать, имеют длины волн (в воздухе) около 10 метров, в то время как самые высокие тона, которые люди могут услышать, имеют длины волн (в воздухе) приблизительно один сантиметр. Не случайно размеры большинства музыкальных инструментов сопоставимы со средней длиной волны в этом промежутке, ведь они предназначены для воспроизведения звуковых волн, которые люди могут услышать. Басовые трубы духовых органов на одном краю и флейты-пикколо на другом лежат на границах этого диапазона. Свистки для собак находятся слегка за его пределами!
• Спектральные цвета, которые могут видеть люди, имеют длины волн в пределах приблизительно от 400 нанометров (что эквивалентно 4 ? 10–7 метрам, или 0,4 микрона) на синем краю, до 700 нанометров на красном краю спектра. Этим маленьким длинам волн сложно поставить в соответствие какие-либо механические приспособления. «Музыкальные инструменты» для света – это атомы и молекулы.
Конечно, можно расширить двери восприятия[99] искусственно, с помощью соответствующих приборов.
Дополнительный, дополнительность
Complementary/complementarity
Мы говорим, что два подхода к одной и той же задаче дополнительны (или комплементарны), если каждый из них правомерен и логичен сам по себе, но они не могут применяться одновременно, поскольку мешают друг другу. Это распространенная ситуация в квантовой механике. Например, можно выбрать, измерять положение частицы в пространстве или ее импульс – но невозможно измерять обе эти характеристики одновременно, так как эти измерения мешают друг другу. Отчасти вдохновленный подобными примерами, но также и своим обширным жизненным опытом, Нильс Бор предположил, что будет разумно применять понятие дополнительности гораздо более широко в качестве оригинального метода решения трудных задач и преодоления очевидных противоречий. Такое более широкое понятие дополнительности, которое кажется мне полезным и раскрепощающим, лучше всего объяснить на примерах. Вы найдете несколько таких примеров в нашем заключительном постскриптуме «Красивый ответ?».
Закон Ампера (Закон Ампера – Максвелла)
Amp?re's law/Amp?re – Maxwell's law
Закон Ампера сейчас считается частью одного из уравнений Максвелла, хотя исторически он был открыт раньше. Закон Ампера в его оригинальной формулировке гласит, что циркуляция магнитного поля по замкнутому контуру равна потоку электрического тока через любую поверхность, ограниченную этим контуром. Чтобы разобраться в этом, ознакомьтесь со статьями Циркуляция, Поток и Ток. Также вам будет полезна цветная вклейка N.
Максвелл, руководствуясь соображениями математической логики и красоты, видоизменил закон Ампера, добавив в него еще один член[100]. Согласно полному закону Ампера – Максвелла циркуляция магнитного поля по замкнутому контуру равна потоку электрического тока через любую поверхность, ограниченную этим контуром, плюс скорость изменения потока электрического поля через эту поверхность.
Новое слагаемое Максвелла в каком-то смысле можно назвать дуальным к закону Фарадея. Закон Фарадея гласит, что изменяющееся магнитное поле может создавать электрическое поле, тогда как поправка Максвелла означает, что изменяющееся электрическое поле может создавать магнитное поле.
Закон сохранения, сохраняющаяся величина
Conservation law/conserved quality
Мы говорим, что некая величина сохраняется, если ее значение не меняется со временем. Закон сохранения – это утверждение о том, что некоторая величина сохраняется. Многие из наших важнейших озарений об устройстве мира могут быть выражены в виде законов сохранения. Эмми Нётер доказала важную теорему, подробно описанную в тексте книги, которая проводит тесную связь между законами сохранения и наличием симметрии, или инвариантности.
Примеры: cохранение энергии, сохранение импульса, сохранение момента импульса и сохранение электрического заряда – это законы сохранения; энергия, импульс, момент импульса и электрический заряд – это сохраняющиеся величины.
Фраза «сохранение энергии» заслуживает особого внимания, поскольку ее использование в науке отличается от общепринятого. Нам часто советуют сохранять – беречь – энергию, например, выключая электрический свет ночью, или снижая температуру на наших обогревателях, или гуляя пешком вместо того, чтобы использовать машину. Но действительно ли миру нужна наша помощь, чтобы его основные законы соблюдались? Смысл в том, что, когда нас побуждают сохранять энергию, на самом деле нас просят удерживать энергию в таких формах, которые могут быть использованы позже для выполнения полезной работы, и не позволять ей переходить в бесполезные (тепло) или вредные (химические реакции, в которых выделяются токсины) формы. Понятие свободной энергии в термодинамике отражает некоторые из этих различий. Свободная энергия, которая является обобщенно-полезным видом энергии, не сохраняется. Она имеет тенденцию уменьшаться, или, как часто говорят, рассеиваться, со временем.
Закон Фарадея
Faraday's law
Этот закон утверждает, что циркуляция электрического поля по замкнутому контуру равна скорости изменения потока магнитного поля через любую поверхность, натянутую на этот контур, взятой со знаком минус. Закон Фарадея увековечен в одном из уравнений Максвелла.
Измерение и размерность
Dimension
Интуитивно, измерение – это возможное направление движения. Так, мы говорим, что прямая или кривая имеет одно измерение. Плоскость или поверхность имеет два измерения, поскольку требует движения в двух независимых направлениях – например, мы можем назвать их «горизонтальное» и «вертикальное», или «север-юг» и «запад-восток», – чтобы достичь любой точки из любой другой. Обычное пространство, в котором мы живем, или твердое тело имеет три измерения.
Более гибкое понятие «пространства» и измерения возникает естественным образом при введении координат. Здесь вам следует обратиться к статье о координатах, где обсуждается это понятие. Размерность[101] пространства, в котором введены координаты, равна необходимому для него числу координат. Это понятие в приложении к простым, гладким геометрическим объектам согласуется с предыдущей интуитивной идеей.
Математики обобщили эти более или менее интуитивные понятия измерений многими способами. Два примечательных обобщения – это комплексные измерения и дробные, или фрактальные, размерности. Комплексные измерения добавляют больше координат, но таких координат, которые являются комплексными числами. Дробные размерности могут возникнуть при рассмотрении объектов, содержащих очень богатую локальную структуру и очень далеких от понятия гладкости (см. Фракталы). В последние годы в связи с суперсимметрией физики ввели понятие квантовых измерений. Координаты квантовых измерений являются грассмановыми числами.
Есть и еще одно, совершенно отличное использование слова «размерность» в науке. В этом употреблении мы говорим о единицах, в которых измеряется какая-либо величина, как о ее размерности. В этом смысле площадь имеет размерность длины в квадрате, тогда как у скорости размерность длины, поделенной на время, у силы – размерность массы, умноженной на длину и поделенной на квадрат времени, и т. д. Чтобы не допустить возможной путаницы, я избегал использования слова «размерность» в этом смысле.
Изотоп
Isotope
Ядра с одинаковым числом протонов, но с различным числом нейтронов называются изотопами. Ядра, которые являются изотопами, имеют одну и ту же величину электрического заряда, что приводит к практически одинаковому химическому поведению, хотя они значительно отличаются по массе.
Импульс
Momentum
Импульс вместе с энергией и моментом импульса является одной из выдающихся сохраняющихся величин классической физики. Каждая из них также развилась в основополагающий столп современной физики.
Импульс тела является мерой его количества движения. Количественно он равен массе тела, умноженной на его скорость. (Это нерелятивистская версия, верная для небольших скоростей. Специальная теория относительности приводит к родственной, но более сложной формуле.)
У импульса есть направление, так же как и величина. Таким образом, это векторная величина.
Импульс системы тел равен сумме импульсов тел по отдельности.
Импульс сохраняется в самых разнообразных обстоятельствах. Этот результат лучше всего понятен в рамках общей теоремы Нётер, которая связывает законы сохранения с симметрией. В этой парадигме сохранение импульса отражает симметрию (инвариантность) физических законов относительно трансляции (сдвига) в пространстве – т. е. относительно преобразований, которые перемещают все в рассматриваемой системе на одинаковое расстояние. Другими словами, мы имеем сохранение импульса, если законы, управляющие нашей системой, не зависят ни от какого внешне заданного, фиксированного положения в пространстве.
В квантовом мире импульс остается правомерным понятием и приобретает дополнительные, очень изысканные и красивые свойства.
Инвариантность
Invariance
Мы называем что-то инвариантным относительно некоторого преобразования, если такое преобразование не изменяет его.
Примеры:
• Расстояние между объектами инвариантно, если вы перемещаете все объекты в одном и том же направлении на одинаковое расстояние (инвариантность расстояния относительно трансляции в пространстве).
• Форма круга является инвариантной, если вы поворачиваете его вокруг его центра (инвариантность круга относительно вращения).
• Скорость, с которой распространяется луч света, является инвариантной, если вы движетесь с любой постоянной скоростью. Таким образом, мы говорим, что скорость света является инвариантной относительно преобразований Галилея или, что эквивалентно, относительно бустов, которые преобразуют координаты между системами отсчета, связанными с платформами, движущимися с различными скоростями.
Третий из этих примеров описывает ключевое положение специальной теории относительности Эйнштейна.
Интенсивность (света)
Intensity of light
Интенсивность света – точное понятие, которое соответствует воспринимаемой степени яркости. Интенсивность луча света, падающего на поверхность, – это количество энергии, которую луч доставляет на эту поверхность, в единицу времени и на единичную площадь[102]. Это определение позволяет нам обобщить понятие интенсивности на все части электромагнитного спектра, такие как радиоволны, инфракрасное излучение, ультрафиолетовое излучение и рентгеновские лучи.
Исчисление
Calculus
Русским словом исчисление принято переводить английское calculus, которое, в свою очередь, происходит от латинского слова, обозначающего камень или гальку. Его современное использование в математике восходит к операции счета или учета расходов и доходов с помощью счетных камешков (так же как многие люди делают это, даже в наши дни, с помощью счет). Мы видим след этого происхождения в общем английском термине «calculation», который используется для обозначения множества различных методов и операций для обработки информации, и в русской «калькуляции» с несколько более узким значением.
Математика признает несколько видов исчисления (например, исчисление высказываний, лямбда-исчисление, вариационное исчисление). Но один конкретный метод обработки математических данных настолько важен и произвел такой эффект на ученые умы, что когда люди произносят «calculus» без каких-либо пояснений, то подразумевается именно он – математический анализ.
В этом понимании «calculus» – это метод Анализа и Синтеза в применении к изучению гладко меняющихся процессов, или функций. Две ветви математического анализа, дифференциальное и интегральное исчисление, отражают этот метод. Дифференциальное исчисление снабжает нас методами для анализа поведения на очень малых отрезках, тогда как интегральное исчисление предоставляет методы для синтеза такой локальной информации в глобальное понимание.
Выдающимся приложением математического анализа, которое имел в виду Ньютон, развивая этот предмет, является описание движения. Можно ввести такие понятия, как скорость и ускорение, для того, чтобы охарактеризовать движение на очень коротких отрезках времени (дифференциальное исчисление), или, наоборот, можно использовать информацию о скорости и ускорении, чтобы вычислять орбиты (интегральное исчисление). В классической механике законы о силах предоставляют информацию об ускорении тела. Важной задачей в классической физике является задача о том, как использовать эту информацию: понять, как движется тело в ответ на известное ускорение. Это задача интегрального исчисления: понять что-то большее из знания малого.
Калибровочная симметрия
Gauge symmetry
Это еще один термин для локальной симметрии.
Калибровочная частица
Gauge particle
Чтобы обеспечить выполнение локальной (калибровочной) симметрии, необходимо ввести соответствующие флюиды, чьи свойства специально подобраны для этой цели. В Главной теории по этой причине появились гравитационный, сильный, слабый и электромагнитный флюиды. Наименьшие единицы, или кванты, этих флюидов – гравитоны, цветные глюоны, виконы и фотоны – по этой причине называются калибровочными частицами. Этот термин звучит обыденно, однако за ним скрывается глубокий и красивый факт: частицы, с помощью которых передаются фундаментальные взаимодействия Природы, являются воплощениями симметрии.
Качественный и количественный
Qualitative/quantitative
Мы говорим, что понятие, теория, представление или измерение являются количественными, когда они выражаются числами. В противном случае они качественные. «Числа», используемые в количественном описании, могут быть натуральными числами, действительными числами, комплексными числами или какими-то другими, в зависимости от задачи.
Мы также говорим о полуколичественных концепциях, теориях, представлениях или измерениях, когда они выражены с использованием чисел, но не вполне точно или последовательно. Мы можем обнаружить, что различные ученые-практики, используя ту же самую полуколичественную физическую теорию, выводят из нее различные следствия в зависимости от того, каким образом они дополняют плохо определенные части теории.
Слово «качественный» может также использоваться для усиления следующим образом. Говоря, что идея или явление качественно новы, мы подразумеваем, что это не просто дальнейшая разработка или углубление того, что было известно прежде, а нечто принципиально другое, так что старое и новое нельзя сравнивать количественно. Например, волновые функции квантовой теории качественно отличаются от орбит классической физики, чье место они заняли теперь.
Квант (единица материи), кванты
Quantum (unit of matter)/quanta
Объекты, которые мы обычно называем элементарными частицами, считаются, согласно нашей Главной теории, возмущениями в квантовых флюидах. Таким образом, фотоны – это возмущения в электромагнитном флюиде, электроны – возмущения в электронном флюиде, глюоны – возмущения в глюонном флюиде, частицы Хиггса – возмущения в флюиде Хиггса и т. д. Если мы рассматриваем движение этих флюидов согласно правилам классической физики, мы видим, что их энергия может принимать непрерывный ряд значений. Но когда мы рассматриваем их согласно правилам квантовой теории, мы обнаруживаем, что разрешенные возмущения существуют в виде неделимых единиц, а именно в виде чего-то, что мы признаем элементарными частицами!
См. главным образом статью о Фотоне, чтобы узнать больше о кванте электромагнитного поля – исходных «квантах света» Планка и Эйнштейна.
Квантование
Quantization
Этот термин используется в трех различных смыслах: в общем, в конкретном специальном значении и как элемент жаргона.
Общий смысл: когда мы отображаем, или, как мы говорим, проецируем непрерывную величину на набор дискретных значений, мы говорим, что подвергли эту величину квантованию. Другими словами, процесс квантования превращает аналоговую величину в ее цифровое представление. Квантование в этом смысле является самой обычной практикой в современной инженерии и обработке информации, потому что цифровые величины легче передать и хранить их точные значения, чем аналоговые величины. (См. Аналоговый и Цифровой, чтобы узнать больше.) За некоторыми, очень специальными исключениями современные компьютеры работают лишь с цифровой информацией, и поэтому значения аналоговых сигналов, таких как интенсивность света, квантуются еще до того, как они будут введены. Эта операция называется квантованием.
Важный результат квантовой механики состоит в том, что она квантует (в вышеуказанном смысле) многие величины, которые в классической физике были непрерывны. (За этим стоит Природа, или Творец, а не какой-то человек-инженер!) Примеры квантуемых в узком смысле величин и объектов:
• Энергия в электромагнитной волне. См. Фотон.
• Энергия в атоме. Согласно классической механике отрицательно заряженный электрон может двигаться вокруг положительно заряженного протона по многим слегка отличающимся орбитам, что позволяет ему иметь непрерывный диапазон энергий. В квантовой механике разрешенные орбиты отличаются дискретно, т. е. являются квантованными, и, следовательно, разрешенные энергии тоже. (См. Стационарное состояние, Спектры (атомный, молекулярный и прочие) и подробное обсуждение с рисунками в главе «Квантовая красота I».)
• Элементарные частицы как таковые. См. Квант (единица материи), кванты.
Жаргон: физики часто называют процедуру применения квантовой механики к физической системе «квантованием» этой системы. Это существенно иное использование термина, которое может вызвать путаницу. Профессионалы в своих беседах могут использовать его без опаски, но в этой книге я избегаю такого использования.
Квантовая теория, квантовая механика
Quantum theory/quantum mechanics
Великое открытие начала XX в. состоит в том, что законы физики, используемые для описания больших тел и воплощенные в ньютоновской механике и электродинамике Максвелла, не подходят для того, чтобы описать атомы и их ядра. Чтобы описать поведение материи на атомных и субатомных масштабах, оказалось необходимым не просто дополнить то, что было известно раньше, а сконструировать радикально иную систему взглядов, в которой многие идеи, которые считались давно устоявшимися, пришлось отбросить. Обобщающий термин квантовая теория, или квантовая механика, относится к этой новой платформе. Она была сформирована в общих чертах к концу 1930-х гг. С тех пор наши возможности справиться с математическими вызовами, которые бросает нам квантовая теория, несравнимо улучшились (см. Перенормировка), и мы пришли благодаря нашим Главным теориям к значительному детальному пониманию основных взаимодействий Природы. Но эти разработки имели место в рамках квантовой теории.
Многие физические теории могут быть сформулированы в виде достаточно конкретных предположений о физическом мире. Специальная теория относительности, например, является по сути результатом объединения двух предположений: предположения о галилеевой симметрии и предположения об инвариантности скорости света. Каждая из наших Главных теорий на деле является предположением о наличии локальной симметрии – вместе со специфическими подробностями того, как связанные с ней преобразования симметрии воздействуют на пространство-время и материю.
Квантовая теория в ее современном понимании устроена иначе. Квантовая теория не является какой-то определенной гипотезой, а представляет собой сеть тесно связанных и переплетающихся идей. Я вовсе не хочу внушить вам, что квантовая теория определена нечетко – это не так. За редкими и, как правило, временными исключениями все сведущие ученые, занимающиеся квантовой механикой, столкнувшись с любой конкретной физической проблемой, придут к согласию о том, как следует подходить к этой проблеме, используя квантовую теорию. Но я сомневаюсь, что многие из них (а может, и вовсе никто) смогли бы точно сказать, какие предположения они сделали, чтобы к этому прийти.
Хотя точное определение дать тяжело, но все же возможно (и полезно для ясности) указать здесь несколько качественно новых тем, которые квантовая теория привносит в наше описание материального мира:
• В описании материи элементарные объекты – это не частицы, занимающие положение в пространстве, и даже не поля (наподобие электрических полей), которые заполняют все пространство скалярными числами или векторами, а волновые функции. Волновые функции приписывают комплексные числа, называемые амплитудами, возможным конфигурациям объекта, который они описывают.
Таким образом, волновая функция отдельной частицы приписывает амплитуду всем возможным положениям частицы – в каждой точке пространства. Волновая функция пары частиц приписывает амплитуду парам точек в пространстве, т. е. точкам в шестимерном пространстве парных положений. Волновая функция электрического поля – это объект ошеломляющей необъятности. Поскольку она приписывает амплитуду любому возможному значению электрического поля в целом, волновая функция электрического поля – это функция от (векторных) функций!
• На любой допустимый физический вопрос о физической системе можно ответить, посмотрев на ее волновую функцию. Но связь между вопросом и ответом не так уж проста. И способ, которым волновые функции отвечают на вопросы, и ответы, которые они дают, имеют удивительные, если не сказать таинственные свойства.
Чтобы быть конкретнее, давайте сначала рассмотрим это в относительно простом контексте отдельной частицы. (Здесь мы частично резюмируем обсуждение из основного текста.) Чтобы задать вопросы, мы должны выполнить определенные эксперименты, которые исследуют волновую функцию различными способами. Мы можем выполнить, например, эксперименты, которые измеряют положение частицы, или эксперименты, которые измеряют импульс частицы. Эти эксперименты отвечают на вопросы «Где находится частица?», «Как быстро она перемещается?».
Как волновая функция отвечает на эти вопросы? Сначала она делает некоторую обработку и затем выдает вам вероятности.
Что касается вопроса о положении, обработка довольно проста. Мы берем значение, или амплитуду, волновой функции – комплексное число, не забывайте – и возводим ее модуль в квадрат. Для каждого возможного положения это дает нам положительное число или ноль. Это число – вероятность найти частицу в данной точке пространства. (Строго говоря, это плотность вероятности, но не будем умножать сложности.)
Что касается вопроса об импульсе, процесс обработки значительно более сложен. Чтобы узнать вероятность наблюдения некоторого импульса, вы должны сначала выполнить взвешенное усреднение волновой функции – точный способ выполнить взвешивание зависит от того, каким импульсом вы интересуетесь, – а затем возвести в квадрат это среднее значение.
Здесь три важных момента:
• Вы получаете вероятности, а не определенные ответы.
• Вы не получаете доступ к самой волновой функции, вы только мельком видите ее обработанные версии.
• Получение ответов на различные вопросы может потребовать обработки волновой функции разными способами.
Каждый из этих трех моментов чреват серьезными проблемами.
Первый ставит проблему детерминизма. Действительно ли вычисление вероятностей – это лучшее, что мы можем сделать?
Второй ставит проблему многих миров. Что описывает полная волновая функция, когда мы не делаем выборку? Представляет ли она гигантское расширение действительности или это только мысленный инструмент, не более реальный, чем сон?
Третий поднимает вопрос о дополнительности. Получение ответов на различные вопросы может требовать обработки волновой функции различными способами, которые взаимно несовместимы. В этом случае, согласно квантовой теории, невозможно ответить на оба вопроса одновременно. Вы не можете сделать это, даже если каждый вопрос в отдельности будет совершенно законным и будет иметь содержательный ответ. Именно эта ситуация возникает для нашего вопроса о положении и вопроса об импульсе, это называется принципом неопределенности Гейзенберга: вы не можете измерить и положение, и импульс частицы одновременно. Если бы кто-то придумал, как сделать это экспериментально, он бы опроверг квантовую теорию, поскольку квантовая теория говорит, что это невозможно. Эйнштейн неоднократно пытался изобрести эксперименты такого рода, но ему это так и не удалось, и в конечном счете он сдался.
Каждая из этих проблем пленяет воображение, и первым двум из них уделили много внимания. Однако мне кажется, что третья особенно хорошо обоснована и значима. Дополнительность как свойство физической реальности и урок мудрости занимает в нашей медитации важное место.
Хотя я объяснил эти проблемы на примере отдельных частиц, все они проявляются в полной мере и тогда, когда мы задаемся вопросами о более сложных системах.
• Поскольку волновая функция дает нам вероятности, а не точные ответы, мы получим различные ответы, если будем много раз задавать тот же вопрос одной и той же волновой функции. Это тесно связано с той интуитивной моделью, которая мне очень нравится и к которой я часто прибегаю, суть ее в том, что квантовые объекты проявляют спонтанную активность. См. Квантовые флуктуации.
• Многие непрерывные согласно классической физике величины становятся дискретными в квантовой теории. См. Фотон и Спектры.
• И последнее, но никак не менее важное: хотя квантовая теория обычно приводит к вероятностным ответам, она в то же время делает много предсказаний, которые являются совершенно определенными. Например, квантовая механика лежит в основе теорий, предсказывающих спектр водорода, прочность и электрическую проводимость нанотрубок, массы и свойства адронов – причем с удивительной точностью. Все это точно определенные значения, не вероятности. Эти блестящие результаты являются яркими страницами в новейшей истории нашего Вопроса, как это обсуждается в главах «Квантовая красота I», «Квантовая красота II» и «Квантовая красота III».
Квантовая точка
Quantum dot
Физики разрабатывают усовершенствованные методики создания очень маленьких материальных структур со стороной всего в несколько атомов. Эти структуры называют квантовыми точками. Квантовые точки – это, по сути, молекулы, сделанные вручную.
Квантовая хромодинамика (КХД)
Quantum chromodynamics (QCD)
Квантовая хромодинамика, или КХД, является нашей Главной теорией сильного взаимодействия.
КХД привносит много новых идей в описание Природы, включая кварки, цветовой заряд, цветные глюоны, асимптотическую свободу, конфайнмент и струи.
КХД в своей сфере действия дает четкий положительный ответ на волнующий нас Вопрос: воплощает ли мир красивые идеи? А именно КХД воплощает красивый принцип локальной симметрии в необыкновенно богатом контексте пространства свойств сильного цветового заряда.
Квантовая электродинамика (КЭД)
Quantum electrodynamics (QED)
Квантовая электродинамика, или КЭД, является нашей Главной теорией электромагнетизма.
КЭД основана на уравнениях Максвелла в неизменной форме, но интерпретируемых в соответствии с правилами квантовой теории. Это значит, что возмущения в электромагнитном флюиде возникают в виде дискретных единиц, или квантов, – фотонов, а во флюиде наблюдается также самопроизвольная активность – квантовые флуктуации.
Квантовая электродинамика предоставляет твердый и законченный фундамент для «всей химии и большей части физики», как сказал Поль Дирак.
Квантовые измерения
Quantum dimension
Квантовые измерения – это измерения, координаты которых являются грассмановыми числами. Квантовые измерения – это душа суперсимметрии.
Квантовые флуктуации, виртуальные частицы, поляризация вакуума и нулевые колебания
Quantum fluctuation/virtual particle/vacuum polarization/zero-point motion
В теории квантовых флюидов, которая лежит в основе нашего наиболее глубокого понимания Природы, мы пришли к новому взгляду на частицы. Они являются минимальными возмущениями, или квантами, в квантовых флюидах. Таким образом, фотоны – это кванты электромагнитного флюида, электроны – кванты электронного флюида и т. д.
В этих флюидах, однако, заключено нечто большее, чем частицы, которым они служат основой, так же как и вода есть нечто большее, чем волны на ее поверхности. В частности, у флюидов есть самопроизвольная активность: квантовые флуктуации. Поскольку самопроизвольная активность и возмущения в квантовом флюиде, которые мы распознаем как частицы, тесно связаны – это два свойства одного и того же флюида, – принято говорить, что эта спонтанная активность состоит из виртуальных частиц. Таким образом, виртуальные частицы – игра нашего собственного ума, чтобы представить активность в виде объектов. Это воображаемые объекты.
На спонтанную активность квантового флюида может влиять присутствие частиц, и наоборот. Таким образом, свойства частиц меняются из-за обратной связи с квантовыми флюидами: присутствие частицы влияет на активность флюида, а эта активность в свою очередь влияет на частицу. Такую петлю обратной связи называют поляризацией вакуума. Мы можем представить себе простую и понятную картину этого эффекта, используя понятие виртуальных частиц. Виртуальные частицы образуют газ, заполняющий пространство, и свойства любой реальной частицы меняются за счет соударений с частицами этого газа.
Нулевые колебания – еще одно название спонтанной активности квантовых флюидов. Фраза «нулевые колебания» подчеркивает, что такая активность, или движение, присутствует даже тогда, когда устранены все источники энергии, т. е. даже при абсолютном нуле температуры.
Частицы, будучи возмущениями во флюидах, проявляющих спонтанную активность, наследуют эту спонтанность. У них тоже есть нулевые колебания, и они осложняют эксперименты, разработанные для обнаружения малых эффектов, таких как гравитационные волны или космическое фоновое аксионное излучение, через их влияние на обычное вещество: появляется источник фонового «шума», как будто наш измерительный прибор «покачивается» и «трясется»[103]. Этого квантового шума, возникающего из-за фундаментальных физических процессов, невозможно избежать путем охлаждения нашего измерительного прибора до низких температур или его изоляции. Лучшее, что можно сделать, – это понять, с чем мы имеем дело, и попытаться как-то обойти это затруднение.
Влияние квантовых флуктуаций на наблюдаемое поведение частиц, т. е. поляризация вакуума, является основным пунктом в нашем понимании глубинных законов Природы. Асимптотическая свобода – это следствие поляризации вакуума, и количественные аспекты объединения взаимодействий также основаны на ней. Большая часть глав «Квантовая красота III» и «Квантовая красота IV» посвящена этим идеям.
См. также Перенормировка (ренормализационная группа).
Квантовый переход, квантовый скачок
Quantum jump/quantum leap
См. Стационарное состояние, где эти понятия обсуждаются в своем естественном контексте. Здесь я отмечу только, что квантовые скачки – это на самом деле очень маленькие прыжки. Таким образом, если кто-то хвастается тем, что совершил «квантовый скачок в мышлении», и знает, о чем он говорит, то его заявление в действительности очень скромно.
Квантовый флюид, квантовое поле
Quantum fluid/quantum field
В квантовой теории свойства флюидов или полей существенно отличаются от свойств сред, с которыми мы встречаемся в доквантовой, классической физике. Наиболее значительные отличия таковы:
• Квантовые флюиды проявляют спонтанную активность даже в отсутствии внешнего влияния или «причин». См. Квантовые флуктуации, виртуальная частица, поляризация вакуума и нулевые колебания.
• Возмущения или возбуждения в квантовых флюидах не могут быть сколь угодно малыми, а возникают в виде минимальных единиц – квантов.
Квантовые флюиды – это основные компоненты, из которых строится наша Главная теория.
Кварк
Quark
Понятие кварков было независимо введено Мюрреем Гелл-Манном и Джорджем Цвейгом в 1964 г. Они представили основные компоненты модели кварков, которая внесла порядок в «зоологию» адронов. Непрерывная нить исследований соединяет их пионерскую работу с современными представлениями о кварках, которые стоят на почетном месте среди частиц вещества в нашей Главной теории.
Кварковая модель
Quark model
Кварковая модель – это полуколичественная модель адронов. Исторически она сыграла важную роль в упорядочивании данных о сильном взаимодействии. Чтобы узнать больше о кварковой модели, см. главу «Квантовая красота III», часть 2.
Кинетическая энергия.
См. Энергия.
Колебание
Oscillation
Мы называем физический процесс, который проходит через много циклов повторяющихся состояний, причем через фиксированный интервал времени, колебанием. Вибрации после щипка струн или удара по камертону, знакомые из музыки, являются примерами колебаний.
Комплексное измерение
Complex dimension
Обычные («вещественные») измерения естественным образом описываются с помощью чисел – координат, – которые являются действительными числами. К примеру, позиция точки на экране компьютера задается двумя действительными координатами, обозначающими ее положение по вертикали и по горизонтали, в то время как точка в обычном пространстве задается тремя координатами. Во многих математических и физических контекстах бывает удобно рассматривать пространства, в которых координаты задаются комплексными числами. В этом случае мы говорим, что у нас имеется комплексное пространство и что необходимое число координат равно числу комплексных измерений в этом пространстве. Поскольку комплексное число может быть задано двумя действительными числами – а именно величинами его действительной и мнимой частей, – комплексное пространство можно также рассматривать как вещественное пространство (с дополнительной структурой). Если рассматривать его таким образом, то число его вещественных измерений будет равно удвоенному числу его комплексных измерений.
Комплексные числа
Complex numbers
Мнимая единица, обозначаемая i, это число, которое в результате умножения на себя дает ?1. Или, в виде уравнения, i?= ?1. Комплексные числа – это числа вида z = x + iy, где x и y – действительные числа; x называется действительной частью z, а y – мнимой частью.
Комплексные числа можно складывать, вычитать, умножать и делить, подобно тому, как это делается с действительными числами.
Комплексные числа были введены в математику, чтобы уравнения общего вида, включающие суммирование и возведение в степень, – так называемые полиномиальные уравнения – могли иметь решения. Так, например, уравнение z? = ?4 не имеет решения в действительных числах, но оно имеет решение z = 2i (и z = ?2i). Можно доказать, что комплексные числа в том виде, как мы их определили, полностью пригодны для этой задачи. (Этот результат, так называемая основная теорема алгебры, отнюдь не очевидна и ее доказательство было важным событием в математике.)
Как подсказывает название «мнимые» (и его явное противопоставление термину «действительные»), математики с большим трудом примирились с таким видом чисел. Их «существование» почему-то казалось сомнительным. Лишь несколько смельчаков мудро вняли совету отца Джима Малли – «Более достойно благословения просить прощения, чем разрешения» – и использовали их. Привычка и дальнейшие успехи в конце концов привели к тому, что комплексные числа стали пользоваться большим уважением. Математика XIX в. в большой степени была исследованием ослепительных перспектив того, что комплексные числа могут дать исчислению и геометрии.
В XX в. способ введения новых видов объектов путем cоставления списка их желательных свойств и объявления, что такие объекты существуют, – способ, который был так успешен с комплексными числами, стал обычной рабочей процедурой. Эмми Нётер сыграла большую роль в развитии такого образа мыслей. Если бы Платон узнал о таких изменениях, он, возможно, почувствовал бы себя оправданным, учитывая, что математики полностью приняли его философию и познали радость Идеалов.
(Позволю себе небольшое отступление, которое стоит читать как поэзию. Действительно, идеалы, которые так и называют, являются важным классом математических объектов. Возможно, произведением искусства в чистой математике, сравнимым по глубине и значению с теоремой сохранения, которой мы пели хвалу в основном тексте, является понятие нётерова кольца. Что такое нётерово кольцо? Это кольцо, в котором любая цепь возрастающих идеалов в итоге заканчивается. Конец отступления.)
Другой полезный способ представления комплексного числа заключается в том, чтобы записать его как z = r cos q + ir sin q, где r – это положительное действительное число либо ноль, а q – угол; r называется модулем комплексного числа, а q называется его фазой[104]. Таким образом, либо (x, y), либо (r, q) могут служить координатами комплексных чисел.
В квантовой теории комплексные числа встречаются повсеместно.
Комплексные числа – это божественные числа.
Конфайнмент
Confinement
Основные ингредиенты квантовой хромодинамики (КХД), нашей теории сильного взаимодействия, – это кварки и глюоны. Есть огромное количество доказательств (частично описанных в главе «Квантовая красота III») того, что эта теория верна. Но ни кварки, ни глюоны не наблюдаются в виде отдельных частиц. Они обнаруживаются только как составные части более сложных объектов – адронов. Описывая эту ситуацию, мы говорим о конфайнменте (удержании) кварков и глюонов.
Мы можем представить себе попытку освободить («вырвать») кварк из протона либо постепенно, разделяя протон на части пинцетом, либо облучая протон частицами с высокой энергией и разбивая его (протон) таким образом на составные части. Каждая из этих попыток проваливается интересным – и я бы сказал, красивым – образом.
Если мы будем делать это медленно, мы обнаружим, что существует непреодолимая сила, которая тянет кварк обратно внутрь.
Если мы сделаем это быстро, мы получим струи.
Чтобы узнать об этом больше, см. «Квантовая красота III», особенно вторую часть.
Координаты
Coordinates
Когда мы используем наборы чисел для задания точек в пространстве, мы называем эти числа координатами.
Введение координат связывает понятия счета и количества, которые относятся к работе левого полушария мозга, с понятиями формы и очертаний, которые обрабатываются в правом полушарии. Хотя лежащая в основе этого психология туманна в деталях, нет сомнений, что метод координат помогает разнообразным модулям нашего мозга общаться друг с другом и объединять усилия.
Самый простой, самый базовый пример использования координат – описание прямой с использованием действительных чисел. Чтобы сделать это, нам нужно выполнить три шага:
• Выбрать точку на прямой. (Подойдет любая точка.) Эта выбранная точка будет называться началом координат.
• Выбрать длину. (Можно использовать метры, сантиметры, дюймы, футы, версты, световые годы и т. д.) Эта выбранная длина называется единицей длины. Для определенности выберем метры.
• Выбрать направление на прямой. (Есть всего две возможности.) Это выбранное направление называется положительным направлением.
А теперь, чтобы определить координату точки P, мы измеряем расстояние в метрах между точкой P и началом координат. Это положительное действительное число. Если направление от начала координат до P – положительное направление, то это число и есть координата точки P. Если направление от начала координат до точки P противоположно положительному направлению, то координатой точки P является это число со знаком минус. Координата самого начала координат – это ноль.
Таким способом мы устанавливаем точное соответствие между действительными числами и точками на прямой: каждая точка имеет единственную действительную координату и каждое действительное число – координата единственной точки.
Похожим образом мы можем задать точки на плоскости, используя пары действительных чисел, или точки в модели трехмерного пространства, используя тройки действительных чисел. Мы называем эти числа координатами точек. Также мы можем использовать комплексные числа в качестве координат для описания плоскости. Действительно, представление z = x + iy задает два действительных числа x, y – и, следовательно, точку на плоскости – с помощью одного комплексного числа z.
Конечно, если у нас есть только отрезок прямой, мы все равно можем использовать действительные числа, чтобы задать его точки, но не все действительные числа будут на нем представлены, аналогично и для других случаев.
Опыт построения карт демонстрирует нам, как с помощью подходящей проекции мы можем представить кривые поверхности на плоскости (например, на плоском листе бумаги). Таким образом мы можем использовать координаты для задания точек на искривленных поверхностях.
Базовая идея координат допускает многие вариации и обобщения:
• Мы можем использовать больше чисел! Хотя нам сложно представить больше трех измерений, работать с пятерками или еще большими наборами действительных чисел не сильно сложнее, чем работать с тройками. Таким образом, пространства более высокой размерности оказываются поддающимися осмыслению. См. Измерение.
• Мы можем проделать обратную процедуру! Координаты вводятся для того, чтобы позволить нам описать геометрические объекты с помощью наборов действительных чисел. В то же время в человеческом цветовосприятии мы обнаруживаем, что любой воспринимаемый цвет можно повторить и, что существенно, единственным образом, используя смесь трех базовых цветов, скажем, красного, зеленого и синего. Разные интенсивности красного, зеленого и синего обозначаются тремя положительными действительными числами, и каждая комбинация интенсивностей соответствует своему воспринимаемому цвету. Мы можем интерпретировать эти тройки как координаты трехмерного пространства свойств, а именно – пространства воспринимаемых цветов. Существует много примеров такого общего типа. Пространства, основанные на цветовых зарядах, играют центральную роль в нашей Главной теории.
• Мы можем определить, что мы имеем в виду под искривленными трех– (или более) мерными пространствами! Опять же, эти понятия сложно непосредственно представить. Но методы, которые мы используем для представления расстояний на картах, где мы изображаем поверхности на плоскости, могут быть выражены алгебраически, с использованием метрики, и после этого легко обобщены.
• Мы можем определить пространство-время, включая время в тот же базис, что и пространство! Чтобы это сделать, нам нужно всего лишь рассматривать дату события вместе с местом события как дополнительную координату. (Забавно заметить, что отрицательные числа незаметно появляются в датах до нашей эры. Можно, и пожалуй, нужно[105] было бы назвать пятый год до нашей эры минус пятым годом и писать ?5 г.) В общей теории относительности мы объединяем эту идею с предыдущей, чтобы дать определение искривленному пространству-времени.
• Мы можем использовать разные виды чисел! Координаты, основанные на комплексных числах, широко используются в квантовой теории, а координаты, основанные на грассмановых числах, позволили нам сформулировать многообещающую идею суперсимметрии.
Космические лучи
Cosmic rays
Когда мы говорим, что «видим» космос – звезды, туманности, галактики и т. д., – мы обычно имеем в виду, что мы принимаем часть электромагнитного излучения, которое эти объекты источают на Землю. (См. электромагнитный спектр.) На языке квантовой теории мы можем сказать, что мы видим их с помощью фотонов. Фотоны свободно распространяются через огромные пустые области пространства, и мы знаем, как управлять ими, используя линзы, чтобы получить изображения их источников. Под «пустыми» здесь я понимаю области, лишенные обычного вещества. Поскольку обычное вещество – по сути своей то, что возмущает движение фотонов, это определение отчасти закольцовано, – но смысл в том, что такие области существуют. Как мы обсудили в определении вакуума, пространство, которое является «пустым» в этом смысле, тем не менее содержит темную энергию, часто темную материю, одно или несколько полей Хиггса и беспрестанное бурление спонтанной квантовой активности (см. Квантовая флуктуация).
Космические объекты испускают, кроме фотонов, и другие частицы: электроны, позитроны, протоны и ряд более тяжелых атомных ядер, среди которых следует отметить ядра железа. Некоторые из этих частиц имеют огромную энергию – гораздо большую, чем энергия, достигнутая, например, на Большом адронном коллайдере, и некоторые из них добираются до Земли. Эти другие частицы, а также самые энергичные фотоны (гамма-излучение) мы называем космическими лучами. Те космические лучи, которые представляют собой электрически заряженные частицы, движутся по искривленным траекториям, поскольку они отклоняются галактическими магнитными полями. Это усложняет определение их источника.
В пионерские годы физики высоких энергий, до появления мощных ускорителей и коллайдеров, космические лучи были самым лучшим доступным источником частиц высоких энергий. В результате изучения космических лучей было сделано несколько фундаментальных открытий, включая существование позитронов, мюонов (m) и пионов (p). Возможно, что близкие контакты между частицами темной материи заставляют их аннигилировать в энергичные сгустки, которые могут быть источником необычных космических лучей. Сейчас проводится несколько экспериментов, исследующих такую возможность.
Коэффициент ветвления
Branching ratio
Когда частица может распадаться несколькими разными способами, мы говорим, что у нее есть несколько каналов распада, или ветвей распада. Относительная вероятность, с которой происходит какой-то конкретный распад, называется коэффициентом ветвления (или парциальной шириной распада). Так, если частица A распадается на B + C в 90 % случаев, а в D + E в 10 % случаев, то мы говорим, что коэффициент ветвления A в B + C равен 0,90, в то время как коэффициент ветвления в D + E равен 0,10.
Лептон
Lepton
Электрон e и его нейтрино ?e вместе с их родственниками мюоном µ и его нейтрино ?µ и ?-частицей и ее нейтрино ?? имеют общее название лептоны. Их античастицы являются антилептонами.)
Локальная симметрия
Local symmetry
Мы говорим, что симметрия локальна, когда она допускает, чтобы ее преобразования производились независимо друг от друга в различных точках пространства и в разные моменты времени.
Локальная симметрия вместе с квантовой теорией является основой Главных теорий всех четырех взаимодействий, которые объединяют наши современные познания об основных законах Природы. Вместе с суперсимметрией (и в рамках квантовой теории) она также является основой для одной заманчивой попытки унифицировать и улучшить Главную теорию, как описано в главе «Квантовая красота IV».
Локальная симметрия соотносится с общей (глобальной) симметрией, как анаморфное изображение со стандартной графической перспективой.
Локальная симметрия – один из важных фокусов нашего размышления, который преобладает в его последующих частях.
Магнетизм, магнитное поле, магнитный флюид
Magnetism/magnetic field/magnetic fluid
«Магнетизм» – это нестрогий термин для описания широкого круга явлений, связанных с силами воздействия электрических токов друг на друга и их взаимодействиями с немногими особыми магнитными веществами, которые обнаруживают подобные силы. Магнитные вещества, которые часто содержат железные руды, применяются, чтобы сделать всем известные магниты, используемые для стрелок компаса, магнитных держателей записок на холодильнике и для многого другого.
Техническое обсуждение точного определения магнитного поля и сил, которые оно вызывает, было бы в целом сходно с нашим обсуждением в статье про Электрическое поле, электрический флюид, но его детали значительно более сложны и расплывчаты. Я предлагаю два легко доступных издания, где вы можете найти больше информации на эту тему (см. в примечаниях в конце книги).
Масса
Mass
Научное понятие массы развивалось с течением времени, и это слово теперь используется в нескольких тесно связанных, но не полностью согласованных смыслах. Здесь я опишу три самых важных.
1. Самое раннее достаточно точное, научное использование понятия массы встречается в механике Ньютона. В ней масса воспринимается как основное свойство материи, которую невозможно создать, или уничтожить, или объяснить чем-то более простым. Масса – это мера инерции тела или его сопротивления ускорению. Тело с большой массой будет стремиться поддерживать постоянную скорость, если его не подвергнуть большим внешним воздействиям (силам). Такое понятие массы становится количественным во втором законе движения Ньютона, который гласит, что ускорение тела равно силе, действующей на него, разделенной на его массу. Понятие массы Ньютона все еще очень широко используется и все еще называется «массой», поскольку ньютоновская механика, хотя и не вполне точная, часто является достаточно хорошим приближением и ее легче использовать, чем более точную релятивистскую механику.
2. В эйнштейновской модификации механики, чтобы согласовать ее со специальной теорией относительности, масса стала другим понятием. В релятивистской механике масса – это свойство отдельных частиц, но масса может быть создана или уничтожена, когда частицы взаимодействуют друг с другом. В релятивистской механике масса является мерой вклада частицы в массовую энергию и определяет ее энергию движения. Масса – это свойство частиц, но это не четко определенное (сохраняющееся) свойство мира в целом.
У каждой из элементарных частиц нашей Главной теории есть определенная масса, но утверждение о том, что сумма масс частиц, вступающих во взаимодействие, равна сумме масс частиц после него, очень далеко от истины[106]. В столкновениях между электронами и позитронами высоких энергий обычно обнаруживается, что полная масса частиц после столкновения в сотни тысяч раз больше, чем полная масса частиц, участвовавших в нем изначально.
В релятивистской механике сохраняется не масса, но энергия. Мне нравится кратко подытоживать роль массы и энергии в релятивистской механике фразой: «У частиц есть масса, у мира есть энергия».
3. В космологии говорят о доле массы во Вселенной за счет различных составляющих: обычная материя (5 %), темная материя (27 %), темная энергия (68 %). Это – небрежное использование термина «масса». (У темной энергии, в частности, нет массы ни в одном из двух более привычных пониманий этого термина, определенных выше.) Но оно очень широко распространено как в научной, так и в популярной литературе, поэтому и нам от него никуда не деться. Это означает следующее: используя общую теорию относительности, мы можем связать скорость, с которой изменяется темп расширения Вселенной со временем – грубо говоря, его ускорение, – со средней плотностью энергии в ней. Мы можем разделить эту среднюю плотность энергии на квадрат скорости света, чтобы получить нечто измеренное в единицах плотности массы. Проценты, упомянутые выше, являются относительными вкладами в это «нечто», привнесенными различными видами материи.
Поскольку масса не сохраняется, по большом счету у нас есть надежда объяснить ее с точки зрения чего-то более простого. И действительно, есть чрезвычайно красивое объяснение источника большей части массы обычной материи, которое возникает из квантовой хромодинамики (КХД). Все важные элементы строения протонов – верхний и нижний кварки и цветные глюоны – имеют массу намного меньшую, чем масса протона, следовательно, у массы протона должен быть какой-то другой источник.
Ключевым шагом к пониманию происхождения массы протона будет как следует понять, что такое протон. Так что такое протон? С точки зрения современных представлений протон – это устойчивое, ограниченное в пространстве состояние возмущения в кварковом и глюонном флюидах. Такое состояние может перемещаться – галилеева симметрия уверяет нас в этом, – и, если мы смотрим на него издалека (по сравнению с его размером), оно будет похоже на частицу. Существует энергия поля глюонов, связанная с этим возмущением, и энергия движения кварков в состоянии конфайнмента. Если мы обозначим энергию стационарного возмущения за ?, то ?/c2 будет массой частицы, которой, как мы считаем, оно является, т. е. протона. И это – поразительным образом – источник вашей собственной массы. Это «масса без массы», возникающая из заключенной внутри энергии.
Массовая энергия
См. Энергия.
Мезон.
См. Адрон.
Метрика, метрический флюид
Metric/metric fluid
Мы говорим, что у пространства есть метрика, когда можно сказать, каково расстояние между двумя очень близкими точками. Сама метрика – это секретный соус, который превращает набор точек в структуру, имеющую размер и форму.
Давайте предположим для начала, что мы знаем, как измерить расстояние между двумя соседними точками в обычном пространстве, например, используя небольшие линейки. Тогда мы сможем измерить такими же линейками и расстояния между соседними точками на любой достаточно гладкой поверхности. Ограничение короткими линейками и близлежащими точками важно здесь потому, что, если мы имеем искривленную поверхность и длинные плоские линейки, тогда линейки могут плохо прилегать к поверхности на больших расстояниях, и мы не будем знать, как их правильно приложить.
Теперь давайте рассмотрим представление нашей поверхности с использованием обычной, плоской бумажной карты. Мы можем, конечно, сделать это разными способами, просто устанавливая соответствие между этими двумя множествами точек: точек на поверхности и точек на карте. Мы помещаем Прагу здесь, Нью-Дели там и т. д., заботясь о том, чтобы поместить по соседству на карте точки, которые находятся близко в действительности. Имеется немалая свобода в том, как это сделать, и в атласах можно найти много очень отличающихся представлений одной и той же области.
Без дальнейших указаний, однако, карта не говорит нам, насколько далеко представленные на ней точки в действительности разнесены на реальной поверхности. Метрика, дополнение к карте, и предоставляет эту информацию. Если быть немного точнее, метрика – это функция от положений на карте: она присваивает «вещь», или значение, каждой точке на карте. В каждой точке значение метрики – это инструмент, который дает вам для любого направления, в котором вы можете двигаться из этой точки, масштаб, который вы должны использовать на маленьких линейках, чтобы расстояние, которое вы измеряете между соседними точками на карте, было таким же, как расстояние между точками, которые они изображают на реальной поверхности.
Рассмотрев, что нужно сделать, чтобы превратить плоскую поверхность (нашу карту) в поверхность, обладающую размером и формой, мы можем творчески подойти к этой идее и развить ее или исполнить вариации на эту тему. Чтобы осознать концепцию метрики, наиболее важную для физики, мы должны сделать две вещи.
Во-первых, мы переключаем внимание с проблемы измерения поверхности, которая побудила нас ввести понятие метрики, к понятию метрики как таковому. Поэтому мы называем любой инструмент, показывающий нам масштабы, которые мы должны присвоить маленьким линейкам, метрикой на нашей карте, независимо от того, появился ли этот инструмент из самой поверхности или нет. (Делая этот шаг, мы следуем тем путем, которым Бернхард Риман [1826–1866] обобщил работу своего учителя Карла Гаусса [1777–1855].) Другими словами, мы даем такому понятию метрики собственную жизнь.
Во-вторых, мы добавляем некоторые измерения. Ничто не мешает нам добавить такой же тип определяющего масштаб механизма к точкам во всем трехмерном пространстве, а не только к точкам на плоском листе бумаги. Развивая эту мысль далее, мы можем использовать метод координат, чтобы представить трехмерное пространство и время как объединенное четырехмерное пространство-время, и рассмотреть добавление инструмента метрики к нему. Таким образом, мы нашли очень гибкую процедуру, которая может показывать – или, можно было бы сказать, определять, – что мы должны подразумевать под искривленным трехмерным пространством, или искривленным пространством-временем, делая это «наглядно правильным» образом, который обобщает то, как мы поступаем с поверхностями, где наша интуиция вполне ясна.
Скажем немного относительно математического понятия метрики. Это – абстрактный механизм, который заполняет пространство (или пространство-время), т. е. абстрактное поле. Среди других полей существуют: электрические поля, магнитные поля и поле скоростей в массе воды. В этих случаях и многих других мы обнаруживаем, что поля – важные элементы реальности. Они танцуют под музыку динамических уравнений, испытывают влияние материи и, в свою очередь, влияют на поведение материи. Мы можем сказать – не строго, но вполне справедливо, – что они физически существуют. Эйнштейн в его общей теории относительности постулировал, что метрика пространства-времени, так же как и эти другие поля, представляет собой физическую сущность, имеющую собственную жизнь. Мы называем ее метрическим флюидом или также гравитационным флюидом ввиду той роли, которую она играет в общей теории относительности.
Есть много вариантов и обобщений понятия «метрики», описанного в этой статье, которые полезны в различных приложениях. Общее между ними в том, что все они имеют дело с каким-либо расстоянием. Описанная выше версия в настоящий момент наиболее полезна в физике, и именно она фигурирует в нашей медитации.
Не во всех пространствах есть очевидное понятие расстояния, или же пространство может предлагать несколько различных возможностей, чтобы определить расстояние. В таких случаях мы можем или обойтись без метрики, или пробовать различные дополнительные возможности. Трехмерное пространство цветового восприятия является интересным примером в этом отношении.
Возможно ли определить точным количественным образом расстояние между различными воспринимаемыми цветами? Несколько серьезных мыслителей сражались с этой проблемой, включая, в частности, Эрвина Шрёдингера (известного благодаря уравнению Шрёдингера). Они придумали несколько разных ответов. Каждый из них внутренне непротиворечив, но пока еще ни один не оказался таким уж необычайно полезным или явно превосходящим остальные.
Механизм Хиггса
Higgs mechanism
Мы хотели бы использовать красивые уравнения локальной симметрии для описания слабого взаимодействия. Но эти уравнения, если применить их к пустому пространству, предполагают, что кванты флюида слабого взаимодействия – виконы – должны быть безмассовыми частицами, подобно фотонам. В действительности виконы имеют массы, превышающие массу протона в несколько десятков раз. Механизм Хиггса позволяет нам оставить красивые уравнения, при этом не впадая в противоречие с реальностью. Основная идея механизма Хиггса состоит в том, что пространство пронизано полем – полем Хиггса, которое видоизменяет поведение частиц по сравнению с тем поведением, которое бы они демонстрировали в случае его отсутствия.
Согласно механизму Хиггса, мы живем внутри сверхпроводника для токов слабого заряда.
См. Поле Хиггса, флюид Хиггса; Частица Хиггса, бозон Хиггса, а также подробное обсуждение в главе «Квантовая красота III», часть 3.
Микроволны, микроволновое фоновое излучение
Microwaves/microwave background radiation
Электромагнитные волны с длинами волн в диапазоне примерно от миллиметра до метра называют микроволновым излучением или просто микроволнами.
На ранней стадии своей истории материя в нашей Вселенной была настолько горячей и плотной, что атомы не могли существовать как целостные объекты. Плазма из протонов, ядер гелия и электронов была раскаленной добела, и Вселенная была заполнена светом. По мере того как Вселенная расширялась и охлаждалась, постепенно смогли сформироваться атомы, удерживающие свои электроны, и в результате – достаточно внезапно – Вселенная стала прозрачной для света и других форм электромагнитного излучения, каковой она остается и сегодня. Вездесущий свет продолжал наполнять Вселенную, но за счет продолжающегося расширения спектр света смещался к более длинным волнам.
К сегодняшнему дню большая часть того света оказалась смещенной в микроволновую часть электромагнитного спектра. Он превратился в микроволновое фоновое излучение[107].
Микроволновое фоновое излучение было обнаружено экспериментально Арно Пензиасом и Робертом Уилсоном в 1964 г., и с того момента оно является предметом интенсивных исследований. Благодаря его происхождению микроволновое фоновое излучение дает нам доступ к ничем не искаженной информации об условиях в очень ранней Вселенной.
Многогранник, или полиэдр
Polyhedron
Многогранник – трехмерное тело с плоскими многоугольными поверхностями, прямыми ребрами, где сходятся грани, и острыми вершинами, где сходятся ребра.
Многоугольник, правильный многоугольник
Polygon/regular polygon
Многоугольник – это фигура, полученная соединением последовательности точек на плоскости отрезками прямых линий, так, чтобы образовать замкнутый контур. Треугольники и прямоугольники – всем известные примеры многоугольников. Задающие точки многоугольника – те точки, где его стороны сходятся, – называются его вершинами.
Правильный многоугольник – это многоугольник, стороны которого имеют одинаковую длину и сходятся под равными углами во всех вершинах. Равносторонние треугольники – это правильные многоугольники с тремя сторонами, квадраты – правильные многоугольники с четырьмя сторонами и т. д.
Момент импульса
Angular momentum
Момент импульса наряду с энергией и импульсом (обычным импульсом, или количеством движения) является одной из выдающихся сохраняющихся величин классической физики. Каждая из них также развилась в основополагающий столп современной физики.
Момент импульса – наиболее сложная для определения и понимания из этих величин, и не стоит надеяться постичь всю его сложность без существенных усилий. Например, завораживающее, часто кажущееся нелогичным поведение волчков и гироскопов – следствие наличия у них момента импульса. Как следствие, наша медитация не слишком опирается на это понятие!
Момент импульса тела – это мера его углового движения (вращения) вокруг выбранного центра. Количественно он равен удвоенной скорости, с которой заметает площадь линия, нарисованная из центра тела, умноженной на массу тела. (Это нерелятивистская версия, верная для небольших скоростей. Специальная теория относительности приводит к похожей, но более сложной формуле.)
У момента импульса есть направление и величина. (Таким образом, это векторная величина – а именно это аксиальный вектор.) Чтобы определить направление, мы должны сначала определить моментальную ось вращения – т. е. направление, перпендикулярное к площади, заметаемой отрезком, – а затем выбрать положительное направление оси, используя правило правой руки. См. Четность.
Момент импульса системы тел равен сумме моментов импульса составляющих ее тел.
Существует широкий спектр обстоятельств, при которых момент импульса сохраняется. Этот результат лучше всего объясняется через общую теорему Нётер, которая связывает законы сохранения с симметрией. С этой точки зрения сохранение момента импульса вокруг некоторого центра вращения отражает симметрию (инвариантность) физических законов относительно преобразований, при которых происходит вращение пространства вокруг этого центра. Другими словами, момент импульса сохраняется, если законы не зависят ни от какого указанного внешним образом фиксированного направления.
Второй закон орбитального движения Кеплера, согласно которому отрезок, проведенный между планетой и Солнцем заметает одинаковую площадь за одинаковые отрезки времени, – это один из примеров сохранения момента импульса.
В квантовом мире момент понятие момента импульса не теряет своего смысла и приобретает новые черты утонченности и красоты. Именно математические свойства момента импульса в квантовой теории больше всего привлекли меня в физику, когда я был учеником и выбирал свой карьерный путь. Если вы хотите глубже изучить этот вопрос, вы можете обратиться к «Рекомендуемой литературе». Здесь я упомяну только то, что квантовые частицы зачастую проявляют непреодолимую вращательную активность, именуемую спином, похожим в каком-то смысле на нулевые колебания (см. Квантовая флуктуация) или на спонтанную активность квантовых полей.
Мультивселенная
См. Вселенная, видимая Вселенная и мультивселенная.
Мутатрон
Mutatron
В теориях, которые объединяют сильное и слабое взаимодействие, существуют частицы, которые вызывают преобразования между сильными и слабыми цветами. Мы (или, точнее, я) называем эти гипотетические частицы мутатронами[108].
Нанотрубка
Nanotube
Нанотрубки – это класс молекул, состоящих целиком из углерода. Как можно догадаться из названия, они имеют форму трубок и могут тянуться бесконечно в одном направлении. Нанотрубки могут иметь много разных размеров и форм, и они обладают замечательными механическими и электрическими свойствами. Например, некоторые классы нанотрубок чрезвычайно прочны в продольном направлении. Волокна, сделанные из таких нанотрубок, могут быть легкими, но более прочными, чем сталь. Более подробное обсуждение и иллюстрации см. в главе «Квантовая красота II».
Натуральные числа
Natural numbers
Числа 1, 2, 3, … – числа, которые естественным образом возникают в результате счета, – называют натуральными числами. Это тот вид чисел, которые Пифагор одобрял больше всего. Натуральные числа формируют дискретный ряд. Их следует отличать от действительных чисел.
Начальные условия
Initial conditions
Основные законы физики в рамках современного понимания являются динамическими уравнениями. Иными словами, они определяют, как состояние мира в один момент времени связано с его состоянием в другие моменты времени. Они, однако, не указывают нам, что мы должны принять в качестве начальной точки. Таким образом, мы должны задать начальные «условия», чтобы начать разворачивать наше описание.
Небесная механика
Celestial mechanics
Первоначально термин небесная механика означал приложение классической механики вместе с ньютоновской теорией гравитации к описанию движения больших тел – по большей части планет, их лун и комет – в Солнечной системе. Сегодня термин «небесная механика» используется более широко для обозначения приложения механики к астрофизическим телам, а также к ракетам и искусственным спутникам. Поскольку соответствующие законы физики применимы и в общем случае, небесная механика – это, в сущности, скорее специализированная ветвь механики, чем отдельная дисциплина.
Нейтрино
Neutrino
У каждого из трех электрически заряженных лептонов – электронов e, мюонов m и тау-частиц (тауонов) ? – есть связанное с ними нейтрино. Нейтрино, обозначаемые ?e, ?µ, ??, – электрически нейтральные частицы. Нейтрино с левой спиральностью несут единицу желтого слабого заряда, их электрический заряд равен нулю, а сильного цветового заряда они не имеют. Вследствие этого нейтрино участвуют в слабом взаимодействии, но не вступают в электромагнитные или сильные взаимодействия. В результате нейтрино чрезвычайно слабо взаимодействуют с обычным веществом. Яркая иллюстрация этого факта: каждую секунду приблизительно 65 миллиардов нейтрино, испускаемых при слабых переходах, которые питают энергией наше Солнце, проходят через каждый квадратный сантиметр на Земле. И тем не менее мы практически не чувствуем влияния этих нейтрино, и нужны очень сложные детекторы, чтобы вообще обнаружить этот поток.
Можно показать, что нейтрино должны были быть рождены в значительном изобилии при Большом взрыве. Получившийся космологический газ до сих пор не обнаружен, просто потому, что нейтрино так слабо взаимодействуют. Когда-то полагали, что нейтрино являются хорошим кандидатом на роль темной материи, но эта идея не выдержала критику – в основном потому, что теперь мы знаем, что они для этого слишком легкие.
Относительно нейтрино было обнаружено много других интересных фактов. Я предлагаю две легкодоступных публикации, где вы сможете найти больше информации по этой теме, в примечаниях в конце книги.
Нейтрон
Neutron
Нейтроны вместе с протонами являются строительными блоками атомных ядер. Нейтроны имеют нулевой электрический заряд, но весят примерно столько же, сколько протоны. Большая часть массы обычной материи возникает за счет массы составляющих ее протонов и нейтронов. Прежде полагали, что нейтроны являются базовыми элементарными частицами, но сегодня мы знаем, что они – сложные объекты, состоящие из более элементарных кварков и глюонов.
Непрерывная группа
См. Группа.
Непрерывная симметрия
Continuous symmetry
Если структура позволяет непрерывный ряд преобразований, который оставляет ее неизменной, или инвариантной – другими словами, если наша структура допускает гладкий ряд преобразований симметрии, мы говорим, что имеет место непрерывная симметрия структуры или что структура допускает непрерывную группу преобразований симметрии.
Пример: круг можно повернуть на любой угол вокруг его центра, и при этом он останется тем же самым кругом. Таким образом, круг инвариантен относительно гладкого ряда вращений. А вот равносторонний треугольник инвариантен только относительно поворотов вокруг центра на целое кратное угла 120°. Следовательно, равносторонний треугольник допускает дискретную, но не непрерывную симметрию.
См. также Аналоговый и Цифровой.
Непротиворечивость и противоречие
Consistency/contradiction
Мы говорим, что система, состоящая из предположений и наблюдений, непротиворечива, если ее нельзя использовать, чтобы вывести противоречие. Мы говорим, что мы имеем противоречие, если утверждение и его отрицание оказываются верны одновременно.
В чисто умозрительных теориях, которые не делают заявлений о конкретных физических явлениях, наблюдения не могут привести к противоречиям. Такая защищенность от противоречий делает эти теории непротиворечивыми, но хорошими они от этого не становятся. Ньютон убедительно выразил такое мнение в своих «Началах»:
Всё же, что не выводится из явлений, должно называться гипотезой; гипотезам же метафизическим, физическим, механическим или основанным на скрытых свойствах, не место в экспериментальной философии.
Оценивая ценность физических теорий, мы должны принимать во внимание не только их непротиворечивость, но также их силу и их экономность. Чтобы узнать больше на эту тему, см. Фальсифицируемая теория, сильная теория и Экономность (идей).
Нуклон
Nucleon
Нуклонами называются частицы, которые составляют атомные ядра. Нуклон означает просто «протон или нейтрон».
Нулевые колебания. См. Квантовые флуктуации и нулевые колебания.
Облако вероятности
Probability cloud
В классической механике частицы занимают в любой момент времени некоторое определенное положение в пространстве. В квантовой механике описание частицы совершенно иное. Частица не занимает определенное положение в любой момент времени; вместо этого ей ставится в соответствие облако вероятности, которое определено во всем пространстве. Форма облака вероятности может изменяться с течением времени, хотя в некоторых важных случаях оно не меняется. См. Стационарное состояние.
Название подсказывает, что мы можем представить себе облако вероятности как протяженный объект, который имеет некоторую неотрицательную, т. е. положительную или нулевую, плотность в каждой точке. Плотность облака вероятности в точке показывает, какова относительная вероятность того, что частица находится в этой точке. Таким образом, есть б?льшая вероятность найти частицу там, где плотность ее облака вероятности высокая, и меньшая вероятность найти ее там, где плотность этого облака низкая.
Квантовая механика не дает уравнений непосредственно для облаков вероятности. Облака вероятности вычисляются возведением в квадрат модулей волновых функций, удовлетворяющих уравнению Шредингера. См. Волновая функция, Уравнение Шредингера.
Общая ковариантность
General covariance
Это первоначальный термин Эйнштейна для локальной галилеевой симметрии[109], основного принципа общей теории относительности.
Общая теория относительности
General relativity
Общая теория относительности – это теория гравитации Эйнштейна.
Джон Уилер описал суть общей теории относительности таким образом:
Материя говорит пространству-времени, как ему искривляться.
Пространство-время говорит материи, как ей двигаться.
В основном тексте содержится подробное объяснение (и критика!) этого краткого резюме.
Слово «общая» в названии «общая теория относительности» – это выдумка Эйнштейна, призванная обозначить положение новой теории по отношению к его более ранней специальной теории относительности. В нашей медитации мы выражаем это отношение другим, более систематизированным языком, который развился в процессе описания других взаимодействий. Специальная теория относительности рассматривает преобразования Галилея, а общая теория относительности – более общие преобразования. Говоря в целом, они сводятся к тому, чтобы позволить использование различных преобразований Галилея в различных точках пространства-времени. На нашем языке общая теория относительности основана на локальной симметрии, тогда как специальная теория относительности – на нелокальной, или по-другому (и лучше), глобальной симметрии.
Объединение
Unification
Объединение связанных идей в согласованное целое – это аспект экономии мысли. Другой, дополнительный аспект объединения – снятие противоречий между кажущимися противоположностями. Примиряя противоположности, мы рассматриваем их в качестве взаимодополняющих аспектов лежащего в их основе единого целого.
Наш Вопрос ставит трудную задачу объединить красоту и физическое воплощение, или Идеальное и Реальное.
Объединение, как в его аспекте соединения связанных идей, так и в аспекте примирения кажущихся противоположностей, было главной чертой во многих знаковых достижениях физики:
• Систематическое использование координат, которое было впервые введено Рене Декартом (1596–1650) в его La G?om?trie 1637 г., объединившей алгебру и геометрию.
• Закон всемирного тяготения Ньютона и его законы движения объединили астрономию и земную физику. Наблюдения Галилея с помощью телескопа, которые открыли (среди прочего) гористый ландшафт нашей Луны и спутниковую систему Юпитера, стали мощными воплощениями этого объединения.
• Уравнения Максвелла для электромагнетизма объединили описание электричества и магнетизма. Эти же уравнения также дали нам описание света на основе электромагнетизма, собрав вместе все оптические явления в этом объединении.
• Специальная теория относительности Эйнштейна принесла с собой преобразования симметрии, которые смешивают пространство и время, позволяя нам видеть их как два аспекта объединенного пространства-времени.
• Электромагнитный флюид Фарадея и Максвелла и метрический флюид Эйнштейна, упраздняя Пустоту, объединили пространство-время и материю.
• Понятие квантов квантового флюида, типичными представителями которых являются фотоны электромагнитного излучения (света), объединило описание корпускулярных и волновых аспектов их физического поведения.
На переднем крае современной физики видны дразнящие указания на то, что скоро могут произойти новые объединения.
• Все разделы нашей Главной теории основаны на локальной симметрии, но преобразования, предусмотренные в наших теориях сильного, слабого и электромагнитного взаимодействий, совершаются независимо в пространствах свойств, в то время как преобразования, относящиеся к нашей теории гравитационного взаимодействия, совершаются в пространстве-времени. Мы ищем более всеобъемлющую локальную симметрию, которая сделает из них единое целое.
С помощью суперсимметрии мы могли бы объединить вещество и взаимодействие.
Именно эти идеи находятся в центре внимания в главе «Квантовая красота IV».
Обычная материя
Normal matter
«Обычная материя» – это удобный термин, который я использую, говоря о материи, состоящей из кварков, цветных глюонов, электронов и фотонов[110]. Обычная материя – доминирующая форма материи на Земле и в ее непосредственном окружении. Это тот вид материи, из которой сделаны мы сами и которую мы изучаем в химии, биологии, материаловедении, всех инженерных науках и почти всей астрофизике. Обычную материю следует отличать от темной энергии и темной материи.
Орбита, орбиталь
Orbit/orbital
Понятие орбиты планеты, вращающейся вокруг нашего Солнца, или орбиты искусственного спутника, вращающегося вокруг Земли, всем понятно и не требует здесь никакого специального комментария. Это, в сущности, последовательность положений, которые тело занимает в пространстве с течением времени, собранная в кривую.
Орбиталь, как она понимается в квантовой физике и химии, – это волновая функция стационарного состояния. Мы говорим, что электрон «занимает орбиталь», когда состояние этого электрона описывается волновой функцией, связанной с этой орбиталью. Термин «орбиталь» является пережитком модели атома Бора, в которой устойчивые состояния были связаны с определенными классическими орбитами.
Относительность, теория относительности
Relativity
В англоязычной физике слово «относительность» обычно является отсылкой к одной или сразу обеим теориям Эйнштейна, названия которых включают это слово, т. е. к Специальной или Общей теории относительности. Какая из двух подразумевается, должно быть ясно из контекста.
В нашей медитации мы подчеркиваем, что обе теории относительности по сути являются утверждениями о симметрии в нашем точно определенном смысле. Они утверждают, что мы можем совершить преобразования над величинами, которые фигурируют в законах физики, не изменив содержание этих законов – т. е. это Изменение без Изменения. Само слово «относительность» делает упор на аспект «изменения», но оставляет аспект «без изменения» – т. е. аспект инвариантности, важного дополнения к относительности – никак не озвученным. Эта случайность имела несчастье склонить некоторых людей к тому, чтобы предполагать и даже утверждать нелепости наподобие этой: «Эйнштейн учил нас, что все относительно». Он этому не учил, и это неверно.
Очарованный кварк
Charmed quark
Очарованный кварк, обозначаемый как c, – член второго семейства частиц материи. Очарованные кварки очень нестабильны, и их роль в нашем сегодняшнем мире очень невелика. Очарованные кварки были открыты в 1974 г., и их экспериментальное изучение весьма способствовало становлению Главной теории.
Перенормировка ренормализационная группа
Renormalization renormalization group
Квантовые флюиды лежат в самой основе нашей Главной теории. Они проявляют спонтанную активность, или способность к квантовым флуктуациям, которые в целом становятся все сильнее на коротких расстояниях. Эти непрерывные колебания пронизывают пространство и изменяют поведение, которое материя имела бы в их отсутствии. Расчет таких изменений называют перенормировкой.
Когда мы изучаем свойства частиц более пристально, двигаясь к более высоким энергиям или более коротким расстояниям или, как мы говорим, используя более высокое разрешение, мы меньше чувствуем влияние более плавных, слабых квантовых флуктуаций. Мы приближаемся к наблюдению «обнаженных» частиц. Ренормализационная группа – это математический аппарат для того, чтобы установить количественные связи между свойствами частицы, когда мы наблюдаем ее в различных разрешениях.
Асимптотическая свобода в сильном взаимодействии и количественное исследование объединения, которые обсуждаются в главе «Квантовая красота IV», являются хорошими примерами применения ренормализационной группы.
Период, периодический
Period/periodic
Периодический процесс – это такой процесс, который повторяется. Обычно термин относится к повторению во времени, хотя в научной литературе он нередко используется и для повторения в пространстве. Период процесса, периодического во времени, – это количество времени, которое проходит между повторениями. См. также Частота.
Период колебания
См. Частота.
Периодическая таблица
Periodic table
Периодическая таблица химических элементов[111] – это содержательное и информативное геометрическое расположение списка химических элементов, в котором столбцы содержат элементы со сходными химическими свойствами. В каждом столбце атомные номера и атомные веса увеличиваются в направлении сверху вниз; в каждой строке атомные номера и атомные веса увеличиваются, когда мы движемся слева направо. В самой развернутой версии периодической таблицы атомный номер увеличивается на единицу при переходе в соседнюю справа клетку, а также когда мы переходим из самой правой клетки ряда в крайнюю левую клетку рядом ниже. (Есть много вариантов представления таблицы. Зачастую, например, выделяют редкоземельные элементы и актиноиды в отдельные подтаблицы.)
Квантовая механика объясняет структуру периодической таблицы теоретически, как следствие уравнения Шрёдингера. Это великолепный пример соответствия
Идеальное ? Реальное.
В этом объяснении основную роль играют квантовая теория момента импульса и принцип запрета Паули.
Перспектива
См. Проективная геометрия и перспектива.
Платоново тело, платонова поверхность
Platonic solid/Platonic surface
Платоново тело (правильный многогранник) – это многогранник, все грани которого являются копиями одного и того же правильного многоугольника и чьи грани соединяются единообразно во всех вершинах. Есть ровно пять различных (конечных) платоновых тел: тетраэдр, октаэдр, икосаэдр, куб и додекаэдр. Они подробно описаны в основном тексте.
Математическое построение этих тел и доказательство того, что иные невозможны, являются кульминационным моментом «Начал» Евклида.
Поверхности правильных многогранников во многих отношениях более фундаментальны, чем сами тела, которые они ограничивают. Я называю их платоновыми поверхностями.
Платоновы тела внушали восхищение математикам, ученым и мистикам в течение многих столетий.
Поглощение (Абсорбция)
Absorption
Мы говорим, что частица поглотилась, если закончилось ее независимое существование. Поскольку полная энергия сохраняется, энергия частицы после этого переходит в другую форму. Например, когда частица света (фотон) достигает вашей сетчатки, она может быть поглощена белками (родопсинами), которые в результате поглощения меняют форму. Изменение их формы, в свою очередь, вызывает электрические сигналы, которые наш мозг интерпретирует как зрительное ощущение.
Позитрон
Positron
«Позитрон» – это другое название для антиэлектрона, античастицы электрона.
Поле и флюид
Field/fluid
Введение понятие поля, пожалуй, лучше начать с примеров.
• При описании погоды удобно учитывать значения температур во многих точках пространства в различные моменты времени. Совокупность этих значений определяет температурное поле.
• При описании движения в толще воды удобно рассматривать значение скорости воды во многих точках пространства в различные моменты времени. Совокупность этих значений определяет поле скоростей.
• При описании электрических явлений удобно рассматривать, какие силы действовали бы на электрически заряженную частицу в случае ее наличия в различных точках пространства в различные моменты времени. Деление величин этих сил на величину заряда приведет нас к определению электрического поля.
В целом мы говорим, что у нас есть «поле типа X», когда у нас есть значения X в различных точках пространства и времени. Иначе говоря, поле типа X дает нам величину типа X в виде пространственно-временной функции.
Термин «флюид», используемый в этой книге, относится к любой разновидности того, что заполняет пространство и проявляет активность. Примеры включают электрический флюид, магнитный флюид, глюонный флюид и флюид Хиггса. Для того чтобы узнать о более тонких, но важных различиях между полем и флюидом, см. главным образом Электрическое поле и электрический флюид.
См. также Среда.
Поле Хиггса, флюид Хиггса
Higgs field/Higgs fluid
Флюид Хиггса – это заполняющая пространство субстанция, которая участвует в уравнениях Главной теории. Поле Хиггса – это мера усредненного воздействия флюида Хиггса на другие частицы. См. Поле, флюид; Электрическое поле, электрический флюид, а также подробное обсуждение в главе «Квантовая красота III», часть 3.
Поперечная волна и поляризация (света)
Transverse wave/polarization of light
В нашей медитации самые важные поперечные волны – это электромагнитные волны, включая свет как особый случай.
Когда электромагнитная волна распространяется через пространство, лишенное обычного вещества (см. Вакуум), ее электрическое и магнитное поля – оба из которых являются направленными, векторными величинами – перпендикулярны направлению распространения волны. Именно это, не больше и не меньше, мы имеем в виду, говоря, что электромагнитные волны являются поперечными волнами. Таким образом, для поперечной волны активность, которую производит волна, перпендикулярна направлению, в котором волна распространяется.
В отличие от электромагнитных звуковые волны не являются поперечными волнами. Их активность, сжатие и разрежение воздуха, вызывает движение частиц воздуха в том же самом направлении, что и направление распространения волны. Волны такого типа называют продольными волнами.
Даже самые простые виды световых волн, связанные с чистыми спектральными цветами, имеют дополнительное свойство помимо их цвета и направления распространения. Это свойство называют поляризацией. Самая простая возможная поляризация – линейная поляризация. Если световая волна идет прямо на вас и ее электрические поля всегда указывают в направлении, которое соединяет вашу голову и ноги, когда вы стоите, мы говорим, что свет линейно поляризован в вертикальном направлении. Существуют решения уравнений Максвелла, которые соответствуют линейной поляризации в любом поперечном направлении, т. е. в любом направлении, перпендикулярном к направлению распространения волны. Есть также другие, более сложные возможные поляризации, когда за период колебаний электрические поля описывают круги или эллипсы в плоскости, перпендикулярной направлению распространения волны. В таких случаях мы получаем свет с круговой или эллиптической поляризацией.
Люди нечувствительны к поляризации света (с некоторыми незначительными исключениями), хотя многие другие животные, особенно насекомые и птицы, ощущают ее.
Постоянная Планка, приведенная постоянная Планка
Planck constant/reduced Planck constant
В 1900 г. Макс Планк (1858–1947), изучая, как электромагнитный флюид приходит в равновесие с горячими газами, нашел необходимым предположить, что передача энергии между материей и электромагнитным излучением происходит не сколь угодно малыми порциями, а исключительно квантованными единицами. Он счел необходимым постулировать, что минимальная единица передачи энергии пропорциональна частоте света. Коэффициент пропорциональности, возникающий в этом соотношении – соотношении Планка – Эйнштейна, – теперь известен как постоянная Планка.
Эйнштейн предположил затем, что соотношение Планка – Эйнштейна применимо к электромагнитному флюиду как таковому, а не только к его обмену энергией с атомами. Бор в своей модели атома предложил правила для определения стационарных состояний электрона в атоме водорода, в которых постоянная Планка играла центральную роль. Успех правил Бора в объяснении спектра водорода ввел постоянную Планка в теоретическое описание вещества, так же как и в описание света.
В современной квантовой теории постоянная Планка стала вездесущей. Важный пример – ее появление в описании спина частиц. Многие виды частиц, включая электроны, протоны, нейтрино и нейтроны, имеют «спин ?». Как описано в статье о Спине, это означает, что они проявляют самопроизвольное вращательное движение. Постоянная Планка появляется в количественном описании этого движения. Указанное вращательное движение, в частности, обладает величиной момента импульса, равной одной второй приведенной постоянной Планка (которая является просто постоянной Планка, поделенной на 2?).
Потенциальная энергия
См. Энергия.
Поток
Flux
Векторные поля независимо от их природы можно математически рассматривать как представление потока обычной текучей среды, такой как воздух или вода. Математически воображаемый поток в каждой точке пространства имеет скорость, пропорциональную значению фактического векторного поля в этой точке. В этой модели поток через поверхность – это просто показатель скорости, с которой жидкость проходит через эту поверхность (с точностью до знака, что мы сейчас и обсудим). Это определение потока имеет смысл независимо от того, есть ли у этой поверхности граница.
Таким образом, если мы рассмотрим текущую реку и представим поверхность, расположенную перпендикулярно течению, то поток через эту поверхность будет существенным. В то же время поток будет несущественным через поверхности, повернутые по большей части вдоль потока.
Теперь вам нужно обратиться к статье Циркуляция – потому что, вероятно, вы еще этого не сделали! Дело в том, что я сейчас заполню пробел, касающийся одной последней тонкости о взаимосвязи этих двух понятий. После этого вы будете знать все, чтобы действительно понять, что такое уравнения Максвелла, используя только геометрические понятия и образы.
В двух уравнениях Максвелла нам нужно рассматривать поверхность, ограниченную замкнутым контуром и сравнивать циркуляцию чего-то одного по этому контуру с потоком чего-то другого через эту поверхность. (В законе Фарадея мы связываем циркуляцию электрического поля с потоком магнитного поля; а в законе Ампера – Максвелла мы связываем циркуляцию магнитного поля с потоками электрического тока и электрического поля.)
Чтобы подсчитать циркуляцию для использования в этих уравнениях, мы должны определиться с направлением, в котором мы движемся по контуру. Есть две возможности – и ответы, которые они дают для циркуляции, различаются знаком. Чтобы уравнения Максвелла оставались одинаковыми независимо от нашего выбора, мы должны гарантировать, что знак потока через поверхность также меняется, когда мы меняем направление обхода контура, ограничивающего эту поверхность (и таким образом – знак циркуляции).
С этой целью мы используем простое правило правой руки: если пальцы вашей правой руки следуют направлению контура, то в определении потока мы считаем перенос жидкости положительным, когда он происходит в направлении вашего большого пальца, и отрицательным в случае обратного направления[112]. Если мы следуем этому правилу, то изменение направления обхода контура изменит одновременно и знак циркуляции, и знак потока, и таким образом взаимосвязь между циркуляцией и потоком останется неизменной.
В двух других уравнениях Максвелла (описывающих электрический и магнитный законы Гаусса) мы рассматриваем поток через замкнутую поверхность. В таком случае мы считаем поток положительным, если он переносит жидкость изнутри поверхности вне ее, и отрицательным в противном случае.
Преобразования Галилея, галилеева симметрия, галилеева инвариантность
Galilean transformation/Galilean symmetry/Galilean invariance
Преобразования Галилея – это вид преобразований, который мы совершаем над системой, когда мысленно прибавляем или вычитаем некоторую постоянную скорость из движения всех ее частей. Галилей, как это описано в основном тексте, описывал красивый мысленный эксперимент, который убедительно показывает, что после преобразований Галилея физические законы остаются неизменными, т. е. инвариантными: если вы находитесь в закрытой каюте без окон на корабле при спокойной погоде, то из того, что вы наблюдаете и ощущаете внутри каюты, невозможно сказать, как быстро движется корабль. Гипотеза о том, что законы физики инвариантны относительно преобразований Галилея, или, по-другому, о том, что законы физики обладают галилеевой симметрией, является одним из столпов специальной теории относительности. См. также Буст.
Принцип запрета Паули или просто принцип запрета
Pauli exclusion principle/exclusion principle
Принцип запрета Паули в его первоначальной форме утверждает, что два электрона не могут находиться в одном и том же квантовом состоянии. Этот принцип применим ко всем фермионам: никакие два тождественных фермиона не могут находиться в одном и том же квантовом состоянии. Нежелание электронов и фермионов в целом делать одно и то же приводит к эффективному отталкиванию между ними. Это отталкивание является чисто квантово-механическим эффектом, который дополняет более привычные силы, такие как электрические силы.
Принцип запрета является существенным для понимания атомов, поскольку он не дает электронам в атоме сгрудиться около его ядра, несмотря на мощное электрическое притяжение последнего. Внешние электроны, удаленные от ядра, открыты влиянию соседних атомов. Таким образом принцип запрета делает возможной химию.
Проективная геометрия и перспектива
Projective geometry/perspective
Проективная геометрия – это обширная область математики, тесно связанная с художественным изучением перспективы. Ее основная задача – понять связи между изображениями, которые мы получаем, когда смотрим на один и тот же объект с различных точек наблюдения (иначе говоря, под различными ракурсами). Что общего имеют эти изображения? Как можно воспользоваться информацией из одного такого изображения, чтобы построить другие? Вот примеры вопросов, которые решаются в проективной геометрии. Проективная геометрия демонстрирует нам интересное применение глубоких идей, включая преобразование, симметрию, инвариантность, относительность и дополнительность, как объясняется в основном тексте.
Проекция
Projection
Это слово используется в математике и физике очень гибко. Оно имеет не одно, а несколько различных точных технических определений в пределах различных областей знаний. Во всех случаях проекция – это отображение одного пространства на другое, с помощью которого информация о первом пространстве представляется в новой форме. Часто (но не всегда) часть информации в этом процессе теряется. В этой книге я использовал слово «проекция» достаточно неформально, без технической скрупулезности, в нескольких тесно связанных смыслах:
• Проекция теней в метафоре Пещеры Платона. Здесь тени создают двумерные бесцветные версии объектов, которые они представляют, и много информации теряется.
• Проекция, которую создают наши глаза, наше зрение. Сетчатка наших глаз получает двумерный образ трехмерного мира. Фокусировка хрусталиком глаза позволяет создавать изображения, в которых (в случае идеального зрения) весь свет, выходящий из некоторой точки рассматриваемого объекта, фокусируется в очень небольшую область на сетчатке, сохраняя таким образом важную пространственную информацию.
Как мы подробно обсуждали в главе «Максвелл II», входной электромагнитный сигнал, который мы называем светом, несет в себе гораздо больше информации, чем извлекают наши глаза.
Человеческое зрение выполняет проекцию бесконечномерного пространства интенсивностей спектральных цветов на трехмерное пространство воспринимаемого цвета и отбрасывает информацию о поляризации.
• Геометрическая проекция: проекция поверхностей правильных многогранников на описанные вокруг них сферы путем продолжения линий из центра до поверхности; проекция световых лучей на холст в геометрически точном рисовании (вдохновленная живописью наука о перспективе); проекция поверхностей, таких как участки местности или даже вся поверхность Земли, на плоские листы бумаги при создании географических карт.
• Цветовая проекция в пространстве цветовых свойств. Например, на цветной вклейке X мы спроецировали трехмерное пространство цветовых свойств, координатами которого являются интенсивности R, G, B – красного, зеленого и синего цвета соответственно – на двумерное пространство свойств, просто отбросив одну из координат.
Пространство свойств
Property space
Изучая человеческое восприятие цветов, мы обнаруживаем, что любой воспринимаемый цвет может быть представлен по существу единственным образом – путем смешения трех основных цветов, например, красного, зеленого и синего. Различные интенсивности красного, зеленого и синего описываются тремя положительными действительными числами, и каждая такая комбинация интенсивностей соответствует своему особому воспринимаемому цвету. Мы можем интерпретировать эти тройки как координаты в трехмерном пространстве свойств – пространстве воспринимаемых цветов.
Есть много примеров подобного рода, где мы используем числа для обозначения свойств и рассматриваем наборы чисел как координаты, чтобы определить пространство свойств. Пространства свойств, основанные на цветовых зарядах, играют центральную роль в наших Главных теориях.
Протон
Proton
Протоны наряду с нейтронами являются строительными блоками атомных ядер. Протоны имеют противоположный по отношению к электронам электрический заряд и весят примерно в две тысячи раз больше. Большая часть массы обычного вещества появляется за счет массы протонов и нейтронов, входящих в нее. Раньше думали, что протоны являются элементарными частицами, но сегодня мы знаем, что это сложные объекты, построенные из более элементарных кварков и глюонов.
Редукционизм
Reductionism
Уничижительный термин для «Анализа и Синтеза». См. Анализ и Синтез.
Сверхпроводимость, сверхпроводник
Superconductivity/superconductor
Многие металлы и некоторые другие материалы проявляют качественно иное поведение, когда они охлаждены до температуры, близкой к абсолютному нулю. Наиболее существенно то, что их сопротивление протеканию электрического заряда резко падает до нуля. Говорят, что они проявляют сверхпроводимость и становятся сверхпроводниками.
Сверхпроводимость была обнаружена экспериментально Камерлинг-Оннесом в 1911 г. Много лет ее не удавалось объяснить теоретически. Прорыв случился в 1957 г., когда Джон Бардин, Леон Купер и Роберт Шриффер предложили то, что мы теперь называем теорией сверхпроводимости БКШ. Их работа не только объяснила появление сверхпроводимости, но сделала это с использованием очень красивых и мощных идей, которые могли быть – и были – применены к другим задачам. В частности, они предвосхитили спонтанное нарушение симметрии и механизм Хиггса.
В сверхпроводниках фотоны ведут себя так, будто у них есть ненулевая масса. Уравнения, которые описывают эту ситуацию, по сути такие же, как и уравнения, которые мы используем в Главной теории, чтобы придать ненулевую массу виконам в механизме Хиггса. Я думаю, что будет справедливо и поэтично сказать, что большой урок, который мы можем извлечь из открытия частицы Хиггса, состоит в том, что мы живем внутри космического сверхпроводника. (Но это сверхпроводимость для потока слабого заряда, а не электрического заряда.)
Семейство, поколение
Family
Частицы вещества в Главной теории – т. е. кварки и лептоны – имеют одну интересную особенность – трехкратное повторение. Говорят, что они образуют три семейства (по-русски их также называют поколениями). В каждом семействе насчитывается 16 частиц, образующих схожие структуры из сильных, слабых и электромагнитных зарядов, которые подробно описываются в основном тексте. Представители трех семейств перечислены в нижеследующей таблице.
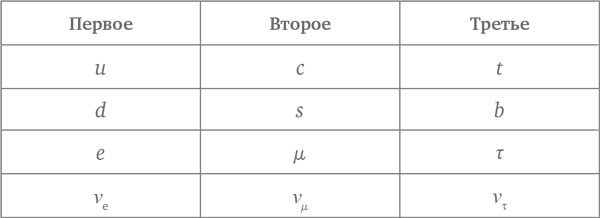
По-другому, пользуясь геометрическим языком главы «Квантовая красота III», мы можем сказать, что каждое из трех семейств содержит шесть сущностей, занимающих в каждом случае одни и те же пространства свойств.
Переходы, связанные со слабым взаимодействием, которые превращают единицу желтого слабого заряда в единицу фиолетового слабого заряда, превращают (левый) u-кварк в (левый) d-кварк, как мы обсудили в основном тексте. Там я ссылался на некоторые сложности и здесь расскажу об этом подробнее. Сложность состоит в том, что переходы слабого цвета могут сопровождаться переходами между семействами. Таким образом, кроме u ? d, мы имеем также u ? s и u ? b. Чтобы описать относительные вероятности таких переходов, необходимо ввести в Главную теорию новые параметры. Угол Кабиббо, например, является мерой того, как соотносятся вероятности второго и первого. Существует множество дополнительных переходов между кварками, которые нужно учесть (например, c ? d), и еще больше, если вспомнить о лептонах. Чтобы описать их все в рамках Главной теории, необходимо ввести около дюжины новых параметров. Величины этих «углов смешивания» были измерены экспериментально, но нет никакой убедительной теории, объясняющей, почему они именно такие.
Ну и уж коли на то пошло, нет убедительной теории, которая бы объясняла, почему вообще Природа позволила себе это трехкратное повторение семейств.
Сила, взаимодействие
Force
В физике и в нашей медитации термин сила может употребляться двумя различными способами.
В ньютоновской механике сила – это мера влияния одного тела на другое. Сила, с которой действует тело, – это его способность вызывать ускорение других тел. См. Ускорение.
В другом варианте употребления (который часто встречается, но менее точен) мы говорим о силах Природы, имея в виду те механизмы, которые действуют в Природе. В нашей Главной теории мы выделяем в Природе четыре фундаментальные силы: гравитация, электромагнетизм, а также сильная и слабая сила. Также в этом случае часто говорят о взаимодействиях вместо сил (и следовательно, об электромагнитном взаимодействии, сильном взаимодействии и т. д.). Я решил повсюду использовать слово «сила», поскольку это звучит сильнее[113].
Силовые линии
Lines of force
Под влиянием стержневого магнита железные опилки на листе бумаги образуют кривые линии, идущие от одного полюса магнита к другому, как изображено на илл. 35. Это красивое явление и другие подобные вдохновили воображение Фарадея. Он пришел к предположению, что эти линии существуют сами по себе, заранее, и железные опилки их лишь проявляют, а не создают. Эти интуитивные догадки привели его к новым экспериментальным открытиям. Максвелл развил эти результаты в точно сформулированные математические идеи. Современная физика с ее флюидами, заполняющими пространство, появилась из этих идей. Они вытеснили идею дальнодействия как модель фундаментального понимания устройства мира.
Сильное взаимодействие
Strong force
Сильное взаимодействие наряду с гравитацией, электромагнетизмом и слабым взаимодействием – это один из четырех основных механизмов, через которые действует Природа.
Сильное взаимодействие – самая мощная сила в Природе. Оно отвечает за стабильность атомных ядер и управляет большей частью того, что происходит при столкновениях, которые изучаются на ускорителях высоких энергий, таких как Большой адронный коллайдер.
Вскоре после открытия атомных ядер в начале XX в. физики признали, что взаимодействия, известные к тому времени – гравитация и электромагнетизм, – не могли объяснить самые основные свойства ядер, начиная с их способности сохранять стабильность. Это привело к десятилетиям интенсивных исследований в ядерной физике высоких энергий, как экспериментальных, так и теоретических. Зрелый результат этой работы – Главная теория, подробно описанная в нашей основной медитации. В рамках Главной теории сильное взаимодействие понимают как проявление квантовой хромодинамики (КХД).
В английском языке вместо термина «сильное взаимодействие» (strong interaction) чаще используется выражение strong force (буквально «сильная сила»). Лишь в некоторых случаях, таких как обсуждение гравитационного влияния нейтронной звезды или черной дыры, приходится говорить о большой величине силы в буквальном смысле. Поскольку в русском языке выражение «сильная сила» практически не применяется, неоднозначности не возникает. См. Сила, взаимодействие.
Симметрия, преобразования симметрии, группа симметрии
Symmetry/symmetry transformation/symmetry group
В математике и математических науках мы говорим, что у объекта есть симметрия, если существуют преобразования, которые производят изменения или перемещают различные части объекта, оставляя объект в целом неизменным, или инвариантным. Такие преобразования называют преобразованиями симметрии.
Понятия симметрии и преобразований симметрии также применяются к системам уравнений. Мы говорим, что система уравнений имеет симметрию относительно некоторого преобразования, если преобразование изменяет величины, которые стоят в уравнениях (как правило, меняя их местами, или комбинируя их более сложными способами) без изменения смысла системы уравнений в целом.
Пример: уравнение x = y обладает симметрией относительно преобразования, которое меняет местами x и y, потому что преобразованное уравнение y = x имеет тот же самый смысл, что и исходное. Все множество преобразований, которые оставляют объект инвариантным, называют его группой симметрии.
Синтез
Synthesis
Процесс объединения простых компонентов или понятий для того, чтобы произвести более сложные структуры. См. Анализ и Синтез.
Скорость
Velocity
Интуитивно скорость определяется как быстрота изменения положения.
Таким образом, чтобы определить скорость частицы, мы рассматриваем ее смещение ?x за малый интервал времени ?t, берем частное от деления ?x/?t и рассматриваем его предельное значение при уменьшении и стремлении интервала ?t к нулю. Это предельное значение, по определению, является скоростью.
См. Бесконечно малые, где обсуждаются некоторые фундаментальные вопросы, касающиеся этого определения.
Слабое взаимодействие
Weak force
Слабое взаимодействие наряду с гравитацией, электромагнетизмом и сильным взаимодействием – это один из четырех основных механизмов, с помощью которых действует Природа.
Слабое взаимодействие ответственно за большое разнообразие процессов трансформации, включая некоторые формы ядерной радиоактивности, «горение» ядерного топлива внутри звезд и космологический и астрофизический синтез всех химических элементов (их ядер), начиная с протонов и нейтронов.
В рамках Главной теории слабое взаимодействие понимают как результат реакции частиц W и Z, так называемых виконов, на слабый цветовой заряд. Как и другие фундаментальные взаимодействия, слабое взаимодействие – проявление локальной симметрии.
Для объяснения особенностей слабого взаимодействия, в частности, ненулевой массы виконов, был предложен механизм Хиггса. Развитие этого подхода привело к открытию частицы Хиггса. Успех этих идей говорит нам о существовании поля Хиггса, которое пронизывает все пространство и изменяет поведение других частиц разнообразными способами.
В английском языке вместо термина «слабое взаимодействие» (weak interaction) чаще используется выражение weak force (буквально «слабая сила»). В буквальном смысле оно уместно, например, если вы приводите доводы против астрологии и говорите о влиянии на человеческие судьбы силы тяжести планеты или далекой звезды: «Это такая слабая сила, что она не может иметь никакого значения». Поскольку в русском языке выражение «слабая сила» практически не применяется, неоднозначности не возникает. См. Сила, взаимодействие.
Слагаемое Максвелла (Закон Максвелла)
Maxwell term (Maxwell's law)
Чтобы согласовать расхождения между динамическими законами для электрического и для магнитного поля в том виде, в каком они были тогда известны, Максвелл предположил, что должен существовать дополнительный эффект. Новый эффект, который я назвал законом Максвелла, состоит в том, что меняющиеся со временем электрические поля вызывают («создают») магнитные поля. Это своего рода комплементарное дополнение к закону Фарадея, который утверждает, что меняющиеся со временем магнитные поля вызывают появление электрических полей. Закон Максвелла добавил другой способ наведения магнитных полей к уже известному – с помощью электрических токов (Закон Ампера). Полное уравнение, которое получается при добавлении нового слагаемого Максвелла к закону Ампера, известно как закон Ампера – Максвелла.
Собственная частота, резонансная частота
Natural frequency/Resonant frequency
Многие объекты, особенно жесткие, обладают несколькими предпочтительными типами колебаний. Их называют собственными модами колебаний. В каждой собственной моде объект проходит сквозь цикл изменений формы, который повторяется через фиксированный интервал времени. Этот интервал называют периодом моды колебаний, а величину, обратную этому периоду, – частотой моды. Частоты этих естественных режимов колебаний называют собственными частотами. Поскольку колебания тел в воздухе вызывают звуковые волны, мы можем слышать собственные частоты тел как чистые тона, которые они издают.
Примеры:
• Камертоны делаются так, чтобы иметь единственную слышимую собственную частоту.
• У гонгов обычно есть несколько собственных частот, так же как и у колоколов. Можно слышать различные комбинации тонов при колебаниях гонга или колокола, в зависимости от того, где или как по ним ударили. Это происходит потому, что разные типы ударов устанавливают различные начальные условия, возбуждают разные собственные моды с различной относительной силой.
Собственные частоты тела также называют его резонансными частотами.
Эти явления в музыкальных инструментах и звуке имеют близкие параллели в атомах и световых явлениях. Собственные моды инструмента напоминают стационарные состояния атома, а звуковая палитра музыкального инструмента походит на спектр атома. Эти параллели не только метафоричны, но простираются и до уравнений, описывающих эти системы, которые очень похожи друг на друга. В спектрах атомов проявляется очень реальная, видимая Музыка сфер.
Спектральный цвет
См. Цвет (света) и электромагнитный спектр.
Спектры атомные, молекулярные и прочие
Spectra atomic, molecular, and other
Атомы определенного вида – например, атомы водорода – поглощают некоторые спектрально чистые цвета гораздо эффективнее, чем другие. (Вообще говоря, они поглощают электромагнитные волны некоторых частот гораздо сильнее, чем волны с другими частотами. В этой словарной статье я буду использовать менее общий, но более наглядный язык цветов.) Те же самые атомы при нагреве испускают большую часть излучения в виде тех же самых спектрально чистых цветов. Комбинация характерных цветов различна для разных видов атомов и образует своего рода отпечатки пальцев, благодаря которым мы можем их идентифицировать. Комбинация тех цветов, которые предпочитает атом, называется его спектром.
Большим достижением квантовой теории было обнаружение способа вычисления атомных спектров. Идея, лежащая в его основе, до сих пор является актуальным наследием модели атома Бора. Бор постулировал, что электроны в атоме могут находиться только в дискретном наборе стационарных состояний. Поэтому возможные значения энергии электронов также образуют дискретный набор. Когда атом испускает или поглощает фотон, он совершает переход между двумя стационарными состояниями. Поскольку в этом процессе сохраняется энергия, энергия фотона соответствует разнице энергий этих двух стационарных состояний. Наконец, венец проницательности Бора: спектральный цвет фотона соответствует его энергии. Таким образом, в спектре атома закодированы энергии его возможных состояний. (Скажем точнее об этом коде: частота электромагнитной волны соответствующего цвета, помноженная на постоянную Планка, равна энергии фотона. См. Фотон и соотношение Планка – Эйнштейна.)
В современной квантовой теории мы вычисляем возможные стационарные состояния и их энергии, решая уравнение Шрёдингера, но фундаментальное соотношение между возможными энергиями атома и его спектром остается таким же, каким его представлял Бор. См. Уравнение Шрёдингера.
Я говорил об атомах, но та же самая логика применима к молекулам, к твердым телам, к ядрам и даже к адронам. В ядрах мы имеем дело со стационарными состояниями нуклонов, а в адронах – со стационарными состояниями систем, состоящих из кварков и глюонов, но в каждом случае в их спектрах закодированы секреты их структуры.
Когда свет Солнца или других звезд анализируют и изучают его спектральный состав, обнаруживается, что некоторые цвета имеют большую интенсивность (так называемые «эмиссионные линии»), а другие – меньшую интенсивность (так называемые «линии поглощения») по сравнению со средним уровнем. Картина эмиссионных линий и линий поглощения может быть сопоставлена со спектрами (измеренными либо вычисленными) известных атомов, молекул и ядер. Они показывают, что находится в атмосфере звезды и есть ли там горячие или холодные зоны. Они предоставляют очень подробные и убедительные свидетельства того, что вещество повсюду во Вселенной состоит из одного и того же материала и подчиняется тем же самым законам.
Употребление слова «спектр» в словосочетании «электромагнитный спектр» кажется на первый взгляд сильно отличающимся от его использования в словосочетании «спектр атома». Первое относится ко всему диапазону возможных форм электромагнитного излучения, в то время как последнее относится к определенным цветам (или к чистым тонам, т. е. частотам) света, которые атом может испускать (который однозначно соответствует, как мы объяснили выше, возможным энергиям его стационарных состояний). Однако если смотреть глубже, то станет ясно, что вполне справедливо можно сказать, что электромагнитный спектр – действительно спектр чего-то, а именно: электромагнитного флюида! Ведь электромагнитный спектр – это диапазон возможных цветов, которые может испустить электромагнитный флюид.
Специальная теория относительности
Special relativity
В своей специальной теории относительности Эйнштейн соединил две идеи, которые кажутся противоречивыми.
• Наблюдение Галилея о том, что совокупное движение системы с постоянной скоростью оставляет законы Природы неизменными.
• Вывод из уравнений Максвелла о том, что величина скорости света – следствие законов Природы и не может меняться.
Между этими двумя идеями очевидно внутреннее противоречие, поскольку опыт с прочими объектами подсказывает, что наблюдаемая нами скорость этих объектов изменится, если мы сами будем перемещаться с постоянной скоростью. Мы можем их догнать или даже опередить. Почему лучи света должны вести себя иначе?
Эйнштейн разрешил это противоречие, критически анализируя операции, необходимые для синхронизации часов в разных точках пространства, и то, как этот процесс синхронизации изменяется при совокупном движении с постоянной скоростью. Из этого анализа следует, что время, приписываемое событию движущимся наблюдателем, отличается от времени, которое приписывает событию неподвижный наблюдатель, причем на величину, зависящую от положения этого события в пространстве. По отношению к одному и тому же событию время одного наблюдателя является смесью пространства и времени другого, и наоборот. Эта «относительность» пространства и времени – существенное новшество, которое специальная теория относительности Эйнштейна привнесла в физику. Оба предположения, лежащие в основе теории, уже были известны и были широко признаны до появления его работы, но никто не рассматривал их всерьез в совокупности и не добился их согласования.
Специальная теория относительности важна не только сама по себе, но также и потому, что она ввела в науку новую сверхидею для создания гипотез и уточнения наших физических законов, которая оказалась очень плодотворной и успешной. Эта сверхидея заключается в том, что мы назвали симметрией, поэтически определенной как Изменение без Изменения. Два постулата специальной теории относительности очень хорошо соответствуют этому описанию: первый говорит нам, какой вид изменений рассматривать (а именно – преобразования Галилея), а второй сообщает, что они не меняют (а именно – скорость света).
Тема симметрии, или инвариантности, – Изменения без Изменения – много раз и с разными вариациями звучит в нашей медитации. Сначала она робкая и приглушенная, но затем становится все более яркой и усиливается, пока в конце концов не оказывается господствующей в нашем самом глубоком понимании Природы.
Спин
Spin
В английском языке глагол to spin означает «вращаться», но можно также сказать, что объект обладает вращением (has spin), если он вращается вокруг некоторой оси. Вращение, или спин, имеет то же значение и в квантовом мире, но это понятие становится более важным в основном по двум причинам.
• Многие частицы никогда не перестают вращаться! Для этих частиц вращательное движение вокруг их центра – один из аспектов спонтанной активности, которая так характерна для квантового мира. Электроны, протоны и нейтроны – все обладают этим свойством. В какой бы момент мы ни измеряли угловой момент вращения, его величина окажется равна одной второй, умноженной на приведенную постоянную Планка. Мы говорим, что эти частицы имеют спин ? или являются частицами со спином ?.
• Многие частицы, в особенности электроны, действуют как небольшие магниты. Подобно Земле, они создают магнитные поля, структура которых согласована с направлением их вращения. Магнитное поле, связанное с одним-единственным электроном, довольно мало, но, если многие электроны выстроят свои оси вращения в одном направлении, их поля складываются. Магнетизм классических «магнитов» – по существу, стержней из железной руды – является результатом одинаковой ориентации полей вращающихся электронов, которые в них содержатся.
Спинорное представление
Spinor representation
Спиноры – своего рода усовершенствованная версия векторов. Они появляются в математическом описании спина электрона в уравнении Дирака как пространство свойств частиц вещества в схеме объединения SO (10) (Джорджи – Глэшоу), в общих чертах описанной в главе «Квантовая красота IV» и в нескольких других передовых направлениях физики. Описание математического аппарата спиноров далеко выходит за рамки этой книги, но я указал две легкодоступные ссылки в примечаниях в конце книги.
Спиральность
См. Четность.
Спонтанное нарушение симметрии
Spontaneous symmetry breaking
Между точным соблюдением симметрии и ее полным отсутствием существует промежуточная возможность, спонтанное нарушение симметрии, которое ощутимо присутствует в нашем описании мира.
Мы говорим, что наблюдается спонтанное нарушение системы уравнений, если:
• уравнения удовлетворяют симметрии, но устойчивые решения этих уравнений ей не удовлетворяют.
Таким образом находит оправдание наблюдаемая нехватка симметрии. Симметрия присутствует в уравнениях, но сами уравнения говорят нам о том, что мы не будем ее наблюдать!
Пример. В фундаментальных уравнениях, которые описывают кусок естественного магнита, любое направление в пространстве эквивалентно всем остальным. Но этот кусок представляет собой магнит, а в магните уже нельзя сказать, что все направления эквивалентны. Каждый магнит имеет полюса и может быть использован в качестве стрелки компаса. Объяснение того, как теряется (или «нарушается») вращательная симметрия, довольно простое, но глубокое. В магните существуют силы, которые стремятся выровнять спины электронов со спинами их соседей.
В ответ на действие этих сил все электроны должны выбрать общее направление, в котором им выстроиться. Силы, так же как и уравнения, которые описывают их, будут безразличны к выбору этого направления, но выбор должен быть сделан. Таким образом, устойчивые решения этих уравнений обладают меньшей симметрией, чем сами уравнения.
В нашей Главной теории слабого взаимодействия имеется вращательная симметрия между направлениями в слабом цветовом пространстве, которая спонтанно нарушается за счет существования заполняющего пространство поля Хиггса. Основная идея очень похожа на ту, которую мы только что рассмотрели, обсуждая обычный магнит. Так же, как фундаментальные уравнения для сил взаимодействия электронов побуждают спины соседних электронов выстраиваться в одном направлении, таким же образом фундаментальные уравнения побуждают поле Хиггса выравнивать свое направление в пространстве свойства слабого заряда между соседними точками пространства-времени. Общее направление должно быть выбрано, и, таким образом, симметрия вращения (в пространстве свойства слабого заряда) спонтанно нарушается.
Успех этих идей, предоставивших превосходное описание слабого взаимодействия, и предсказание существования частицы Хиггса поощряет нас и далее исследовать возможность того, что лежащая в основе всего симметрия уравнений нашего мира намного больше, чем та симметрия, которую мы наблюдаем в природе, рассматривая лежащие в основе еще более широкие группы симметрии.
Среда
Medium/media
Среда для нас – это что-то, заполняющее пространство[114].
Таким образом, понятие среда может использоваться наравне с понятием флюида. На полях отметим, что «флюид» предполагает некий материал, части которого могут меняться местами друг с другом, как в потоках воздуха или воды, в то время как «среда» предполагает нечто более осязаемое, которое может колебаться, но имеет структурную целостность, как стекло или желе. Но среды, или флюиды, которые, согласно нашей Основной теории, составляют наиболее фундаментальную материальную основу мира, – такие как глюонный флюид и электронный флюид, настолько отличаются от воздуха, воды, стекла, желе или любой другой привычной нам жидкости или среды, что кажется глупым настаивать на любой одной из двух метафор.
Стандартная модель
См. Главная теория.
Стационарное состояние
Stationary state
Исторически термин «стационарное состояние» возник в модели атома Бора. Если применять классическую механику и электродинамику к задаче об отрицательно заряженном электроне, связанном с положительно заряженным протоном, то стационарное решение найти нельзя. Электрон будет падать по спирали на протон, излучая электромагнитные волны. Чтобы избежать этой катастрофы, Бор ввел смелую гипотезу – гипотезу о стационарных состояниях. В ней электрону позволено занимать лишь немногие из классически разрешенных орбит, которые и определяют его разрешенные «состояния». В пределах этих особых орбиталей электрон не излучает энергию, а является «стационарным». Таким образом, разрешенные орбитали определяют стационарные состояния.
Впоследствии модель Бора была заменена современной квантовой механикой, но некоторые элементы первой, включая понятие стационарного состояния, можно увидеть и в современной теории. В современной квантовой теории состояние электрона описывается волновой функцией. Эта волновая функция и связанное с ней облако вероятности изменяются во времени согласно фундаментальному уравнению Шрёдингера. Среди решений уравнения Шрёдингера есть некоторые особые, у которых облако вероятности совсем не изменяется во времени. Эти решения – плод квантовой теории – имеют свойства, которые Бор постулировал для стационарных состояний в своей модели. Таким образом, в квантовой теории мы говорим, что волновые функции, чьи облака вероятности не изменяются во времени, определяют стационарные состояния. Повторим, что дополнительную информацию, включая иллюстрации, стоящие тысячи слов, см. в главе «Квантовая красота I», а также в статье о Спектрах.
Специальные волновые функции, которые определяют стационарные состояния (волновые функции, облака вероятности которых не изменяются во времени), являются чрезвычайно полезными при обдумывании задач в атомной физике и химии. Как дань их предшественницам, разрешенным орбитам Бора, их называют орбиталями.
Понятие о стационарности состояния является приблизительным, поскольку существуют физические процессы, с помощью которых электрон может совершить переход между этими состояниями. А именно электрон в стационарном состоянии может перейти в другое стационарное состояние, испустив или поглотив фотон. Бор не мог в пределах его модели разработать подробную картину или механизм для этого скачкообразного изменения орбиты и просто ввел его как дополнительное предположение: возможность квантовых переходов, или квантовых скачков.
В современной квантовой теории переходы между стационарными состояниями происходят как логическое следствие уравнений. Физически они возникают из-за взаимодействия между электронами и электромагнитным флюидом. Поскольку это взаимодействие довольно незначительно по сравнению с основными электрическими силами, которые удерживают электроны, нам нередко хорошо удается учесть его в модели как поправку, сохраняя стационарные состояния в качестве отправной точки. При таком подходе мы обнаруживаем, что переходы не являются истинными нарушениями непрерывности, хотя они действительно происходят быстро.
Процесс излучения особенно интересен с концептуальной точки зрения. В нем электрон порождает электромагнитную энергию в виде фотона там, где его первоначально не было. Это происходит, когда электрон сталкивается со спонтанной активностью в электромагнитном флюиде и, передавая ему часть собственной энергии, усиливает эту активность. Таким образом, электрон переходит в состояние с более низкой энергией, виртуальный фотон становится реальным фотоном, и да будет Свет.
Стоячая волна и бегущая волна
Standing wave/traveling wave
Колебания волн в ограниченных областях пространства называют стоячими волнами. Таким образом, колебания струн музыкальных инструментов – или их резонансных дек – являются стоячими волнами. Стоячие волны часто называют вибрациями или колебаниями.
Волны, которые не ограничены конечной областью пространства, а перемещаются в нем, называют бегущими волнами. В повседневном языке, а также и в физике, когда мы говорим о «звуковых волнах», мы обычно подразумеваем бегущие волны. Колебания резонансной деки рояля, которые являются стоячими волнами, толкают воздух рядом с ней взад и вперед. Движущийся воздух оказывает воздействие на воздух рядом с ним, который воздействует на воздух чуть дальше, и т. д., вызывая возмущение в воздухе, которое начинает жить собственной жизнью. Это бегущая звуковая волна, которую мы можем обнаружить, т. е. услышать, на больших расстояниях.
Волновая функция, связанная с электроном, может быть как стоячей волной, так и бегущей волной.
Волновую функцию электрона, связанного с протоном и образующего вместе с ним нейтральный атом водорода, считают стоячей волной даже при том, что, строго говоря, она распространяется по всему пространству. Дело в том, что плотность облака вероятности нахождения электрона, которая отражает величину волновой функции, уменьшается очень быстро, когда мы удаляемся от протона, и никогда не бывает значительной за пределами маленькой фиксированной области около протона. Именно это мы имеем в виду, когда говорим, что электрон связан с протоном. Фактически волновая функция локализована в ограниченной области пространства, и ее следует считать стоячей волной.
Волновая функция несвязанного электрона, который свободно перемещается в пространстве, является бегущей волной.
См. также Уравнение Шрёдингера.
Строгость
Rigor
Мы говорим, что утверждение строгое или обладает строгостью, когда оно одновременно точно сформулировано и его трудно оспорить. Мы называем некое понятие строгим, если его смысл точно сформулирован и, таким образом, оно подходит для использования в строгих утверждениях.
Сама «строгость» не является строгим понятием, потому что выражение «трудно оспорить» несколько туманно. (Насколько трудно?) Например, существует огромный массив данных, основанный на решениях уравнений квантовой хромодинамики (КХД) с использованием компьютеров, что эта теория воспроизводит явление конфайнмента кварков и правильно предсказывает спектр адронов. (Другими словами: вычисления правильно предсказывают существование ряда сильно взаимодействующих частиц, их массы и другие свойства; впрочем, кварков среди них нет.) Однако математики обычно не расценивают этот вывод как строгий.
Струя частиц
Jet of particles
После соударений в современных ускорителях высоких энергий, включая, в частности, Большой адронный коллайдер, часто наблюдаются потоки энергичных адронов, движущихся почти в одном и том же направлении. Такие потоки называют струями.
Для струй существует замечательная интерпретация, основанная на квантовой хромодинамике (КХД) и асимптотической свободе и состоящая в следующем. Мы можем описать начальный момент нашего соударения, в котором участвует сильное взаимодействие, непосредственно в терминах кварков, антикварков и глюонов. Но по мере того, как эти частицы рождаются из начального раскаленного шара, они приходят в равновесие с вездесущей самопроизвольной активностью квантовых флюидов КХД – их квантовыми флуктуациями, или виртуальными частицами – и в процессе этого производят потоки адронов. Поскольку энергия и импульс сохраняются, эти потоки наследуют их от кварков, антикварков и глюонов, которые их породили. Таким образом, скажем, кварк с высокой энергией породит поток адронов, движущихся как целое в направлении импульса кварка и делящих между собой его энергию, – т. е. он породит струю! Не будет большим преувеличением сказать, что, когда наблюдаем струи, мы краешком глаза можем взглянуть на реальность существования кварков, антикварков и глюонов, которые не могут существовать как свободные частицы. См. Конфайнмент.
Суперсимметрия
Supersymmetry
Суперсимметрия – это особый вид симметрии. Преобразования суперсимметрии включают в себя пространственную трансляцию (или сдвиг) в квантовом измерении. Когда частица взаимодействия (бозон) перемещается в квантовом измерении, она становится частицей вещества (фермионом), и наоборот.
Если мы сможем привыкнуть к мысли, что сила и вещество являются одной и той же сущностью, наблюдаемой с разных ракурсов, мы достигнем нового уровня единства и согласованности в нашем фундаментальном понимании Природы. В настоящее время, однако, свидетельства наличия суперсимметрии, хотя и впечатляющие, являются косвенными.
Темная энергия, темная материя
Dark energy/dark matter
Главная теория дает нам подробное, глубинное понимание практически всего вещества, которое мы можем найти на Земле и поблизости от нее. Это «нормальное» или «обычное» вещество состоит из u- и d-кварков, цветных глюонов, фотонов и электронов, а также относительно неплотного потока нейтрино. Однако астрономические наблюдения показывают, что Вселенная в целом содержит другие виды вещества, которые составляют большую часть ее общей массы. Природа этого дополнительного вещества в настоящее время точно не известна, но мы можем систематизировать известные факты в простом и показательном виде.
• Обычное вещество дает примерно 5 % от общей массы Вселенной. Оно очень неравномерно распределено в виде галактик (которые затем разделяются на газовые облака, звезды и планеты), а между ними имеются большие области, практически лишенные обычного вещества.
• Темная материя, известная также как скрытая масса, составляет около 27 % общей массы Вселенной. Она тоже распределена неравномерно, но не настолько, как обычное вещество. Астрономы обычно говорят, что галактики окружены более диффузными гало из темной материи, но с учетом соотношения их масс было бы более правомерно сказать, что галактики – это концентрированные вкрапления в облаках темной материи. Темная материя очень слабо взаимодействует с обычным веществом, включая и свет. Следовательно, она не темная в общепринятом смысле, а скорее прозрачная.
• Темная энергия составляет около 68 % общей массы Вселенной. Она распределена равномерно, как если бы была глобальной плотностью массы, связанной с самим пространством. Есть свидетельства того, что эта плотность была постоянна во времени, на протяжении миллиардов лет. Как и темная материя, темная энергия очень слабо взаимодействует с обычным веществом, и она скорее прозрачная, чем темная.
Выводы о существовании темной материи и темной энергии и об их распределении в пространстве сделаны в результате наблюдений за обычным веществом. Мы обнаруживаем, что во многих ситуациях в астрофизике и в космологии мы можем объяснить движение обычного вещества, используя известные законы физики (Главную теорию) только в том случае, если предположим существование дополнительных источников массы помимо обычного вещества. Другими словами, движение обычного вещества под действием его собственной гравитации по нашим расчетам не согласуется с его наблюдаемым движением.
Это расхождение в принципе может быть следствием несостоятельности общей теории относительности, но, несмотря на многие попытки, не удалось создать никакой другой привлекательной теории (даже если допустить здесь очень низкую планку «привлекательности»).
В попытках улучшить Главную теорию довольно независимо друг от друга были выдвинуты предположения о существовании новых форм материи, которые могли бы подойти на роль темной материи. Для этого годятся и аксионы, и новые частицы, предложенные теориями суперсимметрии: они достаточно стабильны и слабо взаимодействуют с обычным веществом. Более того, согласно расчетам, они могли бы быть рождены во время Большого взрыва примерно в нужном количестве, а также могли бы распределиться как раз так, как мы это наблюдаем. Эти возможности в данный момент являются предметом очень активных экспериментальных исследований.
Темная энергия имеет свойства, которых можно ожидать от «космологического члена» Эйнштейна, а также от плотностей энергии, связанных с полем Хиггса, спонтанной активностью квантовых полей и еще несколькими более или менее правдоподобными источниками. Возможно, что независимый вклад в темную энергию дают сразу несколько таких эффектов, причем какие-то могут вносить положительный, а какие-то отрицательный вклад в общую сумму. В отличие от ситуации с темной материей, существующие теоретические идеи о темной энергии расплывчаты, и их сложно фальсифицировать.
Здесь стоит заметить, что современная проблема темной материи и темной энергии имеет два выдающихся исторических прецедента. Трудоемкие работы в области небесной механики, основанной на теории гравитации Ньютона, к середине XIX в. выявили два небольших расхождения между расчетами и наблюдениями. Одно касалось движения Урана, другое – Меркурия. Проблема Урана была разрешена с помощью своего рода «темной материи». Урбен Леверрье и Джон Коуч Адамс предположили, что его избыточное ускорение вызвано гравитационной силой, исходящей от новой, до сих пор неизвестной планеты, чье положение они могли рассчитать. Необходимая планета – Нептун – была действительно обнаружена в нужном месте! Трудность с Меркурием разрешилась, когда общая теория относительности Эйнштейна заменила теорию гравитации Ньютона. Новая теория, предложенная совершенно по другим и более глубоким причинам, дала немного отличные предсказания для орбиты Меркурия, и ее предсказания согласуются с наблюдениями.
Доводы с антропным привкусом применялись как к проблеме темной энергии, так и к проблеме темной материи, причем аргументация строилась похожим образом в обоих случаях:
• Часть Вселенной, которую мы можем сейчас наблюдать, – всего лишь малая доля большей структуры, которую иногда называют мультивселенной. (Заметим, что с течением времени область, доступная для наблюдения, расширяется из-за конечной скорости света.)
• Физические условия в других, удаленных, частях мультивселенной могут разниться. В частности, плотность темной энергии, или темной материи, может быть другой.
• В областях, где плотность темной энергии или темной материи, резко отличается от того, что мы наблюдаем в нашей Вселенной, не может появиться разумная жизнь.
• Поэтому могут наблюдаться лишь такие значения этих плотностей, которые близки к наблюдаемым нами.
Второй и третий шаг этих рассуждений в настоящее время являются спорными, поэтому эти идеи остаются умозрительными. Но, поскольку наши знания о фундаментальных законах и наши способности постичь их следствия совершенствуются, с логической точки зрения возможно, что такие идеи станут общепринятыми. Если это случится, мне кажется, что эта цепочка рассуждений окажется убедительной. Это будет означать удивительное открытие: главные черты наблюдаемого нами мира – а именно плотности темной энергии и/или темной материи – определяются не абстрактными принципами динамики или симметрии, но отбором, вроде отбора в биологии.
Теорема (закон Гаусса)
Gauss's law
На самом деле существует две[115] теоремы Гаусса с очень похожими формулировками.
Согласно теореме Гаусса для электрического поля, поток электрического поля через любую замкнутую поверхность равен количеству электрического заряда, заключенного внутри этой поверхности.
Согласно теореме Гаусса для магнитного поля, поток магнитного поля через любую замкнутую поверхность равен нулю. Иначе говоря, этот поток равен количеству магнитного заряда, заключенного внутри этой поверхности, а такого заряда в Природе не обнаруживается.
Эти теоремы Гаусса увековечены в двух уравнениях Максвелла.
Теорема Пифагора
Pythagorean theorem
Теорема Пифагора была опережающим свое время поразительным открытием в геометрии. Теорема Пифагора гласит, что квадраты длин двух более коротких сторон прямоугольного треугольника составляют квадрат длины самой длинной стороны (гипотенузы). Она обсуждается подробно, с чертежами, в основном тексте.
Теория Янга – Миллса
Yang-Mills theory
В 1954 г. Чжэньнин Янг и Роберт Миллс открыли, как создать новый большой класс теорий, в которых глобальная симметрия пространства свойств обобщена до локальной симметрии. В их честь теории такого вида часто называют теориями Янга – Миллса. Наши Главные теории сильных и слабых взаимодействий включают в себя подобную конструкцию.
Переходя от специальной теории относительности к общей теории относительности в 1915 г., Эйнштейн обобщил галилееву симметрию от глобальной до локальной. Грубо говоря, Янг и Миллс научили нас, как сделать этот вид обобщения, от глобальной симметрии до локальной, для широкого класса возможных групп симметрии, применимых для частиц.
В основном тексте мы сравниваем переход от глобальной симметрии к локальной с переходом от обычной геометрической перспективы, которой занимается проективная геометрия, к более гибким возможностям анаморфного изображения.
Ток
Current
Электрический ток – мера движения электрического заряда из одного места в другое[116]. Самый простой, идеализированный случай электрического тока связан с движением одного электрона. В этом случае электрический ток равен электрическому заряду электрона, умноженному на его скорость, в мгновенном положении электрона и нулю в остальных точках пространства. Если скорость электрона остается постоянной, ток постоянен по величине, но его местоположение движется вместе с электроном.
В ситуации, когда у нас есть много электронов вместе с другими электрически заряженными частицами, полный электрический ток равен сумме всех электрических токов, вызванных каждой из этих частиц по отдельности (и во всех случаях это заряд, умноженный на скорость). Величина этого фундаментального «микроскопического» тока[117] определена в каждой точке пространства и в любой момент времени. Другими словами, электрический ток – это векторное поле.
Величина микроскопического электрического тока, определенная таким образом, строго равна нулю, если движущихся электрически заряженных частиц нет, и беспорядочно меняется в пространстве и времени. Обычно бывает удобно для практического применения усреднять величины по областям пространства, которые содержат множество электронов. Таким способом мы определяем усредненный электрический ток, который гладко меняется в пространстве и времени. Обычно при обсуждении электрических токов в электрических цепях или в электроприборах такое усреднение считается само собой разумеющимся.
Сходным образом мы можем говорить о токах, связанных с перемещением других видов зарядов, таких как два вида слабых цветовых зарядов слабого взаимодействия или трех сильных цветовых зарядов сильного взаимодействия. Также имеются (если заменить в определении «заряд» на «массу») массовые токи, связанные с перемещением массы, потоки энергии, связанные с перемещением энергии, и т. д. В общеупотребительном языке мы можем использовать слово «ток»[118] для описания потоков воды и при этом имеем в виду массовый ток.
Тон, чистый тон
Tone/pure tone
Выражение «чистый тон» в этой книге означает простое волновое возмущение, которое является периодическим как в пространстве, так и во времени. (Здесь слово «простое» имеет определенное техническое значение: форма волны является синусоидальной, но здесь я не буду останавливаться на этом подробно. В примечаниях в конце книги имеются две легкодоступные ссылки.)
Самые важные примеры чистых тонов для нас касаются звуковых волн и электромагнитных волн (включая главным образом свет). В звуковых волнах изменению подвергаются давление и плотность воздуха; в электромагнитных волнах – электрические и магнитные поля.
Глубокое и приятное озарение, которое приходит в результате научного исследования Природы, состоит в том, что чистые тона, определенные вышеприведенным математическим/физическим способом, соответствуют простым чувственным восприятиям. Чистые звуковые тона легко создать с помощью электроники, и они могут быть знакомы вам по проверкам слуха или благодаря примитивным устройствам электронной музыки (какие, например, иногда встраивают в поздравительные открытки) или по камертонам. Чистые визуальные тона – это спектрально чистые цвета, которые появляются в радуге или в солнечном свете, преломленном призмой, как в экспериментах Ньютона. Эти два взаимодополняющих взгляда на чистые тона – с точки зрения восприятия и с точки зрения научных концепций – красиво иллюстрируют столь желаемое нами соответствие
Реальное ? Идеальное.
Тона, которые издают более традиционные музыкальные инструменты, когда вы извлекаете единственную «ноту», далеки от чистых. Подробное описание изменяется от инструмента к инструменту, но во всех случаях нота содержит много чистых тонов, звучащих одновременно с различной силой. Самым мощным из них является чистый тон, который дает имя этой ноте, но качество музыкального звука, тембр, который отличает различные инструменты друг от друга, в значительной степени определяется дополнительными тонами, так называемыми обертонами.
Эта тема обсуждается более подробно в основном тексте. Также к этой теме имеет отношение словарная статья о Спектрах.
Трансляционная (сдвиговая) симметрия времени
Time translation symmetry
Трансляция или смещение во времени – преобразование, которое сдвигает времена событий на один и тот же временной интервал. Трансляционная симметрия времени – это гипотеза о том, что законы физики неизменны, или, как мы говорим, инвариантны, при таком преобразовании. Трансляционная симметрия времени – строгий способ сформулировать идею о том, что законы физики одинаковы на протяжении всей истории. Трансляционная симметрия времени тесно связана с сохранением энергии через теорему Эмми Нётер.
Трансляционная (сдвиговая) симметрия пространства
Spatial translation symmetry
Пространственная трансляция (или параллельный перенос, или сдвиг) – преобразование, которое изменяет положение точек в пространстве на одинаковое смещение. Трансляционная симметрия пространства – это гипотеза о том, что законы физики неизменны или, как мы говорим, инвариантны, при таком преобразовании. Трансляционная симметрия пространства – строгий способ сформулировать идею о том, что законы физики одинаковы повсюду. Трансляционная симметрия пространства тесно связана с сохранением импульса через теорему Эмми Нётер.
Трансляция (сдвиг)
Translation
Смещение всех точек системы на одну и ту же величину в пространстве или во времени. См. Трансляционная (сдвиговая) симметрия пространства и Трансляционная (сдвиговая) симметрия времени.
Угол Кабиббо
См. Семейство.
Уравнение Дирака
Dirac equation
В 1928 г. Поль Дирак (1902–1984) предложил динамическое уравнение, описывающее поведение электронов в квантовой механике, которое мы теперь называем уравнением Дирака. Уравнение Дирака уточняет более раннее уравнение Шрёдингера для электрона примерно так же, как уравнения Эйнштейна для механики уточняют уравнения Ньютона. В обоих случаях новые уравнения согласуются со специальной теорией относительности, в то время как те более простые, которые они заменили, с ней не согласуются. (И в обоих случаях новые уравнения повторяют предсказания старых при описании поведения тел, движущихся со скоростями, много меньшими скорости света.)
Уравнение Дирака имеет дополнительные решения, кроме тех, что представляют электроны в разных состояниях движения (и спина). Эти решения описывают частицы с такой же массой, как у электронов, но с противоположным электрическим зарядом. Эти новые частицы называются антиэлектронами, или позитронами. Позитроны были экспериментально открыты в 1932 г. Карлом Андерсоном благодаря изучению космических лучей. См. также Антивещество.
Уравнение Дирака, с соответствующими (относительно незначительными) изменениями, описывает не только поведение электронов, но также и поведение других фундаментальных частиц со спином ?, включая все кварки и лептоны, – другими словами, частиц вещества, как они именуются в основном тексте. С немного более значительными изменениями оно также описывает поведение адронов со спином ?, включая протоны и нейтроны.
Уравнение Шрёдингера
Schr?dinger equation
Уравнение Шрёдингера было предложено Эрвином Шрёдингером (1887–1961) в 1925 г. Это динамическое уравнение, которое определяет, как волновые функции электронов или других частиц изменяются во времени.
Уравнение Шрёдингера является приблизительным в двух важных отношениях. Во-первых, оно основано на нерелятивистской (ньютоновской) механике, а не на релятивистской механике Эйнштейна. Поль Дирак в 1928 г. предложил другое уравнение для волновых функций электронов, которое подчиняется положениям специальной теории относительности (см. Уравнение Дирака). Во-вторых, оно не включает влияние квантовых флуктуаций, таких как виртуальные фотоны, на электроны. Тем не менее уравнение Шрёдингера достаточно точно для большинства практических применений квантовой теории в химии, материаловедении и биологии, и это именно та версия квантовой теории, которая обычно применяется при обсуждении этих дисциплин.
Хотя обычно говорят об «уравнении Шрёдингера», но Шрёдингер предоставил нам не просто одно уравнение, а скорее процедуру для вывода уравнений, описывающих различные ситуации, в которых применима квантовая механика.
Одно из самых простых уравнений Шрёдингера – уравнение для единственного электрона, который испытывает электрическое притяжение единственного протона. Это дает нам описание атома водорода. Хотя оно сформулировано в ином пространстве идей – в мире, где заполняющие пространство волновые функции заменяют собой частицы, двигающиеся по орбитам, – результаты, которые вытекают из уравнения Шрёдингера в этом случае, в значительной степени подтверждают интуитивную концепцию Бора о значении спектра водорода. Обзор этого вопроса см. в статье Спектры.
Мы можем также сформулировать уравнения Шрёдингера, которые описывают поведение нескольких электронов одновременно. Разумеется, мы должны сделать это, если хотим учесть влияние электронов друг на друга. Как объясняется в словарной статье о волновой функции, волновые функции, которые полностью описывают физическое состояние нескольких электронов, определены в пространствах очень высокой размерности. Волновая функция для двух электронов «обитает» в шестимерном пространстве, волновая функция для трех электронов – в девятимерном пространстве и т. д. Уравнения для этих волновых функций быстро становятся довольно трудными для решения, даже приблизительного и даже с использованием самых мощных компьютеров. Вот почему химия остается процветающим экспериментальным полем деятельности, несмотря на то, что в принципе мы знаем уравнения, которые ей управляют и которые должны позволять нам вычислять результаты химических экспериментов без необходимости выполнять их.
Уравнения Максвелла
Maxwell's equations
Уравнения Максвелла – система из четырех уравнений, которые выражают зависимости между электрическими полями, магнитными полями и распределениями электрического заряда и электрического тока в пространстве. Они всесторонне обсуждаются в тексте и примечаниях.
См. также статьи Закон Ампера (Закон Ампера – Максвелла), Закон Фарадея и Закон Гаусса, где четыре уравнения Максвелла объясняются по отдельности.
Ускорение
Acceleration
Скорость – это быстрота изменения местоположения со временем (см. Скорость), а ускорение – это быстрота изменения скорости со временем. Одним из великих достижений Ньютона было то, что он показал: ускорение тел связано с действующими на них силами. (Он провозгласил это открытие прежде полного описания с помощью памятной анаграммы, как описано в главе «Ньютон III».) В старых учебниках по классической механике встречается второй закон движения Ньютона в такой формулировке: «Сила равна массе, умноженной на ускорение». При отсутствии какой-либо отдельной информации о силах это, конечно, бессмысленное утверждение. На самом деле его нужно интерпретировать как обещание о том, что изучение ускорения не будет напрасным!
Ньютон сделал несколько общих утверждений о силах. Примечателен его первый закон движения, который гласит, что «свободные» тела имеют нулевое ускорение, т. е. что скорость свободного тела постоянна. В этом законе подразумевается, что тела, удаленные от всех других тел, можно приближенно считать свободными или, другими словами, что силы убывают с расстоянием.
Ньютон также разработал подробную теорию одного вида сил, а именно – гравитационной силы. В этом контексте интересно заметить, что сила притяжения, действующая на тело, пропорциональна его массе, так что гравитационное ускорение не зависит от массы этого тела. Этот закон был проверен для случая земного притяжения в знаменитом опыте Галилея, в котором он сбрасывал предметы с наклонной («падающей») Пизанской башни.
В теории гравитации Эйнштейна, известной как общая теория относительности, закон движения выражается напрямую через ускорение, без дополнительного упоминания сил.
Ускорение, как и скорость, – это векторная величина.
Ускоритель
Accelerator
Ускоритель заряженных частиц – это установка для получения пучков быстро движущихся частиц с высокой энергией. В истории, да и в наши дни ускорители использовались для открытия фундаментальных процессов в природе. Изучая столкновения самых быстрых частиц, мы можем получить представление об их поведении при предельно высоких энергиях, малых расстояниях и коротких временах, которое невозможно добыть другими способами.
Фальсифицируемая теория, сильная теория
Falsifiable theory/powerful theory
Когда утверждение (или теорию) можно сравнить с эмпирическими наблюдениями и тем самым потенциально опровергнуть, мы говорим, что оно фальсифицируемо. Сэр Карл Поппер (1902–1994) выступал за то, чтобы фальсифицируемость служила критерием для того, чтобы отличать науку от другой деятельности человека. Хотя это и воодушевляет, я не думаю, что критерий фальсифицируемости Поппера адекватно отражает научную практику, так как зачастую мы больше заботимся о том, чтобы подтвердить хорошие идеи, а не отбросить плохие.
Фальсифицируемость больше подходит в качестве (частичного) критерия зрелости и плодовитости теорий, чем их принадлежности к науке или ненауке. В этом контексте фальсифицируемость должна рассматриваться вместе с силой. Теории, которые дают много успешных предсказаний, но также иногда терпят неудачи (например, практическая метеорология) или чьи предсказания в некоторых случаях по своей природе являются статистическими и, следовательно, не так просто фальсифицируемы (например, квантовая теория), могут тем не менее быть очень ценными и должны считаться научными согласно любому разумному определению этого термина.
Нельзя считать сильную, но несовершенную теорию просто ошибочной; скорее следует – пока не доказано обратное – считать ее многообещающей основой для усовершенствования. Ньютоновская (нерелятивистская) механика, классическая (не квантовая) теория электромагнетизма и другие, менее значительные теории были фальсифицированы, и все же мы их чтим, и у нас есть на это хорошие причины:
• Они остаются полезными благодаря их предсказательной силе и относительной простоте.
• Теории, которые пришли им на смену, во многом полагаются на их понятийный аппарат.
• В рамках более новых теорий прежние продолжают существовать в качестве приближений, верных в предельных случаях.
См. также Непротиворечивость и противоречие, Экономность (идей).
Фермион
См. Бозоны и фермионы.
Флюид
См. Поле и флюид.
Фотон и соотношение Планка – Эйнштейна
Photon/Planck – Einstein relation
Фотон – это минимально возможное возмущение электромагнитного флюида.
В классической физике в соответствии с уравнениями Максвелла энергия электромагнитной волны может быть сколь угодно малой. В квантовой теории дело обстоит иначе. Энергия существует только в виде дискретных единиц, или квантов. Поскольку эти единицы не могут быть разбиты на более мелкие, они обладают некоторой целостностью, которую мы обычно связываем с частицами, и в некоторых обстоятельствах бывает полезно думать о них именно так. В этом смысле фотоны – частицы света.
(Квантово-механическое описание фотонов не соответствует в точности ни классической идее волны, ни классической идее частицы. Нет причин, по которым эти идеи, почерпнутые из повседневного опыта с большими телами, были бы полноценным описанием того, что происходит в незнакомом царстве очень малых тел, и они таковым и не являются. Любой из двух подходов может быть полезным, но ни один из них в отдельности не отражает надлежащим образом действительность. См. Дополнительность.)
Для чистых спектральных цветов существует простая количественная связь между единицей энергии – т. е. энергией одного фотона – и частотой, связанной с электромагнитными волнами этого цвета. Она была предложена теоретически Планком и Эйнштейном в самом начале XX в. и названа соотношением Планка – Эйнштейна. Соотношение Планка – Эйнштейна сохранилось с тех пор без существенных изменений. Оно также имеет важное применение, которое является центральным в нашей медитации и помогает нам ответить на наш Вопрос.
Вот оно: энергия фотона равна частоте света, представителем которого он является, помноженной на константу Планка.
А вот как мы используем его: когда атом испускает или поглощает фотон, он совершает переход между двумя стационарными состояниями. Поскольку в этом процессе энергия сохраняется, энергия фотона соответствует разнице энергий этих двух устойчивых состояний. Таким образом, в спектре атома закодированы энергии его возможных состояний.
Подробнее об этом замечательном соотношении см. Спектры.
Фракталы
Fractals
Фракталы – это геометрические объекты, имеющие структуру на всех масштабах. Если вы увеличиваете сложное изображение фрактала, чтобы лучше рассмотреть его детали, вы обнаруживаете, что каждая деталь настолько же сложна, как исходное целое изображение, – более того, во многих фракталах увеличенная часть идентична целому изображению!
Существует множество разнообразных фракталов. Нет такого единственного строгого определения, которое было бы применимо ко всем объектам, которые люди называют «фракталами». Вместо этого есть огромное количество интересных примеров, воплощающих эту широкую концепцию неисчерпаемой внутренней структуры.
Поскольку небольшие части фрактала настолько же сложны, как и целый фрактал, метод Анализа и Синтеза и его классическая математическая реализация, дифференциальное и интегральное исчисление, теряет большую часть своих возможностей. В игру вступают другие идеи, основанные на рекурсии и самоподобии. (Я остановлюсь здесь: хотя эти идеи завораживающи, они довольно слабо связаны с нашими основными темами.)
Очень сложные фракталы можно создать, следуя простым правилам много шагов подряд – такой метод прекрасно подходит для компьютерной графики. Это привело к получению потрясающих изображений и появлению новых форм изобразительного искусства.
Фуллерен (бакибол)
Buckminsterfullerene[119]
Фуллерены – это класс молекул чистого углерода.
Они принимают форму квазисферических многогранников, в которых каждое из ядер углерода имеет химические связи с тремя ближайшими соседними ядрами. В число граней всегда входят 12 пятиугольников плюс переменное (обычно большее) число шестиугольников. Особенно распространен фуллерен C60, содержащий 60 ядер углерода. Молекулы C60 часто называют бакиболами, отмечая их необъяснимое сходство с (микроскопическими) футбольными мячами.
См. также Многоугольник.
Функция
Function
Когда какая-то величина меняется со временем, мы говорим, что это функция времени. Более общо, мы говорим, что величина y является функцией некоторой другой величины x, если каждое значение x определяет некоторое значение y. Мы пишем y (x) для величины y, определяемой величиной x.
Примеры:
• Температура в Бостоне является функцией времени.
• Температура на поверхности Земли, вообще говоря, является функцией положения на поверхности и времени. Другими словами, это функция пространства-времени.
См. также Поле.
Цвет света, спектральный цвет
Color of light/spectral color
Размышляя о свете, важно различать физический цвет и воспринимаемый цвет.
Спектральный цвет – это физическое понятие, не зависящее от человеческого восприятия. В принципе его можно определить и исследовать, используя только физические приспособления: линзы, призмы, фотопластинки и т. д. Мы можем создать свет любого чистого спектрального цвета, пропустив пучок белого света через призму и выбрав небольшую часть получившейся «радуги», как это описано в основном тексте. Сейчас мы понимаем, что чистые спектральные цвета соответствуют электромагнитным волнам, которые колеблются с определенной частотой. Различные чистые спектральные цвета строго соответствуют различным частотам. Согласно (хорошо проверенной) теории Максвелла, можно получить электромагнитную волну с какой угодно частотой, так что чистые спектральные цвета образуют непрерывный спектр. Человеческий глаз чувствителен только к электромагнитным волнам в узком диапазоне частот; но часто бывает естественно говорить о «свете» в более общем значении, включая в это понятие электромагнитные волны в виде радиоволн, микроволнового, инфракрасного, ультрафиолетового, рентгеновского и гамма-излучения. Полный диапазон возможных частот образует электромагнитный спектр.
Спектральные цвета похожи на чистые тона в музыке. Действительно, чистые тона тоже являются колебаниями – звуковыми волнами – с определенными частотами. Развивая эту аналогию, можно сказать, что белый свет соответствует какофонии тонов, что способствовало появлению термина «белый шум».
Концепция воспринимаемого цвета включает в себя смесь физики и психологии. Наши самые богатые цветовые впечатления, например, те, что мы получаем от изобразительного искусства, необычайно сложны и задействуют высокоуровневые процессы мозга, которые мы плохо понимаем. Тем не менее некоторые основные факты о ранних стадиях зрительного восприятия твердо установлены, и они уже подчеркивают огромный разрыв между анализом света, который возможен согласно основным физическим принципам, и тем анализом, который обеспечивает наше восприятие цвета. Самое главное отличие в следующем: в то время как чистые спектральные цвета образуют континуум, а полный анализ входящего света дает интенсивности каждого из них, человеческий глаз извлекает только три средних значения от этих интенсивностей.
Для куда более подробного изложения этих тем, которые являются центральными в нашей медитации, смотрите основной текст!
Цветовой заряд, сильный цветовой заряд, слабый цветовой заряд
Color charge/strong color charge/weak color charge
Наши Главные теории слабого и сильного взаимодействий строятся на идеях, впервые развитых в электродинамике. В частности, в них встречаются аналоги электрического заряда, называемые цветовыми зарядами. Заряды во всех случаях являются сохраняющимися величинами, которые управляют поведением фотоноподобных частиц – фотонов в случае электрического заряда, цветных глюонов в случае сильных цветовых зарядов, виконов в случае слабых цветовых зарядов.
Существует три сильных цветовых заряда – в нашей книге они называются красным, зеленым и синим. Восемь цветных глюонов реагируют на эти заряды и вызывают их преобразования.
Существует также два слабых цветовых заряда – в тексте они называются желтым и фиолетовым.
Не стоит и говорить (но однако скажу), что понятие «цвет», используемое в контексте цветового заряда, полностью отличается от понятия «цвет» в контексте света.
Циркуляция
Circulation
Векторные поля независимо от их истинной природы могут с математической точки зрения рассматриваться как поток обычной текучей среды, такой как воздух или вода. (Воображаемый поток в каждой точке имеет скорость, пропорциональную величине векторного поля в этой точке.) В такой модели циркуляция векторного поля в некоторой точке – это мера углового движения жидкости (газа). Так, например, циркуляция атмосферы особенно велика вблизи контуров, окружающих центр торнадо.
Давайте определим это понятие более точно. Представим, что наш контур есть осевая линия воображаемой узкой цилиндрической трубки, и посчитаем количество воздуха, которое перемещается по этой трубке за единицу времени, отнеся его к площади сечения трубки. (Потоком воздуха снаружи внутрь трубки или из нее наружу мы просто пренебрегаем.) Тогда мы получим циркуляцию потока по замкнутому контуру[120].
Используя аналогию потока – т. е. рассматривая электрическое поле как поле скоростей, мы можем похожим образом определить циркуляцию электрического поля или магнитного поля по замкнутому контуру. Эти величины являются главными участниками уравнений Максвелла. См. закон Ампера (закон Ампера – Максвелла) и закон Фарадея.
Здесь я хотел бы добавить личную коду, сочетающую в себе поклонение героям и эстетику. Новаторские статьи Фарадея и Максвелла, где впервые появилось представление об электромагнетизме как о поле, по большей части написаны с точки зрения словесных определений и ментальных образов, подобно тому, как я сделал это здесь для циркуляции и ниже – для потока, а не в виде общепринятых математических уравнений. Четко держать в голове такие сложные картины и проводить между ними связи было удивительным подвигом зрительного воображения, который показался мне достаточно вдохновляющим и прекрасным, чтобы его повторить. Представление уравнений в виде образов переносит их в ту область опыта, для наслаждения которой люди хорошо подготовлены.
Цифровой
Digital
Если величина не может изменяться плавно, мы называем ее цифровой величиной. Чтобы узнать больше об этом понятии, см. статью про аналоговые величины.
Частица вещества
Substance particle
Это еще одно название для всех фермионов. В Главной теории это кварки и лептоны.
Если суперсимметрия верна, то для каждой частицы вещества существует соответствующий «партнер» – частица взаимодействия. Частица вещества, перемещаясь в квантовом измерении, становится своей сопряженной частицей взаимодействия.
Частица взаимодействия
Force particle
«Частица взаимодействия» – это разговорная фраза, которую я использую, когда говорю, собирательно, о фундаментальных частицах Главной теории, которые являются бозонами: о фотоне, о виконе, о цветном глюоне, о гравитоне и о частице Хиггса. Это сделано для облегчения жизни читателя, а также для того, чтобы передать некоторую общую идею о роли этих частиц в Природе[121].
Частица Хиггса, бозон Хиггса
Higgs particle/Higgs boson
Эти термины взаимозаменяемы и используются для обозначения наименьшей единицы, или кванта, флюида Хиггса.
См. Поле Хиггса, флюид Хиггса, а также подробное обсуждение в главе «Квантовая красота III», часть 3.
Частота
Frequency
Если у нас есть процесс, который повторяется во времени, его период – это время между повторениями, а его частота – это единица, деленная на период, или, что то же самое, величина, обратная периоду. Таким образом, высокочастотный процесс – это процесс, который часто повторяется. Частоты измеряются в обратных секундах – единицах, также называемых герцами в честь Генриха Герца, первооткрывателя электромагнитного излучения.
Примеры: если процесс повторяется каждые 2 секунды, его частота равна 0,5 герца. Если процесс повторяется дважды в секунду – то его частота равна 2 герцам. Молодые здоровые люди способны слышать колебания воздуха, или звуковые волны, если частоты этих колебаний лежат в интервале примерно от 20 до 20000 герц. Человеческий глаз чувствителен к электромагнитным волнам с частотами от 4 ? 1014 до 8 ? 1014 герц – это довольно высокая скорость колебаний!
Четность, преобразование четности, нарушение четности и спиральность
Parity/parity transformation/parity violation/handedness
В нескольких разделах математики и при формулировке некоторых физических законов находят удобным использовать правую руку (или, гораздо реже, левую).
В большинстве случаев эти «правила правой руки» являются просто результатом соглашений. Соответствующее правило левой руки также можно было бы использовать, и это просто привело бы к переименованию вещей. Возьмите, например, способ, с помощью которого мы присваиваем определенное направление в пространстве вращению вокруг оси. Если объект вращается вокруг оси, мы можем присвоить оси направление, используя правило правой руки, как описано далее. Вообразите наш вращающийся объект как фигуристку на льду. Ось, вокруг которой она вращается, является прямой линией от ее головы до больших пальцев ног. Эта линия имеет некоторую ориентацию в пространстве и, таким образом, почти определяет направление, но, чтобы завершить его, нам нужен еще один шаг: мы должны выбрать между направлением «вверх» и «вниз». Обычное правило правой руки, призванное разрешить эту неоднозначность, говорит, что, если при вращении ее правая рука движется вперед, по направлению к животу, мы выбираем направление «вверх» – т. е. направление от ног к голове, в то время как, если вращение сопровождается движением ее правой руки назад, к спине, мы выбираем направление «вниз». Ясно, что, если бы мы поменяли правое с левым и, одновременно, в правиле, поменяли верх и низ, результирующее «правило левой руки» было бы полностью равнозначным.
Вот еще два примера использования этого правила:
• Движение стрелок часов выражается в их вращении относительно оси, перпендикулярной циферблату. Если вы смотрите на циферблат часов сверху вниз, то применение правила правой руки ко вращению стрелок «по часовой стрелке» дает направление вниз.
• Чтобы закрутить стандартный винт на свое место мы должны заставить его вращаться вокруг своей оси. Если мы смотрим сверху на винт, то мы должны вращать его по часовой стрелке, чтобы заставить его закручиваться вниз. Это срабатывает, поскольку стандартный, хороший винт нарезан так, чтобы соответствовать предыдущему правилу правой руки, и поэтому мы называем его винтом с правой резьбой. Другой вид, назовем их плохими винтами, имеют левую резьбу.
Во всех этих случаях мы могли бы прекрасно заменить правое на левое, чтобы описать точно те же самые ситуации. Нам нужно только поменять в этих определениях местами слова «по часовой стрелке» и «против часовой стрелки» и «хороший» и «плохой».
Точно так же в учебниках физики вы найдете много правил правой руки, описывающих, как определить направление магнитных полей и сил, создаваемых магнитными полями. Но если бы вы изменили правое на левое и одновременно изменили определение направления магнитного поля с точностью до наоборот, то в законах физики ничего бы не изменилось.
Физики полагали до 1956 г., что все проявления правого и левого в физике являются предметом простых соглашений – т. е. соглашениями о том, как определять понятия, принятыми просто для удобства. Соглашения могут быть очень полезными. Очень важно, например, быть в состоянии объяснить производителям винтов, каким образом нарезать резьбу. Но такие договоренности не принадлежат к фундаментальным принципам. Можно было принять другие соглашения!
Другой способ сформулировать это предположение, который красиво находит ему место в главном русле глубоких размышлений об основных принципах, – это предположение о симметрии. Мы говорим, что система уравнений имеет симметрию четности или они являются инвариантными относительно преобразований четности, если в них можно поменять местами левое и правое, сделав соответствующие изменения в определениях, и при этом содержание уравнений не изменится.
(Сделаем техническое дополнение, являющееся одновременно забавным упражнением. «Поменять левое и правое» требует некоторого более подробного объяснения, потому что левое и правое – это свойства объектов [например, рук], расположенных в пространстве, и мы не можем просто так переделать все левые руки в правые руки, все винты с левой резьбой в винты с правой резьбой и т. д., не сделав изменений в самом пространстве так, чтобы преобразованные объекты продолжали подходить друг другу! Проще всего сделать это если выбрать одну точку O – начало координат – и преобразовать любую точку в ее антипод относительно O. Таким образом, вы перемещаете любую точку P в точку диаметрально противоположную относительно точки O.)
Когда мы выполняем наше преобразование четности, отражая точки в их антиподы, естественно, что векторы изменят свое направление. Например, хорошим упражнением будет мысленно увидеть, что вектор, идущий из точки A в точку B, смотрит в противоположном направлении относительно вектора, нарисованного между их антиподами, из точки ?A в точку ?B.
Вот забавное упражнение с той же идеей: расположите большой палец и два следующих пальца правой руки, чтобы они указывали в трех взаимно перпендикулярных направлениях, сделайте затем то же самое с вашей левой рукой и расположите руки так, чтобы соответствующие пальцы двух рук указывали в противоположные стороны[122]. Посредством этого упражнения вы воплощаете преобразование четности: ваши пальцы указывают направления, и инверсия всех трех направлений преобразует левую руку в правую и обратно!
В 1956 г. Чжэндао Ли (род. 1926) и Чжэньнин (Фрэнк) Янг (род. 1922) после анализа некоторых озадачивающих экспериментов предположили, что, хотя большинство проявлений «рук» в физике, включая правила правой руки, которые запутывали поколения студентов, изучающих магнетизм, является вполне условным, слабое взаимодействие отличается в этом отношении и действительно делает различие между левым и правым. Другими словами, они предположили, что симметрия четности соблюдается не строго. Или же, если сказать коротко и просто, они предположили нарушение четности. Их предположение вскоре подтвердилось экспериментально, и этот прорыв привел к гораздо лучшему пониманию слабого взаимодействия.
Сегодня мы признаем, что нарушение четности – главная особенность слабого взаимодействия и важная часть формулировки соответствующего раздела Основной теории. Слабое взаимодействие делает большое различие между левым и правым, от которого нельзя избавиться за счет определений!
Чтобы точно установить различие, мы должны ввести спиральность частицы. Когда частица со спином еще и движется, мы имеем два направления, связанные с ней: направление, связанное с ее спином, которое мы определили ранее, и направление ее скорости. В определении направления, связанного со спином, мы использовали правило правой руки. Соответственно, если направление спина частицы, определенное таким образом, совпадает с направлением ее скорости, мы говорим, что это правая частица. В ином случае, если направление спина частицы противоположно направлению ее скорости, мы говорим, что это левая частица.
Подготовившись таким образом, мы теперь готовы описать, как слабое взаимодействие нарушает четность: левые кварки и левые лептоны, а также правые антикварки и антилептоны участвуют в слабом взаимодействии, но частицы с противоположной спиральностью этого не делают.
Наконец, позвольте мне выполнить обещание, сделанное в статье об аксиальном векторе, и дать определение этого термина. Выше мы видели, что векторы, связанные с движением из одной точки в другую, изменяют направление после преобразования четности. Векторы, которые преобразовываются подобным образом, называют истинными векторами, или полярными векторами. Однако не все векторы ведут себя таким образом! Векторы, в определение которых входит правило правой руки, поменяют направление дважды, если мы делаем преобразование четности: один раз, потому что они векторы, а второй раз, потому что они были определены «неправильным» для преобразованной системы правилом (потому что правое превратилось в левое!). Векторы, направление которых не изменяется, когда мы выполняем преобразование четности, называют псевдовекторами, или аксиальными векторами. Например, магнитное поле в физике – это поле аксиальных векторов.
Чистый тон
См. Тон, чистый тон.
Экономность идей
Economy of ideas
Мы называем объяснение или, в более общем случае, теорию экономной, если она содержит мало допущений, а объясняет многое.
Хотя она не включает обмена товарами или услугами, эта концепция не полностью лишена связи с настоящей экономикой. В ее рамках мы бы сказали, что разумное использование ограниченных ресурсов для создания ценной продукции – экономное использование этих ресурсов, так что это похожая идея.
Интуитивно кажется обоснованным предпочитать экономные объяснения их противоположностям – объяснениям, которые требуют многих допущений для объяснения ограниченного ряда фактов или наблюдений. Этот интуитивный подход находит поддержку в байесовской статистике, которая уверяет нас в том, что более экономное из двух объяснений с большей вероятностью является правильным, если оба одинаково хорошо объясняют одни и те же данные.
Электрический заряд
Electric charge
В современной физике и особенно в нашей Главной теории электрический заряд – первичное свойство вещества, которое не может быть объяснено чем-то более простым. Электрический заряд – это дискретная (цифровая) сохраняющаяся величина, на которую реагируют электромагнитные поля.
Самое простое проявление электрического заряда – его способность порождать силы. Согласно закону Кулона, две электрически заряженные частицы испытывают электрическую силу, пропорциональную произведению их электрических зарядов (и обратно пропорциональную квадрату расстояния между ними). Если заряды одного знака, то это между ними действует сила отталкивания, но она является силой притяжения, если заряды имеют противоположный знак. Следовательно, существует сила электрического отталкивания между двумя протонами, как и между двумя электронами, и сила электрического притяжения между протоном и электроном.
Электрический заряд всегда является кратным заряду протона. Электроны по отношению к протонам несут равный, но противоположный по знаку заряд. (Теоретически кварки обладают дробным зарядом относительно заряда протона. Однако кварки не появляются в виде отдельных частиц, а только в составе адронов. Электрические заряды адронов всегда являются кратными заряду протона.)
Электрический ток
См. Ток.
Электрическое поле, электрический флюид
Electric field, electric fluid
Величина электрического поля в любой точке определяется отношением электрической силы, которую испытывает заряженная частица, расположенная в этой точке, к электрическому заряду. Сила – это векторная величина, поэтому электрическое поле – векторное поле.
Это определение широко используется в молекулярной биологии, химии, электротехнике и других прикладных науках. Но в приложении к фундаментальной физике, где квантовые флуктуации становятся значительными, оно становится проблематичным, поскольку и силы, и положения частиц флуктуируют. Его можно оставить как приближенное представление, произведя тем или иным способом усреднение по времени и пространству.
В фундаментальной физике оказался полезнее другой подход, который избегает этих трудностей. Мы не настаиваем, что понятия, которые мы используем, соответствуют на всех этапах наблюдаемым величинам. Мы хотим, чтобы все наблюдаемые величины появлялись где-то в уравнениях, но мы можем считать – и мы считаем – удобным включить туда что-то другое кроме них! (См., в частности, статью о перенормировке.)
В таком ключе я определяю электрический флюид как заполняющее пространство активное нечто, появляющееся в уравнениях Максвелла.
Необходимость разделять понятия электрического поля и электрического флюида становится кристально ясной, если мы подумаем, как должны интерпретировать утверждение «Электрическое поле в межгалактическом пространстве исчезает». Это утверждение имеет смысл (и приближенно верно), если принять наше определение электрического поля через средние значения сил, которые оно создает. Однако будет совершенно неверно сказать, что квантово-механическая сущность, которая фигурирует в уравнениях Максвелла и проявляет спонтанную активность, где-либо исчезает. Поэтому обычная терминология, которая не различает эти два понятия – сущность саму по себе и ее среднее значение, – порочна в своей основе. (Этот порок, похоже, не слишком волнует большинство физиков, но он беспокоит меня!) Мы решаем эту проблему, называя саму сущность электрическим флюидом, а ее среднее значение электрическим полем.
(С учетом этого, если нет опасности запутаться, я буду иногда использовать термин «электрическое поле» как для сущности, так и для ее среднего значения. Вредные привычки изживаются с трудом.)
См. также Квантовый флюид.
Электричество
Electricity
«Электричество» – это общий термин, который используется для обозначения широкого спектра явлений, связанных с влиянием и поведением электрических зарядов.
Электродинамика, электромагнетизм
Electrodynamics/electromagnetism
Эти два термина взаимозаменяемы и используются для обозначения раздела науки, который описывает электричество, магнетизм и связь между ними.
Еще со времен работ Фарадея и Максвелла люди поняли, что электричество и магнетизм неразрывно связаны друг с другом. Меняющиеся во времени магнитные поля создают электрические поля, согласно закону Фарадея, а меняющиеся во времени электрические поля создают магнитные поля, согласно закону Максвелла (см. слагаемое Максвелла). Электромагнитные волны, возникающие из взаимосвязи этих законов, содержат как электрические, так и магнитные поля.
Из специальной теории относительности мы узнаем, что преобразования Галилея преобразуют электрические и магнитные поля (и флюиды) друг в друга.
Электромагнитная волна
Electromagnetic wave
Когда мы объединяем закон Фарадея, по которому меняющиеся магнитные поля создают электрические поля, с законом Максвелла, по которому меняющиеся электрические поля создают магнитные поля, мы обнаруживаем возможность самоподдерживающейся активности в этих полях. Эта самоподдерживающаяся активность принимает форму поперечных волн, которые перемещаются в пространстве со скоростью света. Мы называем эти волны электромагнитными волнами.
Максвелл открыл возможность существования электромагнитных волн и рассчитал их скорость. Обнаружив, что она совпадает со скоростью света, он предположил, что свет состоит из электромагнитных волн. По сей день это остается нашим фундаментальным описанием света.
Видимый свет соответствует только небольшой полосе электромагнитного спектра, который включает электромагнитные волны со всеми возможными длинами волн. Сейчас мы знаем, что не только свет, но также радиоволны, микроволновое излучение, инфракрасное излучение, ультрафиолетовое излучение, гамма-лучи – все являются электромагнитными волнами с разными длинами волн и частотой.
Электромагнитный спектр
См. Цвет (света).
Электромагнитный флюид, электромагнитное поле
Electromagnetic fluid/electromagnetic field
Поскольку электрическое и магнитное поля оказывают большое влияние друг на друга, удобно и справедливо рассматривать их как единое целое. Электромагнитный флюид – это просто флюид, двумя компонентами которого являются электрический и магнитный флюиды. Электромагнитное поле в любой точке равно среднему значению флюида в этой точке.
Электрон
Electron
Электроны – одна из составляющих частей обычного вещества. Впервые явным образом их наблюдал Дж. Томсон в 1897 г.
В Главной теории электроны – элементарные частицы, и их определяют через уравнения, которым они удовлетворяют.
В обычном веществе электроны несут весь отрицательный электрический заряд. Хотя они дают совсем небольшой вклад в массу обычного вещества, электроны играют преобладающую роль в химии и структуре материалов. Контролируемое управление электронами – другими словами, электроника, в широком понимании этого слова – это основа большой части современной технологической цивилизации.
Электронный флюид
Electron fluid
Электронный флюид – это заполняющий мировое пространство активный квантовый флюид или среда. Согласно квантовой теории, используемой в нашей Главной теории для описания мира, электроны и их античастицы – антиэлектроны, или позитроны – являются возмущениями электронного флюида. Они похожи в таком описании на волны на воде, которые в случае отсутствия препятствий могут сохраняться и передвигаться (или, как мы иногда говорим, «распространяться») долгое время и на большие расстояния.
Существуют похожие флюиды, связанные с каждым из видов элементарных частиц. (В физической литературе они часто называются квантовыми полями.) Эти заполняющие пространство флюиды сосуществуют – присутствие одного не исключает присутствие любого другого. Динамические уравнения Главной теории описывают, как они влияют друг на друга.
Как и многие идеи, которые мы используем сейчас для описания вещества, наше современное понимание электронов основано на понятиях, впервые появившихся в процессе изучения электромагнетизма и света. Электронный флюид очень похож на электромагнитный флюид, и сейчас мы рассматриваем электроны как наименьшие возмущения в электронном флюиде. Они являются его квантами, так же как фотоны для электромагнитного флюида.
Элементарная частица
Elementary particle
Мы называем частицу элементарной, если она подчиняется простым уравнениям. Согласно Главной теории, кварки, лептоны, фотоны, виконы, цветные глюоны, гравитоны и частица Хиггса – элементарные частицы.
Когда-то мы считали (или скорее надеялись), что протоны и нейтроны являются элементарными частицами, но дальнейшие исследования показали, что они не подчиняются простым уравнениям. Сходным образом атомы и молекулы также не являются элементарными частицами. Во всех этих случаях мы понимаем теперь, что эти объекты – протоны, нейтроны, атомы и молекулы – сложные структуры, состоящие из более простых частей. На самом деле они состоят из нескольких элементарных частиц Главной теории (а именно из u- и d-кварков, цветных глюонов, электронов и фотонов).
Эллипс
Ellipse
Эллипс – это плоская геометрическая фигура, похожая на вытянутый круг. Эллипсы обычно определяются следующим образом. Выберем пару точек А и B и расстояние d, большее, чем расстояние между A и B. Тогда набор всех точек P, таких, что сумма расстояний от A до P и от B до P равна d, является эллипсом. Точки A и B, которые сами по себе не принадлежат эллипсу, называются его фокальными точками, или фокусами.
Окружность является частным случаем эллипса, который возникает, когда A и B совпадают. Когда d много больше расстояния между A и B, эллипс становится почти окружностью. Когда d уменьшается и становится совсем немного больше расстояния от A до B, эллипс превращается в овал, плотно прилегающий к отрезку, соединяющему A и B; в предельном случае, когда d становится равно расстоянию между A и B, эллипс вырождается в этот отрезок.
Эллипс можно определить несколькими другими очень непохожими, но математически эквивалентными способами. Один из них, мой любимый, пожалуй, проще всего представить: нарисуйте круг на резиновом листе, а затем равномерно растяните лист в одном выбранном направлении. Тогда круг превратится в эллипс; все эллипсы можно получить таким способом.
Эллипсы были удивительно глубоко изучены древнегреческими геометрами просто потому, что казались им красивыми. Много веков спустя Кеплер путем внимательного изучения астрономических наблюдений Тихо Браге открыл, что орбиты планет вокруг Солнца образуют эллипсы с Солнцем в одном из фокусов. Хотя Кеплер сначала с огорчением отказался от «идеальных» орбит в форме окружностей, в ретроспективе это воплощение греческой геометрии кажется практически чудесным случаем, когда Идеальное становится Реальным.
Законы Кеплера о движении планет навели Ньютона на его теории механики и гравитации. В рамках работ Ньютона мы обнаруживаем, что планеты вращаются вокруг Солнца только по приближенно эллиптическим орбитам, так как они искажаются гравитационным влиянием других планет. Основная красота в данном случае заключается скорее в самих динамических законах, чем в их решениях. Чтобы узнать об этом больше, см. главу «Ньютон III».
Энергия, кинетическая энергия, энергия массы[123], энергия движения, потенциальная энергия и энергия поля
Energy/kinetic energy/mass energy/energy of motion/potential energy/field energy
Энергия наряду с импульсом и моментом импульса является одной из выдающихся сохраняющихся величин классической физики. Каждая из них также развилась в основополагающий столп современной физики.
В практических обсуждениях энергии вводится множество категорий, таких как энергия ветра, химическая энергия, тепловая энергия и другие, которые возникают в результате «заворачивания» фундаментальных форм энергии в разные обертки. Но даже если говорить об энергии в фундаментальных терминах, она имеет несколько форм. Здесь мы будем рассматривать энергию с фундаментальной точки зрения.
Полная энергия, которая является сохраняющейся величиной, равна сумме нескольких слагаемых: кинетической энергии, энергии массы, потенциальной энергии и энергии поля. Эти различные слагаемые относятся к сторонам реальности, которые, на первый взгляд, кажутся совершенно разными. Прикладная сила понятия энергии в немалой части как раз является результатом его способности описывать и связывать несколько различных аспектов реальности.
Кинетическая энергия исторически была первой формой энергии, о которой заговорили и значимость которой проще всего понять интуитивно. Качественно кинетическая энергия – это движение. Когда мы конструируем машины, мы часто хотим, чтобы что-то двигалось. Поскольку движущиеся объекты обладают кинетической энергией, часто основной целью энергетики является преобразование других форм энергии в кинетическую энергию.
Количественно, в механике Ньютона, кинетическая энергия частицы равна половине массы, умноженной на квадрат модуля скорости. В эйнштейновской модификации механики, чтобы удовлетворить специальной теории относительности, энергия движения становится связана с другой формой энергии – энергией массы, к которой мы сейчас обратимся.
В ньютоновской механике есть два отдельных закона сохранения: сохранение массы и сохранение энергии. Специальная теория относительности требует коренного пересмотра понятия массы. В рамках этого пересмотра необходимо отказаться от сохранения массы. Сохранение энергии остается в силе, но со значительно отличающимся определением того, что такое энергия. Хотя я никогда не видел, чтобы это преподносилось именно таким образом, логичность понятия энергии массы оказывается наиболее понятной, если рассматривать его как способ согласования нерелятивистского и релятивистского понятий энергии. Подробное объяснение дано в трех следующих абзацах.
Для импульса и момента импульса переход от релятивистского определения к ньютоновскому происходит плавно. Релятивистские выражения для этих величин становятся приближенно равными ньютоновским выражениям, когда скорости всех задействованных тел много меньше скорости света. Однако для энергии такой плавный переход не совсем очевиден. Он возможен, только если мы добавим новое слагаемое в привычное ньютоновское определение энергии. Этот новый вклад называется энергией массы.
Энергия массы тела равна его массе, умноженной на квадрат скорости света. Если обозначить, как это обычно делают, скорость света как c, соответствующая формула будет, пожалуй, самым известным уравнением в науке:
Emass = mc2.
Я добавил здесь нижний индекс mass, чтобы подчеркнуть, что это только одна из многих форм энергии. Полная энергия массы, когда у нас имеется несколько тел, просто равна сумме их энергий массы. Таким образом, полная энергия массы просто равна суммарной массе, умноженной на квадрат скорости света. Полная «скорректированная» ньютоновская энергия равна классической ньютоновской энергии – кинетической плюс потенциальной, – определение которой вы найдете в учебниках (а также ниже!), плюс энергия массы. Именно скорректированная ньютоновская энергия, а не классическая ньютоновская энергия, сама собой появляется в релятивистской механике.
При условии, что полная масса сохраняется, скорректированная и классическая ньютоновские энергии отличаются на константу (и обе они сохраняются). Однако скорректированная энергия работает в более общем случае. Она предусматривает некоторые случаи, такие как ядерные реакции, где сохранение массы не является хорошим приближением. В таких случаях энергия массы в начале процесса не равна энергии массы в конце. Полная энергия сохраняется, так что разность между этими энергиями массы должна появляться в других формах. Именно это имеют в виду, когда говорят о переходе массы в энергию или энергии в массу. Или, скорее, должны иметь в виду. Это понятие было мощным источником недопонимания и путаницы в научно-популярной литературе. Я надеюсь, что здесь помог разъяснить его.
Для точных вычислений и в приложениях, где есть несколько частиц, движущихся с околосветовыми скоростями, нужно использовать полные релятивистские формулы для энергии движения, и ее разделение на энергию массы и кинетическую энергию становится искусственным.
В интересах читателей, немного владеющих алгеброй, привожу эту формулу:
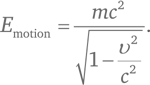
Когда модуль скорости много меньше скорости света, ? << c, это выражение становится приближенно равно сумме энергии массы mc? и ньютоновской кинетической энергии m?2/2, как мы описали выше. По мере того как модуль скорости приближается к скорости света, энергия движения растет неограниченно.
Потенциальная энергия, если качественно, это энергия положения, или расстояния. Например, потенциальная энергия камня вблизи поверхности Земли может быть запасена, если поднять камень, или потрачена, если его уронить. По мере того как камень падает после того, как его отпустили, его скорость, а значит, и его кинетическая энергия, растет. Следовательно, чтобы соблюсти сохранение энергии, его потенциальная энергия должна уменьшиться.
Понятие потенциальной энергии можно расширить, чтобы оно охватывало многие более общие случаи. Когда тела действуют с какими-то силами друг на друга, потенциальная энергия, связанная с их взаимодействием, является функцией расстояния между ними. Потенциальная энергия – энергия расстояния – это естественное понятие для теорий, основанных на дальнодействии, таких как теория гравитации Ньютона. Как и эти теории, она остается полезной во многих приложениях, где она предоставляет достаточно хорошее, удобное для пользователя приближение. Но в фундаментальной физике со времен революции, начатой Фарадеем и Максвеллом, передающие взаимодействие поля заменили дальнодействие. Энергия поля заменяет потенциальную энергию.
Энергия поля запасена по всему пространству, где есть не равные нулю поля. Например, плотность энергии поля, связанная с электрическим полем в точке пространства, пропорциональна квадрату модуля электрического поля в этой точке.
Возможность замены понятия потенциальной энергии, зависящей от расстояния, понятием энергии поля, определяемой локально, одновременно глубока и очень красива. Рассмотрим потенциальную энергию между положительно (электрически) заряженной и отрицательно заряженной частицами. По примерно таким же причинам, какие мы обсуждали в связи с камнем вблизи Земли, существует потенциальная энергия, связанная с расстоянием между этими частицами. В описании Фарадея – Максвелла то же самое количество энергии появляется совершенно иным образом. Оба наших заряда создают электрические поля, и полное электрическое поле равно сумме их вкладов. Плотность энергии, связанная с полным электрическим полем равна его квадрату, и значит, содержит не только квадраты каждого поля по отдельности, но также и перекрестный член, отражающий их одновременное присутствие. (Если эта идея вам не знакома, давайте на мгновение вернемся назад. Квадрат числа (1 + 1) = 2, т. е. 2 ? 2 = 4, не равен удвоенному квадрату единицы, т. е. двум. Есть еще один вклад, или перекрестный член, когда два независимых вклада в сумму встречаются в ее квадрате. В более общей алгебраической записи мы имеем (a + b)? = a? + b? + 2ab с перекрестным членом 2ab.) Перекрестные члены, которые появляются в полной плотности энергии поля, будут зависеть от относительной геометрии двух полей, из которых это поле состоит, которая в свою очередь зависит от относительного расстояния между частицами. Когда вы вычислите полную плотность энергии, включая вклады от всего пространства, чтобы получить полную энергию поля, вы обнаружите, что вклад этих перекрестных членов в точности совпадает с потенциальной энергией в старой теории и может ее заменить.
В этом примере энергия поля – это всего лишь другой (и более сложный!) способ прийти к тому же ответу, как и в случае потенциальной энергии. Но в более полном физическом представлении фундаментальные законы формулируются локально и естественным образом приводят к энергии поля. Потенциальная энергия – это приближенное производное понятие, полезное в некоторых задачах, но не подходящее для других.
Сохранение энергии и в конечном счете энергию саму по себе лучше всего можно понять с помощью обобщенной теоремы Нётер, которая связывает законы сохранения с симметрией. В таком подходе сохранение энергии свидетельствует о симметрии (инвариантности) физических законов относительно трансляции (сдвига) во времени – т. е. относительно преобразования, при котором все события сдвигаются вперед (или назад) на один и тот же интервал времени. Другими словами, сохранение энергии имеет место, когда законы не зависят от какого-либо заданного извне фиксированного времени.
В квантовом мире энергия приобретает дополнительные, очень тонкие и красивые свойства. Особенно примечательно соотношение Планка – Эйнштейна, которое связывает энергию фотонов и их цвет. В сочетании с идеями Бора эта связь позволяет нам расшифровать понятие спектра. Цвета спектрального света атома кодируют энергии его стационарных состояний, предоставляя видимую Музыку Сфер.
Энергия поля
См. Энергия.
Ядро
Nucleus
У каждого атома есть очень небольшая центральная часть, или ядро, которое содержит весь его положительный заряд и почти всю его массу. Как описано в главе «Квантовая красота III», исследование атомных ядер повлекло за собой открытие существования в Природе двух новых сил, сильного и слабого взаимодействий, и привело в течение XX в. к нашей изумительной Главной теории.
W-частица (W-бозон)
W particle
Массивная частица, которая играет одну из главных ролей в слабом взаимодействии. См. Слабое взаимодействие и Викон.
Z-частица (Z-бозон)
Z particle
Массивная частица, которая играет одну из главных ролей в слабом взаимодействии. См. Викон.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК