Исаак и маленькая луна

Предыдущая глава могла создать впечатление, будто я утверждаю, что Платон и Аристотель лишь повредили развитию науки. Я бы хотел скорректировать это впечатление. Аристотелевское исследование природы, например ботаники и зоологии, – это выдающиеся научные работы, основанные на тщательных наблюдениях за окружающим миром. Концептуальная ясность и внимание к разнообразию природы, впечатляющий интеллект и непредвзятость суждений великого философа обеспечили ему авторитет на долгие столетия. Первое известное нам систематическое изложение физики принадлежит Аристотелю, и это совсем неплохая физика.

Аристотель рассказывает о ней в книге, которая так и называется – «Физика». Заглавие этой книги не происходит от названия дисциплины – наоборот, дисциплина получила название по книге Аристотеля. Согласно Аристотелю, физика устроена следующим образом. В первую очередь, необходимо провести различие между небесами и Землей. В небесах всё состоит из кристаллической субстанции и вечно совершает круговые движения по огромным концентрическим окружностям, в центре которых находится сферическая Земля. На Земле необходимо различать вынужденные движения и естественные движения. Вынужденные движения вызываются усилием и прекращаются, когда прекращается усилие. Естественные движения направлены вертикально – вверх или вниз – и зависят от субстанции и ее расположения. Каждая субстанция имеет свое «естественное место» – так сказать, надлежащую высоту, на которую она всегда возвращается: земля внизу, вода немного выше, над ней воздух, а еще выше – огонь. Когда вы берете камень и позволяете ему упасть, он движется вниз, поскольку хочет вернуться к своему естественному уровню. Воздушные пузыри в воде, огонь в воздухе и взлетающие детские воздушные шарики – все они ищут свое естественное место.

Не надо смеяться над этой теорией или отбрасывать ее, поскольку она вполне физична. Это хорошее и корректное описание движения погруженных в жидкость тел, подвергающихся воздействию гравитации и трения, то есть реальных вещей, с которыми мы повседневно сталкиваемся в своей жизни. Это не ошибочная физика, как часто говорят. Это – приближение[33].

Физика Ньютона тоже является приближением к общей теории относительности. И вероятно, всё, что мы знаем сегодня, в свою очередь, является приближением к чему-то, чего мы еще не знаем. Конечно, физика Аристотеля довольно груба, она не имеет количественной формы (на ее основе нельзя делать расчеты), но она последовательна и рациональна и позволяет делать корректные качественные предсказания. Не зря она в течение столетий оставалась лучшей доступной моделью для понимания движения[34].

Платон, возможно, еще важнее для будущего развития науки.

Именно Платон понял всё значение догадок Пифагора и пифагорейцев: ключом к тому, чтобы пойти дальше Милетской школы, является математика.

Пифагор родился на Самосе, маленьком острове неподалеку от Милета. Его первые биографы Ямвлих и Порфирий рассказывают, что юный Пифагор был учеником престарелого Анаксимандра. Все началось в Милете. Пифагор много путешествовал, вероятно, по Египту и, возможно, даже побывал в Вавилоне, прежде чем осесть на юге Италии в Кротоне, где он основал свою религиозно-политико-научную секту, которая играла важную роль в политике маленького городка, но, помимо этого, оставила всему миру наследие огромной ценности – открытие теоретической полезности математики. Пифагору приписывают утверждение: «Число правит формами и идеями»[35].

Платон избавил пифагореизм от его обременительного и бесполезного мистического багажа. Он воспринял и очистил его полезный посыл: математика – это язык, лучше всего приспособленный для понимания и описания мира. Эффект от этой догадки был колоссальным; она стала одной из причин успеха западной науки. Согласно традиции, на двери своей школы Платон вырезал фразу: «Да не войдет сюда не знающий геометрии». Под влиянием этого убеждения Платон поднял важнейший вопрос, из которого после долгих окольных блужданий возникла современная наука. Он спрашивал у своих учеников, изучавших математику: могут ли они найти математические законы, которым следуют планеты, видимые на небосводе? Венеру, Марс и Юпитер легко увидеть на ночном небе. Их движения выглядят до некоторой степени беспорядочными: относительно звезд они перемещаются то в одну, то в другую сторону. Можно ли найти математическое описание, позволяющие предсказывать их движения?

Попытки найти эти законы начинаются с Евдокса в платоновской школе и продолжаются на протяжении следующих столетий такими астрономами, как Аристарх и Гиппарх; они поднимают античную астрономию на высочайший научный уровень. О достижениях этой науки мы знаем из единственной книги, которая дошла до нас, – «Альмагеста» Птолемея. Птолемей был астрономом, жившим в I веке нашей эры в Александрии, входившей в состав Римской империи, где наука тогда уже переживала спад и двигалась к полному исчезновению на фоне масштабного коллапса эллинистического мира, задушенного христианизацией Империи.

Книга Птолемея – это важнейший научный труд. Строгая, точная, сложная, она представляет астрономию как математическую систему, способную предсказывать кажущиеся беспорядочными движения планет по небу с почти безупречной точностью, ограниченной лишь возможностями человеческого глаза. Эта книга – доказательство того, что догадка Пифагора была верна. Математика позволяет описывать мир и предсказывать его будущее: внешне случайные и беспорядочные движения планет можно точно предсказать, используя формулы Птолемея, в которых объединены столетия труда греческих астрономов, представленные в тщательно систематизированном виде. Даже сегодня, приложив небольшие усилия, можно открыть книгу Птолемея, изучить его выкладки и вычислить, например, положение, которое займет Марс на небе в будущем. Сегодня, через 2000 лет после того, как книга была написана. Осознание того, что эта магия действительно работает, лежит в основании современной науки, и в немалой степени мы обязаны этим Пифагору и Платону.

После заката античной науки никто во всем Средиземноморье не был способен понять труды Птолемея, как и многие другие важные научные работы, пережившие катастрофу, такие как «Начала» Евклида. В Индии, куда греческое учение попало благодаря активным торговым и культурным связям, эти книги изучались и были поняты.

Из Индии это знание вернулось на Запад благодаря просвещенным персидским и арабским ученым, которые смогли понять и сохранить его. Однако астрономия за тысячу с лишним лет так и не сделала сколько-нибудь существенного шага вперед. Примерно в то же время, когда Поджо Браччолини обнаружил рукопись Лукреция, вольный дух итальянского гуманизма и интерес к античным текстам воодушевили юного поляка, который прибыл на учебу в Италию, сперва в Болонью, затем в Падую.

Он подписывался на латинский манер: Николаус Коперникус. Молодой Коперник изучил «Альмагест» Птолемея и буквально влюбился в него. Он решил посвятить жизнь астрономии, следуя по стопам великого Птолемея.

Пришло время, и более тысячи лет спустя после Птолемея Коперник смог продвинуться на шаг дальше, чем поколения индийских, арабских и персидских астрономов. Он не просто изучал и применял птолемееву систему, внося в нее небольшие поправки, но радикально усовершенствовал ее, смело изменив самые ее основания. Вместо того чтобы описывать, как небесные тела обращаются вокруг Земли, Коперник публикует своего рода пересмотренную и исправленную версию птолемеевского «Альмагеста», согласно которой Солнце находится в центре, а Земля вместе с другими планетами обращается вокруг него.

На этом пути, как надеялся Коперник, вычисления станут работать еще лучше. На деле они не были точнее, чем у Птолемея; в конечном счете, они даже оказались хуже птолемеевских. Но, несмотря на это, идеи Коперника вызвали резонанс: в следующем поколении Иоганн Кеплер показал, что систему Коперника можно заставить работать лучше птолемеевской. Тщательнейшим образом анализируя новые, точные наблюдения, Кеплер показал, что несколько новых математических законов могут описывать движение планет вокруг Солнца с точностью, превосходящий ту, что была достигнута в древности. Итак, только в 1600 году человечество впервые смогло сделать что-то лучше, чем это делалось в Александрии более тысячи лет назад.

Пока на холодном севере[36] Кеплер рассчитывал движения небесных тел, в Италии Галилео Галилей закладывал основания новой науки. Энергичный итальянец, любящий поспорить, убедительный, высокообразованный, исключительно умный и изобретательный, Галилей получил присланный из Голландии только что изобретенный телескоп и сделал шаг, изменивший человеческую историю. Он направил его в небо.

Подобно Рою из «Бегущего по лезвию бритвы», он видит вещи, в которые мы, люди, не можем поверить: кольца вокруг Сатурна, горы на Луне, фазы Венеры, спутники, обращающиеся вокруг Юпитера… Каждое из этих явлений делает идеи Коперника всё более правдоподобными. Научные инструменты начинают открывать близорукому человечеству вид на мир, который намного обширнее и многообразнее того, что люди могли себе вообразить.

Однако величайшая заслуга Галилея состояла в том, что он сделал логический вывод из космической революции, начатой Коперником. Галилей был убежден в том, что Земля – это такая же планета, как и все остальные; исходя из того что движения в небесах следуют точным математическим законам, а Земля – тоже планета и, таким образом, является частью небес, он пришел к выводу, что должны существовать точные математические законы, управляющие движениями предметов на Земле.

Уверенный в рациональности природы и в пифагорейско-платоновском представлении о том, что природу можно понять посредством математики, Галилей решает изучить, как движутся предметы на Земле, когда они свободны, то есть когда они падают. Будучи убежден в том, что должен существовать соответствующий математический закон, он начинает его поиск методом проб и ошибок. Впервые в истории человечества он ставит эксперимент. Экспериментальная наука начинается с Галилея. Его эксперимент очень прост: он позволяет предметам падать, то есть дает им возможность следовать тому, что для Аристотеля было их естественным движением, и старается точно измерить скорость их падения.

Результат эксперимента был поистине эпохальным: оказалось, что предметы вовсе не падают всё время с постоянной скоростью, как все полагали раньше. Напротив, в начале падения их скорость постоянно увеличивается. Постоянством на этой стадии характеризуется не скорость падения, а его ускорение, иначе говоря темп, в котором возрастает скорость. И удивительным образом это ускорение оказывается одинаковым для всех предметов. Галилей выполняет первое грубое измерение этого ускорения и находит, что оно постоянно. Его значение составляет примерно 9,8 метра в секунду за секунду, то есть каждую секунду своего падения предмет увеличивает скорость на 9,8 метра в секунду. Запомните это число.

Это первый математический закон, открытый для земных предметов: закон падения тел[37]. До этого момента были открыты лишь математические законы движения планет. Математическое совершенство больше не ограничено небесами.

И все же величайший результат еще впереди, и получит его не кто иной, как Исаак Ньютон. Ньютон тщательно изучает результаты Галилея и Кеплера и, объединяя их, находит настоящий скрытый бриллиант. Мы можем проследить за его рассуждениями на примере «маленькой луны», как делает он сам в «Математических началах натуральной философии» – книге, в которой оформились основания современной науки.

Представьте себе, что Земля, пишет Ньютон, имеет много лун, подобно Юпитеру. Помимо настоящей Луны, вообразим другие спутники, и в частности маленькую луну, которая обращается вокруг Земли на минимальном расстоянии от нее, чуть выше горных пиков. С какой скоростью двигалась бы эта маленькая луна? Один из открытых Кеплером законов связывает радиус орбиты с периодом обращения, то есть с временем, которое уходит на один полный оборот[38]. Мы знаем радиус орбиты настоящей Луны (Гиппарх измерил его еще в древности) и ее период обращения (один месяц). Мы знаем радиус орбиты маленькой луны (радиус Земли измерен Эратосфеном в древности). Из простой пропорции можно вычислить орбитальный период маленькой луны. Получается полтора часа. Маленькая луна совершала бы один оборот вокруг Земли каждые 90 минут.

Далее, находящийся на орбите объект не движется прямолинейно: он постоянно изменяет направление, а изменение направления – это ускорение. Маленькая луна ускоряется в направлении центра Земли. Это ускорение нетрудно подсчитать[39]. Ньютон делает простые вычисления и в результате получает… 9,8 метра в секунду за секунду! То же самое ускорение, что и у Галилея в экспериментах с падающими телами на Земле.

Совпадение? Не может быть, заключает Ньютон. Если результат одинаков – ускорение вниз величиной 9,8 метра в секунду за секунду, – то и причина должна быть одна. А значит, сила, которая заставляет маленькую луну обращаться по своей орбите, должна быть той же, что заставляет предметы падать на земную поверхность.

Мы называем силу, заставляющую предметы падать, гравитацией. Ньютон понимает, что эта самая гравитация заставляет маленькую луну обращаться вокруг Земли. Без гравитации она улетела бы прочь по прямолинейной траектории. Но тогда и настоящая Луна тоже должна обращаться вокруг Земли из-за гравитации! И спутники Юпитера притягиваются Юпитером, и планеты, которые обращаются вокруг Солнца, притягиваются Солнцем! Без этого притяжения любое небесное тело двигалась бы прямолинейно. И тогда Вселенная – это огромное пространство, где тела притягиваются друг к другу определенными силами и существует универсальная сила гравитации: каждое тело притягивается ко всем другим телам.

Грандиозная картина обретает форму. Внезапно, спустя тысячелетие исчезает разделение между небесами и Землей: больше нет «естественного уровня» для вещей, как предполагал Аристотель, нет центра мира, предметы обретают свободу и больше не стремятся к своему естественному месту, но движутся прямолинейно и вечно.

Простой расчет с маленькой луной позволяет Ньютону вывести, как гравитация меняется с расстоянием, и определить ее силу[40], характеризуемую величиной, которую сегодня называют ньютоновской гравитационной постоянной и обозначают буквой G (от слова gravity). На Земле эта сила заставляет предметы падать, в небесах она удерживает планеты и спутники на своих орбитах. Но это одна и та же сила.

Это – крушение аристотелевской картины мира, которая доминировала в представлениях людей на протяжении Средних веков. Подумайте, например, о вселенной Данте: как и у Аристотеля, Земля – это шар в центре Вселенной, окруженный небесными сферами. Теперь это не так. Вселенная – это громадное, бесконечное пространство, усеянное звездами, без границ и без какого-либо центра. Материальные тела в ней движутся свободно и прямолинейно, если только сила, порожденная другими телами, не отклоняет их. Отсылки к античному атомизму хорошо видны у Ньютона, даже когда он использует общепринятые понятия:

Мне кажется вероятным, что Бог вначале дал материи форму твердых, массивных, непроницаемых, подвижных частиц таких размеров и фигур и с такими свойствами и пропорциями в отношении к пространству…[41]

Мир ньютоновской механики прост и представлен на рис. 2.1 и 2.2. Это – возрожденный мир Демокрита. Мир, состоящий из огромного однородного пространства, всегда и везде подобного самому себе, в котором частицы вечно движутся, взаимодействуя друг с другом, – и ничего больше. Мир, воспетый Леопарди:

…Сижу, смотрю —

И бесконечные за ней пространства,

Молчанья неземные, глубочайший

Покой объемлю мыслью…[42]

Рис. 2.1. Из чего состоит мир?

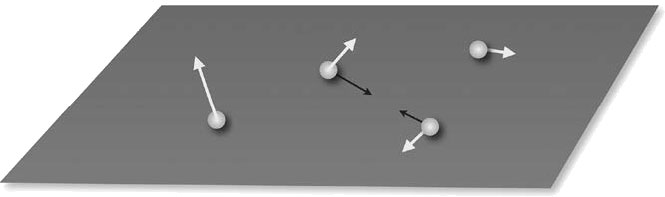
Рис. 2.2. Мир Ньютона: частицы, которые с течением времени движутся в пространстве, притягиваемые силами

Но эта картина намного сильнее демокритовского представления, поскольку это не просто мысленный образ, с помощью которого упорядочивается мир. Теперь эта картина объединена с математикой – наследием Пифагора и великой традицией математической физики александрийских астрономов. Мир Ньютона – это мир Демокрита, выраженный математическими средствами.

Ньютон без всяких колебаний признает, что новая наука очень многим обязана науке античной. Например, в первых же строках своего «Трактата о системе мира»[43] он указывает (корректно) на античное происхождение идеи, лежащей в основе коперниканской революции: «По мнению древних философов, в высочайших частях мира звезды закреплены и находятся в неподвижности, а Земля обращается вокруг Солнца»; однако он немного ошибается относительно достижений и открытий ученых прошлого и цитирует – иногда к месту, иногда нет – Филолая, Аристарха Самосского, Анаксимандра, Платона, Анаксагора, Демокрита и (!) «ученого Нума Помпилия, царя римлян».

Сила новой ньютоновской интеллектуальной парадигмы превзошла самые смелые ожидания. Вся технология XIX века и нашего современного мира основывается по большей части на ньютоновских формулах. Прошло три столетия, но мы по-прежнему сооружаем мосты, поезда и небоскребы, двигатели и гидравлические системы благодаря теориям, строящимся на ньютоновских уравнениях. Благодаря Ньютону мы знаем, как управлять самолетом, как делать метеорологические прогнозы, как предсказывать существование еще не обнаруженных планет и как отправлять космические аппараты на Марс… Современный мир не родился бы без маленькой луны Ньютона.

Новая картина мира, новый способ мышления, ставший источником вдохновения для просветителей – Вольтера и Канта, эффективный способ предсказания будущего: все это было и остается величайшим наследием ньютоновской революции.

Казалось, найден последний ключ к пониманию реальности: мир состоит только из великого, бесконечного пространства, где погруженные в поток времени частицы движутся и взаимодействуют друг с другом посредством сил. Действие этих сил можно описать с помощью точных уравнений, которые продемонстрировали свою невероятную эффективность. Вплоть до XIX века люди полагали, что Ньютон был не только одним из самых умных и дальновидных ученых, но также и самым удачливым, поскольку в мире существует лишь одна система фундаментальных законов и ему сказочно повезло стать ее первооткрывателем. Всё в мире казалось предельно ясным.

Но насколько эти представления соответствовали действительности?