Существует ли предел делимости?

Величайший физик второй половины XX века Ричард Фейнман писал в начале своего великолепного вводного курса лекций по физике:

Если бы в результате какой-то мировой катастрофы все накопленные научные знания оказались бы уничтоженными и к грядущим поколениям живых существ перешла бы только одна фраза, то какое утверждение, составленное из наименьшего количества слов, принесло бы наибольшую информацию? Я считаю, что это – атомная гипотеза (можете называть ее не гипотезой, а фактом, но это ничего не меняет): все тела состоят из атомов – маленьких телец, которые находятся в беспрерывном движении, притягиваются на небольшом расстоянии, но отталкиваются, если одно из них плотнее прижать к другому. В одной этой фразе, как вы убедитесь, содержится невероятное количество информации о мире, стоит лишь приложить к ней немного воображения и чуть соображения[15].

Не располагая знаниями современной физики, Демокрит тем не менее пришел к мысли, что всё состоит из неделимых частиц. Как ему это удалось?

Он использовал аргументы, основанные на наблюдении; например, он совершенно верно предполагал, что износ колеса и высыхание белья на веревке могут происходить из-за медленного улетучивания частиц соответственно дерева и воды. Кроме того, у него были аргументы философского плана. Сконцентрируемся на них, поскольку их сила простирается вплоть до квантовой гравитации.

Демокрит заметил, что вещество не может быть непрерывным целым, поскольку такое допущение приводит к противоречию. Мы знаем о рассуждениях Демокрита, поскольку их описывает Аристотель[16]. Представим, говорит Демокрит, что вещество бесконечно делимо, то есть его можно разделять на части до бесконечности. Что останется в результате?

Могут ли это быть крошечные частицы, имеющие протяженность? Нет, поскольку в этом случае такие частицы материи не были бы делимыми до бесконечности. Поэтому остаются только точки без протяженности. Но теперь попробуем составить кусок материи из таких точек: сложив вместе две точки без протяженности, вы не получите протяженную вещь, так же как и из трех точек и даже из четырех. На самом деле, сколько бы точек вы ни сложили вместе, вы никогда не получите протяженности, поскольку у точек ее нет. Поэтому материю нельзя представлять состоящей из точек, лишенных протяженности, потому что независимо от того, сколько точек мы объединим, мы никогда не сможем получить нечто, имеющее пространственную протяженность. Единственная возможность, заключает Демокрит, состоит в том, что любая часть вещества состоит из конечного числа дискретных неделимых порций, каждая из которых имеет конечные размеры, – атомов.

Это весьма тонкое рассуждение появилось еще до Демокрита. Его родина – область Чиленто в Южной Италии, где сейчас находится город Велия, а в V веке до нашей эры была процветающая греческая колония Элея. Здесь жил Парменид, философ, который буквально – в чем-то даже излишне – воспринял рационализм Милета и возникшую там идею о том, что разум способен показать нам, насколько вещи отличаются от того, чем они кажутся. Парменид пытался искать истину посредством одного только чистого разума, и этот путь привел его к утверждению, что всё видимое иллюзорно; это способствовало открытию нового направления мысли, которое со временем все более склонялось к метафизике, отдаляясь от того, что впоследствии стало естественными науками. Ученик Парменида Зенон, также родом из Элеи, стал автором изощренных аргументов в поддержку этого фундаменталистского рационализма, категорически отвергающего достоверность внешних проявлений. Среди этих рассуждений был набор парадоксов, известных как апории Зенона; они направлены на то, чтобы показать иллюзорность всего видимого, доказывая, что обыденное представление о движении абсурдно[17].

Самый знаменитый из парадоксов Зенона излагается в виде короткой басни. Черепаха вызвала Ахиллеса на состязание в беге с условием десятиметровой форы для себя. Сможет ли Ахиллес догнать черепаху? Зенон доказывает, что, согласно строгой логике, это ему никогда не удастся. Ведь прежде чем догнать черепаху, Ахиллес должен будет преодолеть 10 метров, и чтобы сделать это, ему понадобится некоторое время. За это время черепаха продвинется на несколько сантиметров. Чтобы преодолеть эти сантиметры, Ахиллесу потребуется еще немного времени, за которое черепаха продвинется еще чуть дальше, и так до бесконечности. Ахиллесу, таким образом, потребуется бесконечное число подобных шагов, чтобы догнать черепаху, а бесконечное число шагов, рассуждает Зенон, это бесконечное количество времени. Следовательно, согласно строгой логике, Ахиллесу потребуется бесконечное количество времени, чтобы догнать черепаху; иначе говоря, он никогда ее не догонит. Но поскольку мы видим, что проворный Ахиллес догоняет и обгоняет столько черепах, сколько захочет, мы приходим к заключению, что видимое нами иррационально и потому иллюзорно.

Честно говоря, всё это звучит не слишком убедительно. Но где же допущена ошибка? Один из возможных ответов состоит в том, что Зенон ошибался, полагая, что сложение бесконечного числа вещей приводит к бесконечной вещи. Представьте, что вы взяли кусок струны, разрезали его пополам, затем еще раз пополам и так до бесконечности. В конце вы получите бесконечное число крошечных кусочков струны; их сумма, однако, будет конечной, поскольку из них можно сложить лишь кусок струны исходного размера. Получается, что из бесконечного числа струн может получиться конечная струна; бесконечное число всё более коротких отрезков времени может складываться в конечное время, и герою, хотя и придется преодолеть бесконечное число постоянно уменьшающихся дистанций, удастся сделать это за конечное время и в итоге догнать черепаху.

Кажется, парадокс разрешен. Решение состоит в идее континуума: могут существовать сколь угодно малые отрезки времени, а их бесконечное число может складываться в конечный отрезок времени. Аристотель первым интуитивно понял эту возможность, которая в дальнейшем исследовалась древними и современными математиками[18].

Но является ли данное решение корректным для реального мира? Существуют ли на самом деле сколь угодно короткие отрезки струн? Действительно ли можно разделить отрезок струны на произвольное число частей? Существуют ли бесконечно малые отрезки времени? Это как раз те вопросы, с которыми сталкивается квантовая теория гравитации.

По преданию, Зенон встречался с Левкиппом и стал его учителем. Левкипп, таким образом, был знаком с парадоксами Зенона. Но он изобрел другой способ их разрешения. Левкипп предположил, что произвольно малых вещей не существует: у всего есть нижний предел делимости.

Вселенная зернистая, а не непрерывная. Как показано в описанном Аристотелем демокритовском рассуждении, из бесконечно малых точек было бы невозможно построить нечто протяженное. Так что протяженность струны должна образовываться конечным числом конечных объектов с конечными размерами. Струну нельзя разрезать сколько угодно раз; материя не является непрерывной, а состоит из отдельных «атомов» конечного размера.

Корректен этот абстрактный аргумент или нет, но, как мы знаем сегодня, он содержит большую долю истины. Материя действительно имеет атомарную структуру. Если я разделю каплю воды пополам, то получу две капли воды. Я могу вновь разделить каждую из этих капель пополам и так далее. Но я не могу продолжать делать это до бесконечности. В некоторый момент у меня останется лишь одна молекула, и я буду вынужден остановиться. Не существует капель воды, которые меньше одной молекулы воды.

Откуда мы знаем об этом сегодня? Подтверждения копились столетиями, большая часть из них пришла из химии. Химические соединения содержат сочетания нескольких элементов, взятых в пропорциях, задаваемых целыми числами. Химики стали думать о веществах как о состоящих из молекул, представляющих собой фиксированные сочетания атомов. Например, вода – H₂O – состоит из двух частей водорода и одной части кислорода.

Но эти наблюдения были лишь подсказками. Еще в начале прошлого века многие ученые и философы не считали реалистичной атомную гипотезу. Среди них был знаменитый физик и философ Эрнст Мах, чьи представления о пространстве могли сильно повлиять на Эйнштейна. В конце лекции Людвига Больцмана в Имперской академии наук в Вене Мах громко объявил: «Я не верю в существование атомов!» Это было в 1897 году. Многие, подобно Маху, воспринимали химические обозначения лишь как удобный способ краткого описания законов химических реакций, а не как свидетельство реального существования молекул воды, состоящих из двух атомов водорода и одного атома кислорода. Вы же не можете увидеть атомы, говорили они, их никогда нельзя будет увидеть. А раз так, спрашивали они, какого размера могут быть атомы? Демокрит так и не смог оценить размеры своих атомов…

Но это смог сделать кое-кто другой. Убедительного доказательства «атомной гипотезы» не было вплоть до 1905 года. Оно было найдено двадцатипятилетним молодым человеком с бунтарскими образом мысли, который изучал физику, но не смог найти работы как ученый и в конце концов нанялся в бернское патентное бюро. Я буду еще много рассказывать об этом молодом человеке и о трех статьях, которые он отправил в самый престижный физический журнал того времени – Annalen der Physik. Первая из этих статей содержала убедительное доказательство существования атомов и расчет их размеров, что решало проблему, поставленную Левкиппом и Демокритом за 23 века до этого.

Звали этого двадцатипятилетнего автора, конечно же, Альберт Эйнштейн.

Рис. 1.3. Альберт Эйнштейн

Как ему это удалось? Идея была на удивление простой. Ее мог бы найти любой, начиная с Демокрита, обладай он эйнштейновской проницательностью и необходимым знанием математики, позволяющим выполнить не самые простые вычисления. Вкратце суть идеи заключалась в следующем: если мы очень внимательно наблюдаем за мелкими объектами вроде пылинок или частиц пыльцы, которые окружены неподвижным воздухом или жидкостью, мы заметим, что они подрагивают, как бы пританцовывая. В результате они движутся случайными зигзагами и медленно перемещаются, постепенно удаляясь от стартовой точки. Такое перемещение частиц в жидкости называется броуновским движением в честь Роберта Брауна, биолога, который подробно описал его в XIX веке. Типичная траектория такой танцующей частицы изображена на рис. 1.4. Она выглядит так, будто крошечная частица получает случайные толчки с разных сторон. На самом деле она не «будто», а в действительности получает толчки. Она дрожит, поскольку сталкивается с отдельными молекулами воздуха, которые налетают на нее то справа, то слева.

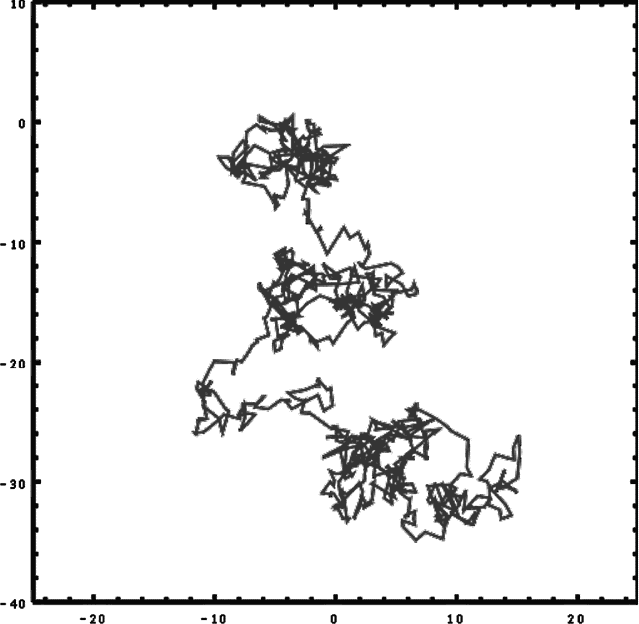
Рис. 1.4. Типичное броуновское движение

Ключевая мысль состоит в следующем. Число молекул в воздухе колоссально. В среднем частица получает столько же толчков слева, сколько и справа. Если бы молекулы воздуха были бесконечно малыми и бесконечно многочисленными, воздействия толчков справа и слева уравновешивались бы и в каждый момент взаимно компенсировали друг друга, в результате чего частица не двигалась бы. Но конечность размеров молекул – тот факт, что имеется лишь конечное, а не бесконечное их число – приводит к возникновению флуктуаций (это ключевое слово). Иначе говоря, столкновения никогда не уравновешиваются точно, они сбалансированы лишь в среднем. Представьте на мгновение, что молекул очень немного и они велики по размеру: очевидно, пылинка будет получать толчки лишь изредка, сначала справа, потом слева… Между столкновениями она будет значительно смещаться в ту или другую сторону, подобно мячу, по которому бьют мальчишки, играющие в футбол. С другой стороны, чем меньше молекулы, тем короче становятся интервалы между столкновениями и тем лучше уравновешиваются толчки с разных сторон. А смещения пылинки становятся менее значительными.

Оказывается, проделав кое-какие математические выкладки, можно по величине наблюдаемых движений частицы определить размеры молекул. Как я уже упоминал, Эйнштейн сделал это в возрасте 25 лет. Из наблюдений за движением частиц пыльцы в жидкости и по расстояниям, на которые им удавалось переместиться от своей исходной позиции, он определил размеры демокритовских атомов – элементарных кирпичиков, из которых состоит вещество. Спустя 2300 лет он нашел доказательство гениальной идеи Демокрита: материя зерниста.