Космос

Спустя два года после публикации своих уравнений Эйнштейн решает использовать их для описания пространства всей Вселенной, рассматриваемой в крупном масштабе. И здесь появляется еще одна из его замечательных идей.

Тысячи лет человек задавался вопросом: бесконечна Вселенная или у нее есть предел? Обе гипотезы влекут за собой серьезные проблемы. Бесконечность Вселенной, похоже, не выдерживает следующего рассуждения: если она бесконечна, значит, где-то должен существовать, например, читатель, абсолютно такой же, как вы, который читает эту же самую книгу (бесконечность поистине огромна, и не существует такого числа комбинаций атомов, чтобы заполнить ее объектами, всегда отличающимися друг от друга). Фактически должен существовать не один такой читатель, а бесконечное множество… Но если у Вселенной есть предел, то что же представляет собой ее граница? Как можно придать смысл границе, по другую сторону которой ничего нет? Еще в VI веке философ-пифагореец Архит Тарентский писал:

Окажись я на самом дальнем небе, на сфере неподвижных звезд, смог бы я протянуть за нее руку или палку? Нелепо думать, будто это должно быть невозможно; но если я могу это сделать, то существует нечто вовне, будь то материя или пространство. И так можно продолжать все дальше и дальше, постоянно задаваясь вопросом: всегда ли будет нечто, куда можно протянуть палку[61].

Кажется, что эти две абсурдные альтернативы – абсурд бесконечного пространства и абсурд Вселенной с фиксированной границей – не оставляет места для разумного выбора между ними.

Однако Эйнштейн находит третий путь: Вселенная может быть конечной и в то же время не иметь границы. Каким образом? Точно так же, как поверхность Земли не бесконечна, но не имеет границы, где бы она «кончалась». Подобное естественным образом происходит с искривленными вещами: поверхность Земли искривлена. И в общей теории относительности трехмерное пространство, конечно, может быть искривленным. Следовательно, наша Вселенная может быть конечной, но безграничной.

Если я буду все время идти по прямой линии на поверхности Земли, я не буду бесконечно удаляться, а в конце концов вернусь в ту точку, откуда вышел. Наша Вселенная может быть устроена подобным же образом: если я сяду на звездолет и буду все время лететь в одном направлении, я облечу Вселенную и в конце концов вернусь обратно на Землю. Трехмерное пространство такого типа – конечное, но безграничное – называется 3-сферой.

Для понимания геометрии 3-сферы обратимся к обычной сфере – поверхности мяча или Земли. Для изображения поверхности Земли на плоскости можно нарисовать два круга, как это обычно делают в случае карты мира (рис. 3.11).

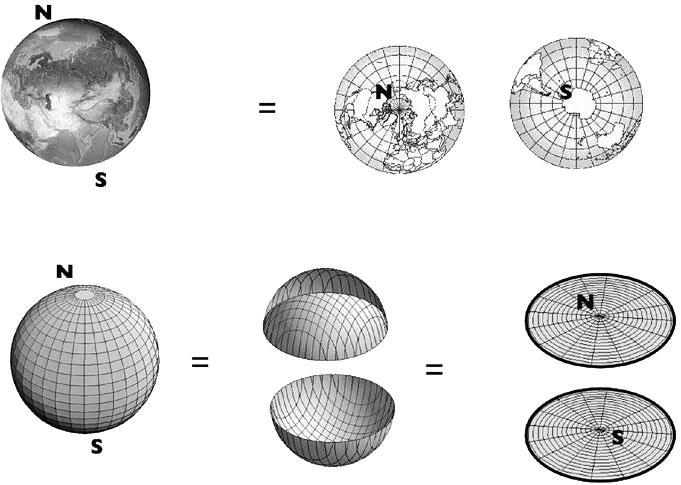
Рис. 3.11. Сферу можно изобразить в виде двух кругов, которые в действительности гладко соединяются друг с другом вдоль своих краев

Обратите внимание, что житель Южного полушария в некотором смысле окружен Северным полушарием, поскольку, в каком бы направлении ни покинул он свое полушарие, в результате он всегда попадет в другое. Но верно и обратное: каждое из полушарий окружает другое и окружено другим. Аналогичным образом можно представить себе и 3-сферу, но она рассматривается и в дополнительном измерении: два шара соединены друг с другом по всем своим границам (рис. 3.12).

Рис. 3.12. 3-сферу можно представить в виде двух шаров, соединенных друг с другом

Покидая один шар, мы вступаем в другой, точно так же как, покидая один круг карты мира, мы попадаем в другой. Каждый из шаров окружает другой и окружен им. Идея Эйнштейна состоит в том, что пространство может быть 3-сферой – иметь конечный объем (равный сумме объемов двух шаров), но не иметь границ[62]. В своей работе 1917 года Эйнштейн предложил 3-сферу в качестве решения проблемы границы Вселенной. С этой статьи начинается современная космология, изучение всей видимой Вселенной, рассматриваемой в самом крупном масштабе. Она порождает открытие расширения Вселенной, теорию Большого взрыва, проблему рождения Вселенной и еще много чего другого. Я подробнее расскажу обо всем этом в главе 8.

Есть еще одно замечание, которое я бы хотел сделать относительно эйнштейновской 3-сферы. Может показаться невероятным, но эта идея уже была предложена другим гением из совершенно иной культурной вселенной – великим итальянским поэтом Данте Алигьери. В «Рае», третьей части своей главной поэмы «Божественная комедия», Данте рисует величественный образ средневекового мира, уподобленный миру Аристотеля, со сферической Землей в центре, окруженной небесными сферами (рис. 3.13).

В сопровождении своей сияющей возлюбленной Беатриче, Данте в ходе фантастического мысленного путешествия поднимается по этим сферам до самой внешней сферы. Достигнув ее, он созерцает под собой мир с его вращающимися небесами и Землей далеко внизу в самом центре. Но затем он смотрит вверх – и что же он видит? Он видит светящуюся точку, окруженную огромными сферами ангелов, иными словами – другую колоссальную сферу, которая, по его словам, «окружает и в то же время окружена» сферой нашей Вселенной! Здесь в строках XXVII песни «Рая» он пишет: “Questa altre parte dell’Universo d’un cerchio lui comprende si come questo li altri”[63], а затем в XXX песни повторяет о последней точке: “parendo inchiuso da quell ch’elli inchiude”[64]. Точка света и сфера ангелов окружают Вселенную, и в тоже время они окружены Вселенной! Это точное описание 3-сферы![65]

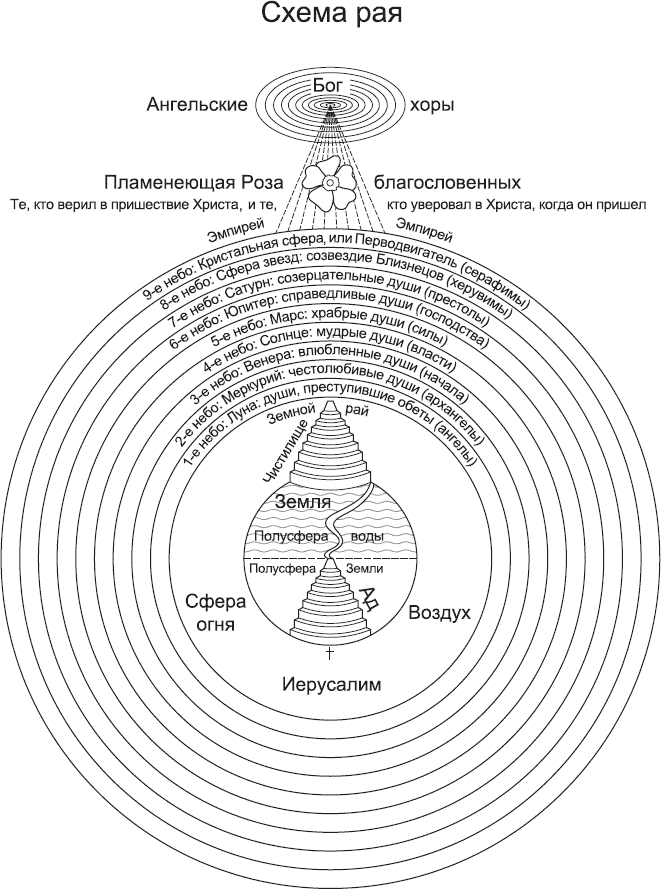
Рис. 3.13. Традиционное представление Вселенной Данте

Американский математик Марк Петерсон в 1979 году первым заметил, что «Рай» описывает Вселенную как 3-сферу. В целом исследователи творчества Данте не очень хорошо знакомы с 3-сферами. Однако любой современный физик или математик легко распознает 3-сферу в дантовском описании Вселенной.

Каким образом Данте могла прийти в голову идея, звучащая столь современно? Я думаю, это в первую очередь отражение глубочайшего интеллекта великого итальянского поэта. Именно его ум делает «Божественную комедию» такой восхитительной. Но также это связано с тем, что Данте писал задолго до того, как Ньютон убедил всех, что бесконечное пространство космоса имеет плоскую евклидову геометрию. Данте был свободен от ограничений, наложенных на нашу интуицию в результате ньютонианского обучения.

Научная культура Данте основывалась главным образом на поучениях его наставника Брунетто Латини, от которого до нас дошел небольшой очаровательный трактат «Li tresor», своего рода энциклопедия средневекового знания, написанная на дивной смеси старофранцузского и итальянского. В «Li tresor» Брунетто подробно объясняет, почему Земля является круглой.

Но он делает это странным для современного читателя способом – в категориях «внутренней», а не «внешней» геометрии. То есть он не пишет, что Земля похожа на апельсин, не говорит, как она выглядит, если смотреть на неё извне, а объясняет ее форму так: «Два рыцаря, которые достаточно далеко проскачут в противоположных направлениях, встретятся на противоположной стороне». И так: «Если бы не мешали моря, человек, начавший идти в одну сторону, вернулся бы в ту же точку Земли, откуда вышел». Иными словами, он использует внутреннюю, а не внешнюю точку зрения – с позиции того, кто идет по Земле, а не того, кто смотрит на нее со стороны. На первый взгляд, это может показаться бессмысленным, усложненным способом объяснения того, что Земля является шаром. Почему Брунетто просто не говорит, что Земля похожа на апельсин? Но с другой стороны, если мы скажем, что муравей ползет по апельсину, то в какой-то момент он окажется в перевернутом положении и должен будет удерживаться крошечными присосками на ногах, чтобы не упасть. Однако путешественник, идущий по Земле, никогда не оказывается в перевернутом положении и не нуждается в присосках на ногах. Так что описание Брунетто на самом деле не такое уж странное.

Теперь задумайтесь над этим. Некто узнал от своего учителя, что форма поверхности нашей планеты такова, что, двигаясь все время по прямой линии, мы возвращаемся в точку, откуда вышли. Вероятно, не так уж трудно сделать следующий очевидный вывод и осознать, что форма всей Вселенной такова, что, двигаясь все время по прямой линии, мы вернемся в ту же точку, из которой отправились: 3-сфера – это пространство, в котором «два крылатых рыцаря, способных лететь в противоположных направлениях, встретятся на противоположной стороне». Выражаясь более формально, описание геометрии Земли, предложенное Брунетто Латини в «Li tresor», дано в терминах внутренней геометрии (рассматриваемой изнутри), а не внешней (рассматриваемой снаружи), и это как раз такое описание, которое подходит для обобщения понятия сферы с двух измерений на три. Лучший способ описания 3-сферы – это не пытаться «увидеть ее снаружи», а описывать то, что происходит, когда вы движетесь внутри нее.

Метод, разработанный Гауссом для описания кривых поверхностей и обобщенный Риманом для описания искривления пространства в трех и более измерениях, в основе своей следует пути Брунетто Латини. Идея, можно сказать, состоит в том, чтобы описывать кривизну пространства не как «видимую со стороны», говоря, как оно искривляется во внешнем пространстве, а в тех понятиях, которые может воспринимать наблюдатель, находящийся внутри этого пространства и способный двигаться, всегда оставаясь в нем самом. Например, обычная сфера, как заметил Брунетто, – это такая поверхность, где все «прямые» линии возвращаются к исходной точке, пройдя одно и то же расстояние (длину экватора). 3-сфера – это трехмерное пространство, обладающее таким же свойством.

Эйнштейновское пространство-время искривлено не в том смысле, что оно изогнуто «во внешнем пространстве». Оно искривлено в том смысле, что его внутренняя геометрия, то есть сеть расстояний между его точками, которые можно измерять, оставаясь внутри него, не соответствует геометрии плоского пространства. Это пространство, где неверна теорема Пифагора точно так же, как она неверна на поверхности Земли[66].

Существует важный для понимания дальнейшего изложения способ убедиться в кривизне пространства изнутри него, не пытаясь взглянуть на него извне. Представьте себе, что вы находитесь на Северном полюсе и идете на юг, пока не достигнете экватора. При этом вы несете с собой стрелку, которая показывает вперед. Дойдя до экватора, вы поворачиваете налево, не меняя направление стрелки. Она по-прежнему показывает на юг, который теперь находится для вас справа. Пройдите немного на восток вдоль экватора, а затем поверните обратно на север, опять не меняя направление стрелки, которая теперь будет показывать назад. Когда вы вернетесь на Северный полюс, ваш маршрут замкнется, образовав петлю, но стрелка уже не будет показывать в том же направлении, что и при старте (рис. 3.14). Угол, на который повернулась стрелка при обходе петли, служит мерой кривизны.

Я еще вернусь к данному методу измерения кривизны с помощью петель в пространстве. Это будут петли, которые дали название теории петлевой квантовой гравитации.

Данте покидает Флоренцию в 1301 году, когда завершается изготовление мозаики купола Флорентийского баптистерия. Мозаика, изображавшая ад (работы Коппо ди Марковальдо, учителя Чимабуэ), вероятно, устрашавшая средневековых людей, часто упоминается как источник вдохновения Данте (рис. 3.15).

Я посетил баптистерий вскоре после начала работы над этой книгой в компании Эммануэлы Минней, которая убедила меня ее написать. Войдя в баптистерий и посмотрев вверх, я увидел сияющую точку света (свет исходит от фонаря на вершине купола), окруженную девятью ангельскими чинами с названиями, подписанными в следующем порядке: ангелы, архангелы, начала, власти, силы, господства, престолы, херувимы, серафимы. Это в точности соответствует структуре второй сферы рая. Вообразите себя муравьем на полу баптистерия, способным ползти в любую сторону; независимо от того, в каком направлении карабкаться по стене, вы достигнете потолка в одной и той же точке света, окруженной ангелами: точка света и ее ангелы одновременно окружают и окружены всем остальным убранством баптистерия (рис. 3.16).

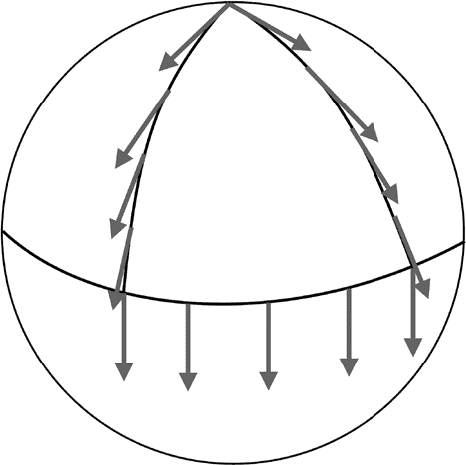
Рис. 3.14. Стрелка, сохраняющая параллельность самой себе при переносе вдоль замкнутого маршрута (петли), в искривленном пространстве возвращается к точке отправления повернутой

Рис. 3.15. Мозаика, изображающая ад, работы Коппо ди Марковальдо во Флорентийском баптистерии

Как и все жители Флоренции конца XIII века, Данте должен был быть преисполнен благоговейного трепета перед баптистерием, грандиозным архитектурным сооружением, возведенным его городом. Я думаю, что он мог вдохновляться баптистерием в своем видении космоса, причем не только «Адом» Коппо ди Марковальдо, но и всей архитектурой. «Рай» воспроизводит структуру баптистерия с замечательной точностью, включая девять кругов ангелов и точку света, только переносит ее из двух измерений в три. Описав сферическую Вселенную Аристотеля, Брунетто уже отмечает, что за ней лежит территория божественного, а средневековая иконография уже изображала рай как Бога, окруженного сферами ангелов. В конечном счете, Данте не более чем собрал все эти существовавшие фрагменты в согласованное архитектурное целое, следуя впечатляющей архитектуре баптистерия, и разрешил древнюю проблему границ Вселенной. Сделав это, Данте на шесть столетий опередил эйнштейновскую 3-сферу.

Рис. 3.16. Интерьер баптистерия

Я не знаю, сталкивался ли молодой Эйнштейн с «Раем» во время своих интеллектуальных странствий по Италии и оказало ли живое воображение итальянского поэта прямое влияние на его догадку о том, что Вселенная может быть одновременно конечной и безграничной. Но, независимо от возможности такого влияния, я считаю, что этот пример демонстрирует, как великая наука и великая поэзия способны давать нестандартный взгляд на вещи и даже приводить к одним и тем же догадкам. В нашей культуре наука и поэзия по какому-то недоразумению разделены, а ведь они обе открывают нам глаза на сложность и красоту мира.

Дантовская 3-сфера – это лишь образ из фантазии. Эйнштейновская 3-сфера имеет математическую форму и вытекает из уравнений теории. Влияние этих идей различно. Данте глубоко затрагивает источники наших эмоций. Эйнштейн открывает путь к нерешенным загадкам нашей Вселенной. Но каждый из них являет собой пример самого красивого и значительного полета человеческой мысли.

Но вернемся в 1917 год, когда Эйнштейн пытается включить представление о 3-сфере в свои уравнения. Здесь он сталкивается с проблемой. Он убежден, что Вселенная статична и неизменна, но его уравнения говорят, что это невозможно. Нетрудно понять почему. Все притягивается, а значит, для конечной Вселенной единственный способ избежать коллапса – расширяться. Точно так же, как единственный способ для футбольного мяча избежать падения на землю – получить удар, направленный вверх. Он либо летит вверх, либо падает вниз – он не может оставаться неподвижным, зависнув в воздухе.

Однако Эйнштейн не верит в то, что говорят ему собственные уравнения. Он даже допускает нелепую физическую ошибку (не понимает, что предложенное им решение является неустойчивым), лишь бы избежать принятия того, что предсказывает его теория: Вселенная либо сжимается, либо расширяется. Он модифицирует свои уравнения, пытаясь избежать вывода о расширении Вселенной. Именно с этой целью он добавляет в приведенное выше уравнение член ?g_ab. Но это новая ошибка: сам добавленный член корректен, но он не меняет того факта, что уравнение предсказывает расширение Вселенной. При всей смелости гению Эйнштейна не хватает храбрости поверить в собственные уравнения.

Спустя несколько лет Эйнштейн вынужден сдаться: верна его теория, а не его сомнения относительно нее. Астрономы обнаруживают, что все галактики действительно удаляются от нас – Вселенная расширяется, в точности как предсказывают уравнения. Около 14 миллиардов лет назад[67] Вселенная была сконцентрирована в одной безумно горячей точке. Из нее Вселенная расширилась в колоссальном космическом взрыве. И здесь слово «космический» употреблено не риторически, а в буквальном смысле – это взрыв самого космоса, Большой взрыв.

Сегодня мы знаем, что расширение Вселенной – реальность. Убедительное подтверждение сценария, предсказанного уравнениями Эйнштейна, было получено в 1964 году, когда двое американских радиоастрономов, Арно Пензиас и Роберт Уилсон, случайно открыли излучение, заполняющее Вселенную; это излучение оказалось остатком того самого невероятного жара, который царил в молодой Вселенной. И снова теория оказалась верна в своих самых удивительных предсказаниях.

С тех пор как мы обнаружили, что Земля круглая и вертится, как безумный волчок, мы поняли, что реальность не такая, какой она окажется: всякий раз, когда мы схватываем новый ее аспект, мы испытываем глубокое эмоциональное переживание. Еще одна пелена спадает с наших глаз. Но шаг, сделанный Эйнштейном, беспрецедентен: пространство-время – это поле; мир состоит из полей и частиц; пространство и время – это не что-то иное, отличное от всей остальной природы, а просто одно из полей среди других (рис. 3.17).

Рис. 3.17. Эйнштейновский мир: частицы и поля, которые движутся по другим полям

В 1953 году ученик начальной школы пишет Альберту Эйнштейну: «Наш класс изучает Вселенную. Меня очень интересует пространство. Я хотел бы поблагодарить Вас за все, что Вы сделали, чтобы мы могли его понять»[68].

Я полностью разделяю эти чувства.