Кванты 2: неопределенность

Мир – это последовательность зернистых квантовых событий. Они дискретны, зернисты и индивидуальны; это отдельные взаимодействия одной физической системы с другой. Электрон, квант поля или фотон не следуют по траекториям в пространстве, но появляются в определенном месте и в определенное время, чтобы столкнуться с другим объектом. Когда и где они появляются? Не существует способа узнать это наверняка. Квантовая механика кладет в основу мира фундаментальную неопределенность. Будущее принципиально непредсказуемо. Это второй фундаментальный урок квантовой механики.

Из-за этой неопределенности в мире, описываемом квантовой механикой, вещи постоянно подвержены случайным изменениям. Все переменные непрерывно флуктуируют, как если бы в мельчайших масштабах всё постоянно вибрировало. Мы не видим этих вездесущих флуктуаций лишь из-за малости их масштаба; в крупном масштабе, когда мы следим за макроскопическими телами, они ненаблюдаемы. Если смотреть на камень, он останется неподвижным. Но если бы мы могли видеть его атомы, то наблюдали бы, как они безостановочно вибрируют, постоянно смещаясь то туда, то сюда. Квантовая механика говорит нам, что чем глубже мы вглядываемся в детали мира, тем менее постоянными они оказываются. Мир не состоит из крошечных камешков. Это мир вибраций и непрерывных флуктуаций, кишащий быстротечными микрособытиями.

Античный атомизм предвидел и этот аспект современной физики – проявление на глубинном уровне законов вероятности. Демокрит (как и Ньютон) предполагает, что движение атомов строго детерминировано столкновениями. Но его последователь Эпикур исправляет этот детерминизм учителя и вводит в атомизм представление о неопределенности таким же способом, каким Гейзенберг ввел неопределенность в ньютоновский детерминизм. По Эпикуру, атомы могут иногда случайно отклоняться от своего курса. Лукреций поэтично описывает эти отклонения как происходящие «incerto tempore… incertisque loci» – в неопределенное время, в неопределенном месте[79]. Такая же случайность, такое же проявление вероятности на фундаментальном уровне представляют собой второе ключевое открытие, касающееся свойств нашего мира, которое выражает квантовая механика.

Итак, как вычислить вероятность того, что электрон, находившийся в определенной начальной позиции A, спустя заданное время вновь возникнет в той или иной финальной позиции B?

В 1950-х годах Ричард Фейнман, о котором я уже упоминал, нашел весьма интересный метод выполнения таких вычислений: рассмотрим все возможные траектории от A до B, то есть все мыслимые траектории, которым может следовать электрон, – прямые, искривленные, зигзагообразные… Каждая траектория определяет некоторое число. Вероятность получается путем суммирования всех этих чисел. Подробности вычислений несущественны, зато важен тот факт, что все траектории от A до B дают свой вклад, как будто электрон, чтобы попасть из A в B, проходит по всем возможным путям, или, иными словами, превращается в облако, чтобы затем загадочным образом собраться в точке B, где он вновь с чем-то сталкивается (рис. 4.7).

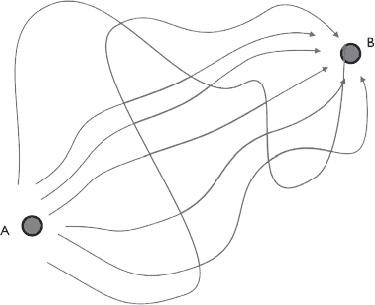
Рис. 4.7. При перемещении из точки A в точку B электрон ведет себя так, как будто проходит по всем возможным траекториям

Этот прием вычисления вероятности квантового события называется фейнмановским суммированием по путям[80], и мы увидим, что он играет важную роль в квантовой гравитации.