Пространственно-временное суши

Как эти общие идеи применяются к квантовой гравитации? Как описывать изменения без использования идеи пространства как контейнера и времени, вдоль которого скользит мир?

Рассмотрим процесс, например, столкновения двух бильярдных шаров на столе, обтянутом зеленым сукном. Пусть красным шаром бьют по желтому; он приближается, ударяется, и два шара разлетаются в разных направлениях. Этот процесс, как и все процессы, происходит в конечной области пространства (скажем, на столе шириной около двух метров) и длится конечное время (допустим, три секунды). Чтобы обсуждать этот процесс в контексте квантовой гравитации, необходимо включить пространство и время в сам этот процесс (рис. 7.1).

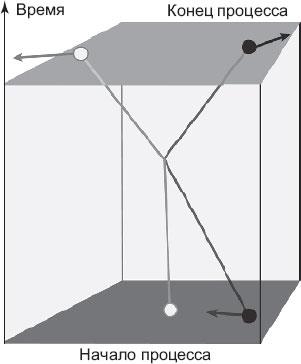
Рис. 7.1. Область пространства, в которой черный шар ударяет покоящийся белый шар, заставляя его двигаться, и отскакивает. Коробка – это область пространства-времени. Внутри нее нарисованы траектории шаров

Иными словами, мы должны описывать не только два шара, но также все, что находится вокруг них: стол и любые другие материальные объекты, а также пространство, в которое они погружены в течение времени, которое прошло между начальным ударом и концом процесса. Пространство и время – это гравитационное поле, эйнштейновский «моллюск»: мы также включаем в процесс гравитационное поле, то есть кусок этого моллюска. Все погружено внутрь этого огромного эйнштейновского моллюска. Теперь представьте, что вы отрезаете от него небольшой, конечный кусочек наподобие суши, который включает столкновение и то, что его окружает.

В результате мы получаем пространственно-временную коробку (как на рис. 7.1) – конечную порцию пространства-времени объемом несколько кубометров в пространстве и несколько секунд во времени. Этот процесс не происходит во времени. Эта коробка не находится в пространстве-времени, она включает в себя пространство-время. Это не процесс во времени – в том же смысле, в каком зерна пространства не находятся в пространстве. Течение времени – это лишь мера самого процесса, так же как кванты гравитации не находятся в пространстве, а сами представляют собой пространство.

Ключ к пониманию того, как работает квантовая гравитация, лежит в рассмотрении не только физического процесса, заданного двумя шарами, но и целостного процесса, заданного всей коробкой, со всем, что в ней содержится, включая гравитационное поле.

Теперь вернемся к первоначальный догадке Гейзенберга: квантовая механика говорит нам не о том, что происходит во время протекания процесса, но о вероятности, которая связывает различные начальные и конечные состояния этого процесса. В нашем случае начальные и конечные состояния задаются всем, что происходит на границе пространственно-временной коробки.

Уравнения петлевой квантовой гравитации дают нам вероятность, связанную с заданной возможной границей коробки, – вероятность того, что шары покинут коробку в той или иной конкретной конфигурации, если они вошли в нее в определенной начальной конфигурации.

Как вычисляется эта вероятность? Вспомним фейнмановскую сумму по путям, которую я описывал, когда рассказывал о квантовой механике. Вероятности в квантовой гравитации вычисляются таким же способом – путем рассмотрения всех возможных «траекторий», имеющих те же граничные условия. Поскольку мы включаем в рассмотрение динамику пространства-времени, это означает рассмотрение всех возможных пространств-времён, имеющих такую же границу, как у нашей коробки.

Квантовая механика предполагает, что между начальной границей, через которую два шара входят в коробку, и конечной границей, где они выходят, нет ни определенного пространства-времени, ни определенных траекторий шаров. Имеется только квантовое «облако», в котором сосуществуют все возможные пространства-времена и все возможные траектории. Вероятность увидеть шары выходящими одним или другим способом можно рассчитать, суммируя по всем возможным пространствам-временам.