Квантовая механика
XX век начался 1900 годом, в котором Макс Планк предложил модель, количественно описывающую спектр излучения черного тела. На рис. 6.1 изображен ее частный случай, описывающий излучение Солнца (я знаю, что Солнце желтое, тем не менее оно является черным телом по определению, так как не отражает свет). Эта модель основывалась на гипотезе, что свет не непрерывен, но состоит из порций энергии, которые Планк назвал квантами. Эти кванты несут в себе количество энергии, пропорциональное частоте излучения f. Коэффициент ?, теперь называемый постоянной Планка, ученый вычислил, согласовав его значение со спектральными данными. Вспомните, что частота света относится к длине его волны ? как ? = с/f, где с — это скорость света.
Закон сохранения энергии позволяет избежать ультрафиолетовой катастрофы классической волновой теории, о которой шла речь в главе 5. Коротковолновая часть спектра соответствует высокоэнергетическим квантам, и, поскольку у энергии тела есть предел, график спектральной плотности должен сужаться в области коротковолнового излучения. Кроме того, длина волны в области спектрального пика уменьшается при снижении температуры, поскольку, согласно статистической механике, о которой говорилось в главе 5, температура является мерой средней кинетической энергии тела. То есть чем горячее тело, тем меньше будет длина волны в области спектрального пика, а частота, в свою очередь, выше.
В том же самом удивительном 1905 году, когда Эйнштейн представил свою теорию относительности, он также развил идею Планка, предположив, что свет состоит из частиц, позднее названных фотонами, энергия которых пропорциональна частоте соответствующей электромагнитной волны. Это значит, что, если f — это частота волны, энергия каждого фотона этой волны Е = ?f, где ? — постоянная Планка. На основании этого предположения Эйнштейну удалось объяснить явление фотоэффекта. Электрический ток возникает, когда фотоны выбивают электроны из металла. Для этого им требуется минимальная энергия, вот почему существует пороговое минимальное значение частоты, при котором образуется электрический ток. В 1914 году американский физик Роберт Милликен экспериментально подтвердил предположение Эйнштейна.
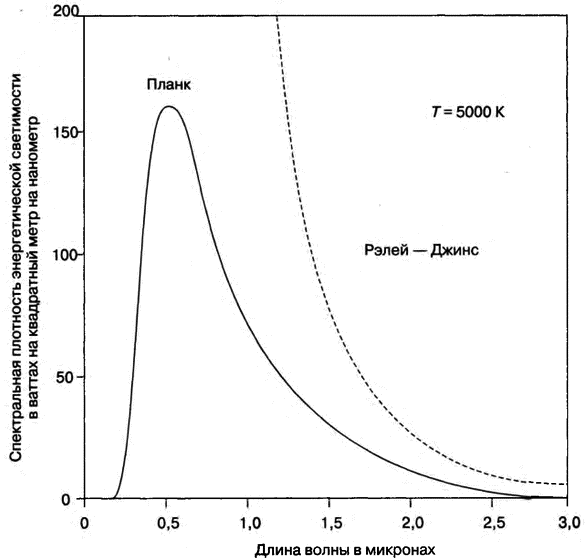
Рис. 6.1. Спектр интенсивности сферического черного тела с абсолютной температурой поверхности T = 5000 К как функция длины волны. Здесь изображена ультрафиолетовая катастрофа, предсказанная законом Рэлея — Джинса в рамках классической волновой теории, описанная в главе 5. Расчеты Планка соотносятся с экспериментальными данными. Шкала длин волн дана в микронах, или в миллионных долях метра, а шкала спектральной плотности — в киловаттах на квадратный метр на нанометр. Авторская иллюстрация
Эйнштейн доказал, что свет представляет собой не вибрации эфира или какой-то иной среды, но поток частиц, в точности как утверждал Ньютон в своей корпускулярной теории света. Но если свет состоит из частиц, то откуда берутся эффекты, подобные волновым, наблюдаемые в экспериментах интерференции и дифракции света?
Французский физик аристократического происхождения Луи де Бройль в 1924 году дал ответ на этот вопрос в своей докторской диссертации: все частицы имеют волновые свойства. Де Бройль заметил, что фотон с импульсом p имеет пропорциональную длину волны ? = ?/p. Он предположил, что это отношение верно для всех частиц, в частности для электронов. Эта величина была названа длиной волны де Бройля.
Гипотеза де Бройля подтвердилась в 1927 году, когда американские физики Клинтон Дэвиссон и Лестер Джермер наблюдали дифракцию пучка электронов, направленного на кристалл никеля.
Итак, не только фотоны, но и электроны, и вообще все частицы имеют волновые свойства. Это явление получило название корпускулярно-волнового дуализма. Однако здесь мы сталкиваемся еще с одним физическим эффектом, который большинство людей, включая физиков, понимают превратно. Часто можно услышать: «Объект является частицей или волной в зависимости от того, что вы измеряете». Это не так. Никому еще не удалось выявить волновые свойства у отдельно взятой частицы. Эффекты интерференции и дифракции наблюдаются только в потоках частиц, и ничего, кроме частиц, вы в них не обнаружите, даже если попытаетесь измерить длину волны этого излучения. Статистическое поведение этих групп частиц математически описывается уравнениями, которые иногда, но не всегда напоминают волновые.
Если вы проводите эксперимент по обнаружению интерференции или дифракции, в котором наблюдаете отдельные фотоны, то не заметите эти эффекты, пока не наберется большого числа наблюдений. К примеру, вы проводите двухщелевой эксперимент по определению интерференции в потоке фотонов, пропускающем один фотон в день.
Через год вы заметите, что начала формироваться интерференционная картина. Обратите внимание: не стоит говорить, что фотоны интерферируют друг с другом, как часто описывают этот эффект.
Если вы возразите мне, назвав один фотон в день лучом, то где вы проведете границу, у которой внезапно появляется этот луч? А один в час? Один в секунду? Один в наносекунду?
Позвольте мне прояснить этот момент. Будет неправильно говорить: «Этот фотон имеет частоту f» или «Этот электрон имеет длину волны ?». Правильные формулировки звучат так: «Этот фотон является частью группы фотонов, которые статистически можно описать как волну с частотой f» и «Этот электрон является частью группы электронов, которые статистически можно описать как волну с длиной волны ?».
В 1926 году австрийский физик Эрвин Шрёдингер разработал математическую теорию, названную волновой механикой, в которой он связал частицы с комплексным числом, называемым волновой функцией[9]. В том же году немецкий физик Макс Борн предложил интерпретацию, ставшую теперь общепринятой, согласно которой квадрат модуля волновой функции определяет вероятность обнаружения частицы в определенной точке пространства в пределах заданного объема и в определенный момент времени. Квантовая механика не позволяет предсказать поведение отдельной частицы в согласовании с приведенной ранее интерпретацией корпускулярно-волнового дуализма.
Чуть раньше, в 1925 году, немецкий физик Вернер Гейзенберг заложил основы науки, позже названной квантовой механикой, которая не работает с волнами, используя вместо этого матричную алгебру. Вначале шли споры о том, чья формулировка лучше. Шрёдингер доказал, что они математически эквивалентны. Формулировки Гейзенберга и Шрёдингера применяются только к нерелятивистским частицам, то есть тем, которые движутся на скоростях, значительно меньших, чем скорость света. Это значит, что с их помощью можно описать медленные электроны, но не фотоны.
В 1927 году британский физик Поль Дирак, чей гений сопоставим с эйнштейновским, сформулировал квантовую теорию фотонов. В следующем году он разработал релятивистскую теорию электронов, которая предсказывала существование антиматерии. В 1932 году американский физик Карл Андерсон сообщил, что ему удалось обнаружить в космическом излучении частицы, которые выглядели как электроны, но отклонялись в противоположном направлении в магнитном поле, а значит, имели положительный электрический заряд. Андерсон связал эти частицы с антиматерией Дирака и назвал антиэлектроны позитронами.
В 1930 году Дирак опубликовал основополагающую работу по квантовой механике — «Принципы квантовой механики»{103} В этой книге, выдержавшей с тех пор множество редакций и изданий, он избавился от понятия волновой функции, заменив волновую механику и матричную алгебру более мощным инструментом — линейной векторной алгеброй. Хотя большинство химиков и те из физиков, которые имеют дело с низкоэнергетическими процессами, могут обойтись менее замысловатой волновой механикой Шрёдингера, квантовая механика Дирака необходима для понимания поведения элементарных частиц и высокоэнергетических процессов вообще.
В то время как специальную теорию относительности благополучно привели в согласие с квантовой механикой, об общей теории относительности сказать того же нельзя. В частности — и это самое важное для нашей космологической истории — общая теория относительности неприменима к первым моментам существования нашей Вселенной, когда квантовые эффекты преобладали. Как мы вскоре увидим, это не удержало религиозных апологетов от использования аргументов общей теории относительности для доказательства божественного сотворения Вселенной.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК