Волнующая возможность

В 1987 г. Шин-Тун Яу и его студент Ганг Тиан, работающий сейчас в Массачусетском технологическом институте, сделали интересное математическое наблюдение. Используя хорошо известный математический приём, они обнаружили, что одни многообразия Калаби — Яу можно преобразовать в другие путём протыкания их поверхности и сшивания образовавшегося отверстия согласно строго определённой математической процедуре.^{75} Грубо говоря, они обнаружили, что внутри исходного пространства Калаби — Яу можно выделить двумерную сферу определённого вида (рис. 11.2).

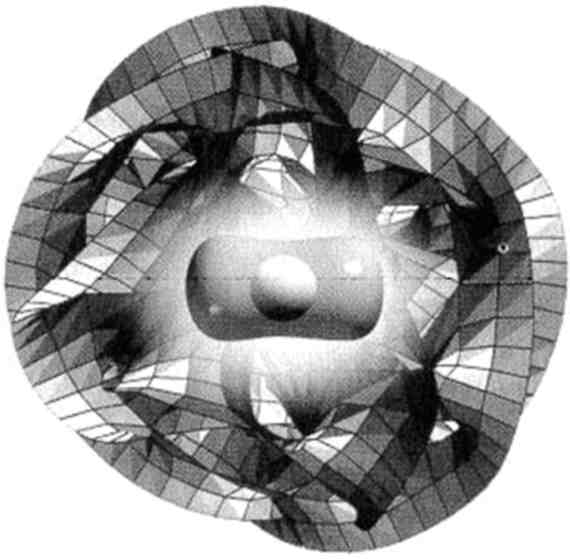
Рис. 11.2. В выделенной области внутри пространства Калаби — Яу находится сфера

(Двумерная сфера аналогична поверхности надувного мяча, который, как и все знакомые нам объекты, трёхмерен. Здесь, однако, мы говорим только о поверхности, не учитывая толщину материала, из которого сделан мяч, а также пространство внутри него. Точки на поверхности мяча определяются двумя числами, «широтой» и «долготой», аналогично тому, как определяются координаты на поверхности Земли. Вот почему поверхность мяча, как и поверхность упоминавшегося в предыдущих главах Садового шланга, является двумерной.) Далее они рассмотрели стягивание сферы в одну точку; этот процесс показан на рис. 11.3.

Рис. 11.3. Сфера внутри пространства Калаби — Яу сжимается в точку, приводя к перетяжке в ткани пространства. На этом и следующих рисунках для простоты показана лишь часть всего пространства Калаби — Яу

Как и все последующие рисунки этой главы, он упрощён с целью наглядности изображения наиболее важного «куска» пространства Калаби — Яу: но вы должны помнить, что такие преобразования происходят внутри несколько большего пространства Калаби — Яу, подобного изображённому на рис. 11.2. И, наконец, Тиан и Яу рассмотрели случай, когда в точке сжатия пространство Калаби — Яу слегка надрывается (рис. 11.4а), раскрывается и перестраивается в другую шарообразную фигуру (рис. 11.4б), которую затем снова можно раздуть до нормального размера (рис. 11.4в и 11.4 г).

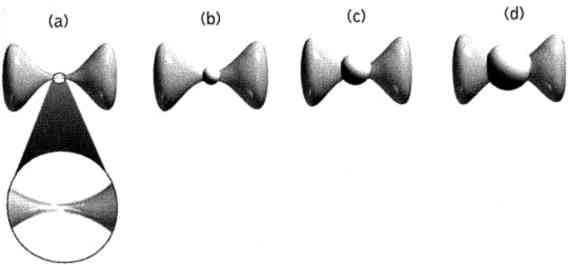
Рис. 11.4. При разрыве перетяжки пространства Калаби — Яу возникает сфера, которая сглаживает его поверхность. Исходная сфера рис. 11.3 оказывается «перестроенной»

Математики называют последовательность таких действий флоп-перестройкой[39]. Всё происходит так, как будто надувной мяч «выворачивается» наизнанку внутри другого пространства Калаби — Яу. Тиан, Яу и другие математики показали, что при определённых условиях новое многообразие Калаби — Яу (см. рис. 11.4 г), будет топологически отличным от исходного (рис. 11.3а). То есть, выражаясь привычным языком, не существует никакого способа деформировать исходное пространство Калаби — Яу, показанное на рис. 11.3а, в конечное пространство Калаби — Яу, показанное на рис. 11.4 г, не разрывая на некотором промежуточном этапе структуры пространства Калаби — Яу.

С точки зрения математики процедура Яу и Тиана очень интересна, так как позволяет получить новые пространства Калаби — Яу из уже известных. Но действительная сила процедуры проявляется в области физики, где в этой связи возникает волнующий вопрос: если забыть об абстрактном характере данной математической процедуры, может ли в природе иметь место изображённая на рис. 11.3а–11.4 г последовательность превращений? Может ли произойти так, что вопреки предсказаниям теории Эйнштейна структура пространства способна рваться и затем восстанавливаться подобно тому, как описано выше?