Гравитация и квантовая механика в теории струн

Единая схема, которую даёт теория струн, очень привлекательна. Но истинную неотразимость придаёт ей возможность избавиться от вражды между гравитационным взаимодействием и квантовой механикой. Вспомним, что проблема при объединении общей теории относительности и квантовой механики возникает, когда основное понятие первой из них — плавно искривлённая геометрическая структура пространства и времени — сталкивается с главной особенностью второй, что всё во Вселенной, включая структуру пространства и времени, испытывает квантовые флуктуации, интенсивность которых растёт при уменьшении масштаба исследований. На субпланковском масштабе расстояний квантовые флуктуации становятся столь сильными, что приводят к разрушению понятия гладкого искривлённого геометрического пространства, и это означает нарушение принципов общей теории относительности.

Теория струн смягчает неистовые квантовые флуктуации путём «размазывания» микроскопических характеристик пространства. На вопрос о том, что это значит в действительности и как это разрешает противоречие, есть два ответа: грубый и более точный. Мы поочерёдно рассмотрим каждый из них.

Грубый ответ

Хотя это звучит довольно наивно, один из способов, которым мы можем изучить структуру какого-либо объекта, состоит в том, чтобы бросать в него другие предметы и наблюдать за тем, как они отражаются от него. В качестве примера укажем, что мы способны видеть предметы потому, что наши глаза собирают, а наш мозг расшифровывает информацию, которую несут фотоны, отражающиеся от объектов, на которые мы смотрим. На этом же принципе основаны ускорители частиц: в них частицы материи, например, электроны и протоны, сталкиваются между собой и с другими объектами; затем специальные детекторы анализируют разлетающиеся осколки для получения информации, позволяющей определить структуру объектов, участвующих в столкновениях.

Общее правило при таких исследованиях состоит в том, что размер частиц, используемых для исследования, определяет нижний предел разрешающей способности измерительной установки. Чтобы лучше понять смысл этого важного утверждения, представим, что Слим и Джим решили приобщиться к культуре и записались в кружок по рисованию. По ходу занятий Джима начинают всё более раздражать растущие художественные способности Слима, и он вызывает его на необычное состязание. Он предлагает, чтобы каждый взял косточку от персика, закрепил её в тисках и изобразил наиболее точным образом. Необычность предложения Джима состоит в том, что ни ему, ни Слиму не разрешается смотреть на косточку. Вместо этого каждый из них может бросать в неё разные предметы (но не фотоны!), наблюдать за тем, как они отскакивают от косточки, и на этой основе определять размеры, форму и детали строения косточки (см. рис. 6.4). Тайком от Слима Джим заряжает его «стрелялку» крупными шариками (как на рис. 6.4а), а свою — пятимиллиметровыми пластиковыми пульками гораздо меньшего размера (как на рис. 6.4б). Оба заводят свои орудия, и состязание начинается.

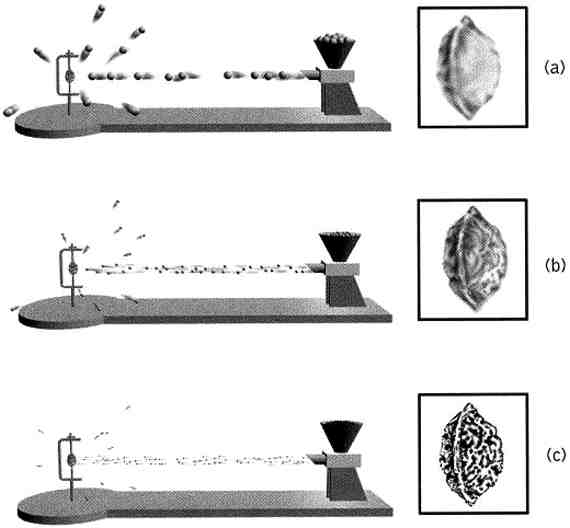
Рис. 6.4. Персиковая косточка закреплена в тисках. Для создания её изображения используются только наблюдения за тем, как отскакивают предметы — «зонды», — брошенные в неё. Используя зонды всё меньшего размера — шарики (а), пятимиллиметровые пульки (б), полумиллиметровые пульки (в), можно получать всё более детальное изображение

Лучшее, что удалось изобразить Слиму, показано на рис. 6.4а. Наблюдая за траекторией отскакивающих шариков, он смог установить, что размер косточки мал, и что она имеет твёрдую поверхность. Но это всё, что ему удалось узнать. Шарики были слишком велики, чтобы на них оказывали влияние более мелкие детали строения персиковой косточки. Когда Слим бросил взгляд на рисунок Джима (рис. 6.4б), он был поражён тем, что увидел. Однако быстрый взгляд на стрелялку Джима позволил ему понять, в чём дело: небольшие пульки, используемые Джимом, были достаточно малы, чтобы на угол, под которым они отражались, оказывали влияние некоторые крупные детали строения косточки. Таким образом, выстрелив в косточку большим количеством пятимиллиметровых пулек и наблюдая за их траекториями после отскока, Джим смог нарисовать более подробный рисунок. Чтобы не проиграть, Слим взял свою стрелялку, заполнил её снарядами ещё меньшего размера — полумиллиметровыми пульками, — которые так малы, что на характер их отражения будут оказывать влияние мельчайшие морщинки на поверхности косточки. Наблюдая за отскоком этих пулек, он смог нарисовать рисунок, который принёс ему победу (рис. 6.4в).

Урок, который можно извлечь из этого маленького состязания, ясен: размер частиц-зондов не может существенно превышать размер изучаемых физических особенностей; в противном случае разрешающая способность исследования окажется недостаточной для изучения интересующих нас структур.

Те же самые выводы относятся, конечно, и к случаю, когда мы захотим провести более глубокое исследование персиковой косточки, чтобы определить её структуру на атомном и субатомном уровне. Полумиллиметровые пульки не дадут никакой полезной информации по этому вопросу; они явно слишком велики, чтобы исследовать структуру на атомном уровне. Именно по этой причине в ускорителях в качестве зондов используются протоны или электроны: маленький размер этих частиц делает их гораздо более подходящими для этой цели. На субатомном уровне, где на смену классической логике приходят квантовые понятия, наиболее подходящей мерой разрешающей способности частиц является квантовая длина волны, которая определяет диапазон неопределённости местонахождения частиц. Этот факт является следствием приведённого в главе 4 обсуждения соотношения неопределённостей Гейзенберга. Там мы установили, что минимальная погрешность при использовании в качестве зонда точечных частиц (мы говорили о фотонных зондах, но сказанное применимо и ко всем другим частицам) примерно равна квантовой длине волны частицы, используемой в качестве зонда. Грубо говоря, разрешающая способность точечной частицы размазывается в результате действия квантовых флуктуаций подобно тому, как точность скальпеля хирурга уменьшается, когда его руки дрожат. Вспомним, однако, что в главе 4 мы также отметили один важный факт, состоящий в том, что квантовая длина волны частицы обратно пропорциональна моменту количества движения, который, грубо говоря, определяется её энергией. Таким образом, увеличивая энергию точечной частицы, можно делать её квантовую длину волны всё меньше и меньше, квантовое размазывание будет всё более уменьшаться и, следовательно, мы сможем использовать эту частицу для изучения всё более тонких структур. Интуитивно понятно, что частицы высокой энергии имеют бо?льшую проникающую способность и могут использоваться для изучения более мелких деталей строения.

В этом смысле становится очевидным различие между точечными частицами и нитями струн. Как в примере с пластиковыми пульками для изучения структуры поверхности персиковой косточки, присущая струне пространственная протяжённость не позволяет использовать её для исследования объектов, размер которых существенно меньше размера струны, в нашем случае — объектов, характерные размеры которых меньше планковской длины. Если перейти к более точным формулировкам, в 1988 г. Дэвид Гросс, работавший в то время в Принстонском университете, и его студент Пол Менде показали, что если учитывать квантовую механику, то непрерывное увеличение энергии струны не приводит к непрерывному увеличению её способности исследовать всё более тонкие структуры, в отличие от того, что имело бы место для точечной частицы. Они установили, что при увеличении энергии струны сначала её разрешающая способность растёт так же, как у точечной частицы высокой энергии. Однако, когда энергия струны превышает значение, необходимое для изучения структур в масштабе планковской длины, дополнительная энергия перестаёт вызывать увеличение разрешающей способности. Вместо этого дополнительная энергия приводит к увеличению размера струны, тем самым уменьшая её разрешающую способность. Типичный размер струны близок к планковской длине, но если накачать струну достаточной энергией, которую мы не можем даже представить, но которая могла существовать во время Большого взрыва, то можно было бы заставить струну вырасти до макроскопических размеров. Это был бы довольно топорный инструмент для изучения микромира! Всё выглядит так, как будто струна, в отличие от точечной частицы, имеет два источника размазывания: квантовые флуктуации, как для точечной частицы, а также собственные пространственные размеры. Увеличение энергии струны уменьшает размазывание, связанное с первым источником, но, в конечном счёте, увеличивает размазывание, обусловленное вторым. В результате, как бы вы ни старались, физические размеры струны не позволят вам использовать её на субпланковском масштабе расстояний.

Но ведь конфликт между общей теорией относительности и квантовой механикой возникает благодаря свойствам структуры пространства, проявляющимся в субпланковском масштабе расстояний. Если элементарные компоненты Вселенной непригодны для исследований на субпланковских масштабах расстояний, это значит, что ни они, ни какие-либо объекты, состоящие из таких компонентов, не могут испытывать влияния этих кажущихся гибельных квантовых флуктуаций на малых масштабах. Это похоже на то, что произойдёт, если мы проведём рукой по полированной гранитной поверхности. Хотя на микроскопическом уровне гранит является дискретным, зернистым и неровным, наши пальцы не смогут обнаружить эти микроскопические неровности, и поверхность покажется нам абсолютно гладкой. Наши толстые, длинные пальцы «смажут» микроскопическую дискретность. Подобно этому, поскольку струна имеет конечные пространственные размеры, существует нижний предел её разрешающей способности. Струна не способна обнаружить изменения на субпланковском масштабе расстояний. Подобно нашим пальцам на граните, струна смажет ультрамикроскопические флуктуации гравитационного поля. И хотя результирующие флуктуации по-прежнему остаются значительными, это смазывание сгладит их в степени, достаточной для преодоления несовместимости общей теории относительности и квантовой механики. В частности, теория струн ликвидирует обсуждавшиеся в предыдущей главе фатальные бесконечности, возникающие при попытке построить квантовую теорию гравитации на основе модели точечных частиц.

Существенное различие между аналогией с гранитом и нашей реальной проблемой структуры пространства состоит в том, что существуют способы обнаружить микроскопическую дискретность поверхности гранита. Для этого могут использоваться более точные зонды, чем наши пальцы. Электронный микроскоп способен обнаружить поверхностные структуры, размер которых составляет менее одной миллионной доли сантиметра; этого достаточно, чтобы увидеть многочисленные неровности на поверхности. В противоположность этому, в теории струн нет способа обнаружить «неровности» в структуре пространства на субпланковском уровне. Во Вселенной, управляемой законами теории струн, уже не является истинной обычная точка зрения, согласно которой мы можем без ограничения делить объекты на всё более и более мелкие части. Предел существует, он вступает в игру, когда мы сталкиваемся с разрушительной квантовой пеной, показанной на рис. 5.1. Следовательно, в определённом смысле, который станет яснее в последующих главах, можно утверждать, что бурные квантовые флуктуации на субпланковских расстояниях не существуют. Как выразился бы позитивист, объект или явление существует, только если мы можем — хотя бы в принципе — исследовать и измерить его. Поскольку предполагается, что струны являются наиболее фундаментальным объектом мироздания и имеют слишком большой размер, чтобы на них оказывали влияние флуктуации структуры пространства, происходящие на субпланковских расстояниях, эти флуктуации не могут быть измерены, и, следовательно, согласно теории струн они не существуют.

Ловкость рук?

Обсуждение, приведённое выше, может оставить у вас чувство неудовлетворённости. Вместо того чтобы показать, что теория струн укрощает субпланковские флуктуации структуры пространства, мы, похоже, использовали ненулевой размер струн для того, чтобы обойти всю проблему стороной. Решили ли мы вообще хоть что-нибудь? Решили. Следующие два соображения позволят нам лучше понять это.

Прежде всего вывод, который можно сделать из предыдущего обсуждения, состоит в том, что предполагаемые флуктуации структуры пространства в масштабе субпланковских расстояний связаны исключительно с формулировкой общей теории относительности и квантовой механики в рамках модели, основанной на точечных частицах. Это означает, что центральное противоречие современной теоретической физики в определённом смысле является проблемой, которую породили мы сами. Поскольку мы ранее предположили, что все частицы вещества и все частицы, передающие взаимодействие, должны быть точечными объектами, практически не имеющими пространственной протяжённости, мы были обязаны рассматривать свойства Вселенной на произвольно малых масштабах. И на самых малых расстояниях мы столкнулись с проблемой, выглядящей неразрешимой. Теория струн утверждает, что мы столкнулись с этой проблемой только потому, что не поняли истинных правил игры: новые правила гласят, что существует предел тому, насколько глубоко можно исследовать Вселенную, — предел, определяющий, до какого уровня наше обычное понятие расстояния может применяться к ультрамикроскопической структуре мироздания. Становится понятно, что фатальные флуктуации структуры пространства возникают в наших теориях из-за неосведомлённости об этих пределах: модель с точечными частицами далеко выходит за рамки физической реальности.

Видя кажущуюся простоту этого решения, позволяющего разрешить конфликт, возникающий между общей теорией относительности и квантовой механикой, вы можете удивиться, почему прошло столько времени, пока учёные не осознали, что точечная модель частиц всего лишь идеализация, и что в реальном мире элементарные частицы имеют некоторые конечные размеры. Это второй момент, на который мы хотели бы обратить внимание. Уже давно некоторые из величайших умов теоретической физики, такие как Паули, Гейзенберг, Дирак и Фейнман, предполагали, что компоненты природы в действительности могут быть не точками, а маленькими, колеблющимися «капельками» или «ядрышками». Однако они, как и другие учёные, столкнулись с тем, что очень трудно построить теорию, фундаментальные компоненты которой не являются точечными частицами, и которая, в то же время, совместима с основополагающими физическими принципами, такими, как сохранение квантово-механической вероятности (согласно которому физические объекты не могут внезапно исчезать из Вселенной без всякого следа) и невозможность передачи информации со скоростью, превышающей скорость света. Снова и снова их исследования с разных точек зрения показывали, что отказ от парадигмы точечных частиц приводит к несоблюдению одного из этих принципов или их обоих. Поэтому в течение долгого времени казалось невозможным построить разумную квантовую теорию, основанную на чём либо ином, кроме точечных частиц. За двадцать с лишним лет глубоких исследований выяснилась поистине впечатляющая особенность теории струн: при всей непривычности некоторых понятий теория струн обладает всеми свойствами, которые должна иметь каждая разумная физическая теория. И, более того, благодаря наличию мод колебаний, реализующих гравитон, теория струн представляет собой квантовую теорию, включающую гравитацию.