Как выглядят свёрнутые измерения?

Дополнительные пространственные измерения теории струн не могут быть свёрнуты произвольным образом: уравнения, следующие из теории струн, существенно ограничивает геометрическую форму, которую они могут принимать. В 1984 г. Филипп Канделас из университета штата Техас в г. Остине, Гари Горовиц и Эндрю Строминджер из университета штата Калифорния в г. Санта-Барбара, а также Эдвард Виттен показали, что этим условиям удовлетворяет один конкретный класс шестимерных геометрических объектов. Они носят название пространств Калаби — Яу (или многообразий Калаби — Яу[32]), в честь двух математиков, Эудженио Калаби из университета штата Пенсильвания и Шин-Туна Яу из Гарвардского университета, исследования которых в близкой области, выполненные ещё до появления теории струн, сыграли центральную роль в понимании этих пространств. Хотя математическое описание пространств Калаби — Яу является довольно сложным и изощрённым, мы можем получить представление о том, как они выглядят, взглянув на рисунок.^{45}

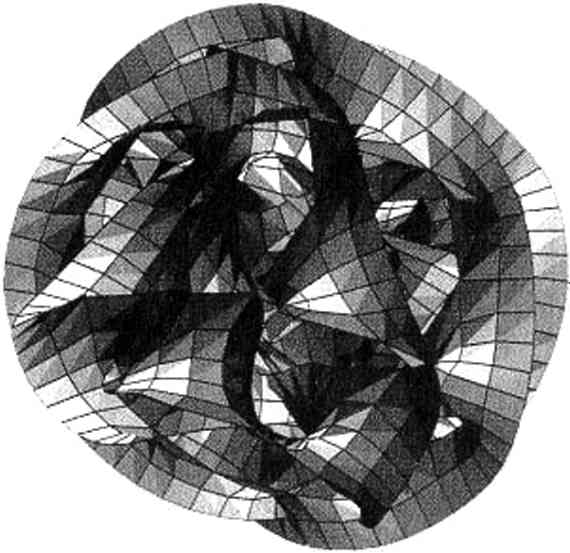
Рис. 8.9. Пример пространства Калаби — Яу

Пример пространства Калаби — Яу показан на рис. 8.9.^{46} Когда вы будете рассматривать этот рисунок, вы должны помнить, что ему присущи некоторые ограничения. Мы попытались представить шестимерное пространство на двумерном листе бумаги, что неизбежно привело к довольно существенным искажениям. Тем не менее, рисунок передаёт основные черты внешнего вида пространств Калаби — Яу.^{47} На рис. 8.9 иллюстрируется всего лишь один из многих десятков тысяч возможных видов пространств Калаби — Яу, которые удовлетворяют строгим требованиям к дополнительным измерениям, вытекающим из теории струн. Хотя принадлежность к клубу, в который входят десятки тысяч членов, нельзя считать эксклюзивной особенностью, вы можете сравнить это число с бесконечным числом форм, которые возможны с чисто математической точки зрения; в этом смысле пространства Калаби — Яу действительно являются достаточно редкими.

Чтобы получить общую картину, вы должны теперь мысленно заменить каждую из сфер, показанных на рис. 8.7 и представляющих два свёрнутых измерения, пространством Калаби — Яу. Иначе говоря, как показано на рис. 8.10, в каждой точке нашего привычного трёхмерного пространства согласно теории струн имеется шесть доселе неведомых измерений, тесно свёрнутых в одну из этих довольно причудливых форм.

Рис. 8.10. Согласно теории струн Вселенная имеет дополнительные измерения, свёрнутые в пространство Калаби — Яу

Эти измерения представляют собой неотъемлемую и вездесущую часть структуры пространства, они присутствуют повсюду. Например, если вы опишете рукой широкую дугу, ваша рука будет двигаться не только в трёх развёрнутых измерениях, но и в этих свёрнутых. Конечно, поскольку эти свёрнутые измерения столь малы, ваша рука в своём движении пересечёт их бесчисленное количество раз, снова и снова возвращаясь к исходной точке. Размеры этих измерений настолько малы, что в них не слишком много места для перемещения таких огромных объектов, как ваша рука, и все они «размазываются»: закончив движение руки, вы остаётесь в полном неведении о путешествии, которое она совершила сквозь свёрнутые измерения Калаби — Яу.

Это поразительная особенность теории струн. Но если у вас практичный ум, вы обязаны вернуться к обсуждению существенных и конкретных вопросов. Теперь, когда мы лучше понимаем, как выглядят дополнительные измерения, мы можем задать вопрос, какие физические свойства обязаны своим происхождением струнам, колеблющимся в этих измерениях, и как сравнить эти свойства с результатами экспериментальных наблюдений? В викторине под названием «теория струн» это вопрос на миллион долларов.