Точка зрения Фейнмана
Ричард Фейнман был одним из величайших физиков-теоретиков со времён Эйнштейна. Он полностью принял вероятностную интерпретацию квантовой механики, но после Второй мировой войны предложил новый взгляд на эту теорию. С позиций численных предсказаний точка зрения Фейнмана полностью согласуется с тем, что было известно ранее. Но её формулировка существенно отличается от общепринятой. Рассмотрим её в контексте экспериментов с электронами и двумя щелями.
Проблема с интерпретацией рис. 4.8 возникает потому, что в нашем представлении электрон проходит либо через левую щель, либо через правую, и поэтому мы рассчитываем увидеть комбинацию картин рис. 4.4 и 4.5, показанную на рис. 4.6. Электрону, проходящему через правую щель, должно быть всё равно, существует ли левая щель, и наоборот. Но каким-то образом он её чувствует. Получаемая интерференционная картина требует взаимодействия и сообщения между чем-то, чувствительным к обеим щелям, даже если электроны выстреливаются поодиночке. Шрёдингер, де Бройль и Борн объясняли этот феномен, приписывая каждому электрону волновую функцию. Подобно волнам на поверхности воды, показанным на рис. 4.7, волны функции плотности вероятности электрона «видят» обе щели и испытывают своего рода интерференцию при наложении. На тех участках, где вероятностная волна усиливается при наложении, подобно участкам значительного усиления колебаний на рис. 4.7, обнаружение электрона вероятно, а там, где вероятностная волна ослабляется при наложении, подобно местам с минимальной амплитудой или отсутствием колебаний на рис. 4.7, обнаружение электрона маловероятно или невероятно. Электроны сталкиваются с фосфоресцирующим экраном один за другим, распределённые в соответствии с функцией плотности вероятности и, в конечном итоге, образуют интерференционную картину, схожую с той, которая показана на рис. 4.8.
Фейнман выбрал другой подход. Он усомнился в основном классическом предположении, согласно которому каждый электрон проходит либо через левую щель, либо через правую. На первый взгляд это предположение настолько фундаментально, что сомневаться в нём нелепо. В конце концов, разве вы не можете заглянуть в область, расположенную между щелями и фосфоресцирующим экраном, и посмотреть, сквозь какую щель проходит каждый электрон? Да, вы можете. Но тем самым вы измените эксперимент. Чтобы увидеть электрон, вы должны сделать с ним что-нибудь — например, осветить его, т. е. столкнуть с ним фотон. В повседневных масштабах фотон действует как исчезающе малый зонд, который отскакивает от деревьев, картин и людей, не оказывая практически никакого влияния на движение этих сравнительно больших материальных тел. Но электрон — это ничтожно малая частица материи. Независимо от того, насколько осторожно вы будете определять щель, через которую он прошёл, отражающиеся от электрона фотоны неизбежно повлияют на его последующее движение. А это изменение движения изменит результат нашего эксперимента. Если ваше вмешательство будет достаточно сильным для того, чтобы вы смогли определить щель, через которую прошёл электрон, результат эксперимента изменится, и вместо картины, показанной на рис. 4.8, вы получите картину, подобную той, которая изображена на рис. 4.6! Квантовый мир гарантирует, что как только вы установили, через какую щель, правую или левую, прошёл каждый электрон, интерференция между этими двумя щелями исчезнет.
Таким образом, Фейнман укрепился в своих сомнениях: хотя повседневный опыт говорит о том, что электрон должен проходить через одну из двух щелей, к концу 1920-х гг. физики поняли, что любая попытка проверить это якобы фундаментальное свойство неизбежно приведёт к искажению результатов эксперимента.
Фейнман провозгласил, что каждый электрон, который проходит через преграду и попадает на фосфоресцирующий экран, проходит через обе щели. Это звучит дико, но не торопитесь возмущаться, вас ждут ещё более сумасшедшие заявления. Фейнман высказал утверждение, что на отрезке от источника до некоторой точки на фосфоресцирующем экране каждый отдельно взятый электрон на самом деле перемещается по всем возможным траекториям одновременно; некоторые из этих траекторий показаны на рис. 4.10.
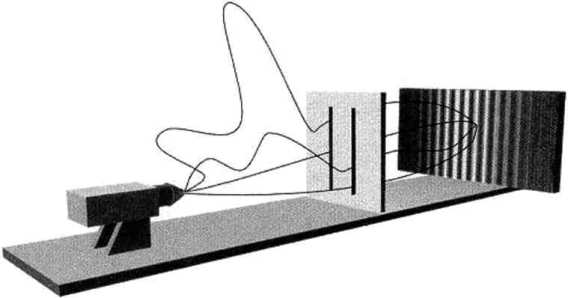
Рис. 4.10. Согласно формулировке квантовой механики, предложенной Фейнманом, частица, перемещающаяся из одной точки в другую, движется одновременно по всем возможным путям. Здесь показано несколько из бесконечного числа возможных траекторий для одного электрона, движущегося от источника к фосфоресцирующему экрану. Обратите внимание, что этот один электрон на самом деле проходит через обе щели
Электрон вполне упорядоченным образом проходит через левую щель. Одновременно он столь же упорядоченно проходит через правую щель. Он направляется к левой щели, но вдруг меняет направление и устремляется к правой. Он петляет вперёд и назад и, наконец, проходит через левую щель. Он отправляется в долгое путешествие к туманности Андромеды, там он разворачивается, возвращается назад и проходит через левую щель на пути к экрану. Он движется и так и этак — согласно Фейнману, электрон одновременно «рыщет» по всем возможным путям, соединяющим пункт отправления и пункт назначения.
Фейнман показал, что каждому из этих путей можно поставить в соответствие некоторое число, и общее среднее этих чисел даст ту же вероятность, что и расчёт с использованием волновой функции. Итак, с точки зрения Фейнмана, с электроном не нужно связывать никакой вероятностной волны. Вместо этого мы должны представить себе нечто столь же, если не более, странное. Вероятность того, что электрон, — который во всех отношениях проявляет себя частицей, — появится в некоторой заданной точке экрана, определяется суммарным эффектом от всех возможных путей, ведущих в эту точку. Этот подход к квантовой механике известен как фейнмановское «суммирование по путям».[16]
Здесь начинает протестовать наше классическое образование: как может один электрон одновременно перемещаться по различным путям, да ещё и по бесконечному числу путей? Это возражение кажется неоспоримым, но квантовая механика — реальная физика нашего мира — требует, чтобы вы держали столь тривиальные возражения при себе. Результаты расчётов с использованием фейнмановского подхода согласуются с результатами, полученными с применением метода волновых функций, которые, в свою очередь, согласуются с экспериментальными данными. Вы должны позволить природе самой определять, что является разумным, а что — неразумным. Как написал в одной из своих работ Фейнман: «[Квантовая механика] даёт совершенно абсурдное с точки зрения здравого смысла описание Природы. И оно полностью соответствует эксперименту. Так что я надеюсь, что вы сможете принять Природу такой, как Она есть — абсурдной».{20}
Однако независимо от того, насколько абсурдной является природа на уровне микромира, при переходе к нашим обычным масштабам любая теория должна приводить к привычным прозаичным событиям. Как показал Фейнман, для движения больших тел, таких как бейсбольные мячи, аэропланы или планеты, каждое из которых является огромным по сравнению с субатомными частицами, его правило определения весов различных траекторий гарантирует, что все траектории, кроме одной, взаимно сократятся при суммировании их вкладов. В действительности, когда дело касается движения классического тела, значение имеет только одна траектория из бесконечного их количества. И это именно та траектория, которая следует из ньютоновских законов движения. Вот почему в нашем повседневном мире нам кажется, что тела (такие, как брошенный в воздух мяч) следуют вдоль единственной, уникальной и предсказуемой траектории из начальной точки в пункт назначения. Но для объектов микромира фейнмановское правило назначения весов траекториям показывает, что свой вклад в движение объекта могут вносить (и часто вносят) многочисленные возможные траектории. Например, в эксперименте с двумя щелями некоторые из траекторий проходят через разные щели, приводя к образованию интерференционной картины. В микромире мы не можем гарантировать, что электрон пройдёт только через одну щель или только через другую. Интерференционная картина и фейнмановская альтернативная формулировка квантовой механики недвусмысленно поддерживают друг друга.
Как разные мнения о книге или фильме могут оказаться полезными для понимания различных моментов этого произведения, так и различные подходы к квантовой механике помогают углубить понимание этой теории. Хотя предсказания метода волновых функций и фейнмановского суммирования по траекториям полностью согласуются друг с другом, в их основе лежат совершенно различные представления. Как мы увидим позднее, для разных приложений тот или иной подход может стать неоценимым средством объяснения.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК