Проблески M-теории
Сегодня точка зрения радикально изменилась. На конференции «Струны-95» Виттен сделал следующее утверждение: если взять теорию струн типа IIA с константой связи, много меньшей 1, и увеличивать константу связи до значения, много большего 1, то физические свойства, которые мы ещё способны анализировать (по существу, свойства насыщенных БПС-состояний), в низкоэнергетическом пределе будут соответствовать свойствам 11-мерной супергравитации.
Когда Виттен объявил о своём открытии, все присутствовавшие в аудитории потеряли дар речи, а позже весть об этом открытии громом пронеслась по всем институтам, где занимаются теорией струн. Почти для всех специалистов в этой области результат был полной неожиданностью. Первая реакция читателя этой книги, возможно, тоже будет напоминать реакцию большинства экспертов: какое отношение может иметь теория, характерная для одиннадцати измерений, к другой теории в десяти измерениях?
Ответ несёт в себе глубокий смысл. Чтобы понять его, нужно описать результат Виттена более точно. На самом деле, сначала проще обратиться к другому тесно связанному с этим результату, полученному чуть позже Виттеном и стажёром Принстонского университета Петром Хофавой для теории E-гетеротической струны. Для этой теории в области сильной связи ими также было найдено описание в терминах 11-мерной теории; это поясняется на рис. 12.7.

Рис. 12.7. При увеличении константы связи E-гетеротической струны появляется новое измерение, и сама струна вытягивается, принимая вид цилиндрической мембраны
Слева на этом рисунке схематически показана теория E-гетеротической струны с константой связи, много меньшей 1. Эта область констант связи рассматривалась в предыдущих главах и изучалась теоретиками на протяжении более десяти лет. При переходе вправо на рис. 12.7 значение константы связи постепенно увеличивается. До 1995 г. теоретикам было известно, что при этом вклады петлевых диаграмм (см. рис. 12.6) будут становиться всё более важными, и при дальнейшем увеличении константы связи весь формализм теории возмущений перестаёт быть справедливым. Но никто не мог даже вообразить того, что при увеличении константы связи проявится новое измерение! На рис. 12.7 это измерение соответствует вертикали. Нужно помнить, что двумерная сетка на рисунке, с которого мы начали обсуждение, представляет все девять пространственных измерений E-гетеротической струны. Новое измерение по вертикали будет десятым пространственным, так что вместе с временным измерением в сумме получается одиннадцать пространственно-временных измерений.
Кроме того, на рис. 12.7 иллюстрируется важнейшее следствие существования этого нового измерения. Структура E-гетеротической струны меняется по мере роста этого измерения. При увеличении константы связи из одномерной петли она растягивается в ленту, а затем — в деформированный цилиндр! Другими словами, E-гетеротическая струна становится двумерной мембраной, ширина которой (протяжённость по вертикали на рис. 12.7) определяется значением константы связи. Более десятилетия теоретики всегда использовали методы теории возмущений, основанные на предположении малости константы связи. Как показал Виттен, в этом предположении фундаментальные объекты микромира выглядят и ведут себя подобно струнам, даже если у них имеется скрытое второе пространственное измерение. Если отказаться от предположения о малости константы связи и рассмотреть физические характеристики E-гетеротической струны при больших константах связи, второе измерение станет явным.
Это утверждение не обесценивает ни одного из выводов предыдущих глав, но побуждает рассмотреть их в рамках нового формализма. Возникает, например, вопрос, как можно состыковать новые результаты с тем, что в теории струн требуется одно временное и девять пространственных измерений? Что же, как обсуждалось в главе 8, это ограничение возникает при расчёте числа различных направлений, в которых может колебаться струна, и число измерений выбирается так, чтобы квантово-механические вероятности гарантированно имели осмысленные значения. Новое измерение не является измерением, в котором может колебаться E-гетеротическая струна, так как оно зафиксировано в самой структуре «струны». Кроме того, в формализме теории возмущений, который использовался физиками для вывода ограничения на число пространственно-временных измерений, предполагалось, что константа связи E-гетеротической струны мала. И хотя это было осознано гораздо позднее, в таком предположении неявно используются два взаимосогласованных приближения: малая ширина мембраны на рис. 12.7, при которой она выглядит, как струна, и малый размер одиннадцатого измерения, не влияющий на вид уравнений теории возмущений. В рамках этой приближённой схемы мы вынуждены представлять себе Вселенную десятимерной и заполненной одномерными струнами. Теперь мы видим, что она 11-мерная и заполнена двумерными мембранами.
По техническим причинам, впервые Виттен столкнулся с одиннадцатым измерением при исследовании сильной связи струны типа IIA, для которой ситуация вполне аналогична. Как и в случае E-гетеротической струны, размер одиннадцатого измерения в случае струны типа IIA определяется значением её константы связи. При увеличении этого значения новое измерение расширяется. По мере расширения, однако, струна типа IIA превращается в «велосипедную камеру» (см. рис. 12.8), а не в ленту, как в случае E-гетеротической струны.

Рис. 12.8. По мере увеличения константы связи для струны типа IIA струны расширяются, превращаясь из одномерных петель в двумерные объекты, похожие на велосипедную камеру
И снова, согласно Виттену, традиционные представления физиков о струнах типа IIA как об одномерных объектах, имеющих длину, но не имеющих толщины, есть следствие использования ими формализма теории возмущений, в котором константа связи струны предполагается малой. Если законы природы требуют, чтобы константа связи действительно была малой, то это приближение оправдано. Однако результаты Виттена и других физиков, полученные в ходе второй революции в теории суперструн, убедительно свидетельствуют о том, что «струны» типа IIA и E-гетеротические «струны» имеют фундаментальную структуру двумерных мембран, живущих в 11-мерной вселенной.
Но что представляет собой 11-мерная теория? Согласно Виттену и другим исследователям, при низких (по сравнению с планковской) энергиях она аппроксимируется почти позабытой всеми 11-мерной квантово-полевой теорией супергравитации. А как же тогда описать эту теорию при высоких энергиях? Сейчас этот вопрос тщательно исследуется. Как показано на рис. 12.7 и 12.8, в такой 11-мерной теории существуют двумерные протяжённые объекты — двумерные мембраны. Как мы вскоре увидим, важную роль играют и протяжённые объекты других размерностей. Однако об этой 11-мерной теории ничего не известно, кроме набора разнородных фактов. Являются ли мембраны её фундаментальными объектами? Каковы её определяющие свойства? Благодаря каким её свойствам она может быть связана со знакомой нам физикой? Если соответствующие константы связи малы, то лучшие ответы, которые можно дать сейчас, уже описаны в предыдущих главах, так как при малых константах связи мы возвращаемся обратно к теории струн. Но для больших констант связи в настоящее время ответов не знает никто.
Для этой 11-мерной теории, что бы она собой ни представляла, Виттен придумал рабочее название: M-теория. Все расшифровывают это название по-разному. Вот примеры: мистическая теория, материнская теория («мать всех теорий»), мембранная теория (так как мембраны в любом случае играют в ней роль), матричная теория (после недавних работ Тома Бэнкса из университета Ратгерса, Вилли Фишлера из Техасского университета в Остине, Стивена Шенкера из университета Ратгерса, Сасскинда и других, предложивших новую интерпретацию теории). Однако и без точной расшифровки названия или знания её свойств уже сейчас ясно, что M-теория даёт основу для объединения всех пяти теорий струн.
M-теория и паутина взаимосвязей
Есть старая притча о трёх слепцах и слоне. Первый слепец ощупывает бивень слона и говорит, что чувствует что-то гладкое и твёрдое. Второй держится за ногу и описывает что-то шероховатое и мускулистое. Третий слепец держит слона за хвост и говорит о чём-то гибком и хилом. Слыша описания других слепцов, каждый из них думает, что держится за другое животное. Много лет физики были столь же слепы и думали, что разные теории струн действительно являются разными. Но теперь, благодаря второй революции в теории суперструн, наступило прозрение, и они поняли, что все пять теорий струн являются частями тела одного огромного «слона» — M-теории.
В этой главе мы обсудили, как изменилось наше понимание теории струн при выходе за рамки теории возмущений, неявно использовавшейся в предыдущих главах. На рис. 12.9 подведён итог тем взаимосвязям, которые обсуждались до этого момента. Стрелками на этом рисунке обозначены дуальные теории.

Рис. 12.9. Стрелки обозначают отношения дуальности для теорий
Видно, что мы имеем паутину взаимосвязей, но она соткана ещё не полностью. Включая дуальности из главы 10, можно довести дело до конца.
Вспомним о дуальности, возникающей при замене радиуса циклического измерения R на радиус 1/R. Выше мы слегка сгладили один аспект этой дуальности, но теперь его нужно рассмотреть подробнее. В главе 10 обсуждались свойства струн во вселенной с одним циклическим измерением; при этом не указывалось конкретно, с какой из пяти теорий струн мы работаем. Как утверждалось, взаимная замена колебательных мод струны на топологические позволяет переформулировать описание (в рамках теории струн) вселенной с циклическим измерением радиуса 1/R в терминах вселенной с циклическим измерением радиуса R. Факт, который был нами опущен, состоит в том, что теории струн типов IIA и IIB, а также теории E- и O-гетеротических струн в действительности не переходят сами в себя, а меняются местами при замене радиусов. Поэтому применительно к этим теориям точная формулировка дуальности при замене радиусов такова: законы физики в теории струн типа IIA во вселенной с циклическим измерением радиуса R идентичны законам физики в теории струн IIB во вселенной с циклическим измерением радиуса 1/R. Аналогичное утверждение справедливо для теорий E- и O-гетеротических струн. На выводах главы 10 такая формулировка не отражалась, но в данном обсуждении она играет важную роль.
Дело в том, что с учётом дуальности при замене радиусов в теориях струн типов IIA и IIB, а также с учётом той же дуальности для теорий O- и E-гетеротических струн можно достроить до конца паутину взаимосвязей, как показано на рис. 12.10 пунктирными линиями.
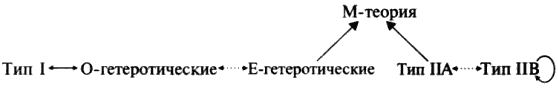
Рис. 12.10. С учётом дуальностей, включающих геометрию пространства-времени (как в главе 10) все пять теорий вместе с M-теорией связываются воедино паутиной дуальностей
Видно, что все пять теорий, а также M-теория, дуальны друг другу. Все они скреплены в единую теоретическую конструкцию и дают пять разных подходов для описания одной и той же физики, лежащей в основе этой формулировки. Для различных приложений может быть более удобным язык той или иной теории. Например, с теорией O-гетеротических струн в случае слабой связи работать гораздо удобнее, чем с теорией струн типа I в случае сильной связи. Тем не менее эти теории описывают одни и те же физические явления.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК