Глава 12. НА ЯЗЫКЕ ГРАФИКОВ

Вклад Германа Минковского

Любознательный человек не может остаться равнодушным, постигая относительность расстояний и времени. Хочется еще и еще раз убедиться в этой неожиданной истине, представить ее в примере, в событии, в чертеже.

Сразу после провозглашения принципа относительности люди науки начали азартно осваивать новый взгляд на движение.

Тут было над чем подумать не только физику, но и математику и философу. Как из рога изобилия, сыпались возражения. Объявились ярые враги «нелепостей» странной теории. Даже в кругу сторонников Эйнштейна не умолкали споры. Ученики перемешались с учителями, каждый стремился найти новую черту, новую подробность, новое истолкование теории относительности. И находили. Решали только что придуманные парадоксальные задачи, доказывали поразительные теоремы.

Одна из работ того времени стала особенно заметной вехой в развитии релятивистской физики. Речь идет о геометрической интерпретации идей теории Эйнштейна, о представлении ее в графиках и диаграммах. Автором этого оригинального подхода, ставшего затем неизменно принадлежностью и монографий, и учебников, и популярных брошюр, был немецкий математик Герман Минковский, один из старейших коллег Эйнштейна, его университетский учитель.

Стоит заметить, что Минковский не питал никакого интереса к личности Эйнштейна. Более того, старый профессор однажды объявил, что ни за что не поручил бы Эйнштейну разработку геометрической интерпретации его же теории по той причине, что Эйнштейн, как полагал Минковский, был человеком необязательным, ибо «вечно пропускал университетские лекции».

Это не помешало Минковскому быть энтузиастом эйнштейновских воззрений и великолепным их истолкователем.

В 1908 году, незадолго до смерти, Минковский прочитал в немецком научном обществе лекцию о мире, пространстве, времени, в которой произнес знаменитую фразу: «Отныне и навсегда пространство и время превращаются лишь в тени, и только некий род единства того и другого сохраняет независимое существование».

Очень коротко и упрощенно мы попробуем разобраться в интерпретации Минковского. Причем перед самыми ленивыми из читателей я вынужден извиниться: на ближайших страницах совершенно неизбежны не очень длинные (и, мне кажется, вовсе не трудные) рассуждения в духе школьных геометрических теорем[9].

Москва — Ленинград

Сперва несколько слов о совсем-совсем простом.

Что случилось на Октябрьской железной дороге такого-то числа с полуночи до шести часов утра?

Было довольно много всевозможных событий. Поезда отправлялись, встречались друг с другом, делали короткие и длинные остановки, прибывали в пункт назначения и т. д. Все это можно подробно выяснить в железнодорожном расписании — весьма сложной таблице со множеством граф, клеточек, слов, цифр. Но гораздо проще поступить иначе: взглянуть на графическую диаграмму движения.

График — очень удобная вещь. Вместо того, чтобы писать уйму слов и цифр, проводится линия на листе миллиметровки — и все, что нужно объяснить, объяснено.

Вот, например, фраза: «Точно в полночь от перрона в Москве отошел экспресс, который двигался затем без остановок равномерно со скоростью сто километров в час и ровно в шесть часов утра прибыл в Ленинград». На графике это громоздкое изречение заменяется прямой линией.

В самом деле, диаграмма такова:

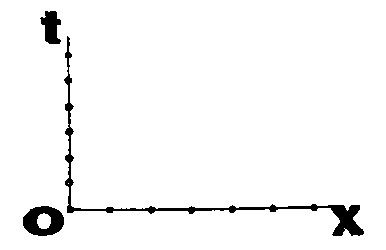
Ось х—условное изображение расстояния, которое проходит поезд. Ось t — геометрический образ времени движения. Обе оси поделены на единицы длины и времени в уменьшенном масштабе.

Сначала диаграмма пуста. Но вот пробило полночь, и из Москвы вышел экспресс. Через час он уже в ста километрах от Москвы, через два — в двухстах, и т.д.

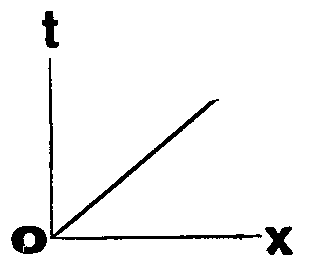
Чтобы построить график, из точек оси х, соответствующих началам каждой новой сотни километров, проводим вспомогательные линии, параллельные оси t, а из точек начала каждого нового часа оси t — параллельные оси х.

Там, где соответствующие друг другу вспомогательные линии пересекутся, получатся точки графика. Поезд в них характеризуется двумя признаками: «там» и «тогда».

Пока все ясно, никаких трудностей. Легко согласиться, конечно, и с тем, что угол между осями не обязательно прямой. Если он тупой, график пойдет так:

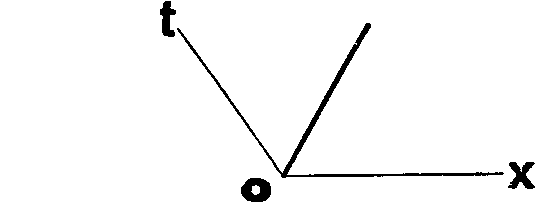
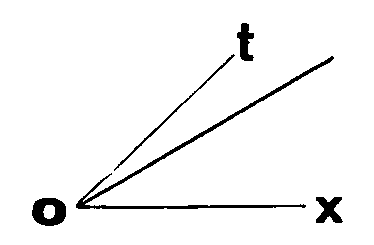
Теперь храбро (хоть и чуть преждевременно, но это ради понятности) применим терминологию Минковского.

Точки графика — это мировые точки. Сам график — мировая линия. И, наконец, мир — нарисованная нами диаграмма.

Как видите, в старое слово «мир» Минковский вложил оригинальный физический смысл: графическое изображение на диаграмме событий сразу в пространстве и времени. Здесь это объединение пространства и времени чисто формальное, продиктованное требованием удобства и лаконизма. Но зато как велики эти удобства!

Мир железной дороги

Предлагаю вам внимательно разглядеть следующую картинку:

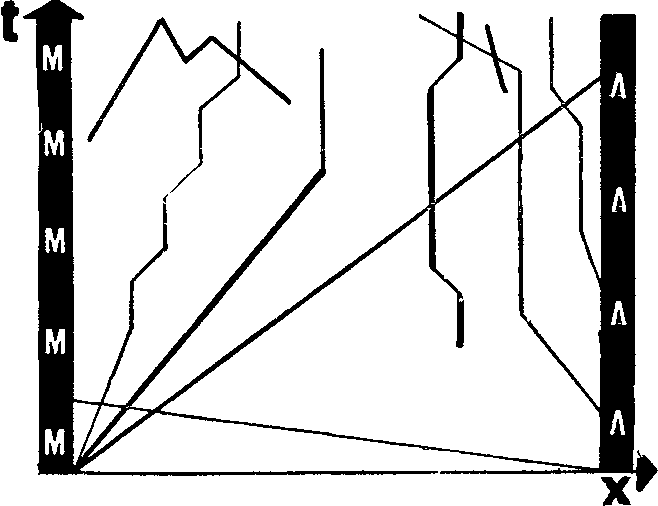
Все события, происшедшие за четверть суток на Октябрьской дороге, нашли здесь точное отображение. Сэкономлена масса бумаги и типографской краски. Каждую мировую линию вы при желании расшифруете словами и цифрами, составив, таким образом, длинные перечни событий.

Есть тут поезда скорые, идущие быстро и почти без остановок; есть почтовый поезд, еле плетущийся, останавливающийся «у каждого куста»; есть товарняки, которые больше стоят, чем едут. Кроме того, есть нечто весьма быстрое — добравшееся из Ленинграда в Москву за час (я думаю, это самолет, летевший вдоль дороги).

На диаграмме хорошо заметен тот факт, что все в мире движется не только в пространстве, но и во времени. Движению только во времени дается выразительная интерпретация: мировая линия становится параллельна оси t. Вон, в середине, какой-то товарняк застрял в Бологом, но мировая линия его тянется вверх. Не сдвигаясь с места, он путешествует в будущее.

Такие же параллельные оси времени мировые линии можно было бы нарисовать и для рельсов, и для шпал, и для каждой станции. Я ограничился тем, что попросил нарисовать их только для Москвы и Ленинграда. Вышли не линии, а столбики — потому что оба города отнюдь не точки, а имеют внушительные размеры. Продвигаясь во времени, длины городов как бы размазываются в полоски.

Попробуйте сами

Есть на последней диаграмме график с подвохом — специально, чтобы вы над ним подумали. Вон он в левом верхнем углу, что-то вроде буквы «М». Если нашли, задержите чтение и попытайтесь сообразить, какими словами, какой последовательностью событий можно его расшифровать. Стоп! Дальше пока не читать!

Думайте...

Кто сам догадался — молодец.

Этот график — не одна мировая линия, а четыре. Каждый прямой отрезок — особый поезд. Но идут они в разных направлениях. Первый слева — к Ленинграду, второй — к Москве, третий — тоже к Ленинграду, четвертый — к Москве. Первый встречается со вторым, второй выходит из одного пункта с третьим одновременно, но в разные стороны, а в конце своего пути встречается с четвертым. Почему такое раздробление? Во исполнение закона причинности. Если бы второй и четвертый поезда шли к Ленинграду, они двигались бы в обратном времени, путешествовали бы в прошлом. И прибыли бы в пункт назначения до ухода из пункта отбытия, что невозможно, ибо принцип причинности нерушим.

Двигаться в мире разрешено только так, чтобы время текло в одну сторону — вперед. По оси расстояний можно кататься туда и обратно — вправо и влево, а по оси времени лишь в будущее, то есть, на нашей диаграмме, вверх. Поэтому каждый прямой отрезок буквы «М» должен проходить снизу вверх.

Подвохи еще не кончились. Вот вопрос: что произошло в точках встреч мировых линий, в вершинах «М»?

Там случились, надо полагать, страшные крушения, или, в лучшем случае, в этих точках поезда были очень быстро расформированы. Так или иначе, но они наверняка исчезли.

Ведь если бы первый поезд просто остановился, встретившись со вторым, то его мировая линия не пропала бы, а потянулась в будущее но прямой, параллельной оси времени. Но линии нет. Значит, сошедшиеся поезда тоже исчезли. Что и требовалось доказать.

Честно говоря, сейчас была предложена довольно трудная для новичка логическая задача. Кто не решил ее, пусть не печалится. Хорошо, если он хоть разобрался в объяснении.

Простенькая фигурка на диаграмме рассказала нам, как видите, весьма поучительную логическую историю. Из нее полезно извлечь мораль: рисуя мировые линии, помните, что у них есть направления — разрешенное и запрещенное законом причинности.

Идущий поезд „неподвижен"

Бездельничая в купе, пассажиры говорят:

До Бологого пять километров.

Остался час до Ленинграда.

В таких сентенциях отсчет времени и расстояний всегда ведется от поезда. Это понятно. Пусть где-то на пути неожиданно лопнул рельс. Машинисту и пассажирам жизненно важно знать, далеко ли и с какой стороны это произошло именно от поезда. Расстояние же лопнувшего рельса от Москвы или Ленинграда для обитателей поезда несущественны.

Поэтому пассажиры и машинист, пользуясь отсчетами «от поезда», склонны неосознанно применять принцип относительности и чувствовать себя неподвижными, а движущейся считать дорогу вместе со всеми станциями, Москвой и Ленинградом. Это им удобно. С этой точки зрения они могут нарисовать диаграмму движения. Как же изменится ее вид?

Да никак не изменится. Только система отсчета из прямоугольной сделается косоугольной. Старая ось времени превратится в мировую линию Москвы. Мировая линия поезда станет новой осью времени t, на которой увеличится масштаб, то есть длина отрезков, изображающих часы или минуты. Ось расстояний останется без перемен. А положение относительно поезда событий (мировых точек) определится по прежним правилам: в пересечении вспомогательных линий, параллельных осям расстояний и времени.

Взгляните:

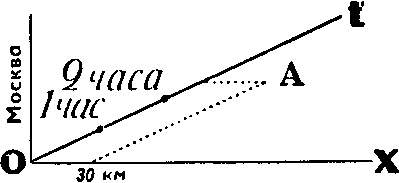
Здесь мировая точка А — удар молнии в рельс. Как видно из построения, он произошел в 2 часа 35 минут в тридцати километрах перед поездом.

Диаграмма дает возможность пойти навстречу не только обитателям экспресса Москва — Ленинград. Каждый поезд вправе объявить себя неподвижным, и это вполне поддается геометрическому изображению: надо только его мировую линию переименовать в ось времени. Для поездов, выходящих из Москвы (а заодно и для самой Москвы), пусть получится такая картина:

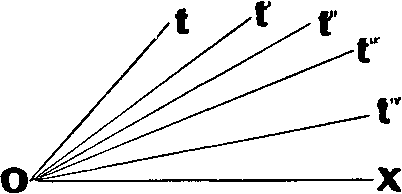
Все оси времени (Ot, Ot’, Ot’’, Ot’’’ и т. д.) тут равноправны, а ось расстояний у них общая.

Различие систем чисто условное — в масштабах времени. Как же находить эти масштабы?

Отметив на одной из осей времени отрезок ОB, соответствующий часу, проводим через точку В линию, параллельную оси расстояний. На всех остальных осях времени она отметит одновременные события, а значит, отсечет отрезки, равные часу.

Эта линия, указывающая масштабы систем отсчета, называется калибровочной.

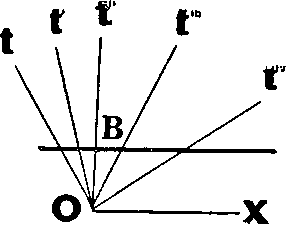Вот, пожалуй, и готов пространственно-временной мир Октябрьской железной дороги. Полную его картину (для обоих направлений) вы при желании легко нарисуете сами. В этом мире царит ньютоновское абсолютное пространство (ось расстояний единственная на все поезда), присутствует абсолютное время (любая линия, параллельная оси расстояний, проходит через события, абсолютно одновременные во всех системах отсчета), узаконен галилеевский принцип относительности.

Так выглядит диаграмма равномерных прямых движений, которые медленны по сравнению со светом. Мир доэйнштейновский.

Четыре шага

Ну, а какова диаграмма эйнштейновского мира?

Ее построим постепенно, в несколько шагов.

Шаг первый. Рисую оси Москвы. Ускоряю поезда в миллионы раз. Они мчат со скоростями, сравнимыми со скоростью света. Из Москвы в Ленинград попадают за малые доли секунды. Их мировые линии сжались в плотный пучок.

Графики идут так густо, что разобрать ничего не возможно. Как быть?

Шаг второй. Надо растянуть оси времени. Тогда нижняя часть диаграммы вытянется вверх, и можно будет сообразить, как она устроена. Для этого придется помножить время на какую-нибудь очень большую величину, обязательно постоянную для всех систем отсчета. Такова скорость света: и велика, и одинакова для любых наблюдателей. Ее удобно взять множителем.

Поэтому вместо осей t рисуем оси ct:

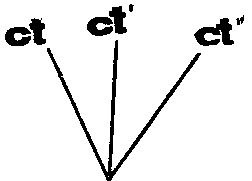
Низ диаграммы пока неясен.

Шаг третий. Из Москвы в Ленинград посылаем телеграмму. Сигнал летит по проводам со скоростью света (будем считать так, хоть это и не совсем точно). Благодаря множителю с на оси времени мировая линия света (сигнала телеграммы) ляжет точно по биссектрисе угла между осью времени и осью расстояний Москвы: ведь за секунду, которая на оси времени имеет длину с, свет пробежит ту же длину с по оси расстояний. Так мы вносим первый штрих в нижнюю часть диаграммы — для оси ct чертим ось х:

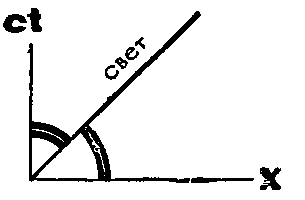
Шаг четвертый. Рассуждения третьего шага годятся для любых систем отсчета. У каждой мировая линия света (говорят также— световая линия) должна делить пополам угол между осями времени и расстояний. Так и рисуем:

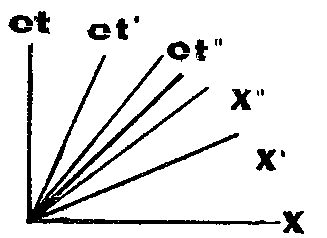
Ось расстояний, как видите, расщепилась. У всякой системы отсчета — собственная длина пути. Ничего неожиданного: в теории относительности так оно и есть.

Еще два шага

Внимание! Предстоит нелегкое место. Сосредоточьтесь. Речь пойдет о калибровочных линиях сверхбыстрого мира — тех, что отсекают масштабы на осях.

В диаграмме медленных движений требовалась только калибровочная линия времени, потому что ось расстояний (а значит, и единица длины) там была одна на все поезда. И тянулась калибровочная линия времени параллельно единственной оси расстояний. Это было привычно и понятно, ибо означало: в мире существует абсолютная одновременность и единое всеобщее время.

Теперь одной калибровочной не хватит. Ось расстояний расщепилась — значит, пропала абсолютная одновременность, а с нею ушли абсолютное время и абсолютная длина. Нам придется построить две калибровочные линии, чтобы одна отсекала масштабы времени на осях времени разных систем отсчета, а другая — масштабы длины на осях расстояний.

Шаг пятый. Поищем калибровочную линию времени. Рецепт прежний: она должна отсекать на осях времени концы секунд, начавшихся вместе в мировой точке О. Но если раньше моменты окончания одновременно начинавшихся секунд были абсолютно одновременны, то теперь этого нет. Зато появилась относительная одновременность, чем мы и воспользуемся.

Помните, как определяется относительная одновременность? Это было при игре «Кто первый?» и дуэли Онегина и Ленского в десятой главе. Надо, чтобы в середине прямого отрезка совпали световые сигналы от событий, произошедших на разных его концах. Сигналы совпали — значит, события одновременны.

Заметим на оси ct точку A, отсекающую ровно секунду от начала счета времени (точка О). Допустим далее, что в точке A’ лежащей на оси ct’ совпали сигналы, пришедшие из A и из A₁, причем А₁ — некое событие, происходящее в системе х’,ct’ на том же расстоянии от А', как и A, но с противоположной стороны. При этом условии и линия АА₁ должна быть параллельна оси x’ и в точке A' делиться пополам. Налицо признак относительной одновременности — события A и А₁ одновременны в системе х’,ct’.

Представим затем, что аналогичным образом определена одновременность событий А₁ и A₂ в системе х", ct", событий A₂ и A₃ в системе x’’’’, ct’’’ и т. д.

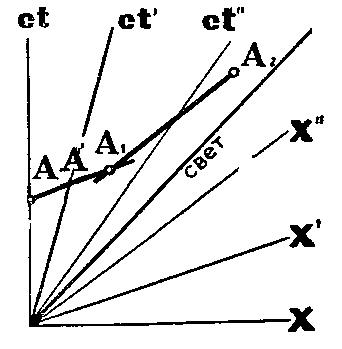
о

Догадываетесь, что достигнуто этим хитроумным построением?

Отыскано графическое правило нахождения относительной длительности секунды в разных системах отсчета на диаграмме. Геометрический рецепт, по которому узнают масштаб хода часов, движущихся относительно друг друга равномерно по одной прямой.

Соединим плавной линией точки A, A₁, A₂, A₃ и т. д.— и выйдет калибровочная линия времени. Это не прямая, как в «медленной» диаграмме, а кривая, называемая гиперболой:

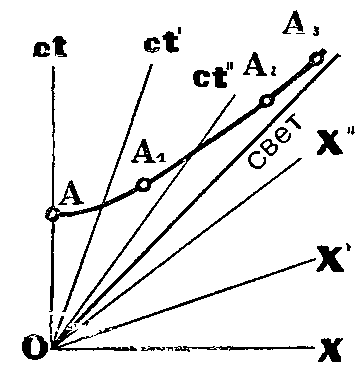
С ростом скорости системы отсчета (сверхбыстрого поезда или ракеты) калибровочная линия времени уходит в бесконечность. Наглядно видно, как долго тянутся секунды «быстрых» систем с точки зрения «медленных». А свет живет в бесконечно длинных, остановившихся секундах. Для света движение мгновенно!

Шаг шестой. Я щажу утомленного геометрией читателя и великодушно освобождаю его от новой порции умственного напряжения. Поверьте на слово, что точно так же, как калибровочная линия времени, строится калибровочная линия расстояний в нижней части диаграммы.

Почти окончательно мир сверхбыстрых движений (происходящих на прямой дороге в одну сторону) предстает перед нами в виде такого чертежа:

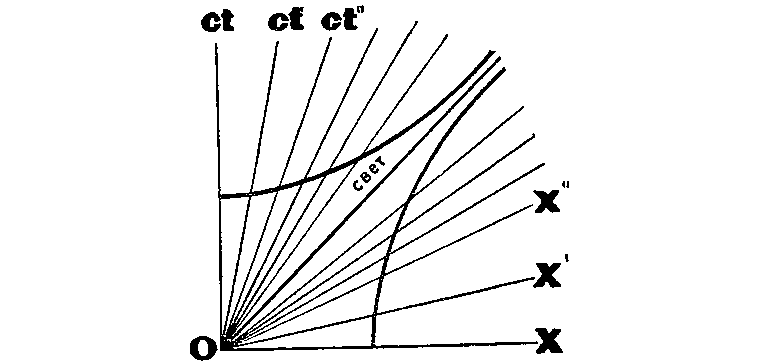
Значительно хитрее, чем в старой доброй классике.