Глава 22. ВДОЛЬ ПРОСТРАНСТВА

От окна до киоска

Я уже не блин. Мне возвращена высота. Я покинул мир тесных, бесконечно тонких площадей, живу, как и вы, в объеме, в глубоком, раздольном пространстве. Хорошо! Есть где развернуться! Можно не только ползать, но и прыгать и летать. Это очень приятно.

Но мне не до развлечений. В бытность блином я привык беспрерывно исследовать кривизну своего мира, и теперь меня тянет заняться тем же в пространстве.

Прежде всего я намереваюсь придумать способ облачения пустоты в «пифагоровы штаны» и примерки к ней «треугольной шляпы».

Как это сделать?

Вот легонькая задачка из школьной стереометрии.

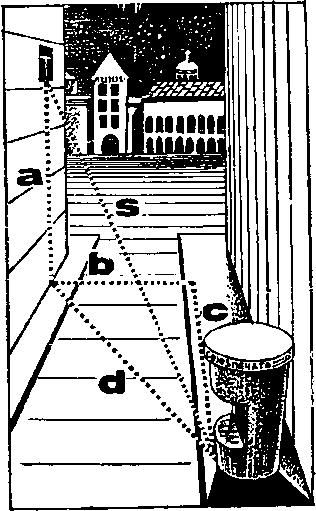
От моего окна (на пятом этаже) до газетного киоска на противоположной стороне улицы «напрямую» S метров. По тротуару от моего дома с метров, b — ширина улицы, а — высоты моего окна. Требуется найти S, не мешая уличному движению — не протягивая из окна к киоску туго натянутой веревки, а вычислив это расстояние через a, b и с.

Решение наипростейшее: считаем, что стена дома составляет прямой угол с поверхностью тротуара, что переход через улицу перпендикулярен к ней самой, пренебрегаем кривизной земной поверхности и дважды применяем теорему Пифагора. Так добываем формулу:

S² = а² + b² + с².

Вышло очень похоже на теорему Пифагора, но уже не для плоскости, а для пространства. Для кратчайшего расстояния S, прокладываемого «через пустоту».

Разумеется, a, b и с можно менять, можно строить около расстояния S самые разнообразные прямоугольные треугольники. И по традиционной школьной геометрии квадрат расстояния во всех случаях будет равен сумме квадратов его трех взаимно перпендикулярных координатных отсчетов. Поэтому выражение теоремы Пифагора считается главным инвариантом евклидовой геометрии.

Очень хорошо. От метрики плоскости мы шагнули к метрике пространства. Но вот существенная тонкость.

Наше решение выглядит непогрешимым и единственно возможным. Однако оно предполагает самоочевидное, как кажется, условие: в пространстве существуют плоскости. Именно поэтому мы считали себя вправе дважды применить плоскую теорему Пифагора (она, как говорилось, годится в этом простейшем виде лишь для плоскостей).

На том же условии нетрудно доказать и другую теорему — о том, что не только в плоских, но и пространственных треугольниках сумма углов составляет два прямых. Раз уж, согласно Евклиду, через любые три точки пространства можно провести плоскость, то и любой пространственный треугольник обязан быть плоским. Но так ли обстоит дело в действительности? Будут ли впору «прямые» штаны и «прямая» шляпа реальному пространству?

Что ж, из всего этого следует как будто немудрящий рецепт облачения пустоты в «пифагоровы штаны» и «треугольную шляпу». Надо проделать измерения длин и углов в реальных пространственных треугольниках. И таким способом «испытать пространство на кривизну».

Облачение пустоты

Ночью, чтобы не мешать уличному движению, я протягиваю веревку из своего окна к далекому киоску. Тщательно измеряю расстояние S. Столь же точно измеряю длины а, b и с. Возвожу их в квадрат, складываю, сравниваю. Вышло подтверждение формулы

S² = а² + b² + с² — значит, в пространстве можно провести плоскости и прямые, значит, пространство плоское, евклидово.

Или так. Еду на Кавказ. Стягиваю тугими канатами три горные вершины. Измеряю в этом треугольнике углы, складываю их. Получилось в сумме два прямых — есть еще одно доказательство того, что пространство плоское.

Ну, а если эти эксперименты приведут к другим результатам? Если S² не совпадет с а² + b² + с²? И сумма углов кавказского треугольника не даст двух прямых? Очень нелегко, очень непривычно допустить подобное. Разум упрямо противится даже мысленно позволить столь странный итог пространственных измерений.

Однако вопреки протестам интуиции заставим себя вообразить, что расхождения все-таки обнаружились. Что это может значить?

Когда подобное случалось на поверхности, вывод был очевиден: поверхность имеет кривизну. А когда нарушения традиционной теоремы Пифагора объявятся в пустоте, резонно будет сказать, что это доказывает кривизну пространства. Прежде, будучи блином, я с помощью метрических теорем определял, какова моя поверхность, не сходя с нее. Теперь, став объемным геометром, я хочу совершенно аналогичным способом узнать, каково пространство: насколько и как оно искривлено. И снова—не выходя из него!

На сфере или седле я не мог построить плоскость и провести идеальную прямую линию. Вместо нее у меня выходили геодезические линии — прямейшие, но не прямые. Именно по ним шли кратчайшие расстояния между точками. Подобно этому, в кривом пространстве я не могу построить ни идеальной прямой, ни идеальной плоскости. Вместо плоскостей проведутся поверхности минимальной кривизны, а вместо прямых опять появятся геодезические линии — прямейшие, но не прямые. Однако изнутри, из пространства, непосредственно увидеть искривление его невозможно, потому что тамошние жители сделают кривыми все свои линейки и другие эталоны прямизны — подгонят их к располагающимся по геодезическим линиям световым лучам, натянутым нитям, путям инерционного полета тел, не подверженных действию сил, и т. д. Поверхности минимальной кривизны будут выглядеть плоскостями. Только исследования параллельных линий да метрические эксперименты помогут определить эту странную, почти невообразимую кривизну пустоты.

Трудновато? Да, нелегко.

Геометрическая возможность неевклидового пространства была неожиданным откровением науки XIX века.

Это открытие, сделанное в 1825 году, принадлежит гениальному русскому математику Николаю Ивановичу Лобачевскому.

Два варианта кривизны

Итак, мы с вами добрались до кривого пространства. Научились, кажется, устанавливать изнутри его сам факт кривизны: об этом может свидетельствовать нарушение евклидовых метрических теорем.

Геометры идут дальше: они умеют предсказывать, как именно изменится теорема Пифагора и сумма углов треугольника в пространствах, искривленных по-разному. Рассуждения похожи на те, что я вел, будучи блином на неизвестной поверхности. Например, если а² + b² + с² меньше, чем S², а сумма углов треугольника меньше двух прямых («пифагоровы штаны» и «треугольная шляпа» для пустоты «малы»), то пространство гиперболическое. Вместо плоскостей в нем седловидные поверхности, вместо прямых — гиперболы. Этот вариант неевклидовой геометрии и был разработан Лобачевским.

Другая геометрическая система, развитая замечательным немецким математиком Георгом Риманом, получится, если а² + b² + с² выйдет больше, чем S², а сумма углов треугольника превысит два прямых. Эта геометрия называется эллиптической. В ней вместо плоскостей — поверхности вроде яичной скорлупы или мяча, вместо прямых — дуги больших эллипсов или, соответственно, больших кругов.

Позволю себе повторить еще раз: в плавно искривленном пространстве все геодезические линии представляются прямыми. «Истинных» же прямых там нет, их невозможно провести. Любая неизбежно согнется, как обязательно согнется нить, натянутая по сфере. Причем, если пространство искривлено неравномерно, в разных местах по-разному, то и прямейшие геодезические линии в разных точках согнутся неодинаково. При движении вдоль геодезической ее «волнистость», конечно, незаметна. Всюду эта линия выглядит одинаково прямехонькой. Однако стоит испытать в разных местах метрические правила, как обнаружатся изменения, отклонения от привычной евклидовой «нормы».

Короче говоря, в неравномерно-неевклидовом пространстве от точки к точке меняется метрика, приемы определения расстояний. Меняется теорема Пифагора. В общем виде простая формула ее заменяется более сложной, включающей величины, которые характеризуют кривизну пространства в разных его местах. И, как следствие, в разных местах такого пространства оказываются разными длины предметов, кратчайшие расстояния между точками.

Вот такие чудеса допускают геометры в неевклидовом пространстве!

Сфера Пуанкаре

Еще диковина: некоторые неевклидовы пространства могут быть конечными, хоть и безграничными. Расстояния там не превышают некоего определенного значения и, соответственно, не могут существовать сколь угодно большие объемы.

Подобно тому, как яйцо или мяч обладают безграничной поверхностью, но ограниченной площадью, эллиптическое пространство не имеет границ и тем не менее имеет конечный объем. Искривляясь оно как бы замыкается на себя!

Странно? Очень.

Но все же доступно наглядному моделированию.

Французский математик Анри Пуанкаре один из предшественников Эйнштейна, ухитрился придумать любопытную модель замкнутого сферического пространства. Вот что он советует вообразить.

В шаровом сосуде находится некая среда, в которой плавают предметы и существа, наделенные весьма фантастическими свойствами. При охлаждении и среда и предметы абсолютно одинаково сжимаются, причем при нуле градусов обращаются в точки. Кроме того, световые лучи в этой среде преломляются тем сильнее, чем ниже температура. Шар снаружи заморожен до нуля градусов. А изнутри, из центра, разогрет. И от центра к периферии температура плавно снижается. Еще условие: существо в шаре не должно ощущать перемен температуры. Ему всегда «не жарко, не холодно». Вот и все.

По вашей командировке я обретаю указанные свойства, переселяюсь в шар Пуанкаре (пусть висящий где- то в космосе, в невесомости) и, допустим, обитаю в нем в полном одиночестве. Тем не менее я замечаю вокруг множество человеческих фигур. Всюду я вижу себя и только себя — и впереди, и сзади, и со всех сторон. Световые лучи идут замкнутыми путями. Приближаясь к краям шара, они, плавно преломляясь, заворачивают внутрь, так что эти края невозможно увидеть, даже находясь совсем рядом с ними. Завернув, лучи возвращаются туда, откуда вышли. Вот и получается, что передо мной — моя спина, надо мной — подошвы моих ног, подо мной — моя макушка. Стреляя вперед из светового пистолета, я, если захочу, попаду в собственный затылок.

Разумеется, луч представляется мне прямым. Считая его эталоном прямизны, я не замечаю кривизны своего пространства. Ее нельзя обнаружить и движением: шагая вдоль луча, я открываю лишь существование предельно большого расстояния, так как вскоре возвращаюсь к месту старта. Стенки шара мне совершенно недоступны. Когда я подхожу к ним, то сжимаюсь вместе с окружающей средой, и одновременно сжимаются все расстояния вокруг меня, все длины, все высоты. В любой точке шара я не замечаю изменения своих размеров. Поэтому всюду я воспринимаю окружающее пространство так, будто нахожусь в его центре. И не вижу нигде никаких границ своего маленького мирка. Он конечен по объему, но для меня безграничен. Очень красивая модель!

Как это ни парадоксально, шар Пуанкаре, быть может, кое в чем схож с нашей необозримой Вселенной. Но об этом потом.

Обруч и рельс

Полагаю, мы с вами уже созрели для геометрического истолкования анекдота о кривых дровах. Очень просто: если паровоз въезжает из плоского евклидова пространства в любое неевклидово, то прямые дрова автоматически превращаются в кривые.

Наоборот, если паровоз шел в неевклидовом пространстве и дрова в нем, по мнению машиниста и кочегара, были прямыми, то при въезде в евклидово пространство они искривятся.

Кривизна и прямизна предстают перед нами свойствами не абсолютными, а относительными! Каждое из них зависит от точки зрения, от договоренности, продиктованной, правда, не свободным произволом, а геометрическими свойствами пространства. Вообразив, что пространства разной кривизны вложены друг в друга и из одного можно наблюдать другое, относительность кривизны удастся представить вполне наглядно.

Допустим, например, такой случай. Изготовляя шар Пуанкаре, я вмонтировал в него резиновое кольцо. В евклидовом пространстве это кольцо мне представляется безусловно кривым. Но в шаре Пуанкаре оно может стать прямейшим, если вдоль него пойдет луч света. Вместе с тем железнодорожный рельс, для меня прямой как стрела, в сферическом пространстве станет дугой — ведь «прямой» для обитателя шара Пуанкаре световой луч от рельса отклонится. Удивляйтесь, если не устали!

Такова в самых примитивных чертах неевклидова геометрия. Заканчивая беседу о ней, я должен сообщить вам нечто важное и несколько обескураживающее.

Как вы наверняка догадываетесь, описанные в этой главе геометрические странности имеют непосредственное отношение к общей теории относительности, к тяготению, к инерции, в конечном счете — ко все еще не разгаданной нами до .конца загадке падения тел, действию тяжести через пустоту.

Это действительно так. Но связь, к сожалению, далеко не столь проста, как хотелось бы любителям легкого бегства от удивлений. Приготовьтесь к разочарованию. Все, буквально все только что изложенные геометрические рассуждения и примеры в мире Эйнштейна не имеют ни грана физического смысла. Ибо с самого начала этой главы мы с вами разрешили себе непозволительную идеализацию истинного положения вещей — признали возможность мгновенного измерения расстояний. Отсюда выросла физическая небылица: пространство, не зависимое от времени.

На самом деле ничего мгновенного в природе не бывает. Измерения расстояний кроме линеек требуют еще и часов. И строгого соблюдения не только геометрических, но и чисто физических правил, говорящих, в частности, о том, что пространство вообще не может существовать вне времени. В реальном мире пространство и время неразделимы.

Как велики последствия этого, вы скоро поймете.