Глава 15. ЭНЕРГИЯ, СПРЯТАННАЯ В ВЕЩЕСТВЕ

Сколько весит леденец

У меня на ладони леденец. Прозрачно-розовый, весьма аппетитный. Сколько он весит? Пять граммов. Так показывают мои весы. Это все пока ничуть не странно. Но вот удивительно: вместе с тем этот самый леденец весит десять килограммов. Или, если хотите, три тонны. Или тысячу тонн. Сколько пожелаете!

Сказанное надо обосновать.

Во второй главе мы пространно рассуждали о том, что такое масса. Было выяснено, что масса имеет двоякую сущность — она «едина в двух лицах». Во-первых, она — мера количества вещества, притягиваемого Землей. Это тяжелая масса. Во-вторых, она — мера инерции, мера замедления разгона тела под действием силы. Это инертная масса. Обе массы строго равны. Поэтому все тела падают вблизи земной поверхности с одинаковым ускорением g (разумеется, если им ничто не мешает падать, вроде воздуха). Вспомнили? Очень хорошо.

Дабы уверить вас в странных превращениях леденца, надо будет показать, что леденец в каких-то разных условиях по-разному поддается ускоряющему действию сил или по-разному давит на чашку весов. Я считаю себя вправе выбрать какое-либо одно из этих заданий. Исполнив одно, я не забочусь о втором.

Выбираю первое. То есть берусь убедить вас в том, что мой леденец при неких условиях разогнать так же трудно, как при обычных условиях сдвинуть с места железнодорожный вагон, груженный кирпичом. Сразу скажу, каковы эти условия: надо, чтобы леденец, который мне предстоит разогнать, уже двигался относительно меня. Причем очень быстро — почти со скоростью света. Тогда его масса будет для меня сколь угодно велика — тем больше, чем ближе его скорость к скорости света.

Я думаю, тем, кто усвоил дух теории относительности, интуитивно ясно: если леденец невозможно заставить двигаться быстрее света, значит, он сопротивляется сверхбыстрому разгону, и естественно предположить, что это происходит благодаря увеличению его инерции на больших скоростях, то есть, другими словами, благодаря увеличению массы.

Это действительно так. Но это так важно, что должно быть растолковано подробнее.

Голову—на отсечение

Много мудрых слов сказано о том, что человек может и чего не может. Может, пожалуй, больше, чем не может. И, самое главное, может достоверно установить, что именно не может. Что же человеку недоступно?

Ни один из трех миллиардов людей не в состоянии пробежать стометровку быстрее, чем за 9,9 секунды. Впрочем, выйдет эта книжка, и, весьма вероятно, появится мировой рекорд — 9,8, а то и 9,7 на стометровке. Почему бы нет! Никто не даст голову на отсечение, что в спринтерском беге увеличение скорости невозможно.

Но любой современный физик с легким сердцем прозакладывает голову против посула разогнать в вакууме леденец даже не быстрее, а хотя бы до точной скорости света. Такого не случится никогда — ни сегодня, ни завтра, ни через тысячелетия. Нет и не будет в мире подходящей силы, любая окажется мала. Это в равной мере относится к леденцу, к космическому кораблю, к электрону. Предельная — световая — скорость недостижима ни для какого тела, способного, вообще говоря, двигаться медленнее света (сам свет этого, как вы помните, не умеет). И вместе с тем сколь угодно близко подойти к световой скорости не запрещено ни ракете, ни электрону. Сколь угодно близко — но не точно! От любой скорости, как угодно близкой к скорости света, до самой скорости света — дистанция бесконечно огромная, принципиально непреодолимая. Это прямо вытекает из эйнштейновского закона сложения скоростей, о который споткнулся в предыдущей главе необразованный бандит Клио.

Полезно повторить: Клио равномерно двигался относительно Земли со скоростью, которая была лишь на миллиметр в секунду меньше скорости света. Казалось, одно крошечное усилие — и он обгонит световой луч. Но ничего подобного. Вспомнив первый постулат Эйнштейна, Клио мог вообще забыть о своем движении, признать себя неподвижным.

Тогда он понял бы, что не только обгон света ему не удастся, но что даже до прежней скорости ему придется разгоняться заново. С чьей-то точки зрения вы можете, сильно ускорившись, вплотную подойти к скорости света, но, тем не менее, «для себя» останетесь от нее бесконечно далеко.

Итак, к леденцу, летящему в космосе, вдалеке от планет и звезд, я прикладываю силу. Леденец ускоряется. А я, оставаясь «неподвижным», наблюдаю. Сначала, пока скорость мала (вплоть до тысяч и даже десятков тысяч километров в секунду), ускорение тем больше, чем больше приложенная сила и чем меньше масса леденца. Точно соблюдается второй закон Ньютона. Однако дальнейший разгон решительно не подчиняется старому закону. Леденец становится слишком упрямым, неподатливым. Сила прежняя, а ускорение меньше. Выше скорость — труднее дальнейший разгон. У самой скорости света ускорение под действием прежней силы становится таким неуловимо крохотным, что леденец практически перестает разгоняться. Что ж, я неведомым способом увеличиваю силу. В десятки, в тысячи, в миллиарды раз. Трачу титаническую энергию. Но опять эффект мизерный. Скорость почти не растет. Приблизившись вплотную к скорости света, она словно замораживается.

Дело происходит точно так же, как при неудачной попытке бегства в прошлое. Ничего неожиданного нет. Но зато теперь я могу прямо указать на виновницу «сверхньютоновского» упрямства разгоняющегося тела. Это масса. По мере ускорения тела растет его инерция. У самой скорости света ускорить тело практически невозможно, какую бы гигантскую силу ни прикладывать. Значит, инерция, то есть инертная масса, леденца увеличивается к бесконечности.

Все это — с точки зрения любой инерциальной, то есть не испытывающей ускорений, системы отсчета.

Лилипут-лакомка

Вот формула относительности массы. Лаконично и четко она говорит о том, что с чрезмерным многословием пояснялось выше.

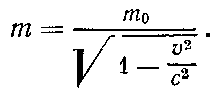
Релятивистская масса m (то есть «движущаяся» масса для «неподвижного» наблюдателя) здесь сравнивается с массой покоя то (то есть с массой, которую измерил неподвижный относительно нее наблюдатель, например я, взвешивающий свой леденец). Можно без особого труда подсчитать, для кого мой леденец весит обещанные десять килограммов. Подставив в формулу соответствующие цифры, получим ответ: для наблюдателя, который движется относительно меня со скоростью 299 999 997 километров в секунду (если считать скорость света равной точно 300 000 километров в секунду) .

Неужели бывают такие расторопные «наблюдатели»? Позволив себе очередную некорректную фантазию, вообразим лилипута, сидящего верхом на каком-нибудь протоне из космических лучей, проносящихся мимо моей ладони. Лилипут — сластена, ему ужасно хочется схватить мой леденец и отправить в рот. Но сделать это ему в две тысячи раз труднее, чем если бы леденец летел рядом с ним. Потому что для него масса леденца увеличилась в две тысячи раз!

Лилипутов-лакомок, увы, не бывает. Зато протоны, несущиеся в космических лучах с подобными скоростями, встречаются нередко. У неподвижного протона масса 1,7·10^-24 грамма. А у движущегося в космических лучах она возрастает для нас, землян, в те же две тысячи раз. Когда физик, лакомый до научных открытий, захочет поймать частицу космических лучей в какой-нибудь прибор, он помнит о релятивистском увеличении массы. Иначе ничего не выйдет, частица не поймается.

Тот же эффект обязательно учитывают, строя ускорители заряженных частиц. Современные ускорители — это машины, в которых полновластно распоряжается физика Эйнштейна.

Так законы теории относительности подтверждаются опытами. Сегодня они стали совершенно неотъемлемой частью экспериментальной физики быстрых движений и высоких энергий.

Что такое „плохо"

Приспело время исполнить обещание о дополнительной порции холодного душа на отчаянных фантазеров (в том числе и на грешную голову автора этой книжки), тех, что с легким сердцем разгоняют ракеты до релятивистских скоростей, заставляют космонавтов за месяцы достигать далеких галактик и без седины в волосах возвращаться домой. К нашему общему огорчению, подобные прожекты, видимо, никогда не осуществятся. И именно потому, что вместе с сокращением релятивистского пути, с замедлением релятивистского времени должна стремительно расти релятивистская масса ракеты. Для ускорений и торможений даже очень скромного по размерам субсветового галактического корабля потребуются неправдоподобно гигантские запасы топлива. Подсчитано: чтобы облететь нашу звездную систему за десятилетия собственного времени, понадобится энергия, равная, самое малое, полному потоку солнечных лучей за... сто миллионов лет! Комментарии излишни.

Жалко, конечно. Остается слабая надежда съездить на субсветовой ракете куда-нибудь сравнительно недалеко— к одной из ближайших звезд, за несколько световых лет.

Если это когда-нибудь удастся, то предварительно будут решены титанической сложности проблемы. Сегодня вряд ли можно обещать что-либо большее. Во всяком случае, наши мысленные эксперименты с космическим пиратством и межзвездной торговлей не имеют никаких шансов обрести хоть мизерную долю реальности. Что, однако, ничуть не подрывает их принципиальную правильность. В них, конечно, крайность, но не доведенная до физического абсурда. Крайность, в которой наглядно обнажается сущность волшебных релятивистских эффектов.

Выходит так. Эйнштейн, с одной стороны, подарил нам сказочную власть над временем и расстояниями, доказав их зависимость от скорости. Но, с другой стороны, в огромной мере лишил нас этой власти, доказав увеличение массы с нарастанием скорости. Хочется посетовать: релятивистские времена и пути — это-де «хорошо». А релятивистская масса — «плохо». Так как будто?

Смотря для кого. Фантазерам, быть может, действительно обидно: срывается (вот беда-то!) затея с путешествием за тридевять галактик. Зато физикам, а вместе с физиками и всему человечеству, совсем недурно. Потому что, как вы скоро увидите, факт относительности массы подсказал Эйнштейну открытие знаменитого закона эквивалентности массы и энергии. Закон, безгранично важный не только для науки, но и для индустриальной, хозяйственной жизни людей. Ибо этот закон сделал нас беспредельными богачами.

Вот вам и «плохо»!

Невидимое и неуловимое

Вернемся к леденцу. Брошенный с околосветовой скоростью, он обладает гигантской массой. Уместно спросить: а за счет чего она появилась, такая большая? Не может же что-то сотвориться из ничего!

Вот упрощенный ответ: энергия, расходуемая на разгон леденца, не только ускорила его, сообщила ему новую добавку скорости, но и увеличила его инерцию. Приобретая дополнительную энергию движения, леденец обзаводился дополнительной массой. Мала была энергия движения леденца — мала и масса. Больше энергия — больше масса. И отсюда можно сделать очень важное заключение: энергия и инертная масса — неразлучные сестры. Та и другая, характеризуя движущуюся материю, изменяются вместе, пропорционально. Собственно, в этом-то и заключается эйнштейновский закон эквивалентности массы и энергии.

Но тут есть тонкость. Когда бакенщик, взяв из рук капитана леденец, «остановит» его и отправит себе в рот, масса леденца для бакенщика не пропадет, пять граммов ее останутся. А энергия механического движения леденца относительно бакенщика исчезнет полностью. Энергии как будто нет, а масса осталась. Как это согласовать с выводом об эквивалентности того и другого?

В предпоследней фразе — умышленная (с моей стороны) ошибка. Энергия у «остановленного» леденца не пропала. Потому что движение в нем не прекращено. Нет лишь механического перемещения леденца как целого тела. Зато есть (причем, относительно бакенщика!) беспрерывная тепловая пляска атомов и молекул (заморозьте леденец — и он станет легче; правда, совершенно неуловимо). Есть движение электронов в атомах и между ними, мезонов в атомных ядрах. Леденец (как и любое другое тело, будь то песчинка, пушинка, капля, гора, планета) лишь внешне спокоен. Внутри, в микромире своем, это клубок молниеносных вихрей, вибраций, сдвигов. И, конечно же, этот клокочущий круговорот материи, хоть он и невидим для глаз, неощутим для рук, — средоточие гигантской энергии, той самой, что эквивалентна «массе покоя» — массе «остановленного» леденца.

Хорошо. Это можно понять, когда речь идет о механической энергии. Или о тепловой, которую есть резон свести к механической. А как быть с энергией электрической, или магнитной, или химической? Все ли виды ее имеют массу и вес?

Все.

Листаем книжку назад, к странице 70. Вспоминаем закон сохранения энергии. Он утверждает: при превращениях энергии из одного вида в другой ее количество не может измениться — увеличиться или уменьшиться. Оно постоянно и неизменно. Следовательно, когда работает турбина, вертится ротор генератора и механическая энергия переходит в тепловую и электрическую, то вместе с нею переходит- масса. И в том же соотношении. Свою долю массы получает тепло, свою — электричество.

Значит, и электрическая энергия обладает массой, как и магнитная, и ядерная, и все остальные ее формы.

Итак, масса покоя соответствует огромной «энергии покоя». И Эйнштейн подсказал нам, как просто можно оценить ее количество. Поскольку энергия эквивалентна массе, измерить ее можно так же, как массу, — взвешиванием тела. А перевод единиц массы в единицы энергии надо сделать по формуле Е = mс² (Е — энергия в эргax, m — масса в граммах, с — скорость света в сантиметрах в секунду). Эта формула ныне стала самой известной из всех когда-либо выведенных физиками. Ее печатают даже на почтовых марках (я видел ее на марке африканского государства Ганы!).

А получена она была, кстати сказать, без всяких разговоров о внутреннем движении в веществе. Эйнштейн добыл ее из гораздо более общих соображений.

Скрытое за формулой

Эйнштейн, человек с добрым и тонким юмором, оставил нам коллекцию остроумных афоризмов. Среди них многозначительный парадокс: «Ни один ученый не мыслит формулами». Как понимать это?

Разумеется, умение легко оперировать в уме математическими абстракциями незаменимо. Без него не может жить современный физик-теоретик. Но за формулами он всегда чувствует нечто большее. В символике вычислений и решений он ищет откровения природы, которые могут выглядеть нелепыми, могут показаться математической фикцией, но на деле отражают глубинную сущность мира.

Яркий пример — открытие эквивалентности энергии и массы. Оно было подсказано неожиданным видом математического выражения кинетической энергии, которое Эйнштейн вывел из своей теории.

Вышло так. Строгими и последовательными этапами, с учетом относительности времени, расстояний, массы для кинетической энергии движущегося тела была получена формула:

K_p = mс² — Е₀,

где К —релятивистская кинетическая энергия,

m — релятивистская масса, равная

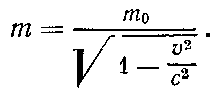
m_o — масса покоя, а Е_о — какая-то еще не известная нам постоянная величина. Попробуем ее определить.

В свое время (страница 66) мы согласились, что кинетическая энергия есть «обещание работы». Заставим наше Кр выполнить обещание - пусть поработает сколько сможет. Самое большее, что ей доступно, — отдать на работу всю себя целиком. Тогда она исчезнет, а тело полностью затормозится, его скорость станет равна нулю (v = 0). При этом будет: К_р =0, а mс² = m₀с²

(так как при v = 0

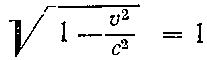
И, следовательно, 0 = m₀с² — Е_о, то есть Е_о = m₀с², а К_р = mс² — m₀с².

Последняя формула при малых скоростях переходит в классическую K_кл = m₀v²/2 — поверьте, что это так. Соответствующие не очень сложные выкладки я опускаю.

А основная черта несходства классической формулы с релятивистской — в математической структуре. Если К_кл—одночлен, то K_р — двучлен, разность двух однотипных выражений. Те, кто «мыслит формулами» (лучше сказать: только формулами), склонны не обратить внимания на этот факт, посчитать его случайностью. Но Эйнштейн за математическим своеобразием угадал сокровенный секрет природы: то, что любое вещество — это, по сути дела, титанической силы взрывчатка.

Пусть движущееся тело — разрывная пуля. Исполнить работу она «обещает», не только затормозившись до нулевой скорости, но и взорвавшись. Соответственно ее полный запас энергии равен сумме кинетической энергии и внутренней энергии возможного взрыва. А поэтому кинетическая энергия (К) представится разностью между полной (Т) и внутренней (Е) энергиями. Запишем это:

К = Т — Е.

Заметили аналогию с формулой К_р = mс² — m₀с²? Благодаря тому, что в тело внесена внутренняя энергия, для его кинетической энергии получен двучлен, весьма похожий на тот, что выведен Эйнштейном для кинетической энергии любого тела (а не только разрывной пули).

Значит, любое тело подобно разрывной пуле. Даже в покое оно заключает-таки в себе энергию. Причем фантастически огромную. Камень, капля воды, песчинка способны взорваться. И леденец. И космонавтки Алла и Элла. Впрочем, взрываться им совсем не обязательно. Отдать свою внутреннюю энергию они в принципе могут и спокойно. Если бы можно было сделать «леденец Эйнштейна», обсасывая который вы слизывали бы с него всю энергию-массу (каждый день — 3000 калорий), то он заменил бы вам пищу на сто тысяч лет!

Для нас с вами это не неожиданность. Но ценно то, что вывод обошелся без всяких допущений о внутренних движениях в веществе. Что бы ни происходило в недрах тела, раз уж масса его m граммов, то запас его внутренней энергии E = mс² эргов. Граммы массы надо дважды помножить на скорость света — так они переводятся в единицы энергии — эрги!