Глава 4. МОГУЩЕСТВО МЕХАНИКИ

Дорога в школу

Я думаю, древнегреческие школьники были ничуть не глупее современных пионеров, даже из числа отличников. И учителя у них были, быть может, неплохие. Вся разница в уровне знаний. Учителя помнили слова своих учителей, которые еще очень мало знали, еще не умели смотреть в глубь вещей.

Видя быстро летящее копье, заброшенное сильной рукой, хотелось сказать, что сила рождает скорость. Так и говорили, и учили, и заучивали. А это была ошибка, ибо сила дает не скорость, а ускорение.

Видя лист, падающий медленнее шишки, обобщили это на все тела и объявили, что тяжелое падает быстрее легкого, — снова ошибка.

Видя восходящее и плывущее по небосводу Солнце, уверовали, что оно кружится вокруг Земли. Так и записали в священных книгах, а потом, спустя века и тысячелетия, гнали в тюрьмы и на костер несогласных и прозорливых.

Ошибки громоздились друг на друга, сбивали с толку, путали мысли, вживались в сознание. Из этих ошибок, освященных религией, авторитетами, традициями, строилось представление о мире — очень наивное, неверное, непохожее на наше. С такой «моделью мира» было трудно искать истину даже людям умным и талантливым.

И все-таки от года к году, от века к веку копились крупицы истины. И вспыхивали открытия. Рождались, учились, поднимали головы гениальные первооткрыватели. Их мудрость — мудрость Коперника, Галилея — вырастала в стройную систему науки. Пробил час — и прозвучал голос Ньютона, подарившего человеку новое зрение — физику, охватившую весь необозримый мир.

Знание, в отличие от искусства, не бросается в глаза. Оно всегда неприметно, скрыто в скромных словах или сухих строках формул. Вероятно, поэтому на уроках физики мы редко удивляемся откровениям ньютоновских законов. И напрасно. В учении Ньютона все, с начала до конца, достойно удивленного восхищения.

Земля и яблоко

Классической механике подвластны разнообразнейшие силы. Тянут железо магниты, отталкиваются от дороги колеса автомобиля, ударяются, расходясь в стороны, бильярдные шары — все это неукоснительно подчиняется законам Ньютона.

Но раз уж мы в этой книжке размышляем о падающих телах, побеседуем поподробнее об одной только силе тяготения.

Я уже много говорил о ней, вездесущей и таинственной, вместе с вами доискался ее главной особенности — неизменной пропорциональности тяжелой массе тела, недоумевал по поводу ее странного «действия без прикосновения». Эта поразительная ее особенность остается для нас загадкой, которую на этих страницах еще рано пытаться разгадывать.

Но хоть мы не в состоянии объяснить, почему сила тяжести проникает через пустоту, нам пора задуматься над тем, как это происходит.

Сегодня всем известно: вдали от Земли тяжести нет. Это ясно каждому шестикласснику, это вошло в сознание из бесчисленных книжек, газетных статей, радиопередач. Во времена же Ньютона мир выглядел иным. О том, что сила тяжести не везде одинакова, лучшие умы могли только догадываться. Никаких опытов, свидетельствующих о ее уменьшении с высотой, не было. Наоборот, на башне и в подвале тяжелое ядро представлялось одинаково тяжелым.

И все-таки Ньютон, приглядевшись к перемещениям небесных тел, уверенно заявил: с увеличением расстояния от Земли тяготение убывает.

А как убывает? Быть может, на высоте облаков уже нет тяготения? Если верить упорной легенде, Ньютон ответил на это «как», созерцая в своем саду падающее яблоко. На самом деле, если и существовало это историческое яблоко, то, разумеется, не оно одно навело великого физика на его открытие. Были и другие, куда более существенные подсказки: замечательные идеи и вычисления Галилея, прозорливые слова Кеплера и математические закономерности, подмеченные им в движении планет, нескончаемые размышления самого Ньютона об инерции, массе, падении тел.

Догадка эта даже сегодня не может представиться легкой и естественной. Если она и проста, то наверняка гениальна. Сила тяготения F пропорциональна массам притягивающихся тел m1 и m2, но она убывает тем сильнее, чем больше становится квадрат расстояния между центрами притягивающихся масс r2. Именно квадрат! Не просто расстояние, не куб его, а квадрат. И именно между центрами масс. Дело происходит так, как если бы вся масса каждого тела была сосредоточена в бесконечно малом объеме — в точке, совпадающей с центром тяжести. Понять и обосновать это Ньютону стоило больших трудов.

Такова сущность замечательного ньютоновского открытия, которое вскоре стало знаменитым и получило название закона всемирного тяготения.

Вот формула:

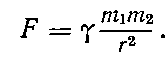
Символ ? означает «постоянную тяготения» — множитель пропорциональности, уравновешивающий обе части равенства. Физический его смысл прост — это сила притяжения двух тел массой по грамму, находящихся в сантиметре друг от друга. ? можно узнать из эксперимента: измерить эту силу, заставив притягиваться два шарика с массой по грамму, подвешенных рядом на тонких нитях в сантиметре друг от друга. В таком грубом опыте, правда, никакого измерения не получится — граммовые шарики притягиваются ничтожно слабо. Успех здесь принесен другим, более тонким опытом, выполненным английским физиком Кавендишем.

Всемирный закон на столе

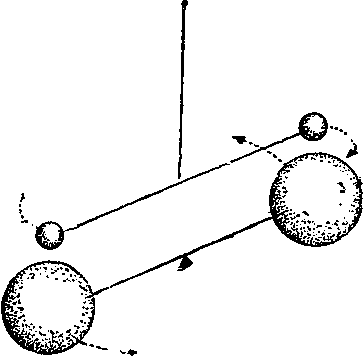
Кавендиш тонко задумал и исполнил свой эксперимент.

В тщательно откачанном стеклянном баллончике висит на тоненькой нити легкое коромысло со свинцовыми шариками на концах. Перед ними укреплены большие свинцовые шары. Таким образом, коромысло с маленькими шариками обладает незначительной массой (стало быть, и инерцией), а сила притяжения крупных шаров достаточно велика. В результате совместные усилия двух шаров чуть-чуть сдвигают коромысло. Маленькие шарики с еле заметным ускорением «падают» на большие. Нить слегка закручивается. Но на ней подвешено легонькое зеркальце, отражающее световой луч. Где-то далеко, на стене лаборатории, укреплен экран с делениями, по которому скользит световой зайчик от луча, отраженного зеркальцем. И поэтому почти неуловимое закручивание нити заставляет световой зайчик перемещаться по экрану.

Так закон всемирного тяготения был впервые проверен в лаборатории. По смещению светового зайчика Кавендиш рассчитывал силу притяжения шариков. Меняя их массы, ученый доказал справедливость того, что записано в числителе формулы закона тяготения: пропорциональность силы обеим тяготеющим массам. А варьируя расстояние между шарами, он подтвердил обратную пропорциональность силы притяжения именно квадрату расстояния. Но главное, что он узнал, — это значение постоянной ?. Ведь и массы, и силы, и расстояния были измерены — осталось вычислить постоянную тяготения.

Она оказалась равной 6,7·10^-8см³/(г·сек²)

Дальше следует феерический фонтан волшебства ньютоновской механики.

Взвешиваем планету

Что бы такое взвесить поудивительнее? Хотите Землю? Пожалуйста! К вашим услугам формула всемирного тяготения. Вместо Земли можете положить на весы яблоко. Получилось сто граммов. Это масса яблока m_я. На весах и гирях всегда проставлены именно единицы массы.

Чтобы получить силу тяготения F, вспоминаем второй закон Ньютона и массу яблока множим на земное ускорение g, то есть 100 г·981 см/сек². Это вес. Рискуя показаться навязчивым, я напомню, что когда-то мы определяли его как давление тела на опору, потом — как силу тяготения, исходящую от центра масс Земли и приложенную к телу. Разумеется, яблоко, притягиваемое Землей, давит на опору. В свою очередь, опора давит на яблоко — исполняется третий закон. А потому между яблоком и опорой мы вправе поместить пружину. Она сожмется тем сильнее, чем сильнее тяготение. Вот мы и измерили с помощью весов земное притяжение.

Знаете радиус Земли? Напомню — 6300 километров, или 6,3·10⁸ см (перед вычислением все величины нужно свести к одной системе единиц).

Теперь можно вычислить.

Масса Земли m_з=Fr²/(?·m_я) = 100г · 981 см/сек² · (6,3·10⁸ см)² /(6,7·10^-8 см³/(г·сек²) ·100 г) = 6·10²⁷ г = 6·10²¹ т.

Подсчитали? Загляните в энциклопедию — масса Земли именно такова.

Вот и свершилось волшебство — по весу яблока определена гигантская масса планеты.

Это вас не восхищает?

Без весов

Пожалуй, будет лучше, если внимательный читатель вместо восхищения поймает автора за рукав и сделает ему замечание: по формуле закона всемирного тяготения массу Земли можно было определить и без взвешивания яблока. Ведь если вес яблока F = m_яg, а r — земной радиус, то масса Земли

m_з = m_яgr²/(?m_я) = gr²/?

Масса яблока в числителе и знаменателе сокращается. Формула открывает удивительную возможность взвешивать Землю вообще без всяких весов — по постоянной тяготения и величине ускорения силы тяжести.

Если вы забыли значение g, покараульте с секундомером в руках возле какой-нибудь яблони, засеките время, за которое очередное яблоко пролетело с ветки до земной поверхности, потом измерьте высоту ветки, по галилеевской формуле s=gt²/2 (из первой главы этой книжки), подсчитайте g и вставьте в только что выведенную формулу m_з= gr²/?. Через минуту вычислений вы узнаете, во всей ее огромности, земную массу. Узнаете количество вещества своей планеты! Недаром Кавендиш, который, разумеется, превосходно помнил значение g, назвал свой исторический эксперимент, позволивший впервые вычислить постоянную тяготения «взвешиванием Земли». Он узнал ? и сразу подсчитал, какова масса земного шара.

Этим уже стоит чистосердечно восхититься.

Да, падающее яблоко многое могло подсказать наблюдательному Ньютону.

На вышине

Догадываетесь, в чем секрет замечательного умения, которым вы овладели вслед за Ньютоном и Кавендишем? Секрет в том, что использовано равенство тяжелой и инертной масс: ведь в числителе формулы стояла инертная масса из второго закона Ньютона, а в знаменателе — тяжелая масса из закона всемирного тяготения. Мы их сократили и были вправе сделать это только потому, что они не в состоянии «переспорить» друг друга, или, иначе говоря, только потому, что все тела падают одинаково быстро.

Так из явлений маленьких, ежеминутно происходящих на наших глазах, вырастают закономерности широчайшего охвата. Не в отвлеченном рассуждении, не в расплывчатой фразе, а в конкретном деловом расчете физик совмещает песчинку с планетой.

Предсказания Ньютона широки и многообразны.

Вы хотите узнать, сколько будет весить килограммовая буханка хлеба на вершине Монблана? Пожалуйста, используйте формулу всемирного тяготения. Получится 997 граммов. Пожелали выяснить значение ускорения силы тяжести на высоте орбитального полета Гагарина — та же формула даст вам ответ. Проделайте вычисления, и вы убедитесь, что оно там уменьшится незначительно — всего на одну шестнадцатую часть. На столько же уменьшился бы и вес. Это неожиданно для наивных людей, полагавших, что спутники невесомы из-за удаления от земного шара.

Боюсь, самым любопытным из читателей уже захотелось взвесить Солнце.

А почему бы и не взвесить?

Взвешиваем Солнце

Это весьма просто. Расстояние до Солнца спросим у астрономов. Они скажут: 150 000 000 километров. Кроме того, мы знаем, что Земля падает на Солнце, хоть и не может упасть.

Об этом странном факте нелишне поговорить поподробнее, пользуясь законами Ньютона.

Благодаря своей инерции Земля постоянно стремится улететь от Солнца по прямой (первый закон Ньютона). Вместе с тем Земля испытывает солнечное притяжение (закон всемирного тяготения) и приобретает ускорение, направленное к Солнцу (второй закон Ньютона). Эти два движения складываются — получается вечное обращение Земли вокруг Солнца.

Стоит напомнить, что свободное падение отнюдь не обязано быть отвесным. Пуля, вылетевшая из дула пистолета параллельно земной поверхности, приближается к ней так же быстро, как и пуговица, упавшая со стола. Земля как пуля. Она не отвесно падает на Солнце.

Каково же ускорение падающей Земли?

Длину земной орбиты подсчитать проще простого. Эта орбита — круг радиусом 150 миллионов километров. Помножьте радиус на «два пи» (6,28) — выйдет миллиард километров. Время — 365 суток, год нашей жизни. Отсюда нетрудно подсчитать, что за секунду Земля успевает пролететь 30 километров по своей орбите и одновременно упасть к Солнцу на три миллиметра. По формуле Галилея S =a_ct²/2 сразу же получаем значение ускорения Земли к Солнцу: а_с = 0,6 см/сек². Маловато, конечно. Но зато мы можем не опасаться катастрофического столкновения со своим жарким светилом.

Масса Солнца теперь выясняется автоматически: 2·10²⁷тонн. Обратите внимание, на этот раз нам не понадобилась масса Земли. Достаточно было знать ускорение ее падения на Солнце. Любое тело, находящееся на земной орбите, будет падать к Солнцу с тем же ускорением — 0,6 см/сек². Так в астрономическом масштабе продолжает действовать постоянство ускорения свободного падения для тел каких угодно масс. Явление, которое мы подметили на сосульках, падающих с карниза!

Ангелы-бездельники

От Солнца переходим к планетам.

Было время, когда неглупые люди всерьез полагали, что планеты все время подталкиваются ангелами, потому-де они и движутся. На каждую по ангелу.

Как следует из ньютоновских законов, ангелы эти — бездельники. Планеты великолепно обходятся без них: по инерции летят прямо, а влекомые солнечным тяготением, падают на светило. В результате сложения этих двух движений планеты сворачивают с прямого пути и движутся по эллипсам — так называют в геометрии фигуры, похожие на овал.

Сумма расстояний точек эллипса от двух точек, лежащих внутри фигуры и называемых фокусами, постоянна (это геометрическое определение).

В одном из фокусов всегда находится Солнце. Это знал еще Кеплер. Если же фокусы совпадают, получается круг. Многие планеты (в их числе наша Земля) движутся по почти точным кругам.

Ньютон разработал тонкий математический метод для вычисления планетных путей и решил с его помощью массу трудных задач.

Удалось найти зависимость периодов обращения двух разных планет (длительность «годов») от близости планет к Солнцу. Кубы наибольших расстояний планет, на которых они оказываются в своем движении вокруг Солнца, пропорциональны квадратам их «лет». И эта особенность, гениально угаданная Кеплером, нашла подтверждение в строго обоснованной теории Ньютона, который, однако, внес уточнение — зависимость от масс планет.

В разных местах эллипса движение неодинаковое: с приближением к Солнцу оно ускоряется, с удалением от Солнца — замедляется. Как меняется скорость, подметил тот же Кеплер (радиус, проведенный от планеты к Солнцу, в равные промежутки времени «выметает» одинаковые площади). А Ньютон дал доказательство.

В конце концов удалось составить подробнейшее «небесное расписание» движения планет. И — ни одного ангела! Или, как заметил один физик, должность ангела занимает само Солнце.

Всеобщее послушание

Расписание исполнялось с отменной точностью. Планеты следовали по орбитам с предсказанной скоростью, их уверенно находили в предсказанных местах неба. В назначенные часы, минуты и секунды происходили восходы, заходы, противостояния, затмения Солнца и Луны. Солнечная система голосовала за механику Ньютона, за всемирное тяготение.

Единственное исключение — одна малая особенность в движении Меркурия, не уложившаяся в предсказания ньютоновской небесной механики. Об этом пойдет речь далеко впереди.

А как обстояло дело за пределами Солнечной системы? Послушны ли Ньютону звезды?

Да, послушны. Этот ответ был получен наукой уже после смерти великого физика, когда развилась звездная астрономия.

Особенно красноречивы многолетние наблюдения так называемых двойных звезд, тех, что находятся по соседству и медленно кружатся одна вокруг другой. Есть убедительный документ, свидетельствующий о том, что этот звездный вальс точно следует ньютоновскому закону — фотографии взаимного расположения звездной пары Сириус А — Сириус В, сделанные на протяжении одного почти полного оборота этой пары — с 1862 до 1904 года. Чертеж орбиты Сириуса В — это типичный эллипс. И звезда путешествует по нему именно так, как назначено ньютоновской небесной механикой: чем дальше от Сириуса А, тем медленнее движется Сириус В. Возле фокуса он за шесть лет успевает пробежать такое же расстояние, какое вдали от фокуса преодолевает за шестнадцать. Это как раз и требует теория тяготения!

Шагнем дальше в ширь Вселенной. Слушаются ли Ньютона целые звездные города?

В нашей Галактике ученые отыскали изумительно красивые звездные рои — шаровые скопления. Чем ближе к центру скопления, тем больше звезд. Но даже в глубоких недрах его, где на фотографии получается сплошной белый фон, звезды настолько далеки друг от друга, что сталкиваться не могут. Они всегда действуют друг на друга только тяготением. Поэтому скопления и круглы — центральные области притягивают периферийные. Та же причина сделала шарами нашу Землю, Солнце и все планеты.

Даже в галактиках — необозримых скопищах звезд и звездных систем — астрономы находят явные следы мощного тяготения. Оно действует даже в фантастически гигантских скоплениях галактик, пронизывает всю Вселенную.

На кончике гусиного пера

Самый яркий эпизод торжества идей Ньютона относится к первой половине прошлого века.

Тогдашние астрономы никак не могли втиснуть в рамки ньютоновской теории движение Урана, недавно открытой и самой дальней из известных в ту пору планет. Уран двигался, в общем, так, как требовало «расписание», но в тонкостях нашлись непонятные отклонения. Планета немножко выходила из назначенного курса, слегка искривляла эллипс своей орбиты. Чтобы объяснить эти особенности, астрономы учли в расчетах не только солнечное притяжение, но и тяготение соседних с Ураном планет-гигантов Юпитера и Сатурна. Тем не менее все странности поведения Урана не удалось объяснить. Значит, Ньютон не прав? Его механика в чем-то грешит?

Положение сложилось драматическое.

И вот двое ученых — англичанин Адаме и француз Леверье — независимо друг от друга сделали предположение, которое витало в воздухе и напрашивалось само собой: а нет ли за Ураном еще одной планеты — очень далекой, слабо светящейся и потому еще не замеченной?

Опять заскрипели перья, выписывающие уравнения небесной механики.

Теперь их спрашивали: где искать неведомую планету, вызвавшую возмущения в движении Урана? Уравнения дали свой математический ответ: в такие-то моменты времени загадочная планета должна находиться в таких-то местах неба.

Леверье и Адаме послали расчеты в несколько обсерваторий. И когда астрономы-наблюдатели направили телескопы так, как посоветовали их корреспонденты- теоретики, планета действительно нашлась. Маленькая, едва заметная. Ей дали имя Нептун. И отпраздновали знаменательную победу теории тяготения. Это было в 1846 году.

Спустя 84 года при таких же примерно обстоятельствах американцу Томбо удалось открыть самую далекую из наших планет — Плутон.

На кончике авторучки

Совсем недавно, в 1964 году, произошло еще одно удивительное событие. Уравнения небесной механики помогли американскому астроному Ван де Кампу понять причину ничтожных колебаний Летящей звезды Барнарда — одной из ближайших к нам звезд, названной так за свое быстрое движение.

Казалось бы, раз где-то в космосе летит звезда, так уж пусть она летит по инерции прямо — как велено первым законом Ньютона. А она «болтается». Правда, чуть-чуть — за год на десять угловых секунд, самое большее. Но и этого достаточно, чтобы взяться за вычисления.

Подробная расшифровка колебаний привела к замечательному и долгожданному успеху: впервые с полной достоверностью было доказано существование планеты, вращающейся вокруг далекой звезды. Эта планета, действуя своим тяготением на звезду, заставляет ее мчаться не по прямому, а по слегка волнистому пути.

Ван де Камп выведал немало подробностей о невидимом спутнике звезды Барнарда. Он весьма массивен — в полтора раза тяжелее нашего Юпитера (а Юпитер в 318 раз тяжелее Земли). Путь спутника — довольно вытянутый эллипс. Самое большое расстояние его от звезды Барнарда — 660 миллионов километров. Год — в 24 раза дольше нашего.

Анкета, как видите, получилась довольно полная.

И все это сказано про небесное тело, которое никто никогда не видел и, быть может, не увидит. Такова проницательность науки. Той самой науки, которая началась с опытов Галилея, бросавшего ядра и пули с Пизанской башни. Ведь спутник звезды Барнарда тоже «падает», и по тем же законам!

Впрочем, тут особенно ясно, что и звезда падает — это ее падение ведь и выдало таинственного спутника, показало, что она не одинока. Так и должно быть: звезда тянет спутник, который, в свою очередь, тянет звезду. Действие равно противодействию.

Не видя Луны

Есть анекдот. На экзамене профессор спрашивает студента:

Вы видели Луну?

Нет! — поспешно отвечает студент, мечтающий избавить себя от новых вопросов.

Но даже если бы хитрый студент и в самом деле ни разу в жизни не поднял глаз на Луну, все равно он мог бы немало узнать о ней. По той же самой причине, по которой Ван де Камп открыл и описал невидимый спутник звезды Барнарда.

Важно то, что падает не только Луна, но и Земля. Обе они, влекомые тяготением, стремятся к общему центру масс.

Какие же события вызываются на Земле ее падением на Луну? Очень заметные и существенные. Прежде всего приливы и отливы.

На вопрос: «Почему бывают приливы и отливы?» — часто отвечают: «Очень просто, воду океана притягивает Луна». Считают так: под Луной на океанской поверхности вырастает огромный водяной горб, а так как Земля под Луной вращается, то горб этот перемещается, дабы все время оставаться «подлунным», и набегает в конце концов на берег. Согласны?

Ответ неверен. Если бы дело происходило так, то приливы и отливы наступали бы всего один раз в сутки. А они бывают дважды в сутки.

На самом деле водяных горбов на поверхности Мирового океана два — первый действительно под Луной, а второй в диаметрально противоположной стороне. И вершина второго направлена от Луны. Оба горба сохраняют свое положение в пространстве, а Земля кружится, вот и выходит, что приливная волна дважды в сутки заливает берега.

Но почему же все-таки горбов два, а не один? И почему второй словно бы отталкивается от Луны?

Никакого отталкивания нет. Причина этого явления в том-то и состоит, что Земля вместе с Мировым океаном непрерывно падает в сторону Луны, хоть и не может «упасть», так же как и Луна не может упасть на Землю. Прямо под Луной лунное притяжение сильнее (потому что там океан ближе к Луне) и, значит, больше ускорение падения. «Подлунный» горб падает быстро. А с обратной стороны Земли океан на двенадцать тысяч километров дальше от Луны, там ее тяготение слабее, и вода отстает в падении.

Здесь я задам вам проверочный вопрос (из числа довольно трудных — на нем иногда проваливаются даже студенты-физики).

Кроме лунных, по океану бежит еще пара приливных горбов, рожденных притяжением Солнца. Они гораздо меньше, чем лунные. Почему?

Вертится на языке фраза: потому, что Солнце притягивает воду океанов слабее, чем Луна. Так и говорят иные незадачливые студенты на экзаменах, огорчая терпеливых экзаменаторов, ибо ответ этот грубо ошибочен. Солнце влечет к себе Землю (и все, что на ней есть, в том

числе и океаны) неизмеримо сильнее, чем Луна. Ведь не вокруг Луны, а именно вокруг Солнца обращается наша планета.

А невелики солнечные приливные волны на Земле потому, что наше светило очень уж далеко — в 150 миллионах километров. В пять с лишним тысяч раз дальше, чем Луна.

Это значит, что земной диаметр по сравнению с расстоянием до Солнца ничтожно мал. Следовательно, весьма незначительна и разница в силе солнечного тяготения по ту и другую сторону нашей планеты. Другими словами, на дневной и ночной сторонах Земли вода океана падает к Солнцу с очень близкими ускорениями. Поэтому и невелики солнечные горбы.

Все дело, как видите, в том, что по сравнению с расстоянием Земля — Луна наша планета довольно велика, а по сравнению с расстоянием Земля — Солнце мала. Для солнечного тяготения Земля — точка, для лунного — отнюдь не точка. Вот и ответ на хитрый экзаменационный вопрос.

Вообще, подробная картина приливов получается довольно сложной и запутанной. Но для понимания ее не требуется ничего, кроме знания ньютоновской механики, теории тяготения и, конечно, карты береговой линии материков.

Есть, кстати сказать, и приливы суши, потому что земная кора не абсолютно тверда.