Дискретный набор энергетических уровней
Существует дискретный набор энергетических уровней для данных значений массы m и размера ящика L. Поскольку квантовое число n принимает значения 1, 2, 3 и т. д., соответствующие значения энергии будут равны
h2/8?m?L2, 4?h2/8?m?L2, 9?h2/8?m?L2, и т. д.
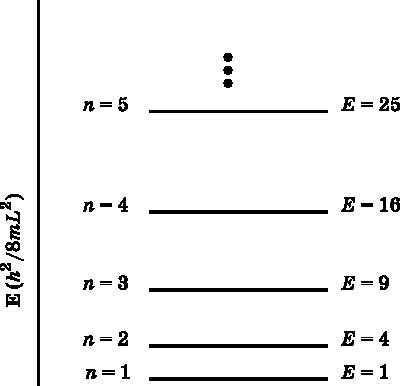
Рис. 8.6.Энергетические уровни частицы в ящике. Здесь n — квантовое число, а E — энергия, которая увеличивается как квадрат квантового числа. Энергия выражена в единицах h2/8?m?L2, так что хорошо видно, как она возрастает. Штриховой линией обозначена нулевая энергия. Самый низкий энергетический уровень не совпадает с линией E=0 в отличие от случая классической частицы в ящике
На рис. 8.6 представлена диаграмма энергетических уровней для первых нескольких значений энергии частицы в ящике. Энергия выражена в единицах h2/8?m?L2. Чтобы получить фактическое значение энергии, нужно просто подставить конкретные значения m и L в формулу для энергетических уровней. На диаграмме видно, что энергия увеличивается как квадрат квантового числа n. Штриховой линией обозначено, где энергия равна нулю. Квантовая частица в ящике на наинизшем энергетическом уровне имеет ненулевую энергию, чем резко отличается от классической частицы в ящике. На классической ракетбольной площадке энергия, которой может обладать мяч, непрерывна. Ударяя по мячу чуть сильнее или чуть слабее, его энергию можно увеличить или уменьшить на любую величину. Однако в квантовом ракетболе возможны лишь отдельные значения энергии, показанные на рис. 8.6. Как отмечалось в начале нашего разговора о квантовой частице в ящике, наименьшая энергия не равна нулю. Если бы квантовая частица в ящике могла иметь нулевую энергию, это нарушало бы принцип неопределённости.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК