ИСТОРИЯ ОТКРЫТИЯ ЗАКОНОВ УДАРА
ИСТОРИЯ ОТКРЫТИЯ ЗАКОНОВ УДАРА
Вопросами теории удара интересовался уже Галилей. Им посвящен «шестой день» знаменитых «Бесед», оставшийся не вполне законченным[23]. Галилей считал нужным определить прежде всего, «какое влияние на результат удара оказывают, с одной стороны, вес молота, а с другой — большая или меньшая скорость его движения, и найти, если возможно, способ измерения и выражения того и другого вида энергии»{99}.
При решении этих вопросов Галилей полагал необходимым начать с экспериментов. Но если при экспериментальном исследовании законов падения тел он уже имел в качестве ориентира теоретически выведенную формулу униформно-дифформного движения, то здесь, в теории удара, приходилось начинать заново.
Неизвестно, сколько и какие именно эксперименты произвел Галилей. Нет сомнения, что описываемый ниже опыт был им действительно произведен. Однако он разочаровал Галилея. Опыт заключался в следующем. К коромыслу весов были подвешены на одном конце противовес, а на другом два сосуда: первый с водой, а второй, подвешенный под первым на расстоянии двух локтей, пустой. Верхний сосуд имел отверстие, которое можно было закрывать и открывать.

ГАЛИЛЕО ГАЛИЛЕЙ (1564-1642)
Итальянский астроном, механик и физик, один из основоположников точного естествознания. Он открыл закон инерции, законы падения тела, колебаний маятника. С помощью изготовленной им зрительной трубы Галилей впервые наблюдал небесные светила. Открыл горы на Луне, четыре спутника Юпитера, фазы Венеры, звездное строение Млечного Пути, пятна на Солнце
Галилей предполагал, что при вытекании воды сила удара заставит опуститься плечо коромысла, и величину этой силы можно будет измерить посредством добавочного груза на другом плече. Результат оказался «неожиданным, даже совершенно изумительным»: «Как только отверстие было открыто и вода начала вытекать, весы наклонились, но в сторону противовеса; когда же вытекающая вода достигла дна нижнего сосуда, дальнейшее опускание противовеса прекратилось и он начал равномерно подниматься, пока не достиг прежнего положения и весы не пришли снова в равновесие, не отклонившись и на волос в другую сторону».
Для нас теперь в этом нет ничего удивительного.
До того как первая капля достигнет нижнего сосуда и будет производить давление на его дно, имеет место уменьшение давления в результате того, что исключается вес струи жидкости и, кроме того, сказываемся направленная вверх реакция вытекающей струи. Такова причина того начального отклонения стрелки, которое заметил Галилей. Когда вытекающая струя достигнет нижнего сосуда, давление на дно компенсирует потерю давления, происходящую в результате указанных причин.
Сам Галилей объяснил это явление тем, что «вся вода, содержащаяся в струе, как бы снята с весов»; пока вода вытекает, действует лишь удар, который соответствует скорости, приобретенной при падении с высоту двух локтей. Однако полная, уточненная количественно картина явления осталась ему неизвестной.
Вот почему Галилей счел себя вынужденным избрать другой путь и обратиться к опыту забивки свай. Но характерно, что здесь, прежде чем экспериментировать, он стал обстоятельно, во всех деталях обдумывать, что же могут дать подобные эксперименты, какие привходящие условия могут нарушить точность их показаний. Иначе говоря, вместо того чтобы производить опыты вслепую, Галилей сначала стал, экспериментировать мысленно. Из самого его изложения видно, что для примера были взяты произвольные величины.
Итак, в землю забивают сваю. Вес бабы — 100 фунтов, высота — 4 локтя, глубина, на которую свая входит в землю, — 4 дюйма. Предположим, что для достижения того же результата без удара, путем одного лишь давления «мертвого груза», требуется 1000 фунтов. Исходя из этих условных данных, Галилей вскрывает все возможные трудности эксперимента. Если при каждом новом ударе сопротивление грунта возрастает то ли от его изменения с глубиной, то ли от уплотнения самого грунта при ударе, становится трудным сравнение силы удара и того, что Галилей называл давлением «мертвого груза». Вот почему он пришел к выводу, что нужно начинать с рассмотрения случаев, когда «тело, испытывающее удар, оказывает последнему всегда одно и то же сопротивление».
Однако и новый эксперимент с двумя грузами, соединенными между собой перекинутой через блок нитью, имел свои трудности.
Шестой день «Бесед» остался, как уже сказано, не вполне законченным и обработанным. Вывод, к которому пришел Галилей, в значительной мере неопределенный и предварительный: сила удара имеет бесконечно большой момент, ибо не существует такого большого сопротивления, которое не могло бы быть преодолено силой даже самого незначительного удара. Однако указание на то, что энергия удара слагается из скорости и веса, что удар слагается из элементарных импульсов и что эффект давления мертвого груза отличен от эффекта удара, весьма важно.
На аналогичные трудности сравнения действия мертвого груза и удара указывал Декарт (напомним, что ему не мог быть известен «шестой день» галилеевских «Бесед»). Декарт писал: «Сравнивать силу пресса с силой удара можно только по их эффектам: ибо пресс может действовать всегда ровно на протяжении долгого времени, тогда как сила удара продолжается весьма мало и никогда не бывает одинаковой на протяжении двух моментов подряд»{100}.
Излагая в «Началах философии» законы (или, как он называл их, правила) удара, Декарт заканчивает следующим заявлением: «Все эти доказательства настолько достоверны, что хотя бы опыт и показал обратное, однако мы вынуждены придавать нашему разуму больше веры, нежели нашим чувствам»{101}.
Это отнюдь не значит, что Декарт игнорировал опыт. Подобно Галилею, он пытался сначала осознать и осмыслить данные опыты, и, подобно Галилею, он быстро убедился во всей сложности такой задачи.
Поучительны в этом отношении письма Декарта к Мерсенну, относящиеся к первой половине 1640 г., т. е. написанные четырьмя годами раньше, чем только что цитированные «Начала философии».
Декарт рассуждал здесь, например, о том, как при помощи молотка лучше сплющивать пулю — на мягкой подушке или на твердой наковальне? «Удивляюсь, — писал он, — как вы еще не слыхали, что лучше можно сплющить свинцовую пулю молотком на подушке и на подвешенной наковальне, подающейся под ударом, чем на наковальне, стоящей прочно и неподвижно; ведь этот опыт общеизвестный. И в механике есть бесконечное множество подобных явлений, зависящих от одной и той же причины, а именно: чтобы расплющить свинцовую пулю, недостаточно ударять по ней с большой силой, но нужно также, чтобы эта сила длилась некоторое время, чтобы части этой пули имели время переменить свои положения. Так вот, когда эта пуля положена на неподвижную наковальню, молоток отскакивает кверху почти в то же мгновение, когда он ударил, а потому не имеет достаточно времени расплющить пулю, между тем как в случае, если наковальня или другое тело, поддерживающее эту пулю, уступают удару, это приводит к тому, что молоток дольше прилегает к ней»{102}.
В другом письме Декарт вернулся к деталям тех же операций. «Нужно пользоваться молотком не слишком крупным, потому что если бы он имел достаточную силу, чтобы совершенно расплющить пулю на наковальне, он не мог бы сделать большего на подушке. Кроме того, нужно поместить железную пластинку или какое-нибудь другое тело между пулей и подушкой, дабы она уходила при ударе вглубь настолько, что молоток терял бы свою силу, уходя в подушку». «Но есть и другой, более общеизвестный опыт, сводящийся к тому же принципу, — добавлял Декарт. — Все парижские повара вас уверят, что, когда требуется разрубить кость бараньей ноги, они кладут ее только на свою руку или на салфетку и, ударяя сверху, легче разрубают ее, чем на столе или наковальне».
И, как бы откликаясь на вопрос Галилея, Декарт заявлял о трудностях сравнения давления с ударом. «Я не могу сказать, сколько тяжести требуется, чтобы сравняться с ударом молотком; ибо это вопрос факта, где рассуждение не ведет ни к чему без опыта»{103}. Какой контраст с последующим заявлением в «Началах»!
Впрочем, опыты сталкиваются с множеством трудностей. «Все части молотка или другого ударного инструмента действуют одновременно, а не так, как солдаты, стреляющие один за другим. Однако для расплющивания пули требуется время, которое нужно для того, чтобы части этой пули успели переменить свое расположение, а это они не могут сделать мгновенно; и в зависимости от того, требуют ли части тел большего или меньшего времени для перемены положения под воздействием удара, можно по ним более эффективно ударять на подушке или наковальне деревяшкой, дубинкой или железным молотком и т. п. Стало быть, эти соотношения варьируют бесконечно».
Или еще категоричнее и разочарованнее в том же самом письме: «Кто смог бы произвести точный эксперимент, определив, какой груз и какой удар производят тот же эффект? Тогда можно было бы узнать, с какой скоростью он начинает двигаться при своем движении вниз. Однако я думаю, что такой эксперимент невозможно даже вообразить». О том же тремя месяцами позже Декарт писал тому же Мерсенну: «Я не вникаю здесь, каким образом можно подсчитать, сколько ударов маленького молотка потребовалось бы для того, чтобы сравниться с силой большого, так как при подобных подсчетах нужно принимать во внимание множество обстоятельств, и притом эти подсчеты трудно приводятся в согласие с опытом и приносят мало пользы; вот почему, думается мне, лучше об этом вообще не говорить».
Нельзя браться за выяснение законов удара путем экспериментирования наугад, без предварительного размышления и без ориентирующей абстрактной схемы.
Такую схему Декарт попытался дать в «Началах». Формулированные им законы неверны. Он не проводит различия между телами упругими и неупругими. Он не принимает во внимание направление скорости, рассматривает скорость как скалярную, а не векторную величину. От одного случая нет логически оправданного, непрерывного перехода к другому. Все это так. Но немаловажно выяснить, почему Декарт сделал именно эти ошибки. Ответ на такой вопрос позволит прояснить исходные кардинальные понятия его механики. -
В предыдущем разделе была речь о первых двух законах, которые Декарт считал основными. Третий закон, имеющий непосредственное отношение к сохранению количества движения и законам удара, состоит из двух частей.
Первая его часть гласит: «Если движущееся тело при встрече с другим телом обладает для продолжения движения по прямой меньшей силой, чем второе тело для сопротивления первому, то оно теряет направление, не утрачивая ничего в своем движении». В данном случае Декарт ссылается на опыт: «Твердое тело, будучи брошено и ударившись о более твердое и плотное тело, отскакивает в том направлении, откуда шло, но не теряет ничего в своем движении; наоборот, встречая на пути мягкое тело, тотчас останавливается, так как передает последнему свое движение».
Кроме того, Декарт ссылается на то, что это сопротивление второго тела есть причина, заставляющая первое тело изменить направление движения, однако нет никаких оснований, по Декарту, чтобы это сопротивление было причиной утраты движения: «Причина, заставившая его утратить направление, очевидна, именно — сопротивление тела, препятствующего ему следовать далее; отсюда, однако, для него нет необходимости терять что-либо в своем движении, тем более, что оно у него никогда не отнимается этим телом или какой-либо иной причиной и что движение движению не противоположно»{104}.
Во второй части третьего закона читаем: «Если же движущееся тело имеет большую силу, то движет за собой встречное тело и теряет в своем движении столько, сколько сообщает второму телу». Эту часть закона (т. е. сохранение количества движения при передаче его от одного тела к другому) Декарт в сущности ничем не обосновывает, кроме ссылки на «неизменность действия бога»{105}.
Обратимся теперь к более детальному разбору семи правил удара, сформулированных Декартом. Они относятся к идеальным неупругим, или, как говорит Декарт, твердым, телам, однородным по веществу, рассматриваемым вне соотношения с другими телами, а потому лишенным таких свойств, как тяжесть, порождаемая движением среды. Во внимание принимаются лишь величины тел, скорость их движения, а также сила инерции (т. е. сила, или способность «пребывать в покое и, стало быть, противостоять всему, что могло бы изменить его», и сила продолжать свое движение с той же скоростью и в том же направлении), сила, пропорциональная величине тела и скорости движения{106}.[24] Напоминаем, что в применяемых нами дальше обозначениях m1 и m2 у самого Декарта имеется в виду не масса (четкого понятия которой у него еще не было), а величина тела: Декарт всюду говорит о большем и меньшем теле, равных телах и т. п. Напомним также, что сохранение количества движения для Декарта — исходная аксиома, причем разница алгебраических знаков во внимание не принимается.
Следовательно, анализ семи «правил» (или различных случаев) удара основывается на требовании, чтобы до и после удара сумма количества движения оставалась постоянной:
m1u1 + m2u2 = m1v1 + m2v2.
Из возможных случаев Декарт выбирал такой, при котором перемена в состоянии столкнувшихся тел представлялась ему наименьшей.
Для уяснения всего сказанного важны соображения Декарта, возникшие уже после выхода в свет «Начал философии», а именно в 1645 г. Декарт хотел разъяснить здесь ход мысли, который привел его к ошибочному положению, будто меньшее тело неспособно сообщить движение большому, какова бы ни была скорость этого меньшего.
Декарт писал, что основание, которое заставляет его утверждать, что тело без движения никогда не может быть приведено в движение меньшим телом, с какой бы скоростью это меньшее ни двигалось, заключается в том, что таков закон природы: тело, приводящее в движение другое тело, должно иметь больше силы его двигать, чем это последнее ему сопротивляться. Но этот перевес может зависеть лишь от величины тела, ибо тело без движения имеет столько градусов сопротивления, сколько другое тело имеет градусов скорости. Причина заключается в том, что если такое тело, находящееся в покое, приводится в движение телом, обладающим вдвое большей скоростью, чем прежнее, оно должно получить вдвое больше движения, а такому вдвое большему количеству движение оно сопротивляется вдвое сильнее.
Далее Декарт утверждает в общей форме, что перемена в состоянии должна быть наименьшей: «Если два тела встречаются и их состояния несовместимы, должна произойти перемена в этих состояниях, делающая их совместимыми, и перемена эта должна быть наименьшей, иначе говоря, если определенная мера изменения этих состояний достаточна, чтобы они стали совместимыми, то не произойдет изменения в большей мере, чем она. При этом нужно принимать во внимание в движении два различных состояния: во-первых, движение само по себе, т. е. скорость, и, во-вторых, направленность этого движения в определенную сторону, каковые состояния изменяются одинаково трудно»{107}.
Уже в 1652 г., через восемь лет после выхода «Начал философии» Декарта, 23-летний Гюйгенс высказал свои первые сомнения в правильности законов Декарта, за исключением первого закона, который он признал верным (для упругих тел). Двумя годами позже в письме к ван Скоутену, который ему не советовал тягаться с Декартом, Гюйгенс сознавался, что ему самому было неприятно убедиться в ошибках Декарта. Еще двумя годами позже Гюйгенс написал свой первый трактат «Об ударе тел», не собираясь, однако, публиковать его.
В октябре 1666 г. Лондонское королевское общество объявило конкурс на решение задачи об ударе тел, на который представили свои работы Валлис, Рен и Гюйгенс.
Мемуар Валлиса был доложен 26 ноября 1668 г. Валлис разбирает случаи соударения неупругих тел. Рассматривая «силу» как пропорциональную произведению веса (т) и скорости (v), он дает для скорости и после удара соотношение
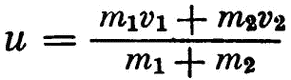
при движении обоих тел в одну сторону и
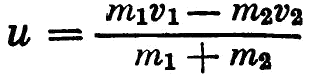
при встречном ударе.
Таким образом, в отличие от Декарта Валлис принял во внимание знаки плюс и минус, стоящие перед количествами движения (mv). При косом ударе Валлис вводит отношение радиуса к секансу угла. Сравнивая удар неупругих тел с ударом упругих, он ограничивается качественной констатацией наличия «восстанавливающей силы» в упругих телах.
Несколько позже, 17 декабря 1668 г., был представлен мемуар знаменитого архитектора Рена. Он подводил итог многочисленным экспериментам над упругими телами, которые Рен произвел совместно с математиком Гуком. Выводы Рена совпадали с выводами Гюйгенса.
Мемуар Гюйгенса был представлен позже других (в первых числах января 1669 г.) и напечатан в Англии через несколько месяцев после мемуаров Валлиса и Рена. Не дождавшись его публикации в Англии, обиженный Гюйгенс опубликовал уже в марте во Франции{108}резюме своих выводов. Мы не будем вдаваться в рассмотрение возникших приоритетных споров и в разбор мемуара 1669 г., обратившись прямо к той более полной редакции, которая увидела свет лишь после смерти Гюйгенса (1695), — в издании его посмертных трудов (1703). Этот трактат — «О движении тел под влиянием удара» — один из шедевров механики XVII в.
Гюйгенс ограничился рассмотрением центрального удара упругих тел, состоящих из одного и того же вещества. Исходной точкой при рассмотрении соударения одинаковых масс является для него следующая аксиома (1-е правило Декарта): если два равных тела (шара) сталкиваются друг с другом с одинаковыми, но противоположно направленными скоростями, направление их движения меняется на противоположное без изменения скорости.
При неодинаковых скоростях (но при равных массах) Гюйгенс, основываясь на относительности движения, прибег к остроумному приему, позволившему свести все далее рассматриваемые случаи к первому аксиоматическому. Именно: он представил себе, что удар происходит в лодке, движущейся с постоянной скоростью вдоль ровного берега. Согласно классическому принципу относительности, в явлениях удара ничего не должно меняться. Величину скорости лодки в каждом новом случае выбирают такой, чтобы для наблюдателя, находящегося на берегу, явление сводилось к первому случаю, уже ранее разобранному.
Вскоре после конкурса, проведенного Лондонским королевским обществом, Мариотт напечатал свой «Трактат об ударе или соударении тел» (1678), выдержавший три издания (1679, 1684). Отправляясь от работ Гюйгенса, Валлиса и Рена, он дополнил их исследования новыми многочисленными экспериментами, производившимися им начиная с 1674 г.

ХРИСТИАН ГЮЙГЕНС (1629—1695)
Нидерландский механик, физик и математик. Создал волновую теорию света. В сочинении «Маятниковые часы» Гюйгенс ввел понятия центробежной и центростремительной силы и моментов инерции, исследовал движение математического и физического маятника
Для изучения явлений удара Мариотт придумал прибор, состоящий из двух шаров, подвешенных на двух нитях равной длины и находящихся в соприкосновении в состоянии равновесия. Он начал с изучения удара пластичных тел, беря шарики из глины. Скорости он измерял дугами, описываемыми шариками после столкновения.
В 80-х годах XVII в., упомянув о трудах Рена, Валлиса, Гюйгенса и Мариотта, Ньютон посвятил несколько страниц своих «Начал» произведенным им самим экспериментам. Однако главное, что внес Ньютон в изучение удара, это не столько новые эксперименты, сколько та связь, которую он установил между явлениями удара и формулированным им законом равенства действия и противодействия.
Связь законов удара с законом действия и противодействия Ньютон раскрывает в следующих словах: «Если какое-нибудь тело, ударившись в другое тело, изменяет своею силою его количество движения на сколько-нибудь, то оно претерпит от силы второго тела в своем собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих же тел друг на друга постоянно равны. От таких взаимодействий всегда происходят равные изменения не скоростей, а количества движения, предполагая, конечно, что тела никаким другим усилиям не подвергаются. Изменения скоростей, происходящие также в противоположные стороны, будут обратно пропорциональны массам тел, ибо количества движения получают равные изменения»{109}.
Что касается существа собственных опытов, Ньютон изложил их в следующих словах: «Производя испытания над маятниками длиною 10 футов и над массами, равными и неравными, и пуская тела так, чтобы они встречались, пройдя большие промежутки, например 8, 12, 16 футов, я получал с ошибкою, меньшею 3 дюймов, в измерениях, что при прямом ударе между телами изменения их количеств движения были равны и направлены в стороны противоположные, откуда следует, что действие и противодействие между собой равны… То же самое происходит и при движении тел в одну сторону… Подобное соотношение имеет место и в остальных случаях: полное количество движения, рассчитываемое, взяв сумму количеств движения, когда они направлены в одну сторону, и разность, когда они направлены в стороны противоположные, никогда не изменяется от удара при встрече тел»{110}.
Отсюда отчетливо выявляется неверность декартовской формулировки закона сохранения количества движения, не принимающей во внимание алгебраические знаки.
Ньютон отмечает, что описанные им опыты относятся к неупругим телам, — они «удаются как с телами мягкими, так и с жесткими, и совершенно не зависят от степени твердости их». В случае же тел упругих «необходимо лишь уменьшить скорость отражения сообразно степени упругости тел».
Итак, к 80-м годам уже было прекрасно осознано, что закон сохранения количества движения в том виде, как формулировал его Декарт, неправилен. Более того, если принять его в этом виде, с одинаковым успехом может быть доказано и бесконечное возрастание количества движения, т. е. «вечное движение», и, наоборот, убывание его.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Лекция 7. В поисках новых законов
Лекция 7. В поисках новых законов Строго говоря, то, о чем я собираюсь говорить в этой лекции, нельзя назвать характеристикой законов физики. Когда мы рассуждаем о характере физических законов, мы можем по крайней мере предполагать, что говорим о самой природе. Но теперь
Единство всех физических законов
Единство всех физических законов Решительное отступление от евклидовой геометрии произошло, когда Гаусс поручил студенту Риману подготовить доклад об «основах геометрии». Гаусс всерьез заинтересовался вопросом, сумеет ли его ученик разработать альтернативу
Открытия П. и М. Кюри
Открытия П. и М. Кюри Вернемся к радиоактивности. Беккерель продолжал исследование открытого им явления. Он считал его свойством урана, аналогичным фосфоресценции. Уран, по мнению Беккереля, «представляет первый пример металла, обнаруживающего свойство, подобное
История открытия нейтрона
История открытия нейтрона История открытия нейтрона начинается с безуспешных попыток Чедвика обнаружить нейтроны при электрических разрядах в водороде (на основе вышеупомянутой гипотезы Резерфор-да). Резерфорд, как мы знаем, осуществил первую искусственную ядерную
История открытия нейтрона
История открытия нейтрона История открытия нейтрона начинается с безуспешных попыток Чедвика обнаружить нейтроны при электрических разрядах в водороде (на основе вышеупомянутой гипотезы Резерфор-да). Резерфорд, как мы знаем, осуществил первую искусственную ядерную
ИСТОРИЯ ОТКРЫТИЯ ЗАКОНА ТЯГОТЕНИЯ
ИСТОРИЯ ОТКРЫТИЯ ЗАКОНА ТЯГОТЕНИЯ Декарт писал 12 сентября 1638 г. Мерсенну: «Невозможно сказать что-либо хорошее и прочное касательно скорости, не разъяснив на деле, что такое тяжесть и вместе с тем вся система мира»{111}. Это заявление диаметрально противоположно заявлению
1. История открытия явления катализа
1. История открытия явления катализа Катализ – изменение скорости химической реакции в присутствии катализаторов. Самые простые научные сведения о катализе были известны уже к началу XIX в. Знаменитый русский химик, академик К. С. Кирхгоф, открыл в 1811 г. каталитическое
2. На грани открытия
2. На грани открытия Итак, Луна интересует всех! Штурм ее начался в 1959 году, когда весь мир услышал сообщение ТАСС о том, что «2 января в СССР успешно запущена первая космическая ракета „Луна-1“ („Мечта“), направленная в сторону Луны и ставшая первой искусственной планетой
Открытия не умирают
Открытия не умирают Живя в век космоса и атома, естественно равняться на науку этого века. Но нельзя бросаться в крайность — пренебрежительно отвергать все то, что было найдено предшественниками.Да, «девяносто процентов всех ученых живы, работают рядом с нами». Но если бы
1. Люди и открытия
1. Люди и открытия Они стали говорить на разных языках. Они познали скорбь и полюбили скорбь Они жаждали мучения и говорили, что истина достигается лишь мучением. Тогда у них явилась наука. Ф. М. Достоевский. Сон смешного человека Об открытиях мы слышим и читаем почти
ПЕРВЫЕ ОТКРЫТИЯ
ПЕРВЫЕ ОТКРЫТИЯ Несмотря на то что Дэви принял Фарадея на работу, чтобы тот просто мыл пробирки и выполнял аналогичные задания, Майкл согласился на эти условия, пользуясь любой возможностью для того, чтобы приблизиться к настоящей науке.Некоторое время спустя, в октябре
Приоритет квантовых законов
Приоритет квантовых законов Наша Вселенная в основе своей квантовая. Под этим я имею в виду, что всё в ней флуктуирует, то есть случайным образом колеблется. Хотя бы чуть-чуть, но абсолютно всё!Когда мы используем высокоточные инструменты для изучения крохотных