ЗАДАЧА О ВРАЩЕНИИ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ

ЗАДАЧА О ВРАЩЕНИИ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ

Проблема вращения твердого тела — характерный пример тех механико-математических проблем, которые стояли в центре теоретической механики во второй половине XIX в. Начиная с С.В. Ковалевской (1850—1891), русские ученые вносят крупный вклад в решение этой проблемы. Факты богатой событиями биографии Ковалевской и оценку ее математических работ можно почерпнуть из весьма обширной литературы. Мы остановимся лишь на главных вехах ее жизни.

С 1868 г. С.В. Ковалевская, жившая до того в Москве, вступила в брак с В.О. Ковалевским (впоследствии знаменитым палеонтологом) и уехала с ним в Петербург, где обратилась к П.Л. Чебышеву с просьбой разрешить ей слушать его лекции в университете. Но в силу законов того времени она, будучи женщиной, не могла быть допущена на эти лекции. В 1869 г. Ковалевские уехали за границу. Здесь Ковалевская систематически изучала математику и физику, посещая в Гейдельбергском университете лекции крупнейших ученых того времени. Через два года она переехала в Берлин, где преподавал Карл Вейерштрасс (1815—1897).

СОФЬЯ ВАСИЛЬЕВНА КОВАЛЕВСКАЯ (1850-1891)

Русский математик и механик, первая в мире женщина-профессор, член-корреспондент Петербургской академии наук. Ей принадлежат фундаментальные работы по теории дифференциальных уравнений и по механике. С.В. Ковалевская внесла крупный вклад в решение задачи твердого тела 

В Берлинский университет женщин тогда тоже не допускали, и Вейерштрасс начал заниматься с Ковалевской частным образом.

Вейерштрасс был очень высокого мнения о математическом даровании своей ученицы. «Что же вообще касается уровня математического образования г-жи Ковалевской, — писал он геттингенскому математику Л. Фуксу в письме от 27 июня 1874 г., — то я могу с уверенностью сказать, что у меня было очень мало учеников, которые могли бы сравниться с ней в том, что касается ее способностей, суждений, прилежания и любви к науке»^{214}.

Ковалевская становится любимой ученицей Вейерштрасса. Он не только повторяет ей одной лекции, читаемые им в университете, но знакомит ее также со своими неопубликованными работами и обсуждает животрепещущие научные проблемы.

В 1874 г. Геттингенский университет заочно присуждает С.В. Ковалевской ученую степень доктора философии. В качестве докторской диссертации Ковалевская представила три работы, из которых особенно замечательна работа «К теории уравнений в частных производных». Здесь была доказана классическая теорема существования голоморфного решения системы дифференциальных уравнений в частных производных нормального вида. В современных курсах математического анализа эта теорема называется ее именем.

В 1874 г. С.В. Ковалевская возвратилась в Россию. Начался самый тяжелый период ее жизни. Ковалевская, уже признанный за границей математик, хотела приложить свои знания на родине, но в царской России женщина не могла получить кафедру в университете.

В конце 1879 г. П.Л. Чебышев предложил Ковалевской сделать сообщение о ее математических работах на VI съезде русских естествоиспытателей в Петербурге. В том же году Ковалевские переехали в Москву. Софья Васильевна решила сдать в Московском университете магистерские экзамены, но не была к ним допущена.

В 1881 г. Ковалевская снова у Вейерштрасса, полная творческого энтузиазма и страстного желания подготовить как можно больше математических работ. В течение двух лет она занимается проблемой света в кристаллах.

В августе 1883 г. Ковалевская делает доклад на VII съезде русских естествоиспытателей о преломлении света в кристаллах. На этом съезде она познакомилась с Н.Е. Жуковским.

В ноябре 1883 г. профессор Стокгольмского университета выдающийся математик Г. Миттаг-Леффлер (1846—1927) предложил Софье Васильевне место доцента. Она согласилась и переехала в Стокгольм. В 1884 г. Ковалевская стала профессором в том же университете. За восемь лет своей работы в Стокгольме Софья Васильевна прочитала двенадцать курсов по различным разделам математики и механики. В Швеции она пользовалась большой популярностью не только как выдающийся математик, но и как незаурядная писательница.

В 1888 г. С.В. Ковалевская написала свою знаменитую работу «Задача о вращении твердого тела около неподвижной точки». Выше уже говорилось об истории этой задачи. Еще в 1758 г. Эйлер рассмотрел случай движения твердого тела вокруг неподвижной точки (полюса), когда центр тяжести совпадает с полюсом, а все силы сводятся к равнодействующей, проходящей через эту неподвижную точку. Л. Пуансо (1777—1859) в 1834 г. дал геометрическую интерпретацию этого случая. В 1788 г. Лагранж (и независимо от него в 1815 г. Пуассон) рассмотрел случай, когда тело имеет ось симметрии, проходящую через неподвижную точку, и движется под действием только силы тяжести, точка приложения которой лежит на оси симметрии и не совпадает с полюсом. Обе задачи сводятся в общем случае к квадратурам, и решения выражаются через эллиптические функции. Все вычисления были выполнены до конца И.И. Сомовым в 1851 г.

После исследований Эйлера, Лагранжа и Пуассона проблема движения тела вокруг неподвижной точки длительное время не получала дальнейшего развития. Ввиду важности этой проблемы французская Академия наук назначила премии за какое-либо существенное продвижение в исследовании задачи. Два проведенных конкурса не дали результатов. В 1888 г. конкурс был объявлен в третий раз. Из пятнадцати представленных работ получила премию работа С.В. Ковалевской, имевшая девиз: «Говори, что знаешь; делай, что обязан; будь, чему быть». Конкурсная комиссия, в состав которой входили крупнейшие ученые, увеличила премию с 3000 до 5000 франков, так как, по заключению комиссии, работа Ковалевской является «замечательным трудом, который содержит открытие нового случая …автор не удовольствовался прибавлением результата к тем решениям, какие перешли к нам по этому предмету от Эйлера и Лагранжа, а сделал из своего открытия углубленное исследование с применением всех возможностей современной теории функций»^{215}.

В начале своей работы Ковалевская ставит вопрос: не существует ли кроме случаев, рассмотренных Эйлером и Лагранжем, еще других случаев движения твердого тела вокруг неподвижной оси, которые могли бы быть выражены при помощи каких-либо функций времени, аналогичных функциям, примененным для исследования первых двух задач? В результате своих изысканий она находит, что применение подобных функций позволит разрешить только один новый случай движения твердого тела. В этом случае центр тяжести тела лежит в плоскости экватора эллипсоида инерции, построенного для неподвижной точки.

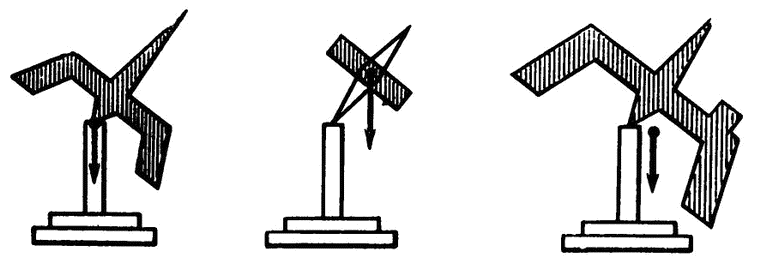
В работе Ковалевской о вращении тяжелого твердого тела вокруг неподвижной точки необходимо отметить следующие существенно новые для механики и математики особенности. Ею открыт новый случай вращения твердого тела вокруг неподвижной оси, для которого она нашла общий интеграл. Этот случай справедливо получил ее имя. В своем труде С.В. Ковалевская впервые привлекла к исследованию подобных задач прекрасно разработанный аппарат теории функций комплексного переменного. Наконец, ее работа поставила некоторые новые общие математические проблемы. Н.Е. Жуковский построил наглядные модели волчков для всех трех решенных в конечном виде случаев вращения твердого тела: первый из приведенных рисунков характеризует случай Эйлера — Пуансо, второй — случай Лагранжа — Пуассона, и третий — случай Ковалевской (см. рисунок).

Работы С.В. Ковалевской, посвященные движению твердого тела, стали исходным пунктом многочисленных исследований. Мы можем назвать русских ученых, так или иначе дополнивших анализ Ковалевской: московских профессоров Г.Г. Аппельрота (1866—1943), П.А. Некрасова, Б.К. Млодзеевского (1859—1923), Н.Е. Жуковского, а также А.М. Ляпунова и Н.Б. Делоне.