ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
За свою почти сорокалетнюю научную деятельность Михаил Васильевич Остроградский (1801 —1861) создал ряд ценных трудов по основным проблемам механики. Ему принадлежат первоклассные исследования по методам интегрирования уравнений аналитической механики и разработке обобщенных принципов статики и динамики.
Многочисленные исследования М.В. Остроградского по механике можно разбить, как это сделал Н.Е. Жуковский, на три группы: 1) работы по началу возможных перемещений, 2) работы по дифференциальным уравнениям механики и 3) работы по решению частных механических задач.
Наиболее выдающиеся исследования Остроградского относятся к обобщениям основных принципов и методов механики. Он внес существенный вклад в развитие вариационных принципов. Вариационные принципы механики входят в круг вопросов, интересовавших Остроградского в течение всей его жизни. Постоянное возвращение к вариационному исчислению и вариационным принципам механики роднит его с Лагранжем — одним из создателей вариационного исчисления и творцом аналитической механики. Ранее нами указывалось, что вариационными принципами механики занимались такие корифеи науки, как Ферма, Мопертюи, Эйлер, Лагранж, Гамильтон. Мы также отметили, что новый этап в разработке принципа наименьшего действия связан с именем Лагранжа, который поставил целью свести динамику к чистому анализу. В работах Лагранжа проблемы механики представляют собой лишь определенный класс задач вариационного исчисления.
Такой же подход к механике характерен и для Остроградского, который рассматривал ее проблемы, как правило, в самом общем виде. Общая постановка вопроса вела в свою очередь к изучению вариационного исчисления, в которое как частный случай входит динамика. Поэтому мемуар Остроградского «О дифференциальных уравнениях, относящихся к задаче изопериметров» (1850) принадлежит в равной мере как механике, так и вариационному исчислению. В силу такого сугубо математического подхода (как у Лагранжа) исследования Остроградского значительно обогатили, развили и углубили понимание вариационных принципов прежде всего с математической точки зрения.

МИХАИЛ ВАСИЛЬЕВИЧ ОСТРОГРАДСКИЙ (1801-1861)
Русский математик и механик, основатель аналитической механики в России. М.В. Остроградский разрешил ряд важных задач в области гидродинамики, гидростатики, теории упругости, теории теплоты, баллистики. Автор многочисленных трудов по математике и небесной механике
В названном мемуаре Остроградский рассматривает вариационную задачу, в которой подынтегральная функция зависит от произвольного числа неизвестных функций и их производных сколь угодно высокого порядка, и доказывает, что задача может быть сведена к интегрированию канонических уравнений Гамильтона, которые можно рассматривать как такую форму, в которую можно преобразовать любые уравнения, возникающие в вариационной задаче. Это преобразование не требует никаких операций, кроме дифференцирования и алгебраических действий. Заслуга такого обобщения задачи динамики принадлежит М.В. Остроградскому.
Кроме того, Остроградский ослабил ограничения на связи, всегда считавшиеся до него стационарными, и тем самым существенно обобщил проблему.
В 1850 г. Остроградский опубликовал еще один мемуар, содержащий важные результаты по математической теории уравнений движения, — «Об интегралах общих уравнений динамики» (представлен в 1848 г.). Он показал, что и в более общем случае, когда связи и силовая функция содержат время (этот случай был оставлен в стороне Гамильтоном и Якоби), уравнения движения также могут быть преобразованы в гамильтонову форму.
Одним из важных вопросов механики является задача интегрирования уравнений движения, которые составляют вариационный принцип. Разработка теории интегрирования канонических уравнений принадлежит Гамильтону, К. Якоби и Остроградскому.
Эта теория состоит из трех основных этапов. Прежде всего необходимо было найти наиболее простую возможную форму дифференциальных уравнений движения. Такой формой оказались канонические уравнения; они получили свое название благодаря замечательному свойству инвариантности относительно некоторых преобразований координат. Термины «канонические уравнения», «канонические преобразования» были введены Якоби.
Следующим этапом является установление общих законов подобных преобразований. Так была развита теория канонических преобразований и их инвариантов. Отсюда видно, что существует глубокая внутренняя связь между аналитической динамикой и общей теорией групп преобразований. Впоследствии эта связь была открыта норвежским математиком Софусом Ли (1842—1899), и вся теория приняла удивительно стройный и красивый вид: в механику вошли новые идеи, характерные для математики конца XIX в. Якоби показал, что существует такое каноническое преобразование, которое приводит исходные уравнения к новым, легко интегрируемым уравнениям. Таким образом, задача прямого интегрирования канонических уравнений заменяется другой математической задачей: найти вид соответствующего канонического преобразования. Наконец, остается задача интегрирования канонических уравнений. Оказалось, что интегрирование этих уравнений равносильно интегрированию уравнения в частных производных, так называемого уравнения Гамильтона — Якоби.
В разработку всей этой теории существенный вклад внес М.В. Остроградский. В исследованиях по уравнениям динамики он дал каноническую форму уравнений динамики и установил теоремы о характеристической функции, принимая связи системы зависящими от времени. В работах этого цикла независимо от Гамильтона и Якоби он развивает также и теорию того уравнения в частных производных, которое обычно называется уравнением Гамильтона — Якоби. Независимо от Гамильтона и Якоби Остроградский доказал, что задача определения интегралов канонических уравнений эквивалентна нахождению полного интеграла некоторого дифференциального уравнения в частных производных. Все искомые интегралы канонических уравнений можно найти дифференцированием полного интеграла уравнения в частных производных.
«По своей ясности, — писал Н.Е. Жуковский, — рассматриваемый мемуар Остроградского («Об интегралах общих уравнений динамики». — А. Г.) являлся по тогдашнему времени весьма ценным изложением теории интегрирования уравнений динамики и может с успехом служить для лекционных целей и в настоящее время»{179}.
Остроградский придавал большое значение изучению величин, инвариантных относительно преобразований координат. Он отмечает свойство инвариантности канонических уравнений и дает этому факту совершенно правильное объяснение: причина заключается в том, что само движение не зависит от выбора системы координат.
Работы Остроградского по динамике являются основополагающими. Их значение состоит еще в том, что они послужили источником для ряда дальнейших исследований по выяснению основ вариационных принципов механики.
Под влиянием работ Остроградского многие русские ученые внесли большой вклад в развитие вариационных принципов механики. В работах Н.Д. Брашмана, И.И. Сомова, М.И. Талызина, Ф.А. Слудского, Н.Е. Жуковского, Г.К. Суслова, Д.К. Бобылева и других ученых был решен комплекс вопросов о характере вариации в принципе наименьшего действия в форме Лагранжа и о методе вывода из него уравнений движения механики. Глубоко изучена была также строгая математическая форма самого принципа наименьшего действия и его связь с уравнениями движения. Выяснение этих вопросов было необходимо для того, чтобы принцип наименьшего действия стал не только безупречным основанием аналитической механики, но и мощным методом исследования в различных областях физики.
Действительно, роль принципа Гамильтона — Остроградского в дальнейшем развитии физико-математических наук оказалась весьма значительной. Теперь трудно указать такую область механики, физики, где мы не встретились бы в той или иной форме с применением принцип на Гамильтона — Остроградского.
Из других важных трудов Остроградского по механике следует отметить его исследование о принципе возможных перемещений «Общие соображения относительно моментов сил» (1834 г., опубликовано в 1838 г.). Эта работа значительно расширила область применения принципа возможных перемещений, распространила его на так называемые освобождающие (или неудерживающие) связи.
Исследования Остроградского по принципу возможных перемещений являются непосредственным продолжением работ Лагранжа и обобщением его идей. Так считал и сам Остроградский, писавший: «Лагранж не удовлетворился тем, что вывел следствия из принципа И. Бернулли, но расширил и обобщил самый принцип и приложил его к решению труднейших вопросов равновесия и движения систем. Затем вопрос сочли исчерпанным и полагали, что ничего нельзя уже прибавить к теориям, установленным Лагранжем. Однако принцип виртуальных скоростей еще шире, чем предполагал сам Лагранж, который, как и Бернулли, считал, что для равновесия системы необходимо, чтобы полный момент, т. е. сумма моментов всех сил, был равен нулю для всех перемещений, которым может быть подвержена система»{180}.
Под моментом сил Остроградский подразумевал работу сил. Итак, здесь ученый развивает мысль о распространении метода возможных перемещений на системы с освобождающими связями, поставив условием равновесия требование, чтобы полный момент сил был равен нулю или меньше нуля. Этот же метод был применен Остроградским для вывода дифференциальных уравнений движения, причем эти уравнения были выведены Остроградским и для случая голономных освобождающих связей, и для дифференциальных (неголономных) связей линейного вида.
В работах «О мгновенных перемещениях систем, подчиненных переменным условиям» (1838) и «О принципе виртуальных скоростей и о силе инерции» (1841 г., опубликована в 1842 г.) Остроградский дал строгое доказательство формулы, выражающей принцип возможных перемещений, для случая нестационарных связей. Во второй работе указаны некоторые неточности, допущенные Пуассоном в курсе механики.
Лагранж в «Аналитической механике» рассмотрел многие вопросы этой науки, но одна интересная задача теории удара была оставлена им в стороне; частный случай ее был изучен вскоре Л. Карно. В мемуаре «К общей теории удара» (1854 г., опубликован в 1857 г.) Остроградский исследовал удар систем в предположении, что возникающие в момент удара связи сохраняются и после него. Он распространил здесь принцип возможных перемещений на явление неупругого удара и получил основную формулу аналитической теории удара, из которой легко получается ряд теорем, решение упомянутой задачи, и в частности обобщение одной теоремы Карно. М.В. Остроградский читал лекции по аналитической механике. Курс, читанный им в Институте инженеров путей сообщения, был литографирован в 1834 г. По словам коллеги Остроградского, известного математика В.Я. Буняковского, выход этого сочинения ожидался с нетерпением. Позднее, в 1852 г., вышли в литографическом издании лекции по аналитической механике, читанные Остроградским в Главном педагогическом институте. Эти лекции Остроградского, составленные на основе классических работ Лагранжа, а также новейших работ Фурье (1768—1830), С. Пуассона (1781—1840), Гамильтона и самого лектора, имели большое значение для распространения физико-математических наук в России. Изложение Остроградского во многом оригинально. Он искал в механике наиболее простые и общие принципы, позволяющие доказывать ее теоремы изящно, кратко и просто.
Выдающийся советский ученый академик Алексей Николаевич Крылов в своем предисловии к новому изданию этих лекций говорил о богатстве их содержания и своеобразии изложения. В докладе Президиуму АН СССР Крылов писал: «Эта книга не только будет служить некоторым памятником знаменитому ученому, но принесет большую пользу как пособие для вузов и втузов».
Остроградскому принадлежат не только общие теоретические труды широкого охвата, но и работы, содержащие решения конкретных частных задач механики, возникших в технической практике того времени. Особого упоминания заслуживает серия его работ по баллистике, предпринятая по заданию русского артиллерийского ведомства. Плодом этих занятий явились следующие его мемуары в этой области: «Заметка о движении сферического снаряда в сопротивляющейся среде» и «Мемуар о движении сферического снаряда в воздухе» (1840 г., опубликован в 1841 г.), а также «Таблицы для облегчения вычисления траектории тела в сопротивляющейся среде» (1839 г., опубликовано в 1841 г.). В первых двух работах Остроградский исследовал актуальный для артиллерии того времени вопрос о движении центра тяжести, о вращении сферического снаряда, геометрический центр которого не совпадает с центром тяжести. Здесь был сделан существенный шаг вперед по сравнению с несколько более ранними исследованиями Пуассона, который изучил движение сферических снарядов в допущении, что эти два центра совпадают.
Третье упомянутое сочинение заключает в себе вычисленные Остроградским таблицы функции
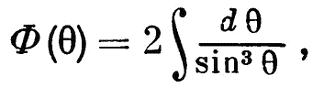
которая играет весьма важную роль в баллистике. Эти работы послужили одной из основ для создания во второй половине XIX в. русской школы баллистики, блестящими представителями которой впоследствии явились П.Л. Чебышев, Н.В. Маиевский, Н.А. Забудский и др.
Стоит отметить также, что в последние годы жизни М.В. Остроградский дважды прочитал курс баллистики в Артиллерийской академии. Подчеркнем также, что труды Остроградского по баллистике и по небесной механике привели его к открытию важных формул в области приближенных вычислений.
Подведем итог краткому разбору основных трудов Остроградского по механике выразительной характеристикой, принадлежащей Н.Е. Жуковскому: «Большая часть ученых работ М.В. Остроградского относится к его любимому предмету — аналитической механике. Он писал по разнообразным вопросам этого предмета: по теории притяжения, по колебанию упругого тела, по гидростатике и гидродинамике, по общей теории удара, по моменту сил при возможных перемещениях и т. д. Во всех его работах главное внимание сосредоточивалось не на решении частных задач, а на установлении общих теорий. Он с особенной любовью занимался расширением метода Лагранжа о возможных скоростях и установлением на самых общих началах теорем динамики. Его обширная работа «Об изопериметрах» заключает в себе как частные случаи различные предположения Лагранжа, Пуассона, Гамильтона и Якоби об интегрировании уравнений динамики. С именем М.В. Остроградского всегда будет связано распространение способа возможных перемещений на системы с освобождающими связями и изложение теорем динамики с помощью вариаций координат, происходящих от изменения произвольных постоянных»{181}.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
4. Принцип соответствия в новой механике
4. Принцип соответствия в новой механике Новая механика позволяет придать гораздо более точную форму принципу соответствия и частично устранить поводы для критики, которой он подвергался в рамках старой квантовой теории. Мы уже видели, как Бор пытался использовать
4. Индетерминизм в новой механике
4. Индетерминизм в новой механике Уравнения классической механики целиком и полностью определяют движение системы, если в начальный момент времени известны положения и состояния движения каждой из ее частей. Таким образом, можно полностью предсказать классическое
3. Труды деятелей физической науки
3. Труды деятелей физической науки Ампер. Электродинамика. Серия «Классики науки».— М.: Изд-во АН СССР, 1954.Аристотель. Аналитики первая и вторая.—Я: Госполитиздат, 1952Аркадьев В. К. Избранные труды. — М.: Изд-во АН СССР, 1961.Архимед. Сочинения.—М: физматгиз, 1962.Бернулли Д
РАБОТЫ БЕРНУЛЛИ И ЭЙЛЕРА ПО МЕХАНИКЕ ЖИДКОСТЕЙ И ГАЗОВ
РАБОТЫ БЕРНУЛЛИ И ЭЙЛЕРА ПО МЕХАНИКЕ ЖИДКОСТЕЙ И ГАЗОВ Проблема взаимодействия между жидкостью и частично или полностью погруженным в нее телом возникла из нужд практики в древности. Еще Архимед открыл закон, выражающий подъемную силу, которая поддерживает плавающее
ИССЛЕДОВАНИЯ ПУАССОНА ПО МЕХАНИКЕ
ИССЛЕДОВАНИЯ ПУАССОНА ПО МЕХАНИКЕ Симеон Дени Пуассон (1781 —1840) — выдающийся французский механик, математик и физик, научная деятельность которого тесно связана с традициями Политехнической школы. Эта школа была ведущим высшим учебным заведением Франции, поступающие в
Глава первая Опыты по механике
Глава первая Опыты по механике Рубль на листке бумаги. Положите на край стола открытку так, чтобы две трети ее выступали, а на открытку у самого края поставьте на ребро серебряный рубль или пятак (рис. 1). Конечно, это место стола не должно быть покрыто скатертью, и стол