ОБЪЕДИНЯЮЩИЙ ПРИНЦИП
Теория ван дер Ваальса значительно расширила круг интересов статистической механики, включив в него рассмотрение жидкого состояния вещества, а ее автор заслуженно удостоился мировой славы. Максвелл писал, что «ван дер Ваальс, несомненно, станет одним из самых авторитетных ученых в молекулярной физике»7. В 1910 году ван дер Ваальсу была присуждена Нобелевская премия. В то же время его теория не внесла окончательной ясности в проблему, так как она объясняла лишь некоторые фазовые переходы и не позволяла, например, описать замерзание и плавление, относящиеся к превращениям жидкости в твердое тело, и наоборот. Однако в дальнейшем эта теория нашла широкое применение в других разделах физики.
Дело в том, что проблема фазовых переходов неожиданно оказалась связанной с множеством других процессов. Например, еще с древности былс известно, что магниты теряют намагниченность при нагревании и восстанавливают ее при охлаждении. Для магнитного железа такое превращение происходит при нагреве до 770 °С, что умели делать даже средневековые кузнецы В том же самом 1873 году, когда ван дер Ваальс защитил свою диссертацию английский физик Уильям Баррет предположил, что размагничивание пр? нагреве происходит не постепенно, а сразу и при определенной температуре что, естественно, напоминало фазовые переходы.
В 1889 году Джон Хопкинсон из лондонского Кингз-колледжа, оцениі количественно потерю магнитных свойств при нагреве, получил чрезвычайно интересный результат: математическое описание этого процесса соответствовало взаимопревращению жидкость—газ вблизи критической точки. Очені часто это открытие приписывают знаменитому французскому физику Пьер} Кюри (мужу Марии Кюри), который действительно получил такой же результат в 1895 году, и поэтому француз Пьер Вейс, создавший в 1907 году теорик магнитных переходов, даже назвал температуру магнитного фазового переходе точкой Кюри, в память своего друга, погибшего в дорожной аварии[34].
Атомы в твердом теле, например в куске железа, располагаются вовсе не хаотически, как в жидкостях и газах, а вполне упорядоченно и почти неподвижно (подобно яйцам в специальной упаковке, продаваемой в любом магазине). Тем не менее Вейсу удалось применить для таких упорядоченных систем подход ван дер Ваальса, разработанный для флюидов вблизи критической точки. Как же так?!
Чтобы понять это, нам необходимо рассмотреть модель магнетизма, предложенную в 1920-х годах, уже после работ Вейса, немецким физиком Вильгельмоі? Ленцем. Кусок железа проявляет магнитные свойства потому, что каждый и: составляющих его атомов железа ведет себя подобно крошечному магниту. Читатель может представить себе атомы в виде маленьких намагниченных иголок которые обладают свойством выстраиваться в линию друг за другом. Физике называют такую «атомную иголку» спином, хотя ни о каком реальном вращение «иголки» речи при этом не идет (английское spin означает вращение). В куске железа направление каждого такого спина определяется совместным магнитньп? полем, создаваемым окружающими его спинами или атомами. При этом, однако каждый из спинов и сам воздействует на ближайшее окружение, т.е. на атомы і ближайших узлах кристаллической решетки. Обычно магнитное взаимодействие заставляет «иголки» выстраиваться в соответствии с окружением. Наиболее стабильным состоянием атомной решетки при этом является ситуация, когд< все «иголки» направлены в одну сторону. В этой конфигурации очень малые магнитные поля отдельных атомов складываются и создают совместное, довольно мощное магнитное поле, проявления которого мы и замечаем.
Но любой нагрев такого образца нарушает упорядоченность атомов в полной аналогии с нарушением равновесия сил притяжения в жидкости. Тепловое воздействие как бы встряхивает решетку магнитных иголок, нарушая согласованность их взаимной направленности. При этом сами атомы еще сохраняют порядок в решетке, но направления их спинов разупорядочива- ются, в результате намагниченность образца в целом резко уменьшается.
Является ли предлагаемая модель размагничивания аналогом испарения жидкости? Не очевидно. С одной стороны, описываемый магнитный переход тоже происходит при строго определенной температуре (точке Кюри), однако с другой — он не является столь резким, т. е. уменьшение намагниченности в окрестности этой точке происходит постепенно. Поэтому представляется более правдоподобным, что точка Кюри скорее соответствует критической точке в системе «жидкость—газ», где различия между этими состояниями вещества становятся незаметными.
Это превращение и есть настоящий фазовый переход, так как свойства вещества четко изменяются: ниже точки Кюри — магнит, выше — не магнит. Но это другой тип фазовых переходов, отличный от испарения, конденсации, плавления и замерзания вещества, поскольку при нем не происходит скачкообразного изменения наблюдаемых характеристик объекта. Поэтому фазовые переходы, происходящие в критических точках, физики, вполне естественно, называют критическими фазовыми переходами, а иногда, по их физическим резонам, фазовыми переходами второго рода. Те же фазовые переходы, в которых макроскопические характеристики образца, например, плотность, изменяются скачком, называются фазовыми переходами первого рода (рис.4.1).
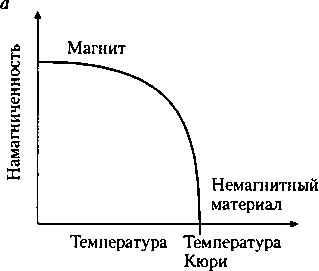
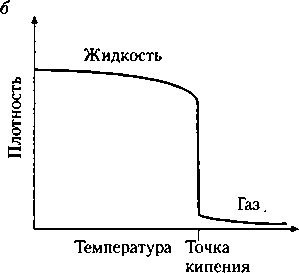
Рис. 4.1. Два разных типа фазовых переходов: а) при критических фазовых переходах (переходах второго рода) некоторые характеристики системы, например, намагниченность, постепенно уменьшаются до нуля при изменении некоторого «контрольного параметра», например, температуры; б) при фазовых переходах первого рода (типа замерзания или кипения жидкости) в точке перехода скачком изменяются некоторые характеристики вещества, например, плотность. Оба типа фазовых переходов нашли отражение в социальной физике.
Ленц придумал для описания магнитных фазовых переходов очень простую обобщающую модель, в рамках которой ориентация атомных магнитов менялась не непрерывно, а скачком, так что они могли принимать лишь два противоположных положения (условно: вверх или вниз). Таким образом, два соседних спина моіуг быть направлены только одинаково или противоположно, без всяких промежуточных состояний. Некоторые магнитные материалы действительно ведут себя в соответствии с предложенной моделью, забавно, но к этим материалам не относится железо, на основе изучения которого и возникла модель. Кроме этого, Ленц предположил, что любой атом в регулярной решетке способен воздействовать своим магнитным полем только на ближайших соседей.
В 1925 году студент Ленца Эрнст Изинг сумел описать поведение такой модельной системы атомов в простейшем случае. Понятно, что кристаллическая решетка реального магнита представляет собой упорядоченную трехмерную структуру, в которой у каждого имеется достаточно много «соседей». Существенно проще выглядит двумерный магнит, в котором атомы располагаются в перекрестьях плоской решетки, и каждый атом имеет всего несколько «соседей». Изинг упростил модель расположения атомов до формально простейшего случая одномерного магнита, когда атомы располагаются вдоль прямой линии, и каждый из них может взаимодействовать лишь с двумя непосредственными «соседями». Разумеется, такой подход является крайним упрощением для описания реальных, обладающих объемом кусочков железа, поэтому полученные Изингом на основе расчета такой системы результаты сперва показались разочаровывающими, так как получалось, что фазовый переход в таких одномерных магнитах может происходить лишь при абсолютном нуле (-273 °С). Только в этом случае направления всех спинов совпадали, но при малейшем нагреве порядок нарушался, и одномерная цепочка теряла свою намагниченность.
Сам Изинг никогда и не пытался добиться в физике чего-то большего. Окончив университет, он стал школьным преподавателем физики в Германии, а затем (после принятия антисемитских законов Гитлера в 1938 году) эмигрировал в США, где продолжал преподавать физику и умер глубоким старцем в возрасте 98 лет. Но на его долю выпало поразительное научное бессмертие, так как позднее модели, основанные на представлениях о «решетке» атомных магнитов, не только получили широчайшее распространение в разных разделах статистической физики, но и получили название моделей Изинга, хотя саму модель предложил Ленц.
Огромное значение модели Изинга состоит в том, что она позволяет описать разрушение системы частиц, связанных короткодействующими силами или взаимодействиями между отдельными частицами при тепловом воздействии. Для создания более реалистических описаний явлений окружающего мира эту модель, естественно, следовало распространить хотя бы на двумерные системы. Эта задача оказалась настолько трудной, что над ней ученые трудились более двадцати лет.
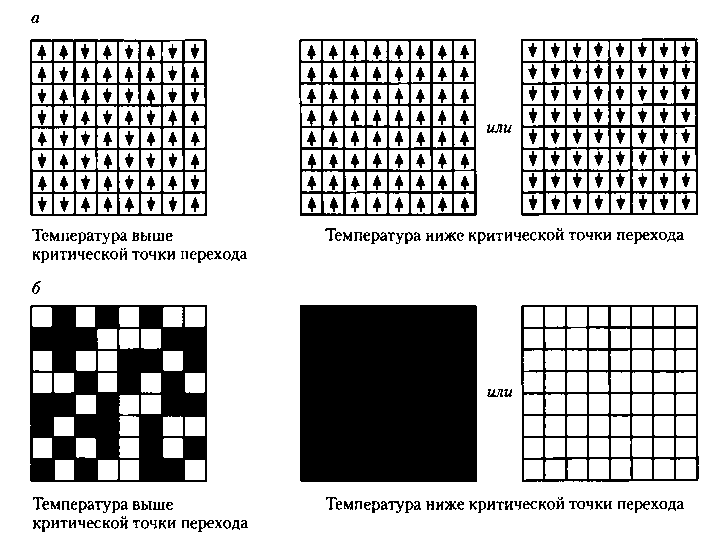
Рис. 4.2. Модель Изинга, предложенная для описания магнитных материалов:
а) «магнитные стрелки», или спины атомов, могут иметь лишь два противоположных направления. Атомная решетка может быть одномерной, двумерной (как показано на рисунке) или трехмерной. В намагниченном состоянии направления всех спинов совпадают, а выше критической температуры (под воздействием нагрева) становятся случайными, в результате чего материал теряет намагниченность. Аналогичная модель может быть использована для описания фазовых переходов между жидкостью и газом, когда они в критической точке образуют единое состояние флюида;
б) модель с двумя видами узлов решетки: занятыми (что соответствует конденсированному, жидкому состоянию вещества) и незанятыми (газообразное состояние). Выше критической точки такое вещество существует во флюидном состоянии с промежуточной плотностью.
Для объяснения поведения двухмерной (2-D) решетки Изинга норвежскому физику JIapcy Онсагеру (1903-1976) пришлось придумать чуть ли не новый раздел математики, что удалось сделать только к 1942 году[35]. Новая, двумерная модель магнита, напоминающая шахматную доску (рис. 4.2 а), в отличие от одномерной (1-D) не только позволяла получить фазовый переход от магнитного к немагнитному состоянию вещества при температурах выше абсолютного нуля, но и предсказывала критическую температуру перехода, значение которой было близко к точке Кюри для реальных магнитных материалов. Решения возникающих при этом задач оказались очень сложными, а разработка трехмерной модели, наиболее соответствующей физическим объектам, пока остается несбыточной мечтой теоретиков.
В наши дни ученые, сталкиваясь с неодолимыми задачами, не вздымают руки вверх, а опускают их на клавиатуру компьютера. Пусть алгебраические уравнения, описывающие трехмерную модель Изинга, пока не поддаются аналитическому решению, поведение 3-D систем можно моделировать на ЭВМ. В каком-то смысле это напоминает предсказания метеорологов, которые не могут точно решать сверхсложные уравнения, описывающие поведение атмосферных потоков, но могут приближенно рассчитать на компьютерах наиболее вероятные события. Поэтому неудивительно, что расчеты 3-D моделей Изинга чрезвычайно популярны в исследованиях фазовых переходов второго рода.
Однако необходимо еще раз обратиться к довольно сложному вопросу, почему ученые придавали столь большое значение аналогии между фазовыми переходами второго рода в жидкостях и магнитных материалах (физики называют их магнетиками). Конечно, в строении этих систем наблюдается некоторое общее сходство на атомарном уровне, однако нельзя не отметить и весьма существенные различия. Предположение, что эта аналогия означает нечто большее и решетка Изинга может использоваться в качестве грубой модели флюидов, высказал японский физик С. Оно в 1947 году, основываясь на присущей этим объектам «бинарности». Кстати, в двумерной модели читатель может представить себе вместо регулярной решетки атомов с противоположно направленными спинами (только вверх или вниз) эквивалентную, но гораздо более наглядную картину типа шахматной доски (рис. 4.2 б), в которой направления атомных спинов заменены цветом клеток или где темная клетка, например, соответствует занятому состоянию (или более плотному, жидкости), а светлая — незанятому (газообразному). Но задача заключается не только в выборе наглядных описаний, а содержит и более серьезные проблемы.
Дело в том, что между фазовыми переходами в этих двух разных системах обнаруживается довольное неожиданное и более глубокое сходство, о котором я упомяну здесь лишь в общих чертах (более подробно эти вопросы рассматриваются в гл. 10). Уже упоминалось, что при приближении к критической точке разница в плотностях жидкости и газа стремится к нулю. Более того, эту тенденцию можно описать количественно, т.е. точно вычислить, что если, например, при температуре, соответствующей 99% критической, отношение плотностей равно 2 (это означает, что плотность жидкости вдвое выше плотности газа), то при температуре 99,5% критической это отношение уменьшится до 1,5, и т.д. Для каждого флюида можно определить характеристическую скорость приближения к критической точке.
Сюрпризом для ученых оказалось, что почти так же ведут себя и магнитные материалы при приближении к точке Кюри (естественно, в них к нулю стремится не разность плотности, а общая намагниченность образца). Еще более неожиданным стало то, что скорости приближения к нулю этих разных характеристических параметров почти точно совпадают. Компьютерные расчеты для 3-D решеток Изинга показали, что и для них наблюдается аналогичная скорость «критического поведения», хотя решетка Изинга представляется всего лишь грубой моделью поведения флюидов и магнетиков. Эти три случая сильно различаются и по сути, и в деталях, но тем не менее демонстрируют совершенно одинаковые траектории «критического поведения».
Физики называют подобное сходство универсальностью, желая подчеркнуть, что в окружающем нас мире существуют процессы, протекающие одинаково и малочувствительные к конкретным деталям. Странно уже то, например, что кривые, соответствующие совершенно разным флюидам, таким как двуокись углерода и метан, с разными критическими температурами, ведут себя вблизи температуры фазового перехода одинаково. Тем более странно, что такие же кривые можно получить, изучая фазовый переход в некоторых классах магнитных материалов.
Это заставляет нас предположить, что фазовые переходы — общие явления: они протекают аналогично для совершенно разных систем. Поэтому физики могут часами обсуждать на своих семинарах проблемы фазовых переходов первого рода, и никто из них даже не спрашивает, о чем конкретно идет речь (о замораживании, испарении и т.д.), так как специалистам ясно, что доводы и выводы относятся к целому классу явлений. Специалисты по городскому движению тоже обсуждают проблемы автомобильных пробок, не конкретизируя названия улиц и перекрестков, как не имеющих особого значения при рассмотрении общих задач.
Сказанное может показаться очень широким обобщением наблюдаемого сходства переходов во флюидах и магнитах, однако проблема фазовых переходов содержит в себе еще много других неожиданностей.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК