ВСЕГДА ЛИ БОГАТЫЕ ПРОДОЛЖАЮТ БОГАТЕТЬ?

Сталкиваясь с одинаковым поведением разных систем, внешне не имеющих между собой ничего общего, ученые, естественно, начинают искать общий принцип, определяющий это поведение и позволяющий найти теоретическое объяснение, не связанное с конкретными особенностями изучаемых процессов. Например, мы уже не раз обсуждали проблему резких фазовых переходов в многочастичных системах, которые всегда оказывались связаны с конкуренцией сил, стремящихся упорядочить систему или перевести ее в состояние хаоса. Поэтому мы должны задуматься о существовании общего принципа, на основе которого в столь разных социальных системах мы сталкиваемся с возникновением безмасштабных сетей. Как может быть сформулирован этот принцип?

Мы начинали рассмотрение со случайных графов, изученных Эрдешем и Реньи, и малых миров, возникающих при переключении связей в круговом графе по методу Строгаца и Ваттса. Вспомним, что эти системы основаны и возникают по принципу чистой случайности. Анализируя социальные сети, Барабаши и Альберт заметили, что их рост носит не совсем случайный характер, например, при переключении связей некоторым предпочтением обладают узлы с большей связностью. Это хорошо иллюстрирует сеть связей киноактеров, поскольку новые актеры, естественно, стремятся сниматься с уже известными звездами, а не с подобными себе новичками. Чем выше известность и слава члена (узла) социальной сети, тем более привлекательным становится соседство с ним. С математической точки зрения это означает повышение вероятности создания новых связей в сети.

Легко заметить, что такой же «магнетизм славы» действует и в Паутине, и в сети, образуемой научными ссылками (кстати, это еще один пример безмасштабной системы). Понятно, что веб-страницы, уже содержащие большое количество входящих гиперссылок, становятся хорошо известными и привлекают еще больше ссылок. Люди чаще читают статьи, на которые чаще ссылаются коллеги, и в свою очередь ссылаются на прочитанные статьи и т.д. Другими словами, слава порождает новую славу.

Кто-то может заключить, что в основе этого лежит некий меритократи- ческий принцип, т. е. большее количество цитирования, большее число посещений сайта или более частое появление актера на экране свидетельствуют лишь о том, что именно эта научная статья, сайт или актер действительно являются хорошими. Но это далеко не всегда так. Слава притягивает, но сама слава бывает хорошей или дурной, обе в равной степени привлекательны. Думаю, читатели не затруднятся поиском собственных примеров этого.

Возвращаясь к научной стороне вопроса, отметим, что если бы каждый растущий граф имел тенденцию только к увеличению числа связей на уже самых связных вершинах, то рост должен был бы закончиться вовсе не безмасштабной сетью, а централизацией всех связей на одной-единственной вершине. Однако это практически никогда не происходит в растущих без плана сетях, что и наводит на мысль о еще каком-то механизме регулирования. Например, можно сразу отметить, что в очень больших, разросшихся графах ситуация изменяется, поскольку новой вершине очень трудно «найти» наиболее связную вершину, вследствие чего повышается вероятность связи с одной из менее загруженных вершин. Это обстоятельство прекрасно иллюстрируется ситуацией в мире кино: самые известные звезды не в состоянии сниматься подряд во всех новых фильмах. Таким образом, стремление к созданию связей с наиболее связной вершиной сети выступает не правилом, а лишь тенденцией, вероятностным смещением развития в определенную сторону.

Барабаши и Альберт смогли показать, что эта тенденция — лишь одна из особенностей роста безмасштабных сетей. Они предложили рассмотреть граф, растущий за счет добавления новых вершин, каждая из которых связывается с уже имеющимися вершинами случайным образом, но с некоторым предпочтением, которое отдается при этом более связным вершинам. Как оказалось, при этом образуется безмасштабная сеть. Рост многих финансовых и общественных организаций происходит по принципу «богатые всегда становятся еще богаче». Например, более крупные фирмы с большей вероятностью (хотя и не всегда) привлекут новых клиентов, что, кстати, частично объясняется и тем, что они могут обеспечить себе лучшую рекламу, т.е. создать больше «славы».

Аналогия станет яснее, если учесть, что в некоторых случаях число связей вершины может быть непосредственно связано с «богатством», например, если рассматривать связность вершины в качестве показателя числа связанных с фирмой клиентов. Если в обществе существует свобода выбора, а возможности фирмы привлечь новых клиентов зависят от числа уже имеющихся клиентов, то степенное распределение неравенства станет весьма вероятным исходом. Конечно, на любом свободном рынке имеются различия, например, в доступности ресурсов для разных торговцев, но процесс безмасштабного роста будет быстрее усиливать неравенство участников по сравнению со случайным распределением богатства. Результатом такого развития может стать заметное число «особых случаев» — очень богатых индивидов или чудовищных по размеру компаний. Социолог Джордж Кингсли Ципф еще в 1930-х годах указывал, что почти всегда в общественных явлениях мы наблюдаем действие степенного закона распределения по размеру компаний (гл. 11), городов и доходов (гл. 10).

Из этого не следует, что степенной закон неравенства неизбежен при свободном рынке. Но если мы сочтем такое неравенство нежелательным, нам скорее всего придется несколько ограничить те самые свободы, на которых построена деятельность рынка.

Следует, однако, отметить, что подобный рост сетей далеко не всегда приводит к такому большому неравенству. Джен Стэнли из университета Бостона, изучив роль и возможности безмасштабных сетей, описанных Бара- баши и Альберт, обнаружил ограниченность их применимости. Возьмем для примера уже привычную сеть киноактеров. Степенной закон распределения предсказывает наличие нескольких знаменитостей с огромным количеством связей, однако это не так, количество связей даже наиболее востребованных актеров заметно ниже предсказанного теорией (рис. 16.7)[143].

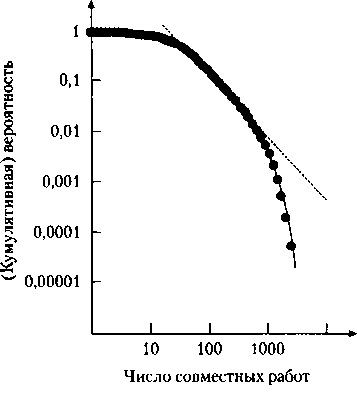
Рис. 16.7. Киноактеры с наибольшим количеством связей не вписываются в степенную зависимость, характеризующую всех прочих актеров, — те из них, кто имеет более трехсот совместных работ, обладают существенно меньшим количеством связей, чем предсказывает степенной закон. Другими словами, существует верхний предел совместных работ, в которых может принимать участие актер.

Что ограничивает применимость степенного распределения вероятностей? Стэнли и его сотрудники уверены, что ограничения связаны с реальными жизненными обстоятельствами, лимитирующими предельные проявления такого распределения. Даже самый талантливый и трудолюбивый актер за короткий срок человеческой жизни не может сняться, например, в тысяче фильмов. Аналогично старые научные статьи, даже самые значимые, рано или поздно перестают упоминаться, это вовсе не означает истинного забвения, просто современные ученые не читают старые работы, а ссылаются на последние обзоры или учебники. Ограничена пропускная способность аэропортов, а цены и локальная демография кладут предел росту самих аэропортов. Если вершины имеют некоторый предел насыщения по связям или их способность образовывать новые связи уменьшается со временем (аналог возраста), то безмасштабность структуры перестает действовать для наиболее связных вершин.

При некоторых других ограничениях степенное распределение вообще отходит на второй план, так как определенные социальные обстоятельства делают ничтожной вероятность возникновения суперсвязных центров. В качестве примера можно привести энергосеть южной Калифорнии или мировую сеть аэропортов, связанных маршрутами авиационных перелетов. Более того, Стэнли и его коллеги показали, что аналогичная ситуация обнаруживается и при анализе некоторых реальных социальных сетей типа группы из 43 близких друзей, принадлежащих к секте мормонов в штате Юта (где такие связи имеют прочную и давнюю традицию), или нескольких сотен студентов университета Мэдисон в штате Висконсин. Все такие социальные сети описываются гауссовским распределением, т. е. обладают некоторым «усредненным» значением связности. Но одновременно они являются и сетями малых миров, так как им присущ свойственный таким сетям медленный рост характеристической длины пути при увеличении числа узлов.

Обобщая сказанное, можно констатировать, что мы имеем дело с несколькими типами объектов, объединенных общим названием малых миров. С самого начала придуманные Строгацем и Ваттсом малые миры обладали только «одним масштабом», связанным с предпочтительным значением средней связности узлов и резким падением числа узлов с высокой связностью. В качестве противоположного варианта образования таких систем появились предложенные группой Барабаши безмасштабные сети, в которых «жадные» или «неразборчивые в связях» узлы не имеют пределов роста, и могут образовываться узлы с очень большой связностью. Как говорил сам Барабаши, между этими двумя крайностями возник и развился «целый зоопарк различных типов социальных сетей»¹². Независимо от точной топологии, сети малых миров почти никогда не формируются по плану или программе, а возникают сами собой в результате задаваемых законов соединения возникающих узлов с уже существующими.

Интересный взгляд на проблему предложили Ниш Матиас и Венкатеш Гопал из университета в Бангалоре (Индия), которые считают, что любая сеть такого типа представляет особый интерес с инженерной точки зрения, поскольку она всегда является некоторым идеальным компромиссом между двумя противоположными требованиями: максимизации количества связей между вершинами и минимизации общей длины этих связей. В общем случае соединение двух вершин в сети имеет вполне конкретное стоимостное выражение, понятно, что стоимость соединительного кабеля, трубопровода и т. п. растет пропорционально длине. Также очевидно, что наиболее эффективная связь в сети реализуется в том случае, если все вершины напрямую связаны друг с другом, но такое соединение оказывается чрезвычайно сложным и дорогим. Поэтому создатели сетей всегда предпочитают создавать систему с меньшим числом соединений, имеющих кратчайшую длину, в то время как пользователи систем всегда предпочитают иметь дело с большим числом соединений, имеющих большую длину (обеспечивающих, кстати, «короткие» пути). Матиас и Гопал показали, что первый набор требований лучше всего удовлетворяется в структурах, напоминающих регулярные решетки, а второй — в случайных сетях. Сети малых миров позволяют нам заменить очень дороіую и громоздкую регулярную решетку на более дешевую систему, обеспечивающую надежную связь на больших расстояниях.

Несмотря на то что физика сетей — совсем молодая наука, она уже позволила выявить ряд ценных закономерностей функционирования социальных структур. В настоящее время ученые только приступают к исследованию топологических особенностей сетей, которые соответствуют, например, распространению эпидемических заболеваний, культурных норм и т. д. В экономике становится все более очевидным, что именно анализ торговых сетей должен стать ключом к пониманию сложной динамики рыночных отношений. В заявлении организаторов семинара по эконофизике (институт Сан- та-Фе, 1996) отмечалось, что «функционирование рынков осуществляется сетями торговцев, поэтому события на рынке могут отражать структуру этих сетей, которая, в свою очередь, зависит от того, как эти сети возникли»¹³.

Появление теории сетей можно рассматривать в качестве естественного этапа в развитии статистической физики. С теоретической точки зрения новая теория представляет собой лишь вариант описания классической многочастичной системы, в которой сталкивающиеся частицы не разлетаются подобно бильярдным шарам, а образуют некие постоянные, упругие связи. Тем самым в структуре сети, в частности Интернета, отражается история ее создания. В сетях предыстория имеет значение, прошлое, образно говоря, «вморожено» в существующие формы и влияет на настоящее. Такие сети могут служить образом самой человеческой жизни, которая сплетается из огромного количества почти непонятных для нас самих нитей причин и следствий.