АВАРИЙНЫЙ ВЫХОД

В ночь на 23 ноября 1942 года жизнь в бостонском ночном клубе «Кокосовая роща» буквально била ключом. Многие отправляющиеся за океан военнослужащие прощались с друзьями, пиво лилось рекой, и громко играл блестящий джазовый оркестр. А потом вспыхнул страшный пожар. В клубе оказался всего один аварийный выход, куда и устремилась вся масса посетителей. Дверь отрывалась внутрь, но к тому моменту, когда первые беглецы смогли это выяснить, набежавшая толпа буквально впечатала их в дверь, так что открыть ее никак не удавалось. В заполненном дымом помещении никто не мог объяснить людям, что им для спасения необходимо хоть немного отодвинуться назад и дать возможность открыть проход. Толпа продолжала напирать, и в пламени погибли 492 человека.

15 апреля 1989 года толпа футбольных болельщиков в английском Шеффилде заполнила все улицы вокруг стадиона «Хиллсборо», отчаявшись попасть на полуфинальную встречу Кубка Англии между командами «Ливерпуль» и «Ноттинген Форест». Футбольные фанаты были столь настойчивы, что за десять минут до начала матча полиция решила пропустить их и открыла запасной проход на стадион, после чего ворвавшаяся толпа наткнулась на ограждение. Девяносто шесть человек были затоптаны насмерть[61].

На первый взгляд кажется, что предсказать поведение обезумевшей от паники толпы вообще невозможно. Любые планируемые меры предосторожности, рассчитанные на разумное поведение, теряют смысл, когда толпа превращается в орду обезумевших от страха людей. Что можно предложить для управления толпой в особых условиях? Прежде всего можно вспомнить, что иррациональное не означает непредсказуемого. Как ни странно это звучит, поведение паникующей толпы может быть предсказано довольно легко, так как фактором, управляющим людьми в таких ситуациях, выступа одно-единственное желание — убежать отсюда как можно быстрее! Кст ти, паническое бегство и бессмысленное поведение вызываются не толь страхом. Например, в 1979 году одиннадцать человек погибли в страшн< давке на концерте группы «The Two» в американском городе Цинциннат

В 1999 году Хелбинг перебрался в Будапешт для продолжения совмес ных работ с Тамашем Вицеком. Они собирались расширить предложенн) модель пешеходного движения на стадное поведение животных, одна: Вицек посчитал, что разработанные методы больше подходят для иссл дования человеческой толпы. Моделирование показало, что неустойчив состояние толпы (т.е. повышенный уровень «шума» в системе) мож приводить к усилению давки в дверях. Этот вывод, кстати, представл ется неожиданным с точки зрения физики, так как хаотичность в сре пиплоидов ассоциируется с температурой, повышение которой в груп частиц должно делать движения гораздо более энергичными[62]. Оказалос однако, что толпа в такой ситуации «замерзает», т.е. среда из отдельні элементов-людей может замерзнуть при нагреве индивидуальных элемент в отличие от нормальных физических сред, замерзающих при снижении температуры.

Хелбинг вместе с Илешем Фаркашем, коллегой Вицека по Будапеште* му университету, применили разработанную модель пешеходного движен для изучения неконтролируемого поведения толпы. В качестве основно критерия отличия панического поведения от нормы была принята гипоте о том, что при панике люди забывают о некоторых запретах и ограничен ях, т. е. начинают контактировать физически друг с другом, причем в так< степени, что нарастающее физическое давление может становиться да: опасным для их жизни (известно, что напор паникующей толпы способ сносить стальные преграды и сокрушать прочные кирпичные стены, что і говорить о ребрах!).

Сказанное вовсе не означает, что при панике у людей в толпе пропада естественное физическое отвращение к прямому контакту между собс просто этот фактор временно перестает быть доминирующим в их пове; нии. Результатом тесного сближения, естественно, становится значите.? ное ограничение подвижности, что каждый человек когда-либо испьп лично — вспомните, как трудно в давке не только повернуться, но и сделг нужное движение. Физическим аналогом этого выступает трение меж частицами, затрудняющее движение.

Теоретически введение таких ограничений и сил в модель Хелбиі можно осуществить очень просто, придав частицам-пиплоидам некотор коэффициент трения и превратив их, образно говоря, в бильярдные шары, покрытые наждачной бумагой. Для большей достоверности модели в нее дополнительно был введен также жестокий фактор, учитывающий возможность ранения пиплоида в давке, вследствие чего тот перестает двигаться. Кстати, это обстоятельство создает дополнительные препятствия массовому движению, увеличивая давление, которое, в свою очередь, способствует росту травматизма. Моделируя эти зависимости, исследователи старались понять закономерности поведения толпы при нарастании плотности потоков.

Разумеется, все эксперименты такого рода, особенно имитация пожаров и других несчастных случаев, осуществлялись лишь в виде компьютерных моделей, хотя стоит отметить и особые случаи[63]. В виртуальных экспериментах Хелбинга разыгрывались различные варианты этой ситуации. Пиплоиды в помещениях с одним и очень узким выходом в одной из стен неожиданно подвергались грозной «опасности», которая надвигалась от противоположной стены. Под опасностью мог подразумеваться пожар, скорость распространения которого была настолько мала, что при спокойном поведении, двигаясь с постоянной скоростью менее 1,2 м/с, все пиплоиды могли бы покинуть помещение через дверь, выбираясь по одному, что и происходило в экспериментах. Если же скорость движения пиплоидов превышала эту величину, ситуация принципиально изменялась — у двери скапливалось слишком много особей, создающих плотную толпу, в которой силы трения почти лишали их всякой подвижности. Модель наглядно демонстрировала многие особенности панического поведения больших масс людей (рис. 6.10, а).

Кстати, эффект закупорки выхода при давке имеет много бытовых аналогий, вспомните, как трудно бывает вытряхнуть соль из солонки, хотя размер всех крупинок заведомо меньше диаметра отверстий. Иногда отдельным пиплоидам и их ближайшему окружению удается преодолеть скопление и проскочить через дверь наружу, но затем толчея возобновляется, в результате чего через дверь спорадически вырываются только малые группы, а процесс эвакуации из помещения становится крайне неэффективным.

Таким образом, несмотря на то что каждый пиплоид «запрограммирован» двигаться как можно быстрее, скорость коллективного движения заметно замедляется, причем «заторможенное», паническое состояние возникает почти сразу после того, как индивидуальная личная скорость пиплоидов превышает некоторое критическое значение (в описываемых экспериментах • 1,5 м/с). Ниже этого порога ускорение пиплоидов только способствует более быстрой эвакуации из помещения, однако выше — любое дальнейше ускорение неизбежно ведет к замедлению общего процесса (рис. 6.10, б Быстрота движения частиц системы оборачивается замедленностью дейс твий системы в целом, что вновь указывает на некий неравновесный фазовы переход, в данном случае от спокойного состояния к паническому.

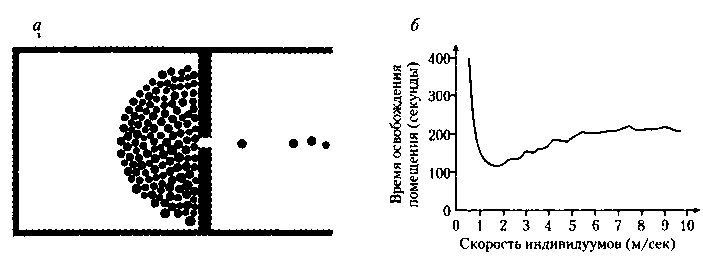
Рис. 6.10. (а) Моделирование процессов бегства толпы из заполненного помещ< ния. При очень высокой скорости движения все люди немедленно скапливаются единственной двери, устраивая давку и мешая друг другу покинуть помещение, чт соответствует паническому состоянию толпы, (6) Время, необходимое для эвакуаци людей из помещения, при повышении скорости передвижения отдельных инд* видов сперва уменьшается, но затем, после превышения некоторого критическоі значения скорости, начинает возрастать, сигнализируя о наступлении паническоі состояния, когда люди начинают мешать друг другу. С методами и результатам моделирования можно ознакомиться на сайте «Pedestrian simulations» по адрес angel.elte.hu/-panic/.

При дальнейшем росте скорости частиц (до ~ 5 м/с) в модель дополна тельно вводилась упоминавшаяся вероятность травмы пиплоида из-за повь шения давления в толпе[64], причем число травм возрастает со скоростью, та что для реальной толпы в целом повышение скорости движения отдельны людей означает не только замедление скорости эвакуации, но и нарастани опасности получения травм.

Говоря о реальных условиях спасения при массовой панике, следует осс бо отметить, что в заведениях типа ночных клубов обычно царит полутьм; при появлении следов дыма видимость уменьшается до метра-полутор; что не позволяет посетителям определить правильное направление бегств; Хелбинг и его коллеги попытались смоделировать поведение толпы в эти специфических условиях. Они исходили из того, что при возникновени серьезной угрозы любой человек инстинктивно начинает лихорадочны (но вполне осознанные) поиски выхода, однако именно наличие други людей в ближайшем окружении серьезно осложняет решение этой задачі

Действительно, увидев нескольких людей, бегущих в определенном направлении, любой из нас вполне резонно посчитает, что они знают правильное направление, — в сущности, именно такая естественная реакция и является основой группового поведения. Исследователи скомбинировали поведение пиплоидов в момент опасности из разных компонентов поведения: индивидуального (случайный, но целенаправленный поиск) и стадного (коллективное поведение).

Как показало моделирование, объединение в малые группы является очень правильной реакцией на опасность и сразу повышает шансы группы на выживание, поскольку каждый член группы может тут же воспользоваться выходом, обнаруженным любым другим членом группы. Однако стадное поведение обладает тем, что физики называют эффектом самоусиления, когда большая группа автоматически привлекает все большее число участников из окружения, и именно в этом скрывается серьезная опасность для всех. В своих модельных экспериментах Хелбинг показал, что все в толпе ищут один выход и забывают о возможности поиска других выходов даже в тех случаях, когда заранее известно о существовании таких альтернативных выходов. Воздействие эффекта стадности учитывалось по описанной ранее методике Вицека для самодвижущихся бактерий, взаимодействующих друг с другом, т.е. каждый пиплоид старался совместить направление своего движения с усредненным направлением движения своего ближайшего окружения.

В модельном эксперименте пиплоиды располагались в помещении с несколькими невидимыми им выходами, после чего в системе «создавалась» опасность, и они начинали искать выходы при различных уровнях коллективного взаимодействия. Оказалось, что при усилении стадного эффекта (что вообще характерно для реальных ситуаций панического поведения толпы) процесс развивается довольно сложно. Сначала при небольшом усилении стадного взаимодействия поиск выходов действительно становился более эффективным за счет того, что разные группы пиплоидов начинали обнаруживать разные выходы и пользоваться ими, однако при дальнейшем повышении уровня «стадности» все сильнее проявлялся обратный эффект, заключающийся в том, что образующиеся очень большие группы бросались к обнаруженным выходам, прекращая поиски остальных. Естественно, при этом возникали свалка и давка, в то время как другие выходы оставались свободными. Существует некий средний уровень стадности, обеспечивающий оптимальное поведение массы людей, а любые отклонения от него ухудшают ситуацию.

Этот результат может быть практически использован при проектировании систем эвакуации людей из крупных объектов и помещений. Обычно при расчете пропускной способности входов и выходов планировщики несколько простодушно исходят из того, что люди покидают помещения равномерно через все выходы, подобно тому как вода вытекает из всех отверстий решета. Хелбинг считает такой подход ошибочным, поскольку в реальных ситуациях толпа ведет себя нерационально.

Рис. 6.11. Машина «Скорой помощи», пытающаяся пробиться через толпу участ ников лондонского карнавала в Ноттинг-Хилле (2001 год).

Возглавляемая Майклом Батти группа провела собственные исследования пытаясь выработать на основе компьютерных моделей меры по предотвращении опасных и неконтролируемых перемещений больших человеческих масс. В ка честве объекта исследования было выбрано поведение толпы на двухдневно[65] карнавале в Ноттинг-Хилле в северной части Лондона, где ежегодно на очен: небольшом участке (около одной квадратной мили) собирается более милли она человек. Обеспечение безопасности этого популярного мероприятия давн< стало головной болью для мэрии Лондона и полиции, достаточно напомниті что в 2001 году пострадали более пятисот человек, около ста были госпитали зированы. При этом серьезной проблемой является даже использование машиі «Скорой помощи» в условиях столь массового сборища (рис. 6.11).

Модель, созданная М.Батти, основывалась на тенденции пешеходо: объединяться в группы и толпы, создающие массовые потоки людей меж ду центрами различных мероприятий и аттракционами карнавала. Во они располагаются в Ноттинг-Хилле по большому кругу, вдоль которог размещены 38 крупных пунктов входа и выхода, среди них главные — пят станций метрополитена. Исследователи пытались выработать такие мері контроля потоков (барьеры, перекрытия улиц, ограждения и т. п.), которы позволили бы минимизировать риск образования перенасыщенных тол на главных точках проведения мероприятий карнавала, расположенны вдоль главного круга*. Следует особо подчеркнуть, что полиция, поли тические деятели и Комитет по проведению карнавала, подчиняющийся Совету Большого Лондона, очень высоко оценили полученные результаты, позволяющие им по-новому оценивать и избегать опасностей, которые постоянно возникают при проведении этих крупномасштабных мероприятий. Компьютерное моделирование позволило выбирать альтернативные меры регулирования поведения толпы, не превращая каждый раз огромное и очень популярное мероприятие в гигантский и опасный социологический эксперимент.

Полученные командой Батти результаты показали, что такой тип моделирования перспективен для регулирования городских систем. Он писал по этому поводу следующее: «Раньше все почему-то невольно исходили из предположения, что города могут быть моделированы как некие квазиестест- венные образования, в которых регулирование может осуществляться только постфактум»¹¹. Действительно, мероприятия типа и масштаба карнавала в Ноттинг-Хилле с самого начала увязаны со многими ограничениями — общей планировкой маршрутов, размещением пропускных пунктов и т.д., однако ничто из этого не является жестко заданным: маршруты могут быть как-то изменены, некоторые пропускные пункты закрыты и т.д. Понимание механизмов поведения толпы значительно расширяет возможности планирования мероприятий, объединяя, по словам исследователей, предвидения с предписаниями. Организация движения становится более гибкой, возникает возможность непрерывного учета параметров ситуации, процесс управления приобретает итерационный (как говорят математики) и интерактивный характер. Еще раз подчеркнем, что моделирование движения пешеходов не столько диктует людям новые правила, сколько рекомендует более рациональную систему организации этого движения, основанную на более точной оценке того, что люди будут делать в той или иной ситуации. В этом проявляется подлинная сущность современной социальной физики.

Ученые пока только приступают к серьезному изучению законов движения человеческих потоков, однако даже первые результаты убедительно свидетельствуют о том, что сложность человеческого поведения не превышает нашей способности к пониманию и предвидению по крайней мере некоторых его важных аспектов. Возможно, один из интереснейших новых результатов заключается в том, что резкие изменения в массовом поведении могут возникать спонтанно, а не только вследствие согласованных или намеренных действий конкретных лиц. Однако подход в целом таит в себе и некоторые «ловушки» для будущих исследователей. Парриш и Эделыитейн- Кешет предупреждают об опасности чрезмерного увлечения теоретическими моделями групповой динамики живых существ: «Существует много наборов правил, создающих в модели групповое поведение, напоминающее некоторые реальные жизненные процессы и формы, однако следует помнить, что эти результаты, при всей их наглядности и привлекательности, могут оказаться просто неинформативными и бесполезными, если исследователи не смогут вывести поведение индивида из возникающих свойств группы»¹².

Другими словами, тот факт, что модель демонстрирует правдоподобно' коллективное поведение системы, еще не означает правильности исходны: предпосылок, что, в свою очередь, не гарантирует правильности предсказа ний для других обстоятельств. Удачно подобранные для модели «социальны» силы» могут оказаться эффективными в более широком диапазоне условий чем предполагали их создатели, однако столь же убедительными могу' оказаться и результаты, полученные с использованием других моделей і т.д. Все эти замечания свидетельствуют лишь о том, что методика и теори; описываемых исследований находятся в процессе становления.