СЛУЧАЙНЫЕ БЛУЖДАНИЯ

Обнаружение хаоса в экономических циклах обычно приписывают Ирвингу Фишеру, но в действительности честь его открытия принадлежит французскому математику Луи Башелье, который еще в 1900 году обратил вниманйе на то, что цены на товары и акции флуктуируют. Именно он показал, что в основе рыночной экономики лежат некие случайные процессы, но его имя практически не упоминается в учебниках экономики, поскольку Башелье был вовсе не экономистом, а физиком и учеником великого математика Анри Пуанкаре в Высшей политехнической школе. В докторской диссертации Башелье с необычным для математики названием «Теория спекуляций» предлагалась экономическая модель, основанная на чисто физических принципах и идеях. Его коллегам и современникам такой подход показался настолько необычным и даже странным, что работа осталась почти незамеченной и не была воспринята всерьез ни математиками, ни экономистами.

Между тем выдвинутые в диссертации Башелье идеи просто значительно опередили свое время. В попытке создать математическое описание случайных флуктуаций он даже попутно решил чрезвычайно важную для физики задачу о так называемых случайных блужданиях частицы. При этом Башелье на пять лет опередил самого Альберта Эйнштейна, прославившегося среди прочего решением именно задачи о броуновском движении, о чем рассказывалось в гл. 2. Направление движения частицы при случайных блужданиях меняется непредсказуемым образом, и Башелье предположил, что точно таким же образом меняется биржевой курс акций, т.е. ввел флуктуации в качестве «шума». В гл. 2 уже отмечалось, что такой случайный фон является мерой хаотичного движения, а его амплитуда соответствует температуре системы. Другими словами, существует характеристический «масштаб» случайных смещений частицы или других отклонений ее усредненных параметров.

Сейчас математики имеют хорошо разработанную методику изучения случайных блужданий, основанную на статистическом подходе. Действительно, тот факт, что никто не может предсказать точное направление движения в заданный момент времени, как уже ясно из предыдущего материала книги, вовсе не означает отсутствие всякого описания. Например, если бы мы могли нанести на отдельную частицу метку и проследить за ней достаточно долгое время, мы могли бы получить некий паттерн поведения, позволяющий построить, например, зависимость частоты появления флуктуации от ее размера.

Читатель наверняка не удивится тому, что такие расчеты вновь приводят нас к уже знакомой колоколообразной кривой Муавра, которую когда-то Адольф Кетле охарактеризовал как скрытое проявление «закономерности» в социальной статистике, а математики просто называют распределением Гаусса. Со времени первых статистиков XIX века уже известно, что любые параметры со случайно изменяющейся величиной должны иметь именно такое распределение. Исходя из того, что практически все относящиеся к социальным наукам величины подчиняются гауссовской статистике, Башелье вполне разумно предположил, что и цены на бирже колеблются в этом режиме. Его целью было введение элемента случайности в экономическую модель, и эта цель была блестяще достигнута. Подчеркнем, что Башелье не задавался вопросом о происхождении самих флуктуаций, а лишь постулировал, что они имеют конкретное распределение.

Сто лет назад концепции шума и флуктуаций казались экзотикой даже самим физикам, так что не стоит упрекать современников за невнимание к работе Башелье. Большинство ученых тогда интересовались лишь тем, что происходит с системами при нарушениях, значительно превышающих уровень фонового шума. Говоря проще, физиков интересовало только то, с какой средней силой газ давит на стенку, а не мелкие колебания этого давления в ничтожные промежутки времени из-за незначительных неоднородностей в плотности газа. Кроме этого, нельзя забывать, что и экспериментальная техника того времени не позволяла осуществлять столь тонкие измерения, чего Максвелл и не скрывал при создании своей кинетической теории.

Сегодня понятия шума и флуктуаций являются одними из важнейших в статистической физике. При этом очень важно, что в физических системах шум не всегда подчиняется статистике Гаусса. Как выяснили физики, на некотором уровне «дикости» и непредсказуемости процессов они перестают быть гауссовскими, так что, строі;о говоря, если бы Башелье измерял колебания цен с очень высокой точностью, он был бы разочарован. Мы же, зная, где и что надо искать, можем это увидеть со всей ясностью.

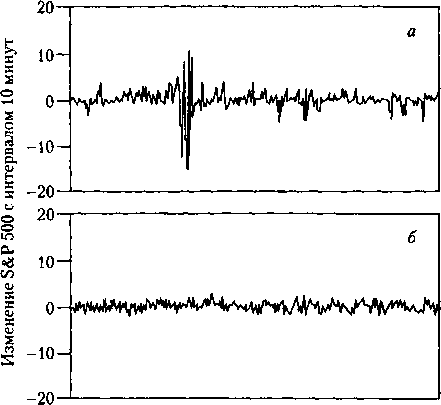
Рис. 8.2: а) колебания индекса цен S&P 500 (Standard & Poor 500 market index), одного из основных показателей состояния экономики США. Величина изменений в данном случае соответствует разнице цен, возникающей на бирже за интервал времени 10 минут. Т. е. нулевое значение означает, что индекс не изменился за последние 10 минут; 6) на нижнем рисунке представлена модельная картина чисто гауссовских флуктуаций, значительно отличающихся от реального изменения курса стоимости товаров и акций.

На рис. 8.2, а приведена типичная кривая флуктуаций стоимости (курса) акций на бирже в зависимости от времени. Для сравнения там же (рис. 8.2, б) приводятся колебания, соответствующие чисто гауссовскому шуму. Очевидно, что колебания биржевых цен не подчиняются статистике Гаусса, причем отличие состоит в том, что реальные цены временами испытывают очень резкие колебания, значительно превосходящие пределы значения по нормальной кривой распределения. Последние имеют типичную «шкалу», равную ширине полосы пиков, для реальных данных такую закономерность выделить нельзя.

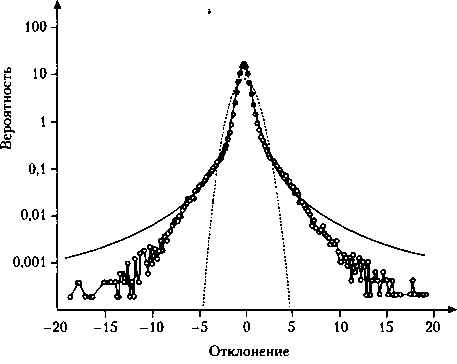
Рис. 8.3. Распределение вероятностей для индекса S&P 500 с временным интервалом в 1 минуту (в отличие от рис. 8.2, а, где интервал составляет 10 минут), но форма кривой сохраняется при изменении интервала по крайней мере до дней. Пунктиром показано гауссовское распределение[78] Сплошная линия соответствует распределению вероятностей для описанного ниже механизма «полетов» Леви.

Еще один вариант выявления разницы наблюдаемых закономерностей с классической статистикой состоит в построении графика зависимости вероятности отклонений от их величины (рис. 8.3.). Легко заметить, что даже при небольших отклонениях реальные данные плохо соответствуют гауссовскому распределению. Еще более отчетливо различия проявляются при больших отклонениях от среднего, которые гауссовское распределение рассматривает как крайне маловероятные. В гауссовской модели Башелье большие флуктуации в цене, соответствующие биржевому краху или неожиданному буму, представлялись невозможными в принципе, а рынок должен был колебаться вокруг более или менее устойчивого состояния. Но крахи тем не менее случаются.

Такие «экстремальные» события описываются на жаргоне физиков «хвостами» функций распределения, т.е. участками распределений, соответствующими почти нулевым вероятностям. На первый взгляд может показаться, что о таких особых флуктуациях можно и не беспокоиться, поскольку подавляющее большинство флуктуаций весьма хорошо согласуется с гауссовским распределением, а отклонения от него относятся лишь к чрезвычайно редким событиям. Однако проблема состоит в том, что именно эти сверхредкие флуктуации особенно волнуют экономистов, ведь речь идет о финансовых крахах. Экономист, пренебрегающий редкими, но исключительно опасными ситуациями, напоминал бы инженера, который создает гидротехническую систему, исходя только из среднего значения уровня в реке и не учитывая редких, но очень опасных паводков и наводнений. При этом стоит отметить, что отклонения от нормального распределения не были непосредственно зарегистрированы во время довольно серьезных потрясений биржи в 1987 и 1997 годах. Даже средние по величине отклонения вполне вписывались при этом в гауссовское распределение. Все дело в том, что поведение рынка не является случайным!