Во что превратились звуковые волны

Итак, мы уже поняли, что солитоны перемещаются со скоростями, меньшими v₀. А как же с обычными звуковыми волнами — могут ли они распространяться в среде, смоделированной Френкелем и Конторовой?

Возвратимся к уравнению (6.2). Даже для волн очень малой амплитуды его правую часть отбросить нельзя. Можно только приближенно заменить ее на -2?f₀(y_n/?). Тогда сразу видно, что y_n(t) будет изменяться по синусоидальному закону, если величина «эффективной массы» m_• отрицательна. При положительной эффективной массе никаких колебаний y_n(t) не получится (вспомните гл. 4!). Предположим поэтому, что m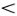_•  0. Тогда из формулы (6.3) следует, что скорость распространения волны v должна быть больше v₀, т. е. больше чем в свободной цепочке атомов! Не противоречит ли это только что сделанным вычислениям? Конечно, нет. Скорость v — это фазовая скорость волны, и мы сейчас увидим, что скорость группы волн оказывается всегда меньше v₀.

Итак, подставим в формулу (6.2) соотношение (6.3) и заменим sin [2? (y_n/?)] на 2? (y_n/?). Для у_n(t) получаем тогда уравнение малых (линейных) колебаний

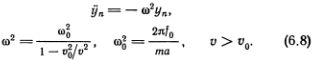
Решения этого уравнения, например

у_n(t) = у_n(t_n) соs [?(t - t_n)],

описывают, как и раньше, бегущие волны. Вспоминая рассуждения, приведенные при выводе формулы (6.5), представим волну смещения атомов в виде

у(t, х) = у₀ соs [?(t - x/v)].

Зависимость круговой частоты волны ? от фазовой скорости определяется формулой (6.8). Из условия связи длины волны с частотой и скоростью, т. е. из обычного соотношения ? = v/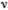 = 2?v/?, легко находим зависимость фазовой скорости от длины волны:

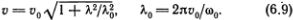
^{Упражнение: получите формулы (6.8), (6.9), воспользовавшись формулами (6.2), (6.3). Найдите групповую скорость и из формулы (5.23).}

^{О т в е т:}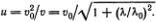

Зависимость скорости v от длины волны ? изображается хорошо изученной нами кривой — гиперболой. Обозначив v/v₀ = X и ?/?₀ = Y, можно записать уравнение (6.9) в более знакомом и приятном виде как Y² - Х² = 1. Как мы уже убедились в гл.4, точки этой кривой можно находить с помощью циркуля и линейки. Это построение выполнено на рис. 6.4, где

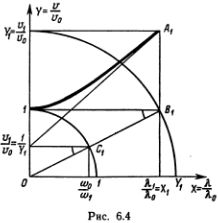
введены обозначения X₁ = ?₁/?₀ , Y₁ = v₁/v₀, 1/Y₁ = u₁/v₀, ?₁ — интересующее нас значение длины волны, v₁ — соответствующее значение фазовой скорости, определяемое формулой (6.9), а u₁ = v₀²/v₁ — значение групповой скорости.

^{Упражнение: выполните построение рис. 6.4. Покажите, что координаты точки А₁ подчиняются соотношению (6.9), координаты точки С₁ равны ?₀/?₁ и u₁/v₀ = v₀/v₁, где ?₁ — значение ?, соответствующее заданному значению ? = ?₁.}

Полученный нами закон дисперсии очень часто встречается в самых разных физических явлениях, и стоит потратить некоторое время, чтобы как следует понять его. Особенно полезно представить его с помощью дисперсионной формулы

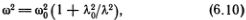
которая легко получается заменой в формуле (6.9) отношения v/v₀ на (??/?₀?₀).

Отсюда сразу видно замечательное свойство этого закона дисперсии — частота распространяющихся по цепочке волн всегда выше частоты ?₀, с которой колебался бы каждый атом цепочки вблизи своего положения равновесия, если бы он находился только под действием «подкладки». Физически очевидно, что частота ?₀ достигается при очень большой длине волны, когда соседние атомы смещаются без изменения относительно расстояния (как твердое тело). При этом пружины настолько слабо деформируются, что их как бы и нет.

Другое свойство закона дисперсии (6.9) роднит его с гравитационными волнами на глубокой воде. Мы видим, что фазовая скорость v(?) увеличивается с увеличением длины волны. Правда, эта зависимость несколько иная — скорость очень длинных волн на воде пропорциональна 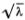, а скорость волн смещения пропорциональна ? (при ? 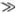?₀). Тем не менее можно считать, что природа прохождения дисперсии в обоих случаях качественно сходна. Во всяком случае, найденная нами дисперсия волн смещения в атомной цепочке не связана с ее дискретной структурой, которая может проявиться лишь при очень малых длинах волн, порядка постоянной решетки ?.

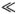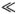При выводе закона дисперсии мы, в сущности, с самого начала пренебрегали дискретной структурой, предполагая, что ?  ? и ?  ?₀. Нетрудно проверить, что ?₀ = 2?l₀ (проверьте!). Поэтому при ?  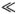?₀ будет также выполнено условие ?  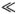l₀, т. е. размер дислокации l₀ должен быть большим по сравнению с межатомным расстоянием. Отсюда ясно, что дефект по Френкелю, размер которого примерно равен ?, нельзя описать с помощью изложенной здесь теории. Если, однако, не гнаться за точностью, то можно считать дефект по Френкелю просто дислокацией малого размера l₀, сравнимого с ?. Описание при этом будет качественно правильным.

^{Если это не вполне понятно, нужно вспомнить начало предыдущей главы, где описаны колебания системы из двух и трех грузиков, соединенных пружинками. Эти колебания соответствуют стоячим волнам сплошной резинки (рис. 5.4 и 5.5), но только нельзя рассматривать волны с длиной, меньшей 2?. Более точное описание дефекта по Френкелю можно найти с помощью исходного уравнения (6.1). Если пружины очень мягкие, т. е. если k? 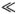 f₀, то существует равновесное состояние, в котором один из атомов смещен примерно на ?, а все остальные смещены мало (попробуйте это проверить самостоятельно!). Это и есть дефект по Френкелю.}

_{Раз уж мы вспомнили переход от цепочки атомов к сплошной среде, стоит написать, во что превратится при таком переходе основное уравнение (6.1). Как и при выводе уравнения Д'Аламбера, можно считать, что второй член в правой части перейдет в k?²y". Переходя от y(t, х) к ?(t, х) (вспомните вывод уравнений (6.4), (6.5), найдем в результате, что}

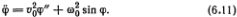
^{Если  ?₀ = 0, то из этого уравнения получается уравнение Д'Аламбера.}

^{К уравнению (6.11) приклеилось странное название — уравнение «синус-Гордона». Происхождение этого жаргонного наименования связано с тем, что при значениях ?, мало отличающихся от ?, т. е. ? = ? + ?, где 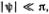оно переходит в уравнение}

^{Это, а если говорить совсем точно, несколько более общее уравнение было предложено в 1926 г. Э. Шрёдингером, О. Клейном, В. Гордоном и В. А. Фоком, и обычно физики для краткости называют его уравнением Клейна — Гордона. Подобное стремление к укорочению названий породило и сочетание «синус-Гордона».}

^{На самом деле уравнение (6.12) было известно уже в прошлом веке и называлось уравнением струны в упругой среде (действие упругой среды на каждый кусочек струны описывается членом 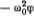 в правой части уравнения). Уравнение (6.11) также встречалось математикам в конце прошлого века. Оно появилось в связи с исследованиями по геометрии Лобачевского *) и было известно лишь геометрам. Достаточно полное изучение решений уравнения (6.11) было выполнено лишь в 1936 г. немецким математиком Р. Штойервальдом. Он нашел решения, соответствующие (на нашем с вами языке) одному солитону, двум солитонам и бризеру. Эти результаты до самого последнего времени были известны лишь немногим специалистам по геометрии и не оказали никакого влияния на развитие науки о солитонах. Для физики уравнение «синус-Гордона» было открыто Френкелем и Конторовой, и они же нашли его солитонное решение. Связать эти открытия с их именами естественно и справедливо, хотя наиболее удивительные свойства модели ФК были обнаружены позднее другими исследователями. Как сказал Больцман: «Еще почти никогда... не бывало, чтобы та самая голова, которая впервые натолкнулась на ту или иную новую идею, до конца исчерпала бы ее».}

^{*) Любому решению этого уравнения соответствует некоторая поверхность, на которой выполняются аксиомы геометрии Лобачевского. Такие реализации геометрии Лобачевского сыграли основную роль в признании его идей.}