Дисперсия волн в цепочке атомов

Связь дисперсии с атомной структурой проще всего понять в нашей пружинной модели. Хотя при этом речь идет о звуковых, а не о световых волнах, суть дела одна и та же. Эту мысль и развил Коши. Найдем вслед за ним дисперсионную формулу для волн в цепочке «атомов», соединенных пружинками. Вспомнив то, что мы знаем о связи дискретной цепочки со сплошным стержнем, попробуем сразу написать решение всех уравнений (5.8) в виде бегущей волны ():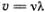

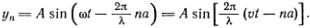
Если, как это делалось раньше, заменить n? на х и y_n(t) на y_n(t, х), то получится знакомая синусоидальная бегущая волна. Ее скорость v определяется из условия постоянства фазы (?t - 2?х/?). Поэтому скорость v называют фазовой скоростью. Если двигаться со скоростью v, то волна будет казаться неподвижной.

Так как 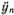= -?²y_n, то из (5.8) следует простое уравнение

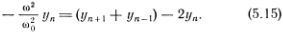
С помощью известной формулы для преобразования суммы синусов двух углов в произведение легко найти, что для синусоидальной волны y_n+1 + y_n-1 = .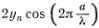

Подставляя это в уравнение (5.15), легко увидеть, что оно выполнено сразу для всех n, если

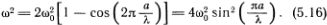
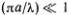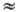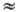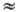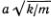Это и есть дисперсионная формула Коши. Если длина волны много больше расстояния между атомами, т. е. , то sin (??/?) ??/? и ?  2??₀(?/?). При этом дисперсия исчезает, так как скорость не зависит от ?: v (?) = ??/2? ??₀ = = v. Этот результат мы уже получили раньше при переходе к «непрерывному» пределу (см. формулу (5.14)). Если длина волны сравнима с расстоянием между атомами, то скорость зависит от ?:

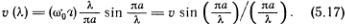
С уменьшением ? она уменьшается. Заметим, что нет смысла рассматривать длины волн, меньшие 2?. Понять это легко, если вспомнить, что наблюдать мы можем лишь движения частиц, а не мысленно проведенные через их отклонения синусоиды (см. рис. 5.5). С учетом этого ограничения скорость убывает при уменьшении длины волны от значения v до значения (2v/?).

Дисперсионную формулу (5.16) можно получить и из найденного нами раньше выражения для частот стоячих волн в цепочке конечной длины l (см. (5.9)). Для этого заметим, что длина волны в моде с номером М равна ?_М = 2(N + 1)?/М = 2l/М, где М = 1, ..., N. Дисперсии не было бы, если бы соответствующие частоты ?_М были пропорциональны М. Как мы знаем, такой пропорциональности для больших М нет. Отсюда и возникает зависимость скорости v от ? при малых длинах волн и больших частотах. Выражая правую часть формулы (5.9) через ?_М, получаем соотношение Коши (5.16) между ?_М и ?_М.

Плавные синусоидальные кривые, огибающие стоячие волны (5.7), можно получить, заменив в формуле (5.7) n? на х:

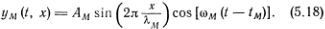
Это выражение описывает и стоячие волны в упругом стержне. При этом ?_М принимает значения ?_М = 2l/M, где M может неограниченно возрастать (М = 1, 2, 3, ...). Значения частот 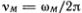получаются из дисперсионной формулы (5.16), если заменить в ней sin (??/?) на ??/? (вспомните, что в пределе непрерывной среды ? ? 0):

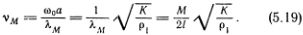
Аналогичные формулы читатель легко напишет для частот собственных колебаний струн, воздуха в органных трубах и т. д.