Взаимодействие дислокаций

Без достаточно сложных математических расчетов невозможно понять, что будет происходить с двумя дислокациями, сталкивающимися друг с другом. Точное решение уравнений показывает, что одноименные дислокации взаимодействуют точно так же, как солитоны Рассела, т. е. подобно сталкивающимся мячам (см. рис. 2.4). Попробуем если и не понять, то хотя бы описать, что происходит, когда на покоящуюся антидислокацию налетает другая антидислокация. Обе дислокации во время «соударения» несколько деформируются. За время их соприкосновения кинетическая энергия налетевшей дислокации перейдет к первоначально покоившейся, которая и начнет двигаться вперед, сохраняя свою форму. В общем, можно сказать, что дислокация подобна мячу. Главное здесь то, что дислокация сохраняет форму. Ее легче сдвинуть, чем деформировать.

^{На самом деле, как мы скоро увидим, дислокация не деформируется лишь при малой скорости ее движения, много меньшей скорости распространения продольной звуковой волны по цепочке атомов. В общем случае все продольные (по оси, соответствующей направлению движения) размеры дислокации уменьшаются, т. e. 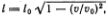где v — скорость дислокации, v₀ — скорость распространения звука. Зависимость энергии движущейся дислокации от скорости дается формулой 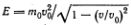. Как формула для размеров дислокации, так и формула для энергии аналогичны соответствующим формулам специальной теории относительности *). C учетом всего, что мы узнали о дислокациях, можно сказать, что дислокация подобна элементарной частице. В довершение этой поразительной аналогии, имеются еще и «античастицы» — антидислокации.}

^{*) Нелишне подчеркнуть, что эта аналогия чисто математическая. В теории относительности написанные формулы имеют совершенно другой физический смысл. К тому же, для реальных дислокаций они выполняются лишь приближенно.}

Как же происходит столкновение дислокации с антидислокацией? Когда антидислокация (антисолитон)  налетает слева на покоящуюся дислокацию D (солитон), то сжатые в пружины распрямляются, из в D пробегает волна сжатия, которая превращает D в , и наоборот. Все эти события происходят очень быстро, так как передача энергии от к D и распространение волны сжатия, превращающей D в и в D, происходят со скоростью звука. Если начальная скорость налетающего солитона намного меньше скорости звука, то оба солитона не успеют заметно изменить свою форму и разлетятся, как мячи. В результате налетевший антисолитон превратился в солитон D и остановился несколько левее положения первоначально покоившегося солитона D. Тот, в свою очередь, превратился в антисолитон и летит направо, занимая положение немного правее того, которое занимал бы налетающий антисолитон, если бы не было столкновения. Таким образом, мы совершенно ясно видим, что ничего похожего на прохождение одного солитона «сквозь другой» не происходит. Только на первый взгляд может показаться, что солитоны ведут себя как импульсы в струне, движение которых мы изучали в гл. 5.

На примере дислокации особенно ясно видно, что солитон подобен частице. Его движение при слабом взаимодействии с другими солитонами, в основном, определяется законами механики. Нужно только учитывать, что солитоны способны при этом деформироваться и «перекрашиваться» — «положительный герой», сталкиваясь с «отрицательным», сам становится «отрицательным», и наоборот.

До сих пор слова «положительная» и «отрицательная» дислокации были просто некоторыми фигуральными выражениями. Замечательно, что им можно придать буквальный смысл, приписав дислокациям соответствующие заряды. В положительной дислокации общий эффект смещения атомов такой же, как при образовании дырки. Если бы атомы нижнего неподвижного ряда были электрически заряжены положительно, а верхнего отрицательно, то дислокация, как и дырка, переносила бы положительный электрический заряд. Независимо от того, заряжены или не заряжены атомы, припишем дислокации (как и дырке) заряд +1. Тогда антидислокации надо приписать заряд -1. Если есть несколько дислокаций и антидислокаций, то алгебраическая сумма их зарядов будет сохраняться, что бы с ними ни происходило (докажите это утверждение!). Конечно, выбор для зарядов дислокаций значений +1 — дело соглашения. Ясно также, что сравнивать заряды дислокаций можно лишь в одной и той же решетке. В отличие от настоящих частиц, дислокации не существуют вне породившей их среды, и понятие заряда имеет смысл лишь для определенной, заданной решетки.

Читатель, несомненно, уже уловил, куда завело нас исследование совсем простой модели. У нас есть частицы и античастицы, которые могут порождаться и уничтожаться парами. Есть сохраняющиеся заряды, причем одноименные заряды отталкиваются, а разноименные притягиваются. Есть и нечто похожее на электромагнитные волны. Это, как вы уже, конечно, догадались, бегущие волны с малой амплитудой колебаний грузиков, когда грузики колеблются вблизи своих положений равновесия. Иначе говоря, это просто звуковые волны *), распространяющиеся в нашей «среде» из грузиков и пружин.

_{*) В отличие от обычных звуковых волн, эти волны сильно диспергируют при больших значениях ?. Как и для волн на глубокой воде, их фазовая скорость v растет с ростом ?. Позже мы получим соответствующую дисперсионную формулу, а пока этим отличием можно пренебречь.}

В общем, мы создали целый мир. Конечно, это довольно простой мир. Трудно себе представить, чтобы из таких элементарных частиц могли бы возникнуть, скажем, мыслящие существа. Одномерность этого «мира» сильно ограничивает возможности образования достаточно сложных структур (не случайно мы с вами трехмерны!). Тем не менее не нужно и недооценивать возможности этой простой модели. В конце этой книги мы познакомимся с некоторыми идеями применения подобных одномерных систем, а в следующем разделе увидим, что даже в самом простом «мире» может существовать очень своеобразный «атом», построенный из дислокации и антидислокации.