Малые колебания маятника
Чтобы подступиться к решению нелегкой задачи о движениях маятника, рассмотрим сначала малые колебания, когда угол настолько мал, что можно положить sin ? 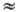 ?. Уравнение теперь становится линейным (это и есть линеаризация!):
?. Уравнение теперь становится линейным (это и есть линеаризация!):

, и можно угадать (или вспомнить!) его решение ? = ?M(?0t) *), которое равно нулю при t = 0. Благодаря линейности уравнения максимальное значение угла ?M формально может быть произвольным числом, но мы, конечно, должны помнить, что при больших значениях ?M наше приближение не годится. Поэтому число ?M должно быть таким, что sin ?M 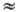 ?M.
?M.
*) для этого достаточно вспомнить правило дифференцирования тригонометрических функций. Ниже это движение будет построено другим, геометрическим способом.
Этим решением, разумеется, не исчерпывается все множество решений. Мы заранее предположили, что ?(0) = 0, и этим отбросили, например, решение ? = cos (?0t), которое тоже легко угадать. Пользуясь линейностью, теперь можно найти и общее решение, складывая sin (?0t) и cos (?0t), умноженные на произвольные амплитуды. Ясно, что этим способом получается любое колебание, так как первое решение позволяет получить любое значение скорости в начальный момент, а второе — задать любое начальное положение.
Самое общее малое колебание можно получить и другим способом, понимание которого очень полезно. Заметим, что движение ? = ?Msin(?0t) можно наблюдать, пустив другие часы отсчитывать время в момент t0 (по старым часам). При новом отсчете времени то же самое движение будет выглядеть как ? = ?Msin[?0(t + t0)].
Нетрудно проверить, что это решение при любых t0 удовлетворяет уравнению 4.1. Отсюда следует, что если движение ? = ?Msin(?0t) возможно, то и движение ? = ?Msin[?0(t + t0)] также возможно. А это движение уже самое общее, поскольку подбором ?M и t0 можно задать любые начальные значения скорости и положения.
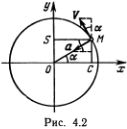
Решение уравнения для малых колебаний можно найти совсем простым способом. Достаточно вспомнить геометрическое определение тригонометрических функций и закон движения материальной точки по окружности. Пусть точка М движется по окружности единичного радиуса с постоянной скоростью V = ?0 (рис. 4.2). Скорость V направлена по касательной, и ее проекция на ось Оу равна ?0cos ?, где ? = ?0t (радиан). Точка S совершает гармоническое движение, длина отрезка (OS) = sin ?0t, и ее скорость v равна проекции скорости V на ось Оу, т. е. v = ?0cos(?0t). Полное ускорение ? направлено к центру и равно 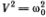 (радиус окружности равен 1). Ускорение точки S равно проекции ускорения а на ось Оу, т. е.
(радиус окружности равен 1). Ускорение точки S равно проекции ускорения а на ось Оу, т. е. 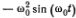 . Таким образом, ускорение точки S равно
. Таким образом, ускорение точки S равно 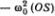 . Если взять (OS) = ?, получим ?" =
. Если взять (OS) = ?, получим ?" = 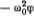 . Обозначив
. Обозначив 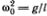 , находим, что ? = sin(?0t) есть решение линейного уравнения для малых колебаний маятника. Заодно вспомним, что период колебаний Т совпадает с временем полного оборота точки М по окружности, т. е. равен
, находим, что ? = sin(?0t) есть решение линейного уравнения для малых колебаний маятника. Заодно вспомним, что период колебаний Т совпадает с временем полного оборота точки М по окружности, т. е. равен 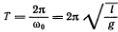 .
.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК