Реабилитация уединенной волны

Я гимны прежние пою...

А. С. Пушкин.

Еще при жизни Рассела ученые молодого поколения Жозеф Валентин де Буссинеск (1842—1929) и его сверстник лорд Рэлей, учившийся, между прочим, у Стокса, сумели найти приближенное математическое описание формы и скорости уединенной волны на мелкой воде. Позже появились еще две-три математические работы об уединенной волне, а также были повторены и подтверждены опыты Рассела. Казалось, все стало ясно. Тем не менее споры о существовании уединенной волны в узком кругу специалистов не прекращались — слишком велик был авторитет Эри и Стокса.

Наибольшую ясность в эту проблему внесли голландские ученые Дидерик Иоханнес Kортевег (1848—1941) и его ученик Густав де Фриз, которые в 1895 г. нашли уравнение, наиболее точно описывающее основные эффекты, наблюдавшиеся Расселом. Обобщив метод Рэлея, они получили довольно простое уравнение для волн на мелкой воде и нашли его периодические волновые решения. Эти волны, как и волны Герстнера, имеют несинусоидальную форму и становятся приближенно синусоидальными, только если их амплитуда очень мала (рис. 2.2, а). При увеличении длины волны они приобретают вид далеко отодвинутых друг от друга горбиков (рис. 2.2, б), а при очень большой длине волны (в пределе, бесконечно большой) остается один горбик, который и соответствует уединенной волне (рис. 2.2, в).

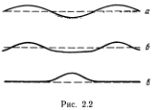
Волны, изображенные на рис. 2.2 б, можно наблюдать на отмелях, пока их вершинка не начинает деформироваться и они не опрокидываются. Форму волн Кортевега и де Фриза нельзя описать так просто, как форму волны Герстнера, ее можно представить только с помощью так называемых эллиптических функций, открытых Абелем и изученных другими выдающимися математиками, в особенности Карлом Якоби (1804—1851), братом известного петербургского академика Бориса Семеновича Якоби (1801—1874).

Уравнение Кортевега — де Фриза называют теперь КдФ-уравнением, и ему суждено было сыграть большую роль во втором рождении солитона в наше время. Для физиков оно важно тем, что с его помощью можно описывать не только волны на мелкой воде, но и многие другие волны. Для математиков оно послужило стартовой площадкой при построении глубокой и важной математической теории. Для «собственно математиков» история солитона начинается с КдФ-уравнения. Не забудем, однако, что они в свое время не сумели разглядеть глубин, таящихся в уравнении мелкой воды, и основательно забытая работа Кортевега и де Фриза вернулась к новой жизни лишь через 70 лет в основном усилиями физиков. Авторы не подозревали, конечно, о судьбе, уготованной их уравнению. Они просто честно разобрались в том, что сделали до них другие, выяснили, кто прав, кто неправ и почему, и изложили все так, чтобы каждый, кто обратится к этой проблеме, мог бы разобраться в сути дела и в вычислениях. Короче говоря, они сделали все, что могли, но тем не менее и после этого уединенная волна... ушла в уединение дальних углов научных библиотек.

Может быть, и сами авторы не придавали большого значения своей работе. Кортевег прожил долгую жизнь и был известным ученым (почти сорок лет Кортевег занимал кафедру математики Амстердамского университета), однако о его, с нашей точки зрения, главной работе почти никто не вспоминал при его жизни, и она не упоминается в его посмертной биографии (1945 г.). Де Фриз был преподавателем гимназии, членом Голландского математического общества. После защиты диссертации, составившей основу его статьи с Кортевегом, он в 1896 и 1897 гг. опубликовал две статьи о циклонах. Больше о нем пока ничего не известно. По-видимому, де Фриз, как и Кортевег, к исследованию волн больше никогда не возвращался.

Изредка новые поколения ученых, занимавшихся проблемами гидродинамики, возвращались к обсуждению КдФ-уравнения и уединенных волн. Такие вспышки интереса наблюдались около 1925 г. и после 1945 г. В 1946 г. Михаил Алексеевич Лаврентьев (1900—1980) дал первое математически строгое доказательство существования уединенной волны. Это доказательство было очень сложным, более простое нашел американский математик Курт Фридрихе в 1954 г. Примерно в то же время были проделаны тщательные опыты с уединенными волнами, в которых использовалась киносъемка. Эти достижения оставались известными лишь узкому кругу специалистов.