Возвращение солитона Рассела
И долго ждал ты час,
назначенный судьбой...
В. Брюсов
Вы, конечно, помните, что Кортевег и де Фриз получили свое уравнение при попытке найти точное математическое описание солитона Рассела с небольшой амплитудой. Теперь выясняется, что то же самое уравнение может описывать совершенно другие физические явления. Это, конечно, не случайно. Уравнение КдФ годится для математического описания самых разных нелинейных волн. На самом деле это простейшее уравнение для любых слабо нелинейных и слабо диспергирующих волн.
Если оба эти эффекта (нелинейность и дисперсия) настолько малы, что ими можно пренебречь, то уравнение КдФ описывает волны произвольной формы, бегущие в одном направлении. Иными словами, форма волны y (t, х) задается произвольной функцией у (t, х) = f (x - v0t). Для волн на мелкой воде v0 =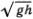 
, где h — глубина. Напомним, что воду можно считать мелкой, если минимальная длина синусоидальных волн (?), входящих в разложение Фурье функции f, во много раз превышает глубину h. Чтобы не думать о разложении Фурье, можно просто считать, что волна имеет синусоидальную форму.
Если теперь допустить, что имеется малая дисперсия, т. е. что фазовая скорость v синусоидальной волны немного зависит от ?, то простейшая зависимость будет иметь вид (ср. с формулами (5.17), (5.21))
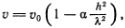
где ? — некоторое число, а v0 = 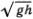. Для уравнения КдФ, описывающего волны на мелкой воде, ? = 2/3?2. Однако для волн в других средах значение ? будет другим, а величина h, имеющая размерность длины, будет иметь совсем иной смысл.
В гл. 5 мы уже сравнивали дисперсию длинных волн на мелкой воде и в цепочке упруго связанных атомов (формулы (5.21) и (5.17)) и убедились, что зависимость фазовой скорости от ? имеет при больших значениях ? один и тот же вид. Достаточно заменить h на 1/2?, где ? — расстояние между атомами, и из закона дисперсии волн на воде получится закон дисперсии длинных волн в цепочке атомов. Зная этот удивительный факт, совсем не трудно додуматься и до того, что в других физических системах закон дисперсии длинных волн может быть таким же. Однако такая мысль многие десятилетия никому не приходила в голову. Может быть, это произошло потому, что волнами на воде и в кристаллах интересовались разные исследователи, может быть, по другим причинам... Во всяком случае, ясная идея о существовании такого универсального закона дисперсии длинных волн сформировалась совсем недавно, уже в эпоху общего увлечения солитонами.
Чтобы теперь понять — как устроены волны КдФ, нужно ввести простейшую мыслимую нелинейность. Мы знаем, что скорость линейных диспергирующих волн не зависит от амплитуды, а зависит лишь от длины волны. Скорость же распространения нелинейных волн зависит и от амплитуды. Самая простая зависимость — линейная, когда рост скорости прямо пропорционален увеличению амплитуды. Именно она и реализуется для волн КдФ, а будучи самой простой, естественно, встречается и во многих других физических системах. Забуски и Крускал обнаружили, что такая нелинейность хорошо описывает нелинейные взаимодействия атомов в решетке. Еще раньше, в 1958 г., советский физик Р. З. Сагдеев подметил аналогию между некоторыми волнами в плазме и волнами на мелкой воде и показал, что в плазме также могут распространяться уединенные волны. Плазмой в это время уже занимались многие физики, и это наблюдение не осталось незамеченным. Вскоре удалось показать, что эти волны в плазме также можно описывать с помощью КдФ-уравнения. Это решило судьбу КдФ-уравнения, которое было извлечено из забвения и стало известно широкому кругу физиков и математиков. Знаменитым оно стало после того, как 3абуски и Крускал выяснили, что оно описывает солитоны, которые не изменяются после столкновения друг с другом, и что можно найти его самое общее решение. Это удалось в 1967 г. американским ученым Гарднеру, Грину, Крускалу и Миуре. От их работы обычно отсчитывают начало бурного развития науки о солитонах.
Выглядит уравнение КдФ совсем не страшно. Форма волны y (t, х) в момент времени t должна подчиняться соотношению
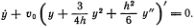
Здесь точкой обозначена производная по времени при фиксированном значении координаты х, а штрихом — производная по координате в заданный момент времени t. Если нарисовать зависимость профиля волны у от координаты, то этот график будет двигаться и деформироваться с течением времени. При этом у определяет наклон касательной к графику в точке х в момент t, а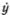 
— скорость движения точки графика у (t, х) по направлению оси у. Если в некоторый момент времени t нам известна зависимость у от х (в том числе и производные у', y'', у'''), то уравнение позволяет найти скорости 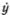всех точек графика, так что можно приближенно определить его вид в следующий момент t + ?t:
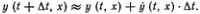
Решить такое уравнение — значит по начальному графику у (0, х) найти вид графика y (t, х) в любой последующий момент времени. Точное решение этой очень непростой математической задачи оказалось одним из наиболее замечательных достижений математики, которое стало возможным благодаря тесному и плодотворному сотрудничеству физиков, математиков и использованию ЭВМ.
Нетрудно понять, что КдФ-уравнение описывает лишь волны, распространяющиеся в одном направлении вдоль оси х. Заметим сначала, что эффекты дисперсии определяются членом 
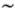у", а нелинейные эффекты — членом у2. Если ими пренебречь, то получится совсем простое уравнение 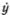+ v0y' = 0, которое мы обсуждали в гл. 5. Как оказалось, самое общее решение этого уравнения — любая функция от х - v0t, т. е. у (t, х) = f (х - v0t). Чтобы найти зависимость у от х в любой момент времени, достаточно нарисовать график функции у = f (х) и двигать его со скоростью v0 (v0 
0) в положительном направлении оси х. Чтобы описать волну, бегущую в противоположном направлении, нужно взять другой знак перед v0.
Как вы помните, уравнение Д'Аламбера не зависело от знака v0 и описывало волны, бегущие в обоих направлениях. Уравнение для дислокаций также обладало этим свойством. Почему же КдФ-уравнение не обладает этим свойством, в то время как волны на поверхности ручья от брошенного камня бегут в обоих направлениях *)?
*) Кортевег и де Фриз вывели свое уравнение из уравнения Буссинеска, которое больше похоже на уравнение Д'Аламбера и описывает волны, бегущие в обоих направлениях. Уравнение Буссинеска, однако, сложнее, чем КдФ-уравнение.
Ответ на этот вопрос на самом деле очень простой. Если нас не интересует начальный момент, когда от брошенного в ручей камня начинают разбегаться две волны, то мы можем отдельно изучать одну и другую. Если эффекты нелинейности и дисперсии достаточно малы, то обе волны убегут на большое расстояние друг от друга за столь малое время, что эти эффекты не успеют сказаться, и в дальнейшем можно следить за судьбой одной из волн, забыв о существовании другой. Именно поэтому можно описывать эволюцию обеих волн одинаковым по виду уравнением с разными знаками перед v0. (В случае дислокаций, когда эффекты нелинейности и дисперсии всегда велики, так поступить нельзя!)
Эта идея, в сущности очень простая, привела к огромному упрощению, которое позволило Кортевегy и де Фризу правильно понять природу солитона Рассела, а спустя 70 лет привело к созданию полной математической теории солитонов. С точки зрения физиков, теория солитонов на основе КдФ-уравнения кажется наиболее понятной, так как в ней наглядно видно, каким образом уравновешивание эффектов нелинейности и дисперсии приводит к образованию устойчивой уединенной волны. Мы больше не будем касаться математики солитонов, она достаточно сложна, а посмотрим на устройство солитона глазами физика.
Итак, если нет ни дисперсии, ни нелинейности, по поверхности могут распространяться импульсы любой формы, но это не солитоны. Всегда имеющиеся в физической системе малые эффекты дисперсии и трения вскоре исказят первоначальный импульс до неузнаваемости. Посмотрим, как влияет на него нелинейность. Заметим, что КдФ-уравнение с выброшенным последним членом, ответственным за дисперсию, можно решить точно. Метод решения был известен еще Лагранжу, однако его первые применения к реальным нелинейным волнам связаны с именем знаменитого немецкого математика Георга Фридриха Бернхарда Римана (1826—1866).
Пусть на поверхности воды образовался горбик, изображенный на рис. 7.4, кривая 1. Дальнейшая судьба этого горбика определяется тем, что скорость каждой точки графика зависит от ее высоты.
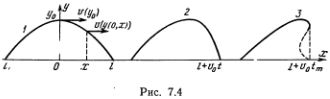
Для волн КдФ эта зависимость простейшая:
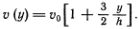
Быстрее всех движется вершина горбика. Ее скорость равна
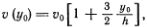
а скорость переднего фронта горбика, где у = 0, равна v0. Поэтому в некоторый следующий момент времени передняя часть горбика станет более крутой (кривая 2), а с течением времени произойдет «опрокидывание» волны (кривая 3), которое уже нельзя описать на этом простом языке. Такое опрокидывание волн все мы много раз видели, когда наблюдали прибой на берегу моря или на речной отмели.
А скалы кругом все отвесней,
А волны — круче и злей...
Г. Гейне
Не так легко, и притом небезопасно, наблюдать другое явление, вызванное описанным увеличением крутизны фронта волны. Если приливная волна из моря входит в устье реки, то может образоваться волна в виде высокой, крутой ступеньки (рис. 7.5), которую называют бором.
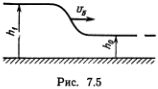
Бор — один из примеров ударной волны. Хорошо знакомый нам пример ударной волны — взрывной звук, который слышен, когда реактивный самолет проходит звуковой барьер. Более идиллический пример — щелчок пастушьего кнута.
Ударные волны были открыты Риманом в 1860 г. Он, однако, сомневался в возможности их наблюдения, в то время как Рассел уже заметил, что скорость распространения звука от пушечного выстрела больше, чем обычно измеряемая скорость звука в воздухе («звук пушечного выстрела доносится быстрее, чем команда открыть огонь»). Здесь Рассел действительно подметил одно из важных свойств ударной волны. Например, скорость движения бора равна vБ =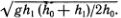 
Так как h1 h0, то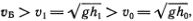 
и бор бежит быстрее, чем любая небольшая волна на поверхности воды с глубинами h0 или h1. Увеличение крутизны фронта волны и ее опрокидывание превращает гигантский, но безвредный океанский солитон в страшное стихийное бедствие — цунами.
Ударная волна в воздухе — очень сложное явление. На фронте ударной волны резким скачком возрастают давление, температура и плотность. Однако плотность не увеличивается выше определенного предела, тогда как давление и температура могут быть огромными. Например, при скачке давления в 100 атмосфер температура фронта волны достигает 3500 градусов. При такой температуре в молекулах возбуждаются сильные внутренние колебания и часть молекул кислорода даже распадается на атомы, возникают химические реакции. При более высокой температуре возникает очень сильное свечение. Апокалиптическое явление ударной волны (огненный шар «ярче тысячи солнц») печально известно из описаний ядерного взрыва, когда температура выше 10 000 градусов, а давление достигает 1000 атмосфер. Не дай нам Бог увидеть эту ударную волну!
Колоссальная ударная волна образовалась при падении знаменитого тунгусского метеорита (30 июня 1908 г.)*). Перед его падением в течение нескольких секунд был виден ослепительно яркий огненный шар, в момент падения раздался оглушительный взрыв, который слышали на расстоянии больше тысячи километров. Воздушная взрывная волна была зарегистрирована даже в Англии! По современным оценкам примерно такую волну вызывает ядерный взрыв в несколько Мегатонн. Однако тунгусская ударная волна не была вызвана ядерным взрывом. Она того же происхождения, что и ударные волны, возникающие при переходе самолетом «звукового барьера». Иными словами, она была вызвана движением небесного тела в атмосфере со сверхзвуковой скоростью. Может быть, это была комета или ее кусок.
*) В конце 40-x — начале 50-x годов лекции о «загадке Тунгусского метеорита» были столь же популярны, как и лекции на тему: «Есть ли жизнь на Марсе?»
Возникновением ударной волны объясняется свечение метеоров (болиды). Светящаяся ударная волна появляется и при торможении спутников в атмосфере. Кстати, в этом случае ударная волна очень полезна — кинетическая энергия спутника уходит на ее образование, и спутник тормозится — ударная волна работает, как парашют. В популярной брошюре А. С. Компанейца «Ударные волны» (М.: ГИФМЛ, 1963), по которой интересующийся читатель может получить более полное представление об ударных волнах, рассказано о случае чудесного спасения советского военного летчика в годы второй мировой войны. Его парашют не раскрылся, и гибель казалась неизбежной. Однако в последний момент как раз под ним взорвалась авиационная бомба. Ударная волна этого взрыва затормозила его падение и спасла жизнь.
К сожалению, большинство исследований ударных волн связано с современным оружием и, откровенно говоря, автору не хочется писать об этом. Вернемся лучше к нашим мирным солитонам.
Посмотрим теперь, как дисперсия вместе с нелинейностью приводят к образованию солитона. Наш первоначальный горбик (кривая 1, рис. 7.4) можно представить в виде суммы гармоник. Длина волны основной гармоники примерно равна удвоенной ширине горбика. Длины волн высших гармоник, сложение которых с основной приводит к образованию горбика конечной ширины, больше длины основной, а значит, они бегут вперед с большей скоростью. В результате увеличение крутизны переднего фронта, вызванное нелинейностью, смягчается, а при определенной форме и скорости горбика может полностью скомпенсироваться этим эффектом. Тогда-то и получается солитон. Если первоначальный горбик достаточно высокий, то он сначала может распасться на несколько горбиков, которые породят несколько солитонов. Если он очень низкий, то он просто расползется вследствие дисперсии.
Соотношение между эффектами дисперсии и нелинейности можно выразить с помощью простой формулы. Прежде чем написать ее, посмотрим на точное решение КдФ-уравнения, описывающее солитон,
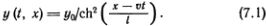
Здесь v = v0 [1 + (y0/2h)], а величина l определяется из соотношения
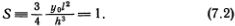
Это условие и выражает равновесие между эффектами нелинейности и дисперсии в солитоне. Хотя параметр S был известен уже Стоксу, его значение для теории солитонов было выяснено лишь в наше время.
Происхождение условия (7.2) можно понять, если вспомнить, что нелинейность увеличивает скорость движения вершины горбика на величину порядка v0y0/h, а дисперсия замедляет ее движение на величину порядка v0h2/l2 (напомним, что положение вершины горбика определяется основной гармоникой, длина волны которой примерно равна 4l). Эффекты нелинейности и дисперсии компенсируются, если эти добавки к скорости примерно равны, что и приводит к условию (7.2).
Если величина параметра S заметно больше единицы, то для достаточно плавного горбика высотой y0 и шириной 2l основную роль будут играть эффекты нелинейности. Он будет деформироваться и скорее всего распадется на несколько солитонов. Если S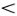 
1, то преобладает дисперсия, и горбик постепенно «расплывается». При S 
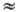1 горбик по форме близок к солитону. Если его скорость близка к скорости солитона, то он слегка деформируется и через некоторое время превратится в настоящий солитон, форма которого определяется формулой (7.1).
Для читателя, не вполне освоившегося с гиперболическими функциями, напомним, что ch х принимает наименьшее значение при х = 0, ch (0) = 1. При возрастании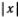 
функция ch х монотонно возрастает, так что ch2 (1) 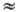2,4. Таким образом, вершина солитона расположена в точке х = vt, а величину 2l можно считать его «шириной», на которой в основном сосредоточена переносимая им энергия. Часть солитона, расположенную на большом расстоянии от центра, иногда называют «хвостом» солитона. Центральную часть естественно называть «головой». В «голове» сосредоточено почти 90 % жидкости, поднятой солитоном над поверхностью.
В ч. I мы привели выражение для скорости солитона Рассела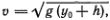 
, на первый взгляд не совпадающее с полученным для точного решения КдФ-уравнения. На самом деле величина скорости солитона v = 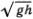[1 + (y0/2h)] не противоречит формуле Рассела. Нужно вспомнить только о сделанном предположении, что амплитуда y0 мала. Поэтому y0/h малая величина и
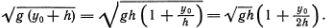
Вернемся теперь к численному эксперименту Забуски и Крускала с КдФ-уравнением. Приступая к нему, они уже были хорошо знакомы с солитонными решения (7.1) и с нелинейными периодическими волнами. Однако они довольно плохо представляли, как могут образовываться солитоны, и совершенно не знали, что произойдет, если солитоны столкнутся. Считалось, что солитоны либо распадутся при таком соударении, либо, в крайнем случае, могут образовать новый солитон, испустив некоторое количество нелинейных волн. Они поставили задачу примерно так же, как и Ферми, Паста и Улам. Задавали некоторое простое начальное возмущение поверхности воды у (0, х) и наблюдали, что с ним происходило с течением времени (на самом деле они изучали волны не в воде, а в плазме, но это совершенно несущественно, коль скоро использовалось одно и то же уравнение КдФ). Для того чтобы ЭВМ могла справиться с задачей, нужно, конечно, изучать этот процесс не на всей бесконечной оси Ох, а на некотором конечном участке О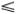 
х 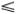L. Чтобы не думать о том, что происходит на границе, проще всего замкнуть этот отрезок, т. е. решать задачу на окружности.
Проследим за эволюцией простой гармонической волны у (0, х) = cos (2?х/L), рассчитанной ЭВМ. Начальная форма поверхности изображена на рис. 7.6 штрихпунктирой линией.
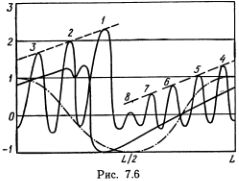
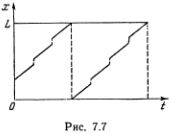
Через некоторое время Т эффекты нелинейности приводят к тому, что образуется характерная ступенька (штриховая линия). Спустя время 2,5 Т эта ступенька порождает последовательность солитонов (сплошная линия), которые перенумерованы в порядке убывания их амплитуд. Все они движутся направо, причем солитон, пересекающий правую границу, тут же появляется слева: вспомним, что они движутся по окружности, и точки х = 0, х = L соответствуют одной и той же точке этой окружности (как «концы» экватора на карте земного шара). Первый солитон движется быстрее всех остальных. Он догоняет их и последовательно сталкивается с ними. Примерный график движения его вершины изображен на рис. 7.7. Ступеньки соответствуют столкновениям с другими солитонами. Видно, что после столкновения он сохраняет скорость, но как бы ускоряется в самый момент столкновения. Это явление было объяснено в гл. 2 по аналогии со столкновениями упругих мячей.
Все эти результаты, полученные ЭВМ, удивили не только авторов работы, но и всех, кто с ними познакомился. Особенно большое впечатление произвел сделанный ЭВМ кинофильм, в котором можно было увидеть, как рождаются солитоны, как они сталкиваются друг с другом и что при этом с ними происходит.
Этот первый кинофильм из жизни солитонов был черно-белый и неозвученный. С тех пор было снято много таких фильмов, в том числе цветных и звуковых. Если бы удалось устроить фестиваль фильмов о солитонах, то на нем можно было бы, вероятно, узнать о солитонах больше, чем из нескольких книг, подобных этой. В недалеком будущем с развитием и удешевлением ЭВМ и видеозаписи изготовление видеофильмов во многих случаях заменит писание статей и книг. Но пока продолжим наше повествование в надежде, что заинтересованный читатель в конце концов сумеет посмотреть такие фильмы или даже сделать их самостоятельно...
На самом деле, наш рассказ подходит к естественному концу. После основополагающих работ 1965—1967 гг. усилиями многих физиков и математиков СССР, США, Японии и других стран была разработана математическая теория солитонов, составившая новый раздел математической физики. Невозможно рассказывать о дальнейшей истории солитонов, не касаясь идей и результатов этой теории. В то же время рассказать о ней, пользуясь тем скудным математическим языком, которым мы здесь ограничены, тоже невозможно.
Также обречена была бы на неудачу попытка описать все найденные за последние двадцать лет физические приложения идеи солитона. Трудно назвать область современной физики, в которой сегодня не изучались бы солитоны и солитоноподобные объекты. Поэтому простая экскурсия по «зоологическому саду» физических солитонов неизбежно превратится в долгое и нелегкое путешествие по всей современной физике.
Итак, «о том, что очень близко, мы лучше умолчим». Однако ставить точку пока рано! Нам еще нужно проследить за судьбой еще нескольких идей, зародившихся в прошлом веке, и описанных в гл. 3. Попутно, конечно, мы познакомимся с несколькими новыми применениями солитонов, однако это будет лишь беглое знакомство, не ждите от него многого. Оно будет похоже на быструю автомобильную экскурсию по Москве: «Справа мы видим здание Большого театра, построенное в 1824 г. по проекту Бове и Михайлова, слева — здание Малого театра и памятник Островскому работы Андреева, впереди — гостиница «Метрополь» с керамическим панно «Принцесса Греза» по рисунку Врубеля...». Примерно в таком стиле будет и наш рассказ...
Сначала, однако, завершим наш рассказ о численном эксперименте Ферми, Пасты и Улама. На самом деле Ферми, Пасте и Уламу просто «повезло». Если бы они смогли проследить за судьбой своей цепочки достаточно долго, они увидели бы, что возвращение к начальному состоянию постепенно становится все менее и менее точным и в конце концов устанавливается хаос.
Другое дело — описываемая КдФ-уравнением «струна» 3абуски и Крускала. В ней возвращение должно наблюдаться в принципе неограниченно долго. Оговорка «в принципе» связана с тем, что в реальном численном эксперименте происходит накопление ошибок и возвращение тоже перестает быть точным. Если бы вычисления производились абсолютно точно, то мы увидели бы, что солитоны, изображенные на рис. 7.6, много раз столкнувшись, в конце концов снова собрались бы в синусоидальную волну. После этого все началось бы сначала!
Физические системы, которые рано или поздно возвращаются в начальное состояние, называют интегрируемыми. К ним относятся все системы, в которых существуют настоящие солитоны. Простейший пример интегрируемой системы — маятник. Однако если есть трение, то свойство интегрируемости теряется и маятник не возвращается в начальное состояние. Если трение очень мало, то маятник с хорошим приближением можно считать интегрируемой системой и он возвращается в первоначальное состояние достаточно много раз. Точно так же цепочка Ферми — Пасты — Улама интегрируема лишь приближенно, даже если пренебречь трением и вычислительными ошибками. Существуют, однако, и точно интегрируемые цепочки атомов. В 1967 г. японский физик М. Тода показал, что если сила, действующая на атом со стороны его соседей, равна
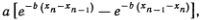
то цепочка будет интегрируемой и в ней существуют солитоны, совершенно подобные солитонам КдФ.
Но отправимся в нашу беглую экскурсию!