Фазовый портрет маятника

Как вообще в природе ни одно существо не походит

на другое, так и закон колебаний одного колеблюще-

гося тела не походит вполне на закон колебаний

другого...

Л. Больцман

Набросав все эскизы, попробуем теперь нарисовать портрет маятника. Чтобы облегчить эту задачу, изобразим сначала его движения на энергетической диаграмме (рис. 4.9). Вспомним, что связь между угловой скоростью ?' и углом отклонения ? определяется выражением для энергии (4.3), которое перепишем еще раз:

(?')²/?₀² + 4 sin² ?/2 = Е/E₀, E₀ = 1/2m?₀² l².

Если энергия равна нулю, то маятник покоится; график его движения — ось Ot, изображающая точка на энергетической диаграмме и на фазовой диаграмме — точка O.

Если Е/E₀ 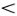 4, то существует максимальное значение угла отклонения ?_M  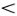?. Так как должно выполняться неравенство Е/E₀ - 4 sin² ?/2  0, то угол ? не может достигать значения ?. Мы знаем, что при этом маятник колеблется между значениями угла отклонения -?_M и +?_M. Движение это периодическое, хотя оно уже не описывается простой синусоидой и формула Гюйгенса не применима. (Вместо нее следует использовать более сложную формулу (4.2).) Графику этого движения (кривая 1 на рис. 4.9) соответствует на энергетической диаграмме движение по кривой 1 до крайней точки A₁, где кинетическая энергия и скорость равны нулю, а затем в обратном направлении до A'₁, где точка «отражается» и снова движется в положительном направлении. Как и в случае гармонического движения, на фазовой диаграмме изображающая точка движется по замкнутой кривой «овальной» формы. Ее легко построить с помощью уравнения (4.3), выразив ?' через ?. Если амплитуда ?_M мала, то этот «овал» превращается в окружность, соответствующую синусоиде на графике движения.

При достаточно большой энергии, когда Е/E₀ 4, и даже при максимальном значении потенциальной энергии 4 sin² (?/2) (при ? = ? потенциальная энергия равна 4) кинетическая энергия (?')²/?₀² не равна нулю, и маятник проскакивает верхнюю точку. Теперь он совершает не колебательное, а вращательное движение.

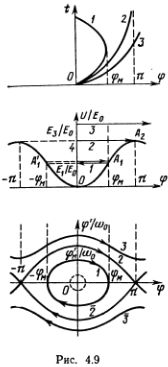
Это движение не равномерно, внизу скорость маятника максимальна, а в верхнем положении минимальна. На наших графиках это движение изображается кривыми 3. Если маятник вращается против часовой стрелки, значение угла ? неограниченно возрастает с ростом времени (фазовая траектория 3). Если он вращается по часовой стрелке, то значение угла неограниченно уменьшается (фазовая траектория 3).

Наиболее интересно для нас движение с энергией Е, в точности равной 4Е₀. В этом случае закон сохранения энергии дает простое соотношение

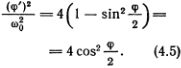
Если маятник находится в верхнем положении, т. е. ? = ? или ? = -?, то его скорость равна нулю, и он может пребывать в состоянии покоя. График такого движения: ?(t) = ? при всех t, или ?(t) = -? при всех t. На фазовой плоскости точки ? = ?, ?' = 0 и ? = -?, ?' = 0 — это точки покоя (или точки равновесия). Ясно, что эти точки равновесия, в отличие от нижней точки равновесия маятника, неустойчивы. Если чуть-чуть увеличить полную энергию, скажем, резким движением слегка толкнуть маятник, то он начнет совершать вращательное движение. Если уменьшить полную энергию, скажем, медленно сдвинуть и отпустить маятник, то он начнет совершать колебательные движения с амплитудой, близкой к ?. В обоих случаях он далеко уходит от положения равновесия. Если бы мы проделали то же самое в нижнем положении равновесия, то ясно, что маятник начал бы колебаться около этого положения с небольшой амплитудой. Точка ? = 0, ?' = 0 на фазовой плоскости — устойчивая точка покоя.

При Е = 4Е₀ возможно и другое движение маятника. Пусть при t = 0 угловая скорость ?' равна 2?₀. Тогда из формулы (4.3) следует, что Е/E₀ = 4, и маятник движется к верхней точке так, что его скорость в положении ? равна

 ?' = 2?₀cos ?/2 . (4.6) 

Чем ближе ? к ?, тем меньше скорость. Если угол отклонения очень близок к ?, то удобно обозначить малый угол отклонения ? - ? через 2?. Тогда cos (?/2) = cos (?/2 - ?) = sin ? 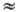 ?. Скорость изменения угла ? равна, очевидно, -2?'. Поэтому между ?' и ? при малом значении угла ? есть простое соотношение

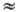?'  -?₀?, (4.7)

которое следует из (4.6) при малом значении ? - ?.

В уравнении (4.7) можно узнать уравнение, описывающее радиоактивный распад, если считать ?(t) массой нераспавшегося к моменту времени t радиоактивного вещества. Решение уравнения радиоактивного распада хорошо известно:

?(t) = ?₀е^-?₀t.

Здесь ?₀ — начальное количество вещества, ?(0) = ?₀, основание натуральных логарифмов е = 2,718281828... В Приложении показано, как получить это решение чисто геометрически. Здесь нам важно лишь то, что оно при возрастании t быстро убывает, но никогда не обращается в нуль. Это означает, что маятник ни за какое конечное время не придет в верхнее положение равновесия. Для понимания качественного характера движения нам больше ничего и не нужно. Можно сразу нарисовать приблизительный вид графика движения с энергией Е= 4Е₀. Правда, наши рассуждения относились лишь к положительным значениям времени t, но левую часть кривой легко построить, вспомнив, что маятник качается совершенно симметрично относительно нижнего положения (для сравнения тонкой кривой изображено колебательное движение с энергией, меньшей  4Е₀). Эта симметрия приводит к тому, что энергетическая и фазовая диаграммы симметричны относительно вертикальной оси. Если в какой-то момент t маятник находится в положении ?(t), то в момент -t он находился в положении ?(-t) = -?(t) (напомним, что время отсчитывается так, что в момент t = 0 маятник находится в нижнем положении, см. рис. 4.10).

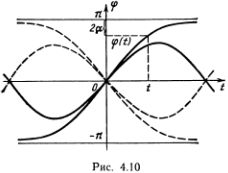
Фазовая диаграмма симметрична и относительно горизонтальной оси. Это значит, что всякому качанию слева направо, когда ? возрастает, соответствует точно такое же качание справа налево. График такого движения изображается кривой, симметричной относительно вертикальной оси (эти кривые изображены на рис. 4.10 штриховой линией).

Итак, мы нарисовали полный фазовый портрет маятника (рис. 4.9). Важную роль играют на нем кривые 2 и 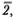которые отделяют фазовые траектории колебательных движений (кривая 1) от фазовых траекторий вращательных движений (кривые 3, 3) и называются сепаратрисами (от лат. seрaro — отделять). Эти кривые и соответствующие им графики движения играют, как мы скоро увидим, большую роль в теории солитонов. Форма солитона Френкеля и Конторовой (как и многих других солитонов) определяется кривой, совпадающей с графиком движения, соответствующим сепаратрисе.