Дислокации и маятники

В настоящей модели ФК атомы, естественно, движутся по прямой (ось х) и все силы, действующие на них, направлены также по оси х. Действие соседних атомов верхнего слоя представим, как всегда, пружинами, а действие атомов нижнего слоя («подкладки») описывается периодической синусоидальной силой

f(х) = -f₀ sin (2?x/?).

Как и в предыдущей главе, обозначим отклонение n-го атома от положения равновесия функцией y_n(t) = x_n(t) - n?, где x_n(t) — координата n-го атома. Со стороны «подкладки» на n-й атом действует сила

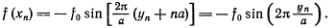
Пружины действуют на n-й атом с силой, равной

k (y_n+1 - y_n) - k (y_n - y_n-1).

Уравнение движения n-го атома поэтому принимает вид

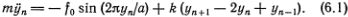
Если f₀ = 0, то мы получаем уравнение (5.8), уже изученное раньше.

Итак мы получили уравнение (6.1), соответствующее модели Френкеля — Конторовой. Сейчас мы найдем решение этого уравнения, описывающее движущуюся дислокацию. Читателя, разобравшегося в предыдущей главе, уже не смущает что это не одно уравнение, а бесконечная система уравнений. Мы знаем что движущаяся дислокация подобна волне, бегущей по цепочке маятников, в которой каждый маятник с некоторым запаздыванием точно повторяет все движения предыдущего. Время этого запаздывания ?t определяется скоростью перемещения волны v = ?/?t. Таким образом (вспомните рис. 5.7)

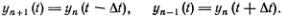
Смещения y_n (t + ?t) можно найти, считая движение атома от момента t - ?t до момента t + ?t равномерно ускоренным. Тогда, как мы уже писали,

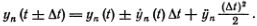
Подставляя это в уравнение (6.1), получаем замечательно простое уравнение

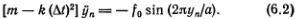
Присмотримся к этому уравнению повнимательнее. Если отвлечься от обозначений, то видно, что оно почти совпадает с уравнением маятника, о котором так много говорилось в гл. 4. Когда периодической силы не было, т. е. f₀ = 0, мы должны были положить m = k (?t)², откуда и определили скорость распространения звука в свободной цепочке:

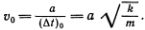
Теперь квадратная скобка не равна нулю. Перепишем ее в виде

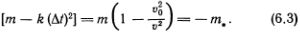
Теперь ясно, что при медленном движении дислокации, когда v 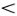v₀, квадратная скобка отрицательна, а определенная нами эффективная масса m_•, зависящая от скорости v, положительна.

Легко свести уравнение (6.2) к уравнению маятника (4.1). Вспомним, что sin (? + ?) = -sin ?, и положим 2?(y_n/?) = ? + ?_n, т. е. будем измерять отклонение атома от положения равновесия «углом» ?_n. Если атом остался на месте, то y_n = 0 и ?_n = -?. Если он смещается вправо, то угол ?_n возрастает и при y_n = ? принимает значение +?. Таким образом, переходу атома со дна одной «ямки» на дно другой соответствует асимптотическое движение «маятника». При таком изменении обозначений уравнение движения (6.2) можно записать в виде (проверьте это!)

Движение «маятника» по сепаратрисе, когда ?_n (t) изменяется от -? до +?, мы уже определили раньше (вспомним формулу (4.9) и рис. 4.10). Напишем эту формулу еще раз:

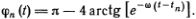
Так как маятники качаются с запаздыванием, мы выбрали свое начало отсчета времени t_n для каждого из маятников. Поскольку смещение атомов от ячейки к ячейке распространяется со скоростью v = ?/?t, надо взять t_n = n?t. Тогда ?₁(t) = ?₀(t - ?t), и вообще ?_n(t) = ?₀(t - n?t).

Выразим теперь t_n через скорость дислокации, т. е. t_n = n?•(?t/?) = n?/v, и заменим n? на х. Будем писать соответственно ?_n(t) = ?(t, х), где х = n?. Тогда функцию ?(t, х), описывающую движущуюся дислокацию, можно записать в виде

?(t, х) = ? - 4 arctg [e^{-?(t - x/v)}].

Эта функция определяет форму дислокации в любой момент времени:

y_n(t) = ?/2 + (?/2?) ? (t, n?).

Удобно записать показатель экспоненты в форме (х - vt)/l_v, где l_v = v/?. Вспоминая определения «частоты» ? и «массы» m_• (см. формулы (6.4) и (6.3)), после простых преобразований получаем

В этом выражении для величины l₀ под корнем написана безразмерная величина, равная отношению неких двух энергий. Выясним смысл этих энергий. Вспоминая, что v₀ = 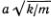, представим mv₀² как k?². Эта величина пропорциональна энергии, необходимой для растяжения пружины на величину порядка ?. В знаменателе стоит произведение силы f₀ на расстояние ?, что, очевидно, пропорционально работе, которую надо затратить на преодоление барьера, отделяющего одну ямку от другой. Таким образом, l₀ увеличивается при увеличении жесткости пружин и уменьшении силы со стороны «подкладки», привязывающей атомы к определенным местам. В дальнейшем будем считать, что упругая энергия k?² значительно превосходит f₀?, и, таким образом, величина l₀ ?.

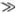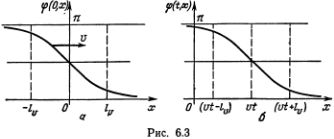
Теперь посмотрим на окончательное выражение для функции ?(t, х), описывающей дислокацию

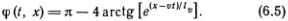
Эта функция представлена на рис. 6.3, б. На рис. 6.3, ? изображена кривая зависимости ? от х в момент t = 0. Вдали от центра дислокации, расположенного в точке х = 0, атомы расположены вблизи положений равновесия, т. е. ? 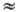? или ?  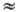-?. Атомы находятся далеко от положений равновесия лишь на расстояниях 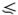l_v от центра. Мы можем поэтому называть l_v полушириной дислокации или просто ее размером:

Если скорость дислокации равна нулю, то ее размер l_v = l₀ зависит лишь от характеристик решетки. Размер равномерно движущейся дислокации t_v с увеличением скорости уменьшается, причем это уменьшение определяется формулой

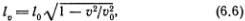
напоминающей преобразование длины при переходе в движущуюся систему координат в специальной теории относительности, только вместо скорости света с

в ней стоит скорость звука v₀. Эту аналогию с теорией относительности можно провести достаточно далеко. Можно показать, что энергия Е и импульс р движущейся дислокации также выражаются формулами «теории относительности»

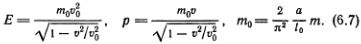
Таким образом, быстро движущиеся дислокации подчиняются не механике Ньютона, а механике специальной теории относительности. При малой скорости движения дислокации (v²/v₀² 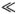  1) можно пользоваться обычной нерелятивистской теорией.

Эта модель, вероятно, очень понравилась бы Джозефу Лармору (1857—1942), считавшему частицы чем-то вроде дислокаций в эфире. Правда, его теория намного сложнее, но суть дела именно такая. С интересом отнесся бы к этой модели и Пуанкаре. В своем докладе «Новая механика» (1909 г.) он говорил: «Инерцией обладает не материя, а эфир; он один оказывает сопротивление движению, так что можно было бы сказать: нет материи, есть только дыры в эфире». В конце этой книги мы познакомимся с некоторыми современными идеями, связывающими элементарные частицы с солитонами некоторых нелинейных полей, играющих в какой-то степени роль эфира.