Океанические солитоны: цунами *), «девятый вал»
А волны в злобе постоянной бегут к прибрежью моему.
А. Фет
28 декабря 1908 г. на юге Италии произошло землетрясение, в результате которого погибло 82 тыс. человек. Страшные разрушения были вызваны также поднятой им гигантской волной, которая была описана М. Горьким: «...Поднялась к небу волна высоты неизмеримой, закрыла грудью половину неба и, качая белым хребтом, согнулась, переломилась, упала на берег и страшной тяжестью своею... смыла весь берег». Горький описал здесь цунами. Японское слово «цунами» обозначает просто «большую волну в гавани». Цунами чаще всего образуется, когда достаточно крупный, но безвредный в открытом океане солитон выбрасывается на берег. Не все цунами вызваны солитонами, но, по мнению специалистов, большинство цунами — солитонного происхождения.
*) Основные сведения о цунами заимствованы из книги: Пелиновский Е. Н. Нелинейная динамика волн цунами. — Горький: ИПФ АН СССР, 1982.
Чаще всего солитон в открытом океане образуется при землетрясении океанского дна. Длина его может достигать 500 км, но даже для относительно короткого солитона длиной 10 км океан можно считать мелким. Высота солитона в океане обычно невелика, не больше 10 м, и такую плавную волну трудно даже заметить. Среднюю скорость солитона вдали от берега легко вычислить по формуле v =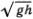 
. При h 
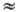1 км получаем v 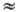100 м/с. При изменении рельефа дна эта скорость меняется в пределах от 50 до 700 км/ч. При подходе к берегу солитон замедляет движение, становится короче и выше.
Чтобы это увидеть, достаточно вспомнить соотношение (7.2) и учесть, что энергия солитона остается постоянной. Так как энергия солитона пропорциональна y02l, то условие ее постоянства удобно выразить, введя еще один параметр L с размерностью длины: L3 = y02l. Из (7.2) при S 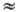1 из этого соотношения легко найти, что y0 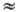L2/h, а l 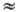h2/L. Для океанских солитонов значение L обычно равно нескольким десяткам метров. Эти простые соотношения, конечно, пригодны, пока L 
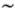h. При L 
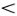h высота солитона y0 сравнивается с глубиной h, и нелинейность уже нельзя считать малой. Начинаются нелинейные процессы обрушивания волны, последняя стадия которых и описана Горьким.
Больше всех страдают от цунами, вызванных землетрясениями, Япония и Чили. Одно из самых сильных цунами обрушилось на Японию в 1896 г. Высота волны, обрушившейся на берег, достигла 30 м, погибло около 30 тыс. человек. Среди тех, кто читал о леденящих душу подробностях этого бедствия, наверняка были и немногочисленные читатели недавно полученного номера журнала со статьей Кортевега и де Фриза. Никому из них, однако, не пришла в голову мысль, что прочитанная ими сугубо математическая работа имеет самое прямое отношение к беде, постигшей жителей Японии. Солитонная теория цунами возникла лишь три четверти века спустя.
Самые важные проблемы, которые изучаются сегодня теорией цунами, это условия образования начальной волны и ее эволюция при подходе к берегу. Движение солитона в океане можно довольно неплохо рассчитать с помощью общей теории, но условия его рождения и его разрушительное действие очень сильно зависят от местных условий. Один и тот же солитон будет вести себя совершенно по-разному на открытом пологом берегу, в гавани или в устье реки (в последнем случае цунами часто порождает бор). Рождение солитона может быть вызвано разными причинами — землетрясением, взрывом вулкана или «искусственным» взрывом в воде, обвалом или оползнем берега. Например, взрыв вулкана Кракатау в 1883 г. привел к образованию на берегах Индонезии цунами с высотой до 45 м. Жертвами этой катастрофы стали 36 тыс. человек. Специалисты считают, что энергия этого взрыва была равна энергии взрыва сотен тысяч атомных бомб, подобных сброшенной на Хиросиму. Между прочим, существует гипотеза, что цунами, вызванное взрывом вулкана в Эгейском море, погубило 3,5 тыс. лет назад легендарную Атлантиду.
Ясно, что для предсказания цунами и оценки их разрушительной силы нужно выполнить еще много экспериментов на лабораторных моделях и расчетов на ЭВМ математических моделей цунами. Этим занимаются многие коллективы ученых, особенно в странах, которым угрожает это бедствие (в нашей стране цунами иногда «посещает» Камчатку и Курильские острова). В недалеком будущем, когда расчеты цунами смогут делать самые мощные и самые быстродействующие ЭВМ («суперкомпьютеры»), бедственные последствия набегов солитонов можно будет свести к минимуму.
Между прочим, известны случаи, когда «микроцунами» возникали от движения корабля. В начале века, когда стали появляться быстроходные военные суда, их капитаны время от времени сталкивались со «спутной волной», которая образуется при движении судна со скоростью, близкой к 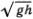. Оторвавшаяся от судна спутная волна и солитон Рассела это одно и то же. Отличие лишь в том, что в мелком канале спутная волна возникает при небольшой скорости движения *). Если судно, образовавшее спутную волну, внезапно замедлит ход или если глубина внезапно изменится, спутная волна оторвется от судна и, отправившись в самостоятельное путешествие, может наделать бед. Один такой несчастный случай, произошедший в 1912 г. в Финском заливе, расследовал академик А. Н. Крылов. Он подробно описал его в своих интереснейших воспоминаниях. К сожалению, Крылов не знал о работах Рассела и Кортевега и де Фриза; подробно изучив это явление, он ограничился лишь выработкой практических рекомендаций для капитанов.
*) Рассел приписывает первое наблюдение отрыва баржи от спутной волны при увеличении скорости и вызванное этим уменьшение сопротивления движению баржи «Уильяму Хаустону, эсквайру», который, однако, осознал лишь «коммерческое значение этого факта для компании канала, с которой он был связан». Научное значение этого явления первым понял Рассел.
В океане рождаются и путешествуют самые разные солитоны. Безгранично разнообразный и сложный океан — естественная «среда обитания» для них. Некоторые океанские солитоны неплохо изучены, о существовании иных мы, может быть, пока и не подозреваем. Волны и солитоны могут возникать не только на поверхности воды, но и в глубине. Океанские глубины очень неоднородны, в них существуют слои воды с разной температурой, плотностью, соленостью. Зачастую граница между этими слоями оказывается довольно резкой. Она, как говорят, образует поверхность раздела. По такой поверхности, как и по поверхности раздела воды и воздуха, тоже путешествуют волны и солитоны, которые могут оказаться довольно опасными. Не исключено, что подобные солитоны ответственны за случаи загадочных аварий подводных лодок.
Ты волна моя морская,
Своенравная волна,
Как, покоясь иль играя,
Чудной жизни ты полна.
Ф. Тютчев
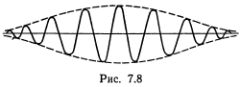
Перейдем теперь к солитону, который был на глазах у людей с незапамятных времен, но в науку проник совсем недавно. Речь идет о группах («стаях») волн, вызванных ветром на глубокой воде (рис. 7.8).
Нельзя сказать, что ученые совсем не пытались выяснить, почему волны собираются в такие стаи, но к реальному ответу на этот вопрос удалось приблизиться лишь после того, как в 1967 г. Т. Бенжамен и Дж. Фейр показали теоретическими расчетами и опытами, что простая периодическая волна на глубокой воде неустойчива. Иными словами, она склонна разбиваться на группы волн. Уравнения, описывающие такие группы, в следующем году нашел В. Е. Захаров, а вскоре было доказано, что они обладают всеми свойствами настоящих солитонов. Эти солитоны составляют новую разновидность, с которой мы еще не встречались. Они внешне похожи на модулированные радиоволны или оптические импульсы. Однако электромагнитные группы волн могут распространяться в пустоте без искажений, а группы волн на глубокой воде очень быстро расплылись бы из-за сильной дисперсии (v =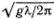 
), если бы этому не препятствовала нелинейность.
И эти солитоны имеют непростую историю. Физики сталкивались с такими солитонами в нелинейной оптике, а уравнения, описывающие их, еще раньше изучались в теориях сверхтекучести и сверхпроводимости.
Солитон, изображенный на рис. 7.8, обычно называют «солитоном огибающей», мы будем также называть его «групповым» солитоном. Название это напоминает о том, что привычную солитонную форму имеет штриховая линия, огибающая верхушки волн. Сами эти волны движутся с иной скоростью, чем их огибающая, так что под ней идет бурная жизнь. Волны, на которых «сидит» солитон, приблизительно монохроматичны. Форма огибающей описывается выражением
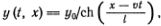
причем размер солитона 2l определяется его амплитудой y0, а скорость v от амплитуды не зависит. Этим «групповые» солитоны существенно отличаются от солитонов Рассела — КдФ, а в остальном они весьма сходны. Обычно под огибающей может спрятаться не более 14—20 волн, причем средняя — самая высокая. Это и объясняет давно известное морякам правило, что самая высокая волна в группе седьмая — десятая (отсюда и «девятый вал»). Солитоны c большим числом гребней несущей волны неустойчивы и распадаются на меньшие.
На этом мы и закончим знакомство с океанскими волнами и солитонами. То, что было рассказано, разумеется, лишь карикатура, но эта карикатура позволила нам разглядеть очень важные и простые явления. Волны в реальном океане гораздо более сложны, многообразны и хаотичны *).
*) О реальных морских волнах можно прочесть в популярной книге: Кадомцев Б. Е., Рыдник В. И. Волны вокруг нас. — М.: Знание, 1981.
Передо мною волны моря.
Их много. Им немыслим счет.
Волна подаст свой голос в хоре
И новой очереди ждет.
Б. Пастернак
Нам хотелось бы рассказать еще о нескольких солитонах, но сначала подведем предварительные итоги, вспомним самые главные свойства истинных солитонов.