Заключительные замечания
Метод необходим для отыскания истины.
Р. Декарт
Мы заканчиваем самую трудную главу в этой книге, главное содержание которой — основные идеи теории нелинейных колебаний, изложенные на простейших, но не тривиальных примерах. Читателю, желающему понять, как устроены солитоны, необходимо ясно представить себе линейные и нелинейные колебания маятника. Особенно хорошо нужно понять энергетические соотношения и движения, фазовые траектории которых сепаратрисы (формулы (4.9), (4.10) и рис. 4.14). Эти решения позволят нам понять с помощью простых аналогий очень важные солитоны. Один из примеров — ручной солитон, который связан с асимптотическим движением маятника аналогией Кирхгофа.
И я больше всего дорожу аналогиями,
моими самыми верными учителями.
И. Кеплер
Метод физических аналогий и моделей, которым с таким успехом пользовались великие физики прошлого века, и сегодня сохраняет ценность. Особенно плодотворен он в теории колебаний, волн и солитонов, где одни и те же уравнения описывают множество совершенно различных систем. Можно высказать некоторые общие принципы получения таких аналогий. Пусть состояния двух систем определяются одинаковым числом переменных, или, как говорят, обобщенных координат (например, угол ? для маятника, заряд конденсатора Q в колебательном контуре и т. д.). Предположим, что энергии этих систем Е1 и Е2 сохраняются и что посредством некоторого переобозначения обобщенных координат и параметров, характеризующих системы (массы, емкости, индуктивности и т. д.), можно сделать величины Е1 и Е2 одинаковыми функциями координат (с точностью до постоянного множителя). Тогда ясно, что системы полностью аналогичны и между их «движениями», каков бы ни был их смысл, можно установить полное соответствие.
Правда, здесь есть некоторые тонкости. Например, новые обобщенные координаты, от которых энергии зависят одинаково, могут изменяться в разных пределах. Более существенная тонкость связана с тем, что для систем разной природы нас могут интересовать разные задачи. Если между системами имеется точная аналогия, то их обобщенные координаты удовлетворяют одинаковым уравнениям движения. (Собственно, это и есть определение точной аналогии, просто иногда удобнее иметь дело с энергией.) Однако мы знаем, что для определения конкретного движения нужно задать некоторые дополнительные условия, например, начальные значения координат и скоростей.
Рассмотрим с этой точки зрения аналогию Кирхгофа. Выше упоминалось о точном соответствии между движением маятника и формой изгиба упругой проволочки (эластика Эйлера). В следующей главе будет показано, что для определения эластики Эйлера нужно решить уравнение маятника ?" = -?02 sin ?. Однако в этом случае задача ставится совсем не так, как в теории маятника. Аналог времени здесь — длина дуги эластики s, а длина проволочки l фиксирована, так что -1/2l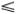 
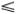s 1/2l. Нам нужно найти форму проволочки, т. е. ?(s) при заданной внешней силе F. Как мы увидим ниже, величина ?02 пропорциональна F. Если пользоваться аналогией с маятником, то нужно решить довольно странную задачу: найти все возможные движения маятника от «момента» -1/2l до «момента» +1/2l и изучить зависимость этих движений от ?02. Для эластики естественно возникают и другие задачи, например, как найти ее наиболее устойчивую форму, т. е. форму, для которой запасенная в проволочке упругая энергия минимальна. Эти задачи существенно сложнее задач, обычно решаемых в теории маятника, и знакомство с аналогичными, но более просто определяемыми движениями маятника очень помогает при их решении.
Полезны не только точные, но и приближенные аналогии. Типичный пример приближенной аналогии — соотношение между обычным и циклоидальным маятником. Приближенной аналогией следует пользоваться с большей осторожностью, чем точной. Например, при достаточно больших амплитудах колебания обычного и циклоидального маятника становятся качественно различными. Более удачна качественная аналогия между маятником и грузиком на кривой у = ? [1 - cos (х/Ь)] в поле силы тяжести, направленной по оси у (грузик в желобе). Введя обозначение ? = х/Ь, можно проверить, что малые колебания грузика вблизи точки ? = 0 соответствуют малым колебаниям маятника с длиной l = b2/? и что для этих двух систем фазовые портреты качественно сходны. На математическом языке можно сказать, что они топологически эквивалентны *). Простой пример такой эквивалентности — изображение нашего лица в кривом зеркале «комнаты смеха».
*) Топологически эквивалентные фазовые портреты легко получить, нарисовав какой-нибудь фазовый портрет на резиновой пленке. Любой портрет, который получается растягиванием пленки без разрывов, топологически эквивалентен исходному. При этом замкнутые кривые остаются замкнутыми, непересекающиеся кривые остаются непересекающимися и т. д.
Топологическую эквивалентность фазовых портретов можно было бы положить в основу определения качественной эквивалентности. Однако с этим связана еще одна тонкость. Все изучаемые в физике модели реальных систем описывают их реальное поведение лишь с какой-то степенью точности. Любая математическая модель физического явления получается упрощением, или идеализацией, реальной системы. Чем сложнее система, тем серьезнее эти упрощения.
Как говорил Я. И. Френкель, «физик-теоретик... подобен художнику-карикатуристу, который должен воспроизвести оригинал не во всех деталях, подобно фотографическому аппарату, но упростить и схематизировать его таким образом, чтобы выявить и подчеркнуть наиболее характерные черты. Фотографической точности можно — и следует — требовать лишь от теоретического описания простейших систем. Хорошая теория сложных систем должна представлять лишь хорошую «карикатуру» на эти системы, утрирующую те свойства их, которые являются наиболее типическими, и умышленно игнорирующую все остальные — несущественные свойства... Хорошая карикатура на какого-либо человека не может существенно улучшиться от более аккуратного и точного изображения нехарактерных деталей его лица и фигуры» *). Так вот, основная тонкость состоит как раз в том, чтобы выделить эти наиболее характерные черты.
*) Чтобы вполне оценить это высказывание, надо знать, что Я. И. Френкель с детства и до конца жизни помимо физики увлекался живописью. Выполненные им портреты друзей и знакомых обычно передают наиболее существенные черты оригинала, хотя и не являются карикатурами. Может быть, лучше вспомнить не о карикатурах, а о рисунках Пушкина или Пикассо, которые несколькими штрихами удивительно точно передают внутреннюю сущность изображаемого человека.
Когда мы хорошо понимаем вопрос, нужно освободить
его от всех излишних представлений, свести его к про-
стейшим элементам.
Р. Декарт
Без отбрасывания несущественных подробностей вообще нельзя было бы найти физические законы. Первым это понял Галилей, который и считается основателем современного научного метода в физике. Яркий пример силы метода «окарикатуривания» явления — открытие Галилеем закона инерции, который обычно называют первым законом Ньютона (сам Ньютон приписывал первые два «закона Ньютона» Галилею). Первая часть закона инерции Галилея была известна уже великому философу древности Аристотелю из Стагира (384—322 гг. до н. э.): «ни одно тело не переходит из состояния покоя в состояние движения без действия какой-либо силы». Представить себе, что равномерное и прямолинейное движение может происходить без действия какой-либо силы (в этом смысле состояние покоя эквивалентно состоянию равномерного прямолинейного движения), ни Аристотель, ни его последователи не могли. Увидеть это на опыте нельзя, как невозможно и доказать логическими рассуждениями. Поэтому открытие Галилеем закона инерции и связанного с ним принципа относительности — одно из величайших достижений человеческого интеллекта и воображения, а работу, которая привела к этому открытию, справедливо сравнить не с работой карикатуриста, но с творческим порывом поэта: «сотри случайные черты — и ты увидишь: мир прекрасен» (А. Блок).
Приближенное представление об идеальном движении дает скольжение конькобежца по льду (автору, правда, неизвестно, знал ли Галилей, что такое коньки). Можно представить себе, что действие силы тяжести уравновешивается реакцией со стороны льда (видимо, у Галилея было об этом некоторое представление). Чтобы получить теперь картину идеального состояния равномерного и прямолинейного движения, необходимо еще мысленно исключить силы трения. Галилей сумел сделать этот последний шаг, хотя он и не изучал силы трения на опыте.
Ясное понятие о сопротивлении среды, о силах трения впервые появилось в «Началах» Ньютона, который наблюдал качания маятника в сопротивляющейся среде. Он рассмотрел влияние силы трения, пропорциональной скорости тела, квадрату скорости тела, а также постоянную силу трения. В шестом разделе второй книги «Начал» Ньютон доказывает несколько теорем о качаниях маятника в сопротивляющейся среде. Замечательна своей простотой и очень важна теорема 21: «Качания маятников по циклоиде в среде, оказывающей сопротивление, пропорциональное скорости, изохронны» (попробуйте доказать эту теорему).
С помощью полученных теорем Ньютон попытался на опыте определить зависимость силы сопротивления от скорости: «Я подвесил к прочному крюку на тонкой нити деревянный шар, вес коего был 57 7/22 римский унций *) и диаметр 6 7/8 английских дюйма, так что расстояние между крюком и центром качания шара было 10? фута: на нити я отметил точку на расстоянии в 10 футов 1 дюйм от центра подвеса, и против этой точки я установил линейку, разделенную на дюймы, по которой я и замечал длины дуг, описываемых маятником. Затем я сосчитал число размахов, после которого маятник утрачивал восьмую часть величины своего размаха...». Сравнивая результаты наблюдений с доказанными теоремами, Ньютон пришел к выводу, что «сопротивление шара, когда он движется быстрее, пропорционально квадрату скорости, когда же медленнее, то немного более, нежели первой ее степени».
*) Римская унция равна примерно 31,1 г.
Опыты Ньютона были повторены в 1915 г. по предложению А. Н. Крылова, в переводе которого мы цитировали «Начала». Хотя методика Ньютона была заметно улучшена, его качественные результаты подтвердились. Однако, пользуясь столь несовершенными методами, трудно было установить количественные законы трения при движении тел в жидкостях и газах. Основные законы трения качения и скольжения твердых тел были установлены на опыте почти через сто лет после выхода в свет «Начал» работами Шарля Огюстена Кулона (1736—1806), наиболее известного открытием закона притяжения электрических зарядов, сделанного независимо от Кавендиша, по обыкновению, не опубликовавшего свои результаты. Чем все это интересно и важно? Наиболее важно, что идеализация явления привела к установлению общих законов. После того как законы установлены, можно выделить и понять «внешние силы», которые приводят к видимому нарушению этих законов. В результате — совершенно новый уровень понимания явлений: «Познай, где свет, — поймешь, где тьма!» (А. Блок).
Интересен также ход мыслей Ньютона. Изложение его, конечно, несовременно, и за деталями рассуждений следить трудно, но общий подход к проблеме не отличается от подхода современного физика. В современных курсах теоретической физики трение вводят, руководствуясь практически такими же соображениями, какими пользовался Ньютон, только обычно ограничиваются трением, пропорциональным скорости, чтобы не слишком сильно «испортить» общие законы. Силы трения здесь действительно выглядят «случайными чертами», которые нужно «стереть». Галилей и Ньютон оставили нам образцы такой работы мысли, выявляющей скрытую красоту законов природы.
Следуя их примеру, мы без стеснения отбросили силы трения при анализе нелинейных колебаний. Оправдано ли это? Может показаться, что нарисованный нами портрет маятника — лишь скверная карикатура реального маятника.
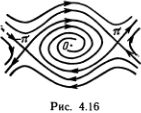
Действительно, что произойдет с портретом на рис. 4.9, если включить даже очень малую силу трения? Замкнутые линии 1, соответствующие колебательному движению, разорвутся и превратятся в спирали, накручивающиеся на точку O. Сепаратриса 2 оторвется от точки (?, 0) и тоже начнет накручиваться на O. Сепаратриса 
оторвется от точки (-?, 0) и т. д. (рис. 4.16). Короче, портрет маятника с трением топологически не эквивалентен портрету маятника без трения. Так что же? Выходит, трение нельзя признать случайной и нехарактерной чертой движений маятника? Не будем спешить с ответом.
Поразмыслив еще немного, можно увидеть, что рисование портрета «идеального» маятника все же не было пустым занятием. Во-первых, при малом трении фазовые траектории реального маятника достаточно близки к идеальным. Во-вторых, и это самое главное, при описании солитонов нам встретится уравнение маятника без всяких добавок, подобных силам трения. Иными словами, для теории солитонов важна аналогия не с реальным, а с идеальным маятником. Как мы скоро увидим, солитон Френкеля — Конторовой, как ручной солитон и многие другие, описывается асимптотическими движениями маятника, фазовые траектории которых — сепаратрисы 2 и . Поэтому с точки зрения теории солитонов трение в реальном маятнике, действительно, нехарактерно и случайно, а портрет идеального маятника — очень удачная карикатура. Добавление «нехарактерной детали» — трения — не только не улучшает ее, но катастрофически портит, уничтожая самое важное.
Наконец, последнее замечание. Для описания движений маятников было использовано некоторое количество математики. Необходимо ли это? Если бы нас интересовали лишь движения реальных маятников, можно было бы обойтись законом сохранения энергии, простыми геометрическими соображениями и здравым смыслом, почерпнутым из простых наблюдений. Для понимания наиболее интересных асимптотических движений этого, однако, мало, и знание математического языка хотя бы в объеме этой главы реально необходимо. О мере, в какой оно необходимо, хорошо сказал Л. И. Мандельштам в «Лекциях по колебаниям». Изложив «без всякой математики» простую картину описания колебаний грузика в желобе на языке сохранения энергии, он продолжает: «В такой простой картине все следует из наглядности. Зачем же мы проделали в прошлый раз ряд математических выводов? Дело в том, что «житейские» разговоры, в сущности, грешат в одном месте. Пусть кинетическая энергия грузика меньше максимальной потенциальной. Мы знаем, что в таком случае грузик должен остановиться. Но уверены ли мы, что он дойдет до точки остановки за конечное время? Ведь только при этом условии можно говорить о периодическом движении с конечным периодом. А что будет в случае лимитационного движения *)? Может быть, и в этом случае частица доходит до крайнего положения за конечное время? Здесь наглядные рассуждения ничего не дают, а необходимо математическое исследование. Без него вы не получите серьезного ответа. Начинающему часто кажется: к чему вся эта математика? Ему кажется, что «и так все ясно». Но в действительности какой-нибудь пункт при этом может остаться неясным. Иметь меру требуемой математической строгости — самое трудное для физика. Правильнее будет сказать так: ему необходимо уметь определять эту меру». Будем надеяться, что нам это удалось, и попробуем в том же духе подойти к изучению волн.
*) Это то же самое, что движение по сепаратрисе (см. (4.9)).