Сохранение энергии

Попался на качели,

Качайся, черт с тобой!

Ф. Сологуб

Кинетическая энергия грузика, подвешенного на нити и совершающего малые колебания, равна 1/2mv² = 1/2ml²(?')², а потенциальную энергию легко найти с помощью рис. 4.5.

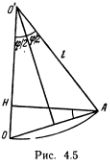
Так как (ОА) = 2l sin(?/2), то (ОН) = 2l sin²(?/2), и потенциальная энергия равна 2mgl sin² (?/2). Полная энергия Е = 1/2ml²(?') + 2mgl sin²(?/2).

Удобно намного преобразовать это соотношение, сделав все его члены безразмерными:

(?')²/?₀² + 4 sin² (?/2) = 2Е/m?₀² l² . (4.3)

В правой части здесь написано отношение полной энергии маятника к кинетической энергии точки с массой m, равномерно вращающейся по окружности радиуса l с периодом 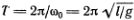. Обозначим эту энергию буквой Е₀, так что правая часть равна отношению Е/Е₀. Если амплитуда качаний ?_M мала, то sin(?/2)  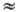?/2, и закон сохранения энергии (4.3) имеет совсем простой вид

(?')²/?₀² + ?² 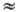Е/Е₀, Е₀ = 1/2m?₀² l². (4.4)

Полную энергию удобно выразить через амплитуду ?_M. В крайней точке, где ? = ?_M, угловая скорость равна нулю. Из уравнения (4.3) поэтому следует, что

Е/Е₀ = 4 sin²(?_M/2) 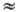?_M²,

где приближенное равенство, как всегда, относится к малым колебаниям.

С законом сохранения энергии связаны два новых способа наглядного графического изображения движений и других механических систем. Обычный способ — это изображение зависимости ?(t). Например, график простого гармонического колебания ? = ?_Msin(?₀t) позволяет наглядно представить положение грузика в разные моменты времени (рис. 4.6).

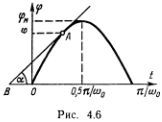
С помощью этого графика можно также найти скорость грузика в любой заданный момент. Она определяется углом наклона касательной BА к кривой в точке А с координатами (t, ?(t)), т. е. ?' = tg ?. На графике, однако, не видно, как распределяется полная энергия при движении и как она связана с амплитудой. Для наглядного представления изменения кинетической и потенциальной энергий грузика нарисуем энергетическую диаграмму.

Нарисуем зависимость потенциальной энергии грузика U(?) от его положения. В формуле (4.4) потенциальную энергию представляет слагаемое ?², а кинетическую Т — слагаемое (?')²/?₀². На графике удобнее откладывать отношения U/Е₀, Т/Е₀, Е/Е₀.

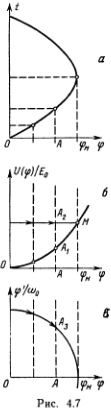
Отложим по горизонтальной оси отрезок ОА, длина которого равна ?(t), а в направлении вертикальной оси отложим отрезок (АА₂) = Е/Е₀, причем (АА₁) = U/Е₀, (А₁А₂) = Т/Е₀ (рис. 4.7, б). Так как полная энергия постоянна, то точка А₂ при изменении t будет двигаться по прямолинейному отрезку А₂М, а точка А' — по параболе (U(?)/Е₀) = ?². На энергетической диаграмме видно, как перераспределяется полная энергия между кинетической и потенциальной составляющими при различных значениях ? и как амплитуда связана с полной энергией. Если нарисовать над энергетической диаграммой график ?(t) (рис. 4.7, ?), то можно наглядно увидеть зависимость кинетической и потенциальной энергии от времени. Когда маятник движется из нижнего положения к крайнему правому, где ? = ?_M, изображающая точка А₂ движется направо до точки М, а затем возвращается налево. Как при этом меняются кинетическая и потенциальная энергия, видно достаточно ясно, но скорость определять не очень удобно (нужно вычислять квадратный корень из длины отрезка А₁А₂). Чтобы следить также и за положением и скоростью грузика, удобно представить движение еще одним способом.

Нарисуем под нашими двумя диаграммами еще одну, на которой по оси абсцисс по-прежнему будем откладывать значения ?, а по оси ординат отложим значения ?'/?₀ в тот же момент времени (рис. 4.7, в). Тогда при движении грузика точка А₃ будет описывать окружность с радиусом, равным ?_M = 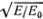. Это видно из уравнения (4.4), так как (ОА) = ?(t) и (АА₃) = ?'(t)/?₀. В случае простого гармонического колебания (ОА) = ?_Msin(?₀t), (АА₃) = ?_Mcos(?₀t), и ясно, что точка А₃ вращается по окружности равномерно.

В этом месте внимательный, но нетерпеливый читатель воскликнет: «Но ведь это же очевидно! С этого начиналось описание гармонического колебания. Более того, мы вернулись просто к определению тригонометрических функций. Всем известно, что если точка равномерно движется по окружности единичного радиуса с угловой скоростью ?₀, то ее проекции на прямые, проходящие через центр, определяют тригонометрические функции. В данном случае сразу ясно, что (ОА) = ?_Msin(?₀t)».

Все это, конечно, верно. Но дело в том, что нарисовать зависимость скорости ?' от положения ? можно, не только не решая уравнения маятника, но даже и забыв о его существовании. Достаточно знать закон сохранения энергии и выражение для энергии через координату и скорость, а это можно сделать не только для малых качаний маятника и не только для маятника! Пользуясь диаграммой зависимости скорости от положения, можно, наоборот, приближенно найти, как меняется положение точки со временем.

Диаграмму, на которой изображена зависимость скорости от координаты при различных значениях энергии, называют фазовой диаграммой. «Фаза» здесь означает состояние частицы, определяемое ее координатой и скоростью.

По фазовой диаграмме можно приближенно найти и график движения. Читателю полезно обдумать, как это сделать.