Начало теории волн

Хотя основные уравнения, описывающие движения жидкости, в 30-е годы ХIХ в. были уже получены, математическая теория волн на воде только начала создаваться. Простейшая теория волн на поверхности воды была дана Ньютоном в его «Математических началах натуральной философии», впервые изданных в 1687 г. Сто лет спустя знаменитый французский математик Жозеф Луи Лагранж (1736—1813) назвал этот труд «величайшим произведением человеческого ума». К сожалению, эта теория была основана на неправильном допущении, что частицы воды в волне просто колеблются вверх вниз. Несмотря на то, что Ньютон не дал правильного описания волн на воде, он верно поставил задачу, и его простая модель вызвала к жизни другие исследования. Впервые правильный подход к поверхностным волнам был найден Лагранжем. Он понял, как можно построить теорию волн на воде в двух простых случаях — для волн с малой амплитудой («мелкие волны») и для волн в сосудах, глубина которых мала по сравнению с длиной волны («мелкая вода»). Лагранж не занимался детальной разработкой теории волн, так как его увлекали другие, более общие математические проблемы.

Много ли есть людей, которые, любуясь игрой волн

на поверхности ручейка, думают, как найти уравнения,

по которым можно было бы вычислить форму любого волнового

гребня?

Л. Больцман

Вскоре было найдено точное и удивительно простое решение уравнений, описывающих волны на воде. Это первое, и одно из немногих точных, решение уравнений гидромеханики получил в 1802 г. чешский ученый, профессор математики в Праге Франтишек Йозеф Герстнер (1756—1832)*).

_{*) Иногда Ф. Й. Герстнера путают с его сыном, Ф. А. Герстнером, несколько лет жившим в России. Под его руководством в 18З6—18З7 гг. была построена первая в России железная дорога (из Петербурга в Царское Село).}

В волне Герстнера (рис. 1.1), которая может образоваться только на «глубокой воде», когда длина волны много меньше глубины сосуда, частицы жидкости движутся по окружностям.

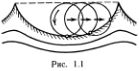
Волна Герстнера — первая изученная волна несинусоидальной формы. Из того, что частицы жидкости движутся по окружностям, можно заключить, что поверхность воды имеет форму циклоиды (от греч. «киклос» — круг и «эйдос» — форма), т. е. кривой, которую описывает какая-нибудь точка колеса, катящегося по ровной дороге. Иногда эту кривую называют трохоидой (от греч. «трохос» — колесо), а волны Герстнера трохоидальными *). Только для очень мелких волн, когда высота волн становится много меньше их длины, циклоида становится похожей на синусоиду, и волна Герстнера превращается в синусоидальную. Хотя при этом частицы воды и мало отклоняются от своих положений равновесия, движутся они все равно по окружностям, а не качаются вверх-вниз, как полагал Ньютон. Надо заметить, что Ньютон ясно сознавал ошибочность такого допущения, но счел возможным воспользоваться им для грубой приближенной оценки скорости распространения волны: «Все происходит таким образом при предположении, что частицы воды поднимаются и опускаются по отвесным прямым линиям, но их движение вверх и вниз на самом деле происходит не по прямой, а вернее по кругу, поэтому я утверждаю, что время дается этим положениям лишь приближенно». Здесь «время» — период колебаний Т в каждой точке; скорость волны ? = ?/Т, где ? — длина волны. Ньютон показал, что скорость волны на воде пропорциональна 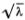. В дальнейшем мы увидим, что это правильный результат, и найдем коэффициент пропорциональности, который был известен Ньютону лишь приближенно.

_{*) Мы будем называть циклоидами кривые, описываемые точками, лежащими на ободе колеса, а трохоидами кривые, описываемые точками между ободом и осью.}