Волны в цепочке связанных частиц
Рассмотрим цепочку одинаковых частиц с массой m, соединенных упругими пружинками и движущихся по прямой. Физики называют эту систему моделью одномерного кристалла. Условимся поэтому называть частицы «атомами». Кавычки напоминают о том, что эти «атомы» пока не имеют никакого отношения к реальным физическим атомам. В дальнейшем мы их опускаем.
Пусть длина каждой пружинки в недеформированном состоянии равна ?. Тогда покоящиеся атомы, перенумерованные, как указано на рис. 5.1, будут располагаться в точках с координатами n?, т. е. равновесное положение n-гo атома определяется координатой x0n = n?. Допустим теперь, что атомы отклонены от равновесного положения, так что координата n-гo атома равна хn (верхнее положение). Обозначим отклонение атома от равновесного положения буквой yn = хn - х0n = хn - n? и отложим отрезки yn над соответствующими точками x0n = n?.
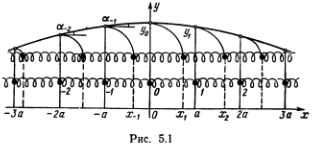
Соединив их плавной кривой, получим график, изображающий отклонения атомов от положений равновесия.
Плавная кривая получится, конечно, не всегда. Если отклонения каких-нибудь соседних атомов отличаются достаточно сильно, то у кривой будут резкие изломы. Мы поэтому предположим, что наклон графика отклонений очень медленно меняется, Т. е. разность двух последовательных углов ?n по модулю много меньше самих углов.
При этом получится плавная кривая, мало изменяющаяся на расстоянии ?, и наша модель будет достаточно точно воспроизводить смещения частицы в непрерывной (сплошной) среде. Другими словами, если мы хотим на модели воспроизвести распространение волны в сплошной среде (упругая волна в стержне, звуковая волна в органной трубе, волна на скрипичной струне и т. д.), нужно брать частички малыми и располагать их на малых расстояниях друг от друга. Сверх этого, длина волны ? должна быть много больше расстояния между атомами.
Картину распространения волн в такой цепочке можно изучить на очень простом устройстве, для изготовления которого нужна хорошая и достаточно длинная плоская резиновая лента и большие скрепки (см. рис. 5.2). Разумеется, эта система гораздо сложнее, чем идеальная одномерная цепочка, и к тому же очень несовершенна.
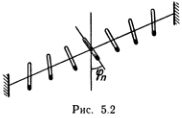
Главный ее недостаток — большие потери на трение в резине. Достоинство ее — небольшая скорость распространения волн. Это позволяет наблюдать бегущие по цепочке волны невооруженным глазом. Скорость распространения возбуждений можно изменять, утяжеляя скрепки. Интуитивно ясно, что с увеличением массы скрепок эта скорость должна уменьшаться.
Если скрепки закреплены на ленте в их центрах тяжести, так что сила тяжести не создает дополнительного вращательного момента, действующего на скрепки, то эта система вполне аналогична линейной цепочке. При этом угол ?n аналогичен отклонению yn, а роль массы грузика играет момент инерции скрепки.
Вместо возвращающей упругой силы нужно рассматривать момент упругой силы, возникающий при скручивании резинки. Короче, аналогия здесь такая же, как аналогия колебаний грузика на пружинке и крутильных колебаний.
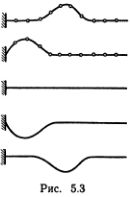
Еще одно существенное отличие нашей грубой модели от идеальной бесконечной цепочки связано с отражением волн от границ. Это происходит примерно так, как указано на рис. 5.3, где изображены графики отклонений грузиков или скрепок в последовательные моменты времени. Горбику соответствует смещение грузиков в положительном направлении оси х, впадине — в отрицательном. Когда горбик подходит к стенке, крайняя, закрепленная пружина начинает тянуть крайний грузик влево, он тянет соседние грузики, и в результате направо побежит впадина.
Если вместо продольных движений грузиков изучать их поперечные движения (в направлении оси у в плоскости ху), то графики рис. 5.3 изображают форму поперечного импульса в цепочке. Наблюдать такие импульсы и волны можно с помощью мягкой и достаточно длинной резиновой трубки. Проделать соответствующие простые опыты несложно, и читатель может проявить здесь фантазию и изобретательность.
В резиновой трубке или ленте, закрепленных на концах, легко возбуждать стоячие волны. Особенно легко возбуждается колебание, в котором нетрудно узнать «полусинусоиду». При этом все точки колеблются в одинаковой фазе, и амплитуда колебаний максимальна в середине («пучность» стоячей волны). Длина такой стоячей волны равна удвоенной длине ленты *). Труднее возбудить колебание, в котором остается в покое середина («узел» стоячей волны). На всей ленте при этом укладывается «период синусоиды», и длина волны равна длине ленты. Чтобы возбудить такое колебание, нужно оттянуть ленты в противоположные стороны на равных расстояниях от краев, удерживая середину в покое. Легче наблюдать такую волну на приборчике со скрепками. Возбудив какие-либо колебания в этой цепочке (лучше всего это делать быстрым, легким щелчком по скрепке), можно просто остановить среднюю скрепку. При этом «выживет» колебание, в котором средняя скрепка покоится.
*) Ниже мы увидим, что синусоидальную стоячую волну можно представить в виде суммы двух одинаковых волн, бегущих в противоположных направлениях. Длина стоячей волны, по определению, совпадает с длиной этих бегущих волн.
Стоячие волны разных типов, в которых на всей длине ленты укладывается разное число N полуволн, называются нормальными модами колебаний (или просто модами; это слово происходит от латинского modus, т. е. образ, способ). Моды с малыми значениями N называются низшими, а с большими — высшими. Моду с N = 1 естественно называть основной, она возбуждается легче всего. При произвольном начальном возбуждении нашей системы возбуждаются разные моды, однако высшие моды не только труднее возбуждаются, но и быстрее затухают из-за трения. Потому-то их и труднее наблюдать.
Понять, что такое моды и как они себя ведут, проще всего на модели одномерной цепочки конечной длины с закрепленными концами. Сначала посмотрим, как колеблется простейшая цепочка из двух атомов. Пусть их равновесные положения равны x01 = ? и x02 = 2?, а крайние пружинки закреплены в точках x00 = 0 и x03 = 3? (см. рис. 5.1). Легко составить уравнения движения атомов.
Прежде чем это сделать, введем одно небольшое новшество в обозначениях. До сих пор нам приходилось иметь дело лишь с производными по времени, и мы их обозначали штрихом. При изучении колебаний в распределенных системах встречаются не только производные по времени, с помощью которых записываются скорости и ускорения отдельных частичек, но и производные по координате. Они характеризуют изменение отклонения при переходе от одной частицы к другой в один и тот же момент времени. Поэтому условимся обозначать производную по времени не штрихом, а точкой, а штрих сохраним для производной по координате. Теперь мы будем обозначать скорость n-гo грузика как 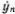 , а его ускорение — как
, а его ускорение — как 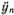 .
.
Уравнения движения грузиков можно тогда написать в виде
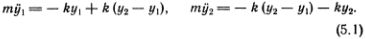
Действительно, сила, с которой левая пружина тянет первый грузик, равна произведению модуля упругости k на удлинение пружины y1, и при y1  0 эта сила направлена в отрицательном направлении оси х. Так получается член ky1 *). Удлинение правой пружины равно (y2 - y1), и она тянет грузик с силой k(y2 - y1). Это дает второй член в правой части первого уравнения. Точно так же находим силу, действующую на второй грузик.
0 эта сила направлена в отрицательном направлении оси х. Так получается член ky1 *). Удлинение правой пружины равно (y2 - y1), и она тянет грузик с силой k(y2 - y1). Это дает второй член в правой части первого уравнения. Точно так же находим силу, действующую на второй грузик.
*) Предполагается, что упругие свойства пружины соответствуют закону Гука. Нелинейность зависимости силы отклонения вводится с помощью других, дополнительных источников силы.
На первый взгляд может показаться, что решить эти уравнения очень сложно. Однако они линейны, а это значит, что достаточно найти лишь некоторый запас решений. Их линейные комбинации, возможно, и дадут самое общее решение.
Для начала попробуем получить хоть какие-нибудь решения. В этом нам поможет физическая интуиция. Действительно, вслед за Ньютоном мы представляем себе простейшую бегущую волну как процесс распространения гармонического колебания от одной частицы к другой. Тогда стоячая волна — это просто установившиеся колебания всех частичек с разными амплитудами. Сделаем простейшее предположение: допустим, что все частицы колеблются гармонически и притом с одинаковой частотой ?, и посмотрим, что отсюда следует.
Для гармонических колебаний ускорение пропорционально отклонению, т. е. 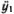 = -?2y1 и
= -?2y1 и 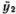 = -?2y2. Подставляя это в уравнения (5.1), получаем простую линейную систему уравнений для y1 и y2:
= -?2y2. Подставляя это в уравнения (5.1), получаем простую линейную систему уравнений для y1 и y2:
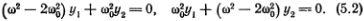
Здесь ?02 = k/m, а ? — не определенная пока частота наших гипотетических колебаний.
Ясно, что у этой системы уравнений относительно неизвестных y1 и y2 есть неинтересное решение y1 = y2 = 0. Пусть y1 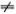 0. Тогда, выражения y2 через y1 из первого уравнения и подставляя полученное выражение во второе уравнение, найдем, что должно выполняться условие
0. Тогда, выражения y2 через y1 из первого уравнения и подставляя полученное выражение во второе уравнение, найдем, что должно выполняться условие
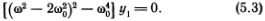
Так как y1 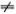 0, то выражение в квадратных скобках должно быть равно нулю *). Решая квадратное уравнение для ?2, определяем два возможных значения частоты
0, то выражение в квадратных скобках должно быть равно нулю *). Решая квадратное уравнение для ?2, определяем два возможных значения частоты
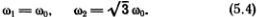
*) Если хотя бы в один момент времени y1 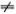 0, то множитель в квадратных скобках, не зависящий от времени, должен обращаться в нуль.
0, то множитель в квадратных скобках, не зависящий от времени, должен обращаться в нуль.
Если ? = ?1, то из уравнений (5.2) следует, что y2 = y1. Если ? = ?2, то y2 = -y1. Вспомним теперь, что y1 и y2 подчиняются уравнениям 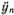 = -?2yn, которые определяют их гармоническую зависимость от времени. При ? = ?1 = ?0 можно поэтому записать решение в виде
= -?2yn, которые определяют их гармоническую зависимость от времени. При ? = ?1 = ?0 можно поэтому записать решение в виде
y1 = y2 = А1 cos [?1 (t - t1)], (5.5а)
а при ? = ?2 = 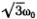 — в виде
— в виде
y1 = -y2 = А2 cos [?2 (t - t2)]. (5.5б)
Здесь A1 и А2 — произвольные амплитуды, а t1 и t2 — произвольные значения времени, определяющие фазу колебаний.
Эти два решения и дают две возможные моды колебаний нашей простейшей системы (рис. 5.4).
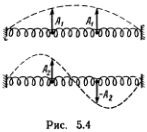
Они соответствуют двум нашим модам колебаний резинки, изображенным на рисунке штриховыми линиями. Конечно, это соответствие несколько условно, но, согласитесь, от карикатуры, сделанной двумя точками, нельзя требовать большего! Теперь можно снова воспользоваться линейностью уравнений (5.1) и написать решение в виде суммы решений (5.5а) и (5.5б):
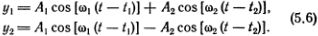
Это движение уже не сводится к простому гармоническому колебанию каждой из частиц. В общем случае, т. е. при произвольных значениях А1, А2, t1, t2, движение системы не будет даже периодическим.
Упражнение: рассмотрите простой случай, когда А1 = А2 = 1, t1 = t2 = 0, и покажите, что из-за несоизмеримости частот ?1 и ?2 не существует такого значения Т, при котором y1(Т) = y1(0), y2(Т) = y2(0). Это и означает, что такое движение не может быть периодическим.
Ясно, что формулы (5.6) дают самое общее движение. Начальное состояние определяется координатами и скоростями частиц, т. е. значениями y1(0), y2(0), 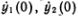 . Формулы (5.6) и их производные по времени позволяют найти неизвестные константы А1, А2, t1, t2 через начальные координаты и скорости.
. Формулы (5.6) и их производные по времени позволяют найти неизвестные константы А1, А2, t1, t2 через начальные координаты и скорости.
Замечательно, что нам удалось не только найти самое общее движение, но и разложить его на сумму самых простых из известных нам движений.
Конечно, в такой простой задаче то же самое можно было бы сделать и более простым способом. Например, если сложить и вычесть уравнения (5.1), то легко получить два независимых уравнения для (y1 + y2) и (y1 - y2), которые сразу решаются и приводят к формулам (5.6).
Однако наш чуть более длинный способ решения имеет преимущество — он легко обобщается на случай цепочки с любым числом частиц.
В качестве упражнения найдите частоты трех мод колебаний цепочки, состоящей из трех частиц. Для частот должен получиться результат: 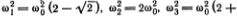
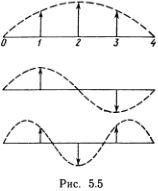
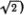 . Сами моды выглядят, как показано на рис. 5.5. Точный смысл этого рисунка (как и рис. 5.4) состоит в том, что моду с номером М можно представить в виде
. Сами моды выглядят, как показано на рис. 5.5. Точный смысл этого рисунка (как и рис. 5.4) состоит в том, что моду с номером М можно представить в виде
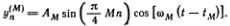
При заданном М = 1, 2, 3 индекс n пробегает три значения: n = 1, 2, 3, т. е. 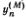 задает отклонение n-гo грузика в М-й моде. В случае двух частиц отклонения для двух мод можно написать в аналогичном виде
задает отклонение n-гo грузика в М-й моде. В случае двух частиц отклонения для двух мод можно написать в аналогичном виде
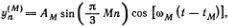
где М = 1, 2 и n = 1, 2.
Общую закономерность теперь нетрудно уловить и она наглядно ясна — нарисованные штрихами синусоиды соответствуют стоячим волнам. Легко также догадаться, что в цепочке из N частиц моду с номером М надо искать в виде
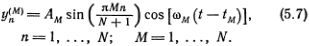
Уравнение движения для n-гo атома составляется точно так же, как уравнения (5.1), т. е.
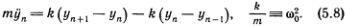
Это уравнение годится и для крайних атомов — первого и N-гo. Нужно только вспомнить, что крайние пружинки закреплены, т. е. у0 = yN+1 = 0. Эти условия для предполагаемых решений (5.7) уже выполнены. Теперь должно быть ясно, как довести решение до конца. Надо подставить выражение (5.7) в уравнение (5.8) и заменить 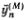 на -?2Myn(М). После несложных преобразований тригонометрических функций получится соотношение для ?2M, при выполнении которого все уравнения (5.8) удовлетворяются; это выражение мы приведем без вывода
на -?2Myn(М). После несложных преобразований тригонометрических функций получится соотношение для ?2M, при выполнении которого все уравнения (5.8) удовлетворяются; это выражение мы приведем без вывода
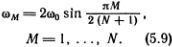
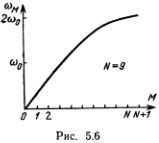
Эта зависимость частоты от номера моды изображена на рис. 5.6. Для мод с малыми номерами (низкочастотных и длинноволновых) частота пропорциональна номеру моды. Для высокочастотных мод (коротковолновых) частота выходит на предельное значение 2?0.
Формула (5.9) определяет спектр частот собственных колебаний (мод) цепочки. Не удивительно, что в цепочке из N частиц имеется ровно N собственных частот. Нетрудно понять и происхождение предельной частоты. Если один из грузиков колеблется слишком быстро, то соседние не успевают реагировать на его движение, и возбуждение не сможет распространяться вдоль цепочки. Этот вывод легко проверить, проделав простые опыты.
Читателю стоит потратить некоторое время, чтобы самостоятельно разобраться в этих результатах. Затраченные усилия полностью окупаются. После уравнений Галилея — Ньютона и принципа сохранения энергии разложение произвольного движения на моды, или нормальные колебания, представляет собой, возможно, самой фундаментальный результат физики. Его обобщения и приложения, от простых механических задач до современных проблем физики элементарных частиц, просто невозможно перечислить.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК